2.6.2 有理数的乘法与除法 课件(21张PPT)
文档属性
| 名称 | 2.6.2 有理数的乘法与除法 课件(21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 54.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-22 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
2.6.2 有理数的乘法
与除法
第2章有理数
教学目标
01
理解有理数的除法法则
02
能灵活运用有理数的除法法则进行运算
有理数的除法
01
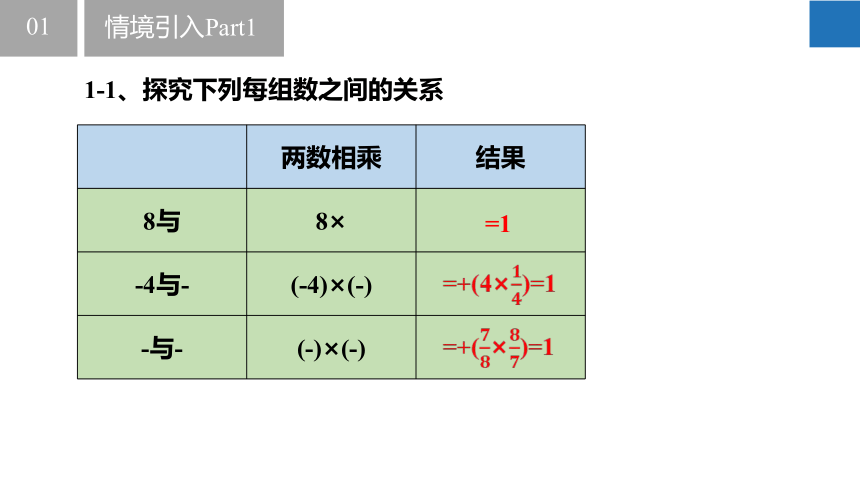
1-1、探究下列每组数之间的关系
情境引入Part1
两数相乘 结果
8与 8×
-4与- (-4)×(-)
-与- (-)×(-)
=1
=+(4×)=1
=+(×)=1
像8与、-4与-、-与-……这样乘积为1的两个数互为倒数,其中一个数叫做另一个数的倒数。
注意:0没有倒数!
倒数
01
情境引入Part1
倒数
1-2、完成下列填空:
(1)2的倒数是_______,的倒数是_______;
(2)-2的倒数是_______,-的倒数是_______;
(3)一个数的倒数是它本身的数是_______;
(4)正数的倒数是______,负数的倒数是_______。
2
-
-
±1
01
情境引入Part1
正数
负数
倒数
01
情境引入Part1
倒数
求一个数的倒数的方法 求一个整数的倒数,就是写成这个整数分之一
求一个分数的倒数,就是调换分子和分母的位置
2、下面是张红一周的结余情况表(单位为元)
周一 周二 周三 周四 周五 周六 周日
-7 +2 10 -13 -6 -2 -5
问:张红平均每天的结余为?
答:[(-7)+2+10+(-13)+(-6)+(-2)+(-5)]÷7,即(-21)÷7(元)
01
情境引入Part2
如何计算(-21)÷7?
求(-21)÷7,就是要求一个数,使它与7的积是(-21),这个数是-3
(-21)×=-3
∵(-3)×7=-21
∴(-21)÷7=-3
01
情境引入Part2
求(-21)÷7,小学里我们学过,除以一个数等于乘这个数的倒数
除号变乘号
(-21)÷7=-3
(-21)×=-3
01
情境引入
7变成它的倒数
乘以7的倒数
01
4、参照(-21)÷7=(-21)×,填空:
(1) (-10)÷2=(-10)×_______;
(2) 24÷(-8)=24×_______;
(3) (-12)÷(-4)=(-12)×_______.
情境引入
乘以2的倒数
乘以-8的倒数
-
乘以-4的倒数
-
02
除法法则
知识精讲
有理数的除法法则:
除以一个不等于0的数,等于乘以这个数的倒数
解:(1)原式=0×(-)=0
例1、计算:(1)0÷(-)
(2)24÷(-3)÷4
(2)原式=24×(-)×=-(24××)=-
03
典例精析
0除以任何一个不等于0的数,
都得0
解:(3)原式=11÷(-)÷5=11×(-)×=-(11××)=-1
例1、计算:(3)11÷(-2)÷5
(4)(+1)÷(-)÷(-)÷(-)
(4)原式=÷(-)÷(-)÷(-)=×(-)×(-)×(-)=-(×××)=-1
03
典例精析
解:原式
=(1-+-+-)×(-60)
=1×(-60)+(-)×(-60)+×(-60)+(-)×(-60)+×(-60)+(-)×(-60)
=(-60)+30+(-20)+15+(-12)+10
=-37
例2、计算:(1-+-+-)÷(-)
03
典例精析
【法一】解:(1)原式=÷=÷=×6=
例3、计算:(1)÷(-+)
03
典例精析
【法二】解:(1)原式的倒数=(-+)÷
=(-+)×24=×24+(-)×24+×24=8+(-6)+2=4
∴原式=
【法一】解:(2)原式=(-)÷=(-)÷=(-)×3=-
例3、计算:(2)(-)÷(-+-)
03
典例精析
【法二】解:(2)原式的倒数=(-+-)÷(-)
=(-+-)×(-42)=×(-42)+(-)×(-42)+×(-42)+(-)×(-42)
=-7+9+(-28)+12=-14
∴原式=-
解:(1)原式=×(-)×(-5)×5=+(××5×5)=1
例4、混合计算:(1) ÷(-5)÷(-)×5
(2) 2÷(-)×÷(-5)
03
典例精析
(2)原式=2÷(-)×÷(-)=2×(-)××(-)=+(2×××)=
解:(3)原式=÷(-)×(-)÷(-)
=×(-)×(-)×(-)
=-(×××)
=-
例4、混合计算:(3) (+5)÷(-4)×(-)÷(-3)
03
典例精析
解:(4)原式=(-)×(-3)÷×(-2)
=(-)×(-3)××(-2)
=-(×3××2)
=-
例4、混合计算:(4)(-)×(-3)÷|-1|×(-2)
03
典例精析
有绝对值先算绝对值
课后总结
有理数的除法法则:
除以一个不等于0的数,等于乘以这个数的倒数
0除以任何一个不等于0的数,都得0
乘积为1的两个数互为倒数,其中一个数叫做另一个数的倒数。
注意:0没有倒数!
2.6.2 有理数的乘法
与除法
第2章有理数
教学目标
01
理解有理数的除法法则
02
能灵活运用有理数的除法法则进行运算
有理数的除法
01
1-1、探究下列每组数之间的关系
情境引入Part1
两数相乘 结果
8与 8×
-4与- (-4)×(-)
-与- (-)×(-)
=1
=+(4×)=1
=+(×)=1
像8与、-4与-、-与-……这样乘积为1的两个数互为倒数,其中一个数叫做另一个数的倒数。
注意:0没有倒数!
倒数
01
情境引入Part1
倒数
1-2、完成下列填空:
(1)2的倒数是_______,的倒数是_______;
(2)-2的倒数是_______,-的倒数是_______;
(3)一个数的倒数是它本身的数是_______;
(4)正数的倒数是______,负数的倒数是_______。
2
-
-
±1
01
情境引入Part1
正数
负数
倒数
01
情境引入Part1
倒数
求一个数的倒数的方法 求一个整数的倒数,就是写成这个整数分之一
求一个分数的倒数,就是调换分子和分母的位置
2、下面是张红一周的结余情况表(单位为元)
周一 周二 周三 周四 周五 周六 周日
-7 +2 10 -13 -6 -2 -5
问:张红平均每天的结余为?
答:[(-7)+2+10+(-13)+(-6)+(-2)+(-5)]÷7,即(-21)÷7(元)
01
情境引入Part2
如何计算(-21)÷7?
求(-21)÷7,就是要求一个数,使它与7的积是(-21),这个数是-3
(-21)×=-3
∵(-3)×7=-21
∴(-21)÷7=-3
01
情境引入Part2
求(-21)÷7,小学里我们学过,除以一个数等于乘这个数的倒数
除号变乘号
(-21)÷7=-3
(-21)×=-3
01
情境引入
7变成它的倒数
乘以7的倒数
01
4、参照(-21)÷7=(-21)×,填空:
(1) (-10)÷2=(-10)×_______;
(2) 24÷(-8)=24×_______;
(3) (-12)÷(-4)=(-12)×_______.
情境引入
乘以2的倒数
乘以-8的倒数
-
乘以-4的倒数
-
02
除法法则
知识精讲
有理数的除法法则:
除以一个不等于0的数,等于乘以这个数的倒数
解:(1)原式=0×(-)=0
例1、计算:(1)0÷(-)
(2)24÷(-3)÷4
(2)原式=24×(-)×=-(24××)=-
03
典例精析
0除以任何一个不等于0的数,
都得0
解:(3)原式=11÷(-)÷5=11×(-)×=-(11××)=-1
例1、计算:(3)11÷(-2)÷5
(4)(+1)÷(-)÷(-)÷(-)
(4)原式=÷(-)÷(-)÷(-)=×(-)×(-)×(-)=-(×××)=-1
03
典例精析
解:原式
=(1-+-+-)×(-60)
=1×(-60)+(-)×(-60)+×(-60)+(-)×(-60)+×(-60)+(-)×(-60)
=(-60)+30+(-20)+15+(-12)+10
=-37
例2、计算:(1-+-+-)÷(-)
03
典例精析
【法一】解:(1)原式=÷=÷=×6=
例3、计算:(1)÷(-+)
03
典例精析
【法二】解:(1)原式的倒数=(-+)÷
=(-+)×24=×24+(-)×24+×24=8+(-6)+2=4
∴原式=
【法一】解:(2)原式=(-)÷=(-)÷=(-)×3=-
例3、计算:(2)(-)÷(-+-)
03
典例精析
【法二】解:(2)原式的倒数=(-+-)÷(-)
=(-+-)×(-42)=×(-42)+(-)×(-42)+×(-42)+(-)×(-42)
=-7+9+(-28)+12=-14
∴原式=-
解:(1)原式=×(-)×(-5)×5=+(××5×5)=1
例4、混合计算:(1) ÷(-5)÷(-)×5
(2) 2÷(-)×÷(-5)
03
典例精析
(2)原式=2÷(-)×÷(-)=2×(-)××(-)=+(2×××)=
解:(3)原式=÷(-)×(-)÷(-)
=×(-)×(-)×(-)
=-(×××)
=-
例4、混合计算:(3) (+5)÷(-4)×(-)÷(-3)
03
典例精析
解:(4)原式=(-)×(-3)÷×(-2)
=(-)×(-3)××(-2)
=-(×3××2)
=-
例4、混合计算:(4)(-)×(-3)÷|-1|×(-2)
03
典例精析
有绝对值先算绝对值
课后总结
有理数的除法法则:
除以一个不等于0的数,等于乘以这个数的倒数
0除以任何一个不等于0的数,都得0
乘积为1的两个数互为倒数,其中一个数叫做另一个数的倒数。
注意:0没有倒数!
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
