人教版数学八年级上册 13.3.1.1 等腰三角形的性质课件 (共18张PPT)
文档属性
| 名称 | 人教版数学八年级上册 13.3.1.1 等腰三角形的性质课件 (共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-23 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
13.3.1.1 等腰三角形的性质
1.理解并掌握等腰三角形的性质.
2.经历等腰三角形的性质的探究过程,能初步运用等腰三角形的性质解决有关问题.
学 习 目 标
叫做
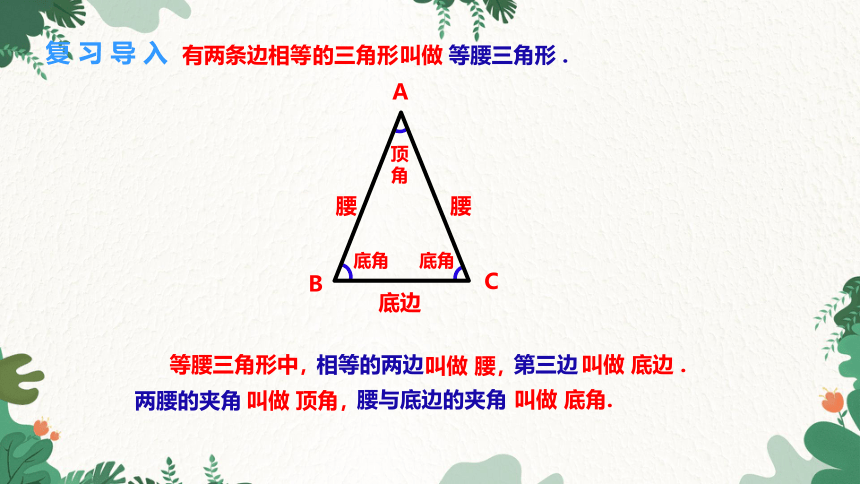
有两条边相等
的三角形
等腰三角形 .
等腰三角形中,
相等的两边
叫做 腰,
腰
腰
底边
底角
底角
顶
角
第三边
叫做 底边 .
两腰的夹角
叫做 顶角,
腰与底边的夹角
叫做 底角.
A
B
C
复 习 导 入
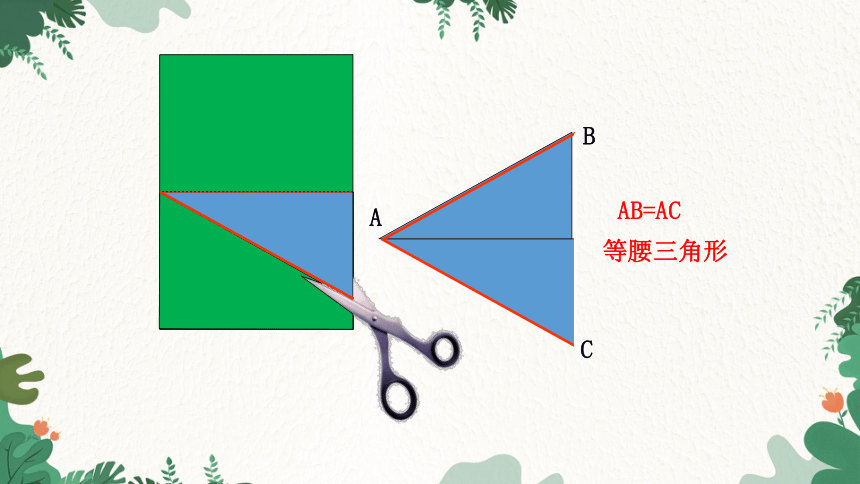
剪一剪:把一张长方形的纸按
图中的红线对折,并剪去阴影
部分(一个直角三角形),再
把得到的直角三角形展开,得
到的三角形ABC有什么特点?
合 作 探 究
A
B
C
AB=AC
等腰三角形
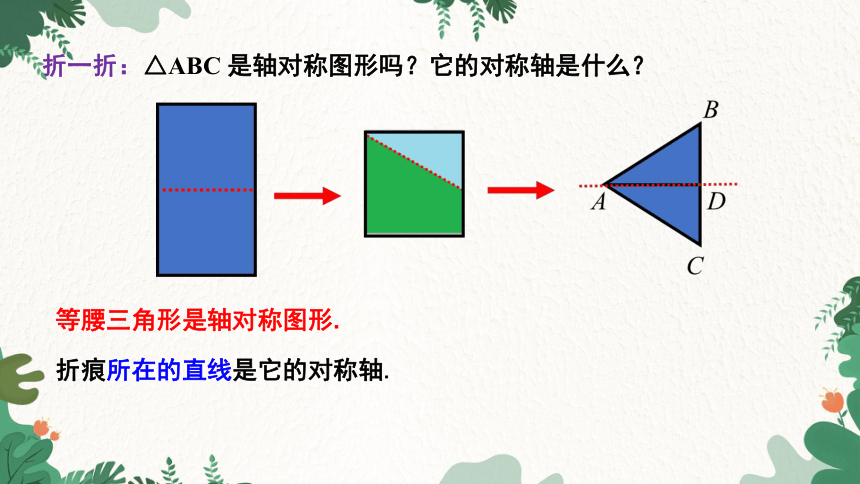
折一折:△ABC 是轴对称图形吗?它的对称轴是什么?
折痕所在的直线是它的对称轴.
等腰三角形是轴对称图形.
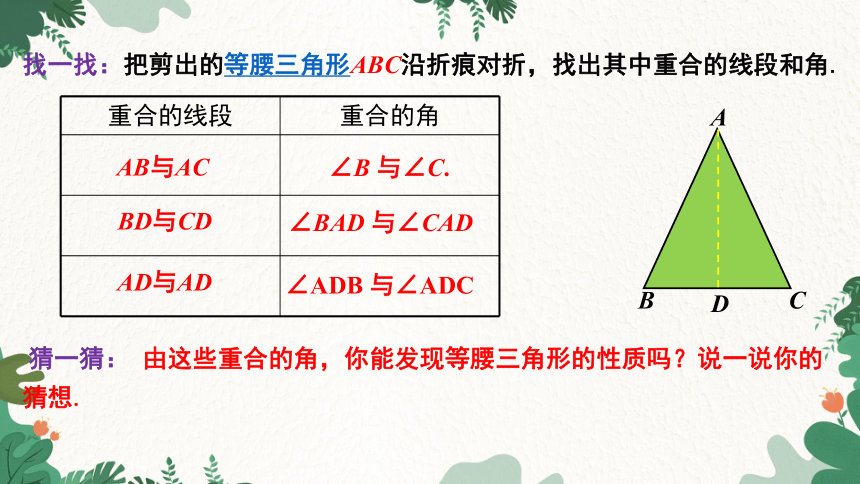
找一找:把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角.
重合的线段 重合的角
A
C
B
D
AB与AC
BD与CD
AD与AD
∠B 与∠C.
∠BAD 与∠CAD
∠ADB 与∠ADC
猜一猜: 由这些重合的角,你能发现等腰三角形的性质吗?说一说你的猜想.
猜想:等腰三角形的两个底角相等
已知:△ABC中,AB=AC,
求证:∠B=∠C.
思考:如何构造两个全等的三角形?
猜想:等腰三角形的两个底角相等
如何证明两个角相等呢?
可以运用全等三角形的性质“对应角相等”来证
已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
D
证明:
作底边的中线AD,则BD=CD.
AB=AC ( 已知 ),
BD=CD ( 已作 ),
AD=AD (公共边),
∴ △BAD≌ △CAD (SSS).
∴ ∠B= ∠C (全等三角形的对应角相等).
在△BAD和△CAD中
方法一:作底边上的中线
还有其他的证法吗?
已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
D
证明:
作顶角的平分线AD,则∠BAD=∠CAD.
AB=AC ( 已知 ),
∠BAD=∠CAD ( 已作 ),
AD=AD (公共边),
∴ △BAD ≌ △CAD (SAS).
∴ ∠B= ∠C (全等三角形的对应角相等).
方法二:作顶角的平分线
在△BAD和△CAD中
思考:由△BAD≌ △CAD,除了可以得到∠B= ∠C之外,你还可以得到那些相等的线段和相等的角?和你的同伴交流一下,看看你有什么新的发现?
解:∵△BAD≌ △CAD,由全等三角形的性质易得BD=CD,∠ADB=∠ADC,∠BAD=∠CAD.
又∵ ∠ADB+∠ADC=180°,
∴ ∠ADB=∠ADC= 90° ,
即AD是等腰△ABC底边BC上的中线、顶角∠BAC的角平分线、底边BC上的高线 .
A
B
C
D
等腰三角形的性质
A
B
C
定理 1:
等腰三角形的两个底角相等。
简称“等边对等角”
几何语言:
∵ 在△ABC中,AB=AC
∴ ∠B=∠C
(等边对等角)
定理 2:
顶角平分线、
互相重合.
底边上的中线、
底边上的高
等腰三角形的
简称“三线合一”
等腰三角形
垂直平分底边
顶角的平分线
即
思考: 在等腰三角形中,若出现“三线”中的“一线”,我们应该想到什么?
知一得二
A
B
C
D
新 知 小 结
已知:如图,在△ABC 中,AB=AC,∠BAC=120 ,点 D ,E 是底边上两点,且 BD=AD,CE=AE。求∠DAE 的度数。
A
B
C
D
E
∵ AB=AC
∴ ∠B=∠C
(已知)
(等边对等角)
∴ ∠B=∠C
= ×(180°-120°)
1
2
=30°
∵ BD=AD,CE=AE
(已知)
∴ ∠BAD=∠B=30°
∠CAE=∠C=30°
(等边对等角)
∴ ∠DAE=
=120°-30°-30°
=60°
∠BAC
-∠BAD
-∠CAE
解:
典 例 精 析
1.等腰三角形的顶角一定是锐角.
2.等腰三角形的底角可能是锐角或者直角、钝角都可以.
3.钝角三角形不可能是等腰三角形.
4.等腰三角形的顶角平分线一定垂直底边.
5.等腰三角形的角平分线、中线和高互相重合.
6.等腰三角形底边上的中线一定平分顶角.
( )
X
( )
( )
X
X
X
√
√
( )
( )
( )
随 堂 练 习
8.如图,在△ABC中,AB=AC,过点A作AD∥BC,若∠1=70°,则∠BAC的大小为( )
A.40° B.30° C.70° D.50°
A
7.等腰三角形有一个角是90°,则另两个角分别是( )
A.30°,60° B.45°,45°
C.45°,90° D.20°,70°
B
9.如图,在△ABC中,AB = AC,D是BC边上的中点, ∠B = 30°,求 ∠BAD 和 ∠ADC的度数.
A
B
C
D
解:∵AB=AC,D是BC边上的中点,
∴ ∠C= ∠ B=30°,
∠BAD = ∠ DAC,∠ADC = 90°.
∴∠ BAC =180° - 30°-30° = 120°.
∴ = 60°.
课 堂 总 结
谢谢大家!
13.3.1.1 等腰三角形的性质
1.理解并掌握等腰三角形的性质.
2.经历等腰三角形的性质的探究过程,能初步运用等腰三角形的性质解决有关问题.
学 习 目 标
叫做
有两条边相等
的三角形
等腰三角形 .
等腰三角形中,
相等的两边
叫做 腰,
腰
腰
底边
底角
底角
顶
角
第三边
叫做 底边 .
两腰的夹角
叫做 顶角,
腰与底边的夹角
叫做 底角.
A
B
C
复 习 导 入
剪一剪:把一张长方形的纸按
图中的红线对折,并剪去阴影
部分(一个直角三角形),再
把得到的直角三角形展开,得
到的三角形ABC有什么特点?
合 作 探 究
A
B
C
AB=AC
等腰三角形
折一折:△ABC 是轴对称图形吗?它的对称轴是什么?
折痕所在的直线是它的对称轴.
等腰三角形是轴对称图形.
找一找:把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角.
重合的线段 重合的角
A
C
B
D
AB与AC
BD与CD
AD与AD
∠B 与∠C.
∠BAD 与∠CAD
∠ADB 与∠ADC
猜一猜: 由这些重合的角,你能发现等腰三角形的性质吗?说一说你的猜想.
猜想:等腰三角形的两个底角相等
已知:△ABC中,AB=AC,
求证:∠B=∠C.
思考:如何构造两个全等的三角形?
猜想:等腰三角形的两个底角相等
如何证明两个角相等呢?
可以运用全等三角形的性质“对应角相等”来证
已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
D
证明:
作底边的中线AD,则BD=CD.
AB=AC ( 已知 ),
BD=CD ( 已作 ),
AD=AD (公共边),
∴ △BAD≌ △CAD (SSS).
∴ ∠B= ∠C (全等三角形的对应角相等).
在△BAD和△CAD中
方法一:作底边上的中线
还有其他的证法吗?
已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
D
证明:
作顶角的平分线AD,则∠BAD=∠CAD.
AB=AC ( 已知 ),
∠BAD=∠CAD ( 已作 ),
AD=AD (公共边),
∴ △BAD ≌ △CAD (SAS).
∴ ∠B= ∠C (全等三角形的对应角相等).
方法二:作顶角的平分线
在△BAD和△CAD中
思考:由△BAD≌ △CAD,除了可以得到∠B= ∠C之外,你还可以得到那些相等的线段和相等的角?和你的同伴交流一下,看看你有什么新的发现?
解:∵△BAD≌ △CAD,由全等三角形的性质易得BD=CD,∠ADB=∠ADC,∠BAD=∠CAD.
又∵ ∠ADB+∠ADC=180°,
∴ ∠ADB=∠ADC= 90° ,
即AD是等腰△ABC底边BC上的中线、顶角∠BAC的角平分线、底边BC上的高线 .
A
B
C
D
等腰三角形的性质
A
B
C
定理 1:
等腰三角形的两个底角相等。
简称“等边对等角”
几何语言:
∵ 在△ABC中,AB=AC
∴ ∠B=∠C
(等边对等角)
定理 2:
顶角平分线、
互相重合.
底边上的中线、
底边上的高
等腰三角形的
简称“三线合一”
等腰三角形
垂直平分底边
顶角的平分线
即
思考: 在等腰三角形中,若出现“三线”中的“一线”,我们应该想到什么?
知一得二
A
B
C
D
新 知 小 结
已知:如图,在△ABC 中,AB=AC,∠BAC=120 ,点 D ,E 是底边上两点,且 BD=AD,CE=AE。求∠DAE 的度数。
A
B
C
D
E
∵ AB=AC
∴ ∠B=∠C
(已知)
(等边对等角)
∴ ∠B=∠C
= ×(180°-120°)
1
2
=30°
∵ BD=AD,CE=AE
(已知)
∴ ∠BAD=∠B=30°
∠CAE=∠C=30°
(等边对等角)
∴ ∠DAE=
=120°-30°-30°
=60°
∠BAC
-∠BAD
-∠CAE
解:
典 例 精 析
1.等腰三角形的顶角一定是锐角.
2.等腰三角形的底角可能是锐角或者直角、钝角都可以.
3.钝角三角形不可能是等腰三角形.
4.等腰三角形的顶角平分线一定垂直底边.
5.等腰三角形的角平分线、中线和高互相重合.
6.等腰三角形底边上的中线一定平分顶角.
( )
X
( )
( )
X
X
X
√
√
( )
( )
( )
随 堂 练 习
8.如图,在△ABC中,AB=AC,过点A作AD∥BC,若∠1=70°,则∠BAC的大小为( )
A.40° B.30° C.70° D.50°
A
7.等腰三角形有一个角是90°,则另两个角分别是( )
A.30°,60° B.45°,45°
C.45°,90° D.20°,70°
B
9.如图,在△ABC中,AB = AC,D是BC边上的中点, ∠B = 30°,求 ∠BAD 和 ∠ADC的度数.
A
B
C
D
解:∵AB=AC,D是BC边上的中点,
∴ ∠C= ∠ B=30°,
∠BAD = ∠ DAC,∠ADC = 90°.
∴∠ BAC =180° - 30°-30° = 120°.
∴ = 60°.
课 堂 总 结
谢谢大家!
