初中数学人教版七下6.1平方根(第1课时)—算术平方根 课件(共23张PPT)
文档属性
| 名称 | 初中数学人教版七下6.1平方根(第1课时)—算术平方根 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-22 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
6.1 平方根(1)
第六章 实数
算术平方根
神舟十三号载人飞船
本章导入
本章导入
你们知道宇宙飞船离开地球进入轨道正常运行的速度在什么范围内吗
你们知道宇宙飞船离开地球进入轨道正常运行的速度在什么范围内吗
阅读本章前言
要解决上面问题,我们需要引入一种新的数——无理数.
本章将首先学习平方根与立方根;在此基础上引入无理数,把数的范围扩充到实数;然后类比有理数,引入实数在数轴上的表示和实数的运算,并用这些知识解决一些实际问题.
本章导入
6.1 平方根(1)
算术平方根
新课导入
学校要举行美术作品比赛,小鸥想裁出一块面积为 25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少
25 dm2
因为 52 = 25,所以这个正方形的边长应取 5 dm.
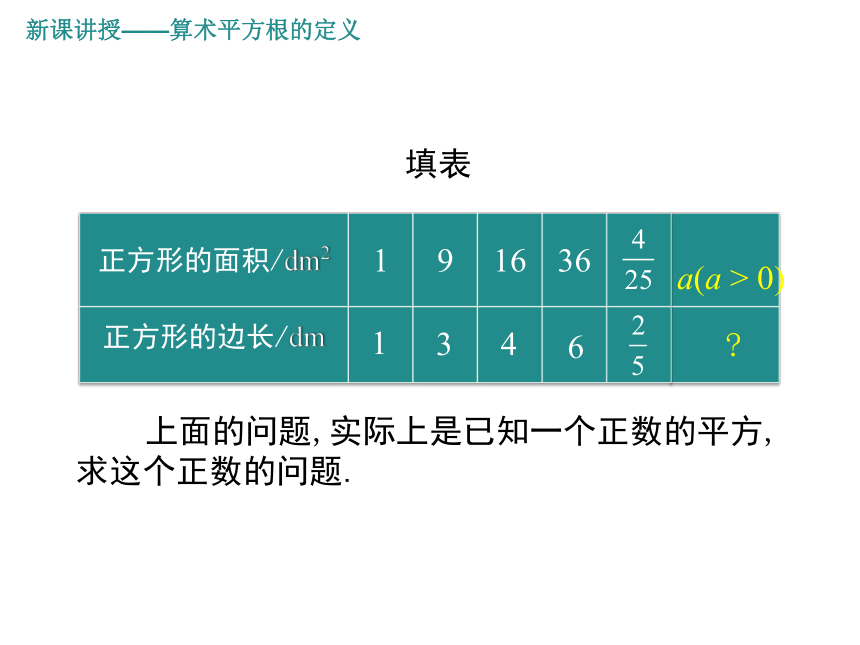
正方形的面积/dm2 1 9 16 36
正方形的边长/dm
填表
1
3
4
6
上面的问题,实际上是已知一个正数的平方,求这个正数的问题.
a(a > 0)
新课讲授——算术平方根的定义
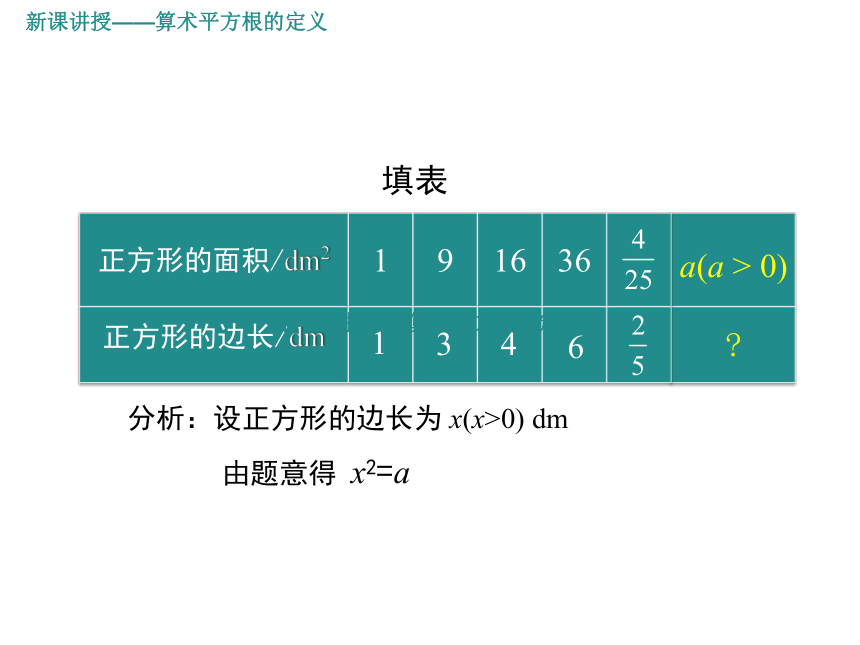
分析:设正方形的边长为 x(x>0) dm
正方形的面积/dm2 1 9 16 36
正方形的边长/dm
填表
1
3
4
6
由题意得 x2=a
a(a > 0)
新课讲授——算术平方根的定义
新课讲授——算术平方根的定义
如:32 = 9 ,所以 9 的算术平方根是 3;即 .
一般地,如果一个正数 x 的平方等于 a ,即 x2 = a,那么这个正数 x 叫做 a 的算术平方根. a 的算术平方根记为 ,读作“根号 a”, a 叫做被开方数.
规定:0 的算术平方根是 0.
算术平方根的定义
新课讲授——算术平方根的定义
例1 求下列各数的算术平方根:
(1)100 (2) (3)0.0001
解:(1)因为 =100,所以100的算术平方根为10,即 =10.
(2)因为 = ,所以 的算术平方根是 ,即 =
(3)因为 =0.0001,所以0.0001的算术平方根为0.01,即
=0.01.
从例1可以看出:被开方数越大,对应的算术平方根也越大,这个结论对所有正数都成立.
典型例题
1. 81的算术平方根是 ;
0.0025的算术平方根是 ;
0 的算术平方根是 ;
的算术平方根是 ;
32的算术平方根是 ;
9
0
课堂练习
= ___________.
的算术平方根等于_________.
2
16的算术平方根是_________.
4
4
16
16
2.
课堂练习
如图,把两个小正方形分别沿对角线剪开,将所得的4个直角三角形拼在一起,就得到一个面积为2dm 的大正方形.你知道这个大正方形的边长是多少吗?
新课讲授——
设大正方形的边长为 x dm,则x =2.
由算术平方根的意义可知
所以大正方形的边长是 dm
小正方形的对角线的长是多少呢?
小正方形的对角线和大正方形的
边长有什么关系吗?
新课讲授——
有多大呢?
根据算术平方根随着被开方数的变大而变大,可以估计
大于1小于2
因为 1 = 1,2 = 4,
所以 1 < < 2;
因为 1.4 = 1.96,1.5 = 2.25,
所以 1.4 < < 1.5;
因为 1.41 = 1.9881,1.42 = 2.0164,
所以 1.41 < < 1.42;
因为 1.414 = 1.999396,1.415 = 2.002225,
所以 1.414 < < 1.415;……
随着估计范围的收窄,
数据在逐渐的逼近
新课讲授——
事实上,继续重复上述的过程,可以得到
它是一个无限不循环小数
小数位数无限,
且小数部分不循环
新课讲授——
新课讲授——
(1)利用计算器(手机)计算下表中的算术平方根,并将计算结果填在表中,你发现了什么规律 你能说出其中的道理吗
... ...
... ...
0.25
0.7906
2.5
7.906
25
79.06
250
规律:被开方数的小数点向右(或向左)每移动 位,它的算术平方根的小数点就向右移动 位;
2
1
新课讲授——计算器与找规律
(2)用计算器计算 (精确到0.001),并利用你在(1)中发现的规律说出 的近似值,你能根据 的值说出 是多少吗
左2
左1
右2
右1
右2
右1
新课讲授——计算器与找规律
例3 小丽想用一块面积为 400 cm2
的正方形纸片,沿着边的方向裁
出一块面积为 300 cm2的长方形纸
片,使它的长宽之比为 3: 2. 她不
知能否裁得出来,正在发愁.
小明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?
典型例题
解:设长方形纸片的长为3x cm,宽为2x cm.
根据边长与面积的关系得
3x 2x=300,6x2 =300, x2 =50, x = .
因此长方形纸片的长为 cm.
因为50>49,所以 >7.
由上可知 >21,即长方形纸片的长应该大于21 cm.
因为 =20,所以正方形纸片的边长只有20cm. 这样,长方形纸片的长将大于正方形纸片的边长.
答:不能同意小明的说法.小丽不能用这块正方形纸片裁出符合要求的长方形纸片.
典型例题
课堂小结
一般地,如果一个正数 x 的平方等于 a ,即 x2 = a,那么这个正数 x 叫做 a 的算术平方根. a 的算术平方根记为 ,读作“根号 a”, a 叫做被开方数.
规定: 0 的算术平方根是 0.
依据算术平方根的定义,可求得某一个非负数的算术平方根.
研究
计算器
找规律
作业布置
1.解决章前言的问题.
2.完成配套作业
6.1 平方根(1)
第六章 实数
算术平方根
神舟十三号载人飞船
本章导入
本章导入
你们知道宇宙飞船离开地球进入轨道正常运行的速度在什么范围内吗
你们知道宇宙飞船离开地球进入轨道正常运行的速度在什么范围内吗
阅读本章前言
要解决上面问题,我们需要引入一种新的数——无理数.
本章将首先学习平方根与立方根;在此基础上引入无理数,把数的范围扩充到实数;然后类比有理数,引入实数在数轴上的表示和实数的运算,并用这些知识解决一些实际问题.
本章导入
6.1 平方根(1)
算术平方根
新课导入
学校要举行美术作品比赛,小鸥想裁出一块面积为 25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少
25 dm2
因为 52 = 25,所以这个正方形的边长应取 5 dm.
正方形的面积/dm2 1 9 16 36
正方形的边长/dm
填表
1
3
4
6
上面的问题,实际上是已知一个正数的平方,求这个正数的问题.
a(a > 0)
新课讲授——算术平方根的定义
分析:设正方形的边长为 x(x>0) dm
正方形的面积/dm2 1 9 16 36
正方形的边长/dm
填表
1
3
4
6
由题意得 x2=a
a(a > 0)
新课讲授——算术平方根的定义
新课讲授——算术平方根的定义
如:32 = 9 ,所以 9 的算术平方根是 3;即 .
一般地,如果一个正数 x 的平方等于 a ,即 x2 = a,那么这个正数 x 叫做 a 的算术平方根. a 的算术平方根记为 ,读作“根号 a”, a 叫做被开方数.
规定:0 的算术平方根是 0.
算术平方根的定义
新课讲授——算术平方根的定义
例1 求下列各数的算术平方根:
(1)100 (2) (3)0.0001
解:(1)因为 =100,所以100的算术平方根为10,即 =10.
(2)因为 = ,所以 的算术平方根是 ,即 =
(3)因为 =0.0001,所以0.0001的算术平方根为0.01,即
=0.01.
从例1可以看出:被开方数越大,对应的算术平方根也越大,这个结论对所有正数都成立.
典型例题
1. 81的算术平方根是 ;
0.0025的算术平方根是 ;
0 的算术平方根是 ;
的算术平方根是 ;
32的算术平方根是 ;
9
0
课堂练习
= ___________.
的算术平方根等于_________.
2
16的算术平方根是_________.
4
4
16
16
2.
课堂练习
如图,把两个小正方形分别沿对角线剪开,将所得的4个直角三角形拼在一起,就得到一个面积为2dm 的大正方形.你知道这个大正方形的边长是多少吗?
新课讲授——
设大正方形的边长为 x dm,则x =2.
由算术平方根的意义可知
所以大正方形的边长是 dm
小正方形的对角线的长是多少呢?
小正方形的对角线和大正方形的
边长有什么关系吗?
新课讲授——
有多大呢?
根据算术平方根随着被开方数的变大而变大,可以估计
大于1小于2
因为 1 = 1,2 = 4,
所以 1 < < 2;
因为 1.4 = 1.96,1.5 = 2.25,
所以 1.4 < < 1.5;
因为 1.41 = 1.9881,1.42 = 2.0164,
所以 1.41 < < 1.42;
因为 1.414 = 1.999396,1.415 = 2.002225,
所以 1.414 < < 1.415;……
随着估计范围的收窄,
数据在逐渐的逼近
新课讲授——
事实上,继续重复上述的过程,可以得到
它是一个无限不循环小数
小数位数无限,
且小数部分不循环
新课讲授——
新课讲授——
(1)利用计算器(手机)计算下表中的算术平方根,并将计算结果填在表中,你发现了什么规律 你能说出其中的道理吗
... ...
... ...
0.25
0.7906
2.5
7.906
25
79.06
250
规律:被开方数的小数点向右(或向左)每移动 位,它的算术平方根的小数点就向右移动 位;
2
1
新课讲授——计算器与找规律
(2)用计算器计算 (精确到0.001),并利用你在(1)中发现的规律说出 的近似值,你能根据 的值说出 是多少吗
左2
左1
右2
右1
右2
右1
新课讲授——计算器与找规律
例3 小丽想用一块面积为 400 cm2
的正方形纸片,沿着边的方向裁
出一块面积为 300 cm2的长方形纸
片,使它的长宽之比为 3: 2. 她不
知能否裁得出来,正在发愁.
小明见了说:“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片.”你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?
典型例题
解:设长方形纸片的长为3x cm,宽为2x cm.
根据边长与面积的关系得
3x 2x=300,6x2 =300, x2 =50, x = .
因此长方形纸片的长为 cm.
因为50>49,所以 >7.
由上可知 >21,即长方形纸片的长应该大于21 cm.
因为 =20,所以正方形纸片的边长只有20cm. 这样,长方形纸片的长将大于正方形纸片的边长.
答:不能同意小明的说法.小丽不能用这块正方形纸片裁出符合要求的长方形纸片.
典型例题
课堂小结
一般地,如果一个正数 x 的平方等于 a ,即 x2 = a,那么这个正数 x 叫做 a 的算术平方根. a 的算术平方根记为 ,读作“根号 a”, a 叫做被开方数.
规定: 0 的算术平方根是 0.
依据算术平方根的定义,可求得某一个非负数的算术平方根.
研究
计算器
找规律
作业布置
1.解决章前言的问题.
2.完成配套作业
