初中数学人教版七下6.2立方根 课件(共24张PPT)
文档属性
| 名称 | 初中数学人教版七下6.2立方根 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 14.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-22 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
第六章 实 数
6.2 立方根
学习目标
1.理解立方根的概念,会用根号表示一个数的立方根.会求一个数的立方根,了解开立方与立方互为逆运算.
2.掌握立方根的性质,能区分立方根与平方根的不同.通过类比平方根学习立方根,体会类比思想的运用.
3.会用计算器计算一个数的立方根或立方根的近似值.
学习重难点
重点:正确理解立方根的概念,会用开立方运算求一个数的立方根.
难点:立方根和平方根的区别.
温故知新
1.你还记得什么是平方根吗?
2.平方根具有什么特征?
合作研究,获取新知
如图,要制作一个容积为27 cm3的正方体包装箱,它的棱长是多少?
解:设正方体的棱长为x cm,则
x3=27,
这就是要求一个数,使它的立方等于27.
因为 33=27,
所以 x=3
因此,正方体的棱长为3cm.
一、立方根的概念
通过上节课的学习,我们知道:
一般地,如果一个数的平方等于a,那么这个数叫作a的平方根,或二次方根.
即:若x2=a,则x是a的平方根(二次方根)
你能类比平方根的定义给出立方根的定义吗?
一般地,如果一个数的立方等于a,那么这个数叫作a的立方根,或三次方根.
即:若x3=a,则x是a的立方根(三次方根).
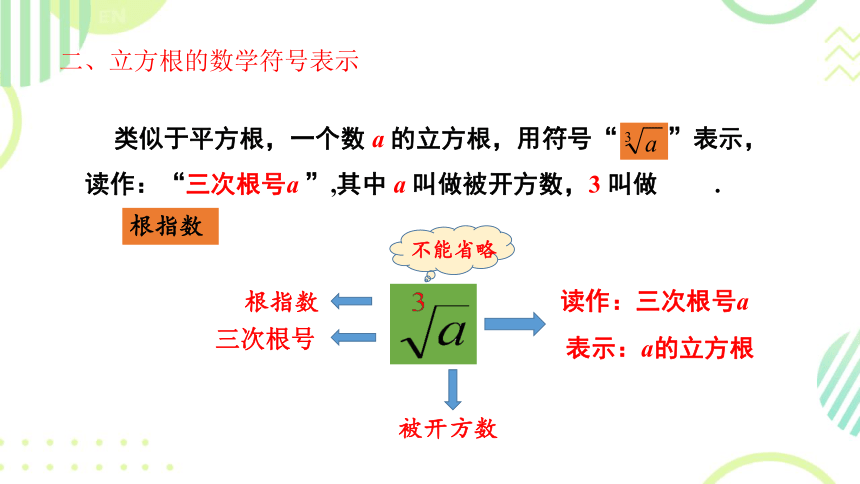
二、立方根的数学符号表示
类似于平方根,一个数 a 的立方根,用符号“ ”表示,读作:“三次根号a ”,其中 a 叫做被开方数,3 叫做 .
根指数
不能省略
根指数
三次根号
读作:三次根号a
表示:a的立方根
被开方数
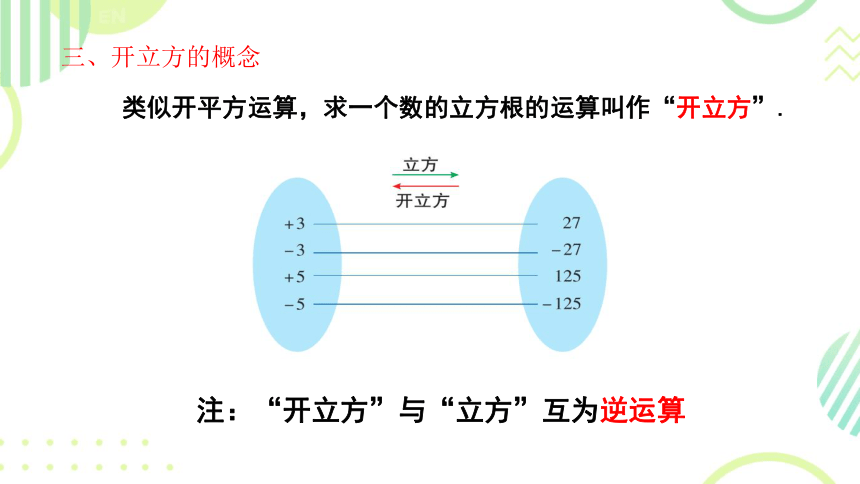
三、开立方的概念
类似开平方运算,求一个数的立方根的运算叫作“开立方”.
注:“开立方”与“立方”互为逆运算
探究新知
根据立方根的意义填空
你能归纳出立方根有什么特征吗?
1.因为 23 = 8,所以 8 的立方根是_______.
2.因为( )3 = 0.125,所以 0.125 的立方根是________.
3.因为 ( )3 = 0,所以 0 的立方根是_____.
4.因为( )3 = -8,所以 -8 的立方根是_______.
5.因为( )3 = ,所以 的立方根是_____.
2
0.5
0.5
0
-2
0
-2
探究新知
四、立方根的性质
正数的立方根是正数
负数的立方根是负数
0的立方根是0
你能说说数的平方根与数的立方根有什么不同吗?
探究新知
平方根与立方根的区别与联系
两个,互为相反数
一个,是正数
0
0
没有平方根
一个,是负数
非负数
可以为(任何数)
探究新知
-2
-2
=
-3
-3
=
互为相反数的两个数立方根也互为相反数。
例1. 的算数平方根是( )
五、典例精析
例2.求下列各式的值:
例3.计算:
2
探究新知
利用计算器求立方根
例4 用计算器求下列各数的立方根:343,-1.331.
解:依次按键:
解:依次按键:
显示:7
显示:-1.1
探究新知
小结:被开方数的小数点向左或向右移动3n位时立方根的
小数点就相应的向左或向右移动n位(n为正整数).
用你发现的规律填空: .
0.4642
0.04642
46.42
课堂互动
“知识配对”
VS
YOU
ME
1.求下列式中x的值.
(1)x3=0.008; (2)(x-1)3=27.
解析:(1)x =
∴ x = 0.2 ;
解析:(2)x-1 =
x = 3+1
∴x = 4
2. 已知x+3的平方根是±3,x-y 的立方根是 2,求x+y的算术平方根.
课堂小结
一般的,如果一个数的立方等于a,那么这个数叫做a的立方根或三次方根
正数的立方根是正数
负数的立方根是负数
0的立方根是0
第六章 实 数
6.2 立方根
学习目标
1.理解立方根的概念,会用根号表示一个数的立方根.会求一个数的立方根,了解开立方与立方互为逆运算.
2.掌握立方根的性质,能区分立方根与平方根的不同.通过类比平方根学习立方根,体会类比思想的运用.
3.会用计算器计算一个数的立方根或立方根的近似值.
学习重难点
重点:正确理解立方根的概念,会用开立方运算求一个数的立方根.
难点:立方根和平方根的区别.
温故知新
1.你还记得什么是平方根吗?
2.平方根具有什么特征?
合作研究,获取新知
如图,要制作一个容积为27 cm3的正方体包装箱,它的棱长是多少?
解:设正方体的棱长为x cm,则
x3=27,
这就是要求一个数,使它的立方等于27.
因为 33=27,
所以 x=3
因此,正方体的棱长为3cm.
一、立方根的概念
通过上节课的学习,我们知道:
一般地,如果一个数的平方等于a,那么这个数叫作a的平方根,或二次方根.
即:若x2=a,则x是a的平方根(二次方根)
你能类比平方根的定义给出立方根的定义吗?
一般地,如果一个数的立方等于a,那么这个数叫作a的立方根,或三次方根.
即:若x3=a,则x是a的立方根(三次方根).
二、立方根的数学符号表示
类似于平方根,一个数 a 的立方根,用符号“ ”表示,读作:“三次根号a ”,其中 a 叫做被开方数,3 叫做 .
根指数
不能省略
根指数
三次根号
读作:三次根号a
表示:a的立方根
被开方数
三、开立方的概念
类似开平方运算,求一个数的立方根的运算叫作“开立方”.
注:“开立方”与“立方”互为逆运算
探究新知
根据立方根的意义填空
你能归纳出立方根有什么特征吗?
1.因为 23 = 8,所以 8 的立方根是_______.
2.因为( )3 = 0.125,所以 0.125 的立方根是________.
3.因为 ( )3 = 0,所以 0 的立方根是_____.
4.因为( )3 = -8,所以 -8 的立方根是_______.
5.因为( )3 = ,所以 的立方根是_____.
2
0.5
0.5
0
-2
0
-2
探究新知
四、立方根的性质
正数的立方根是正数
负数的立方根是负数
0的立方根是0
你能说说数的平方根与数的立方根有什么不同吗?
探究新知
平方根与立方根的区别与联系
两个,互为相反数
一个,是正数
0
0
没有平方根
一个,是负数
非负数
可以为(任何数)
探究新知
-2
-2
=
-3
-3
=
互为相反数的两个数立方根也互为相反数。
例1. 的算数平方根是( )
五、典例精析
例2.求下列各式的值:
例3.计算:
2
探究新知
利用计算器求立方根
例4 用计算器求下列各数的立方根:343,-1.331.
解:依次按键:
解:依次按键:
显示:7
显示:-1.1
探究新知
小结:被开方数的小数点向左或向右移动3n位时立方根的
小数点就相应的向左或向右移动n位(n为正整数).
用你发现的规律填空: .
0.4642
0.04642
46.42
课堂互动
“知识配对”
VS
YOU
ME
1.求下列式中x的值.
(1)x3=0.008; (2)(x-1)3=27.
解析:(1)x =
∴ x = 0.2 ;
解析:(2)x-1 =
x = 3+1
∴x = 4
2. 已知x+3的平方根是±3,x-y 的立方根是 2,求x+y的算术平方根.
课堂小结
一般的,如果一个数的立方等于a,那么这个数叫做a的立方根或三次方根
正数的立方根是正数
负数的立方根是负数
0的立方根是0
