初中数学人教版七下6.3.1实数 课件(共25张PPT)
文档属性
| 名称 | 初中数学人教版七下6.3.1实数 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-22 18:38:00 | ||
图片预览






文档简介
(共25张PPT)
6.3 实 数
第1课时 实数
人教版·七年级下册
学习目标
02
进一步理解有理数和无理数的概念,会把实数进行分类;(重点)
03
理解实数与数轴的关系,并进行相关运用.(难点)
01
经历无理数的探究过程,理解无理数的概念,会判断一个数是否为无理数;(重点)
问题1 我们知道有理数包括整数和分数,请把下列分数写成小数的形式,你有什么发现?
思考导入
探究无理数的概念
问题2 整数能写成小数的形式吗?3可以看成是3.0吗?
可以
思考 由此你可以得到什么结论?
有理数都可以化成有限小数或无限循环小数的形式.
反过来,任何有限小数或无限循环小数也都是有理数.
讲授新课
一、无理数的概念
想一想:你认为小数除了上述类型外,还会有什么类型的小数
所有的数都可以写成有限小数和无限循环小数的形式吗?
无限不循环小数叫做无理数.
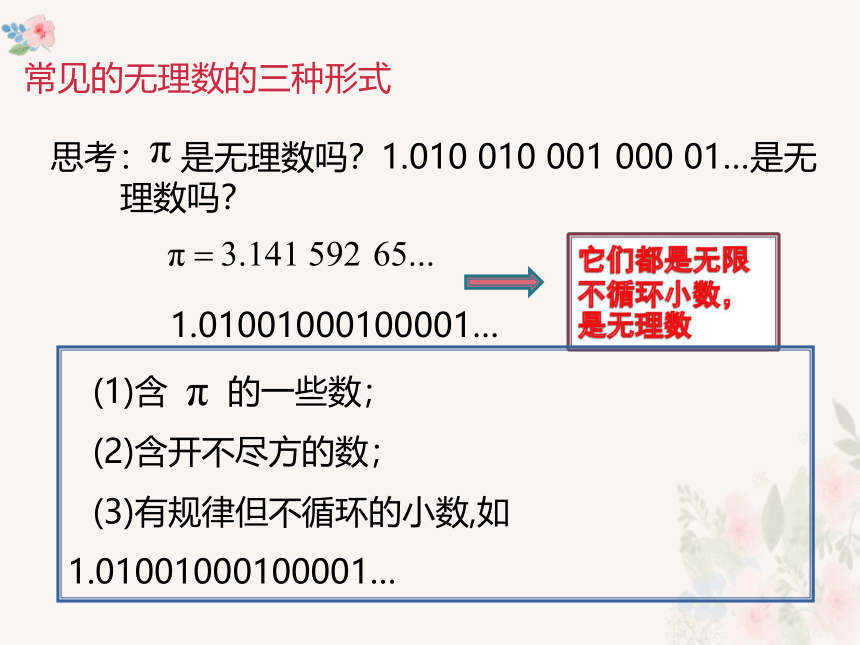
思考: 是无理数吗?1.010 010 001 000 01…是无
理数吗?
1.01001000100001…
(1)含 的一些数;
(2)含开不尽方的数;
(3)有规律但不循环的小数,如1.01001000100001…
常见的无理数的三种形式
我来做一做
1. 下列各数中,是无理数的是( )
A.3.1415 B. C. D.
2.下列各数:-2,0, , 0.010010001 , π, ,其中无理数的个数( )
A.4 B.3 C.2 D.1
D
C
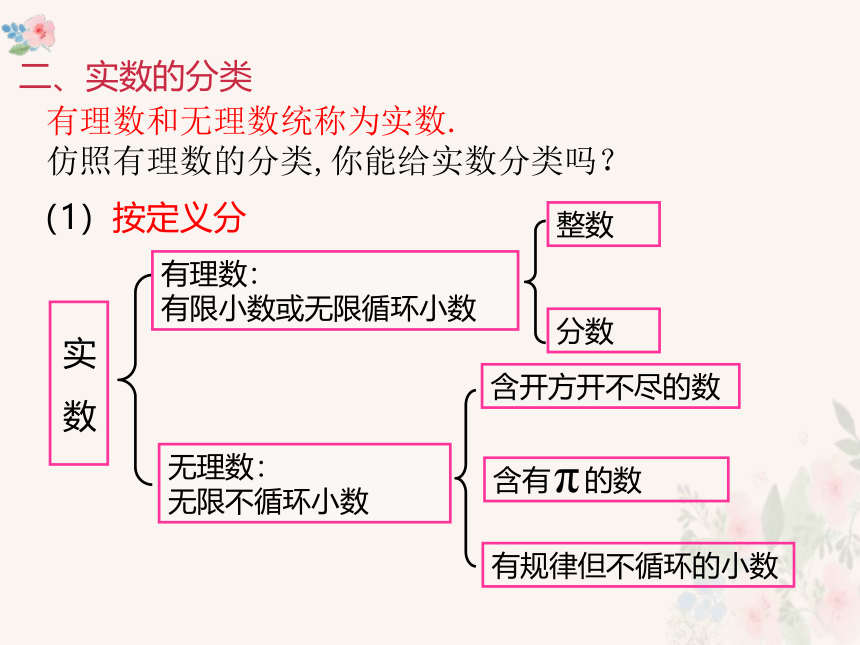
有理数和无理数统称为实数.
仿照有理数的分类,你能给实数分类吗?
无理数:
无限不循环小数
有理数:
有限小数或无限循环小数
实 数
(1)按定义分
分数
整数
含开方开不尽的数
有规律但不循环的小数
含有 的数
二、实数的分类
负实数
正实数
数实
正有理数
负有理数
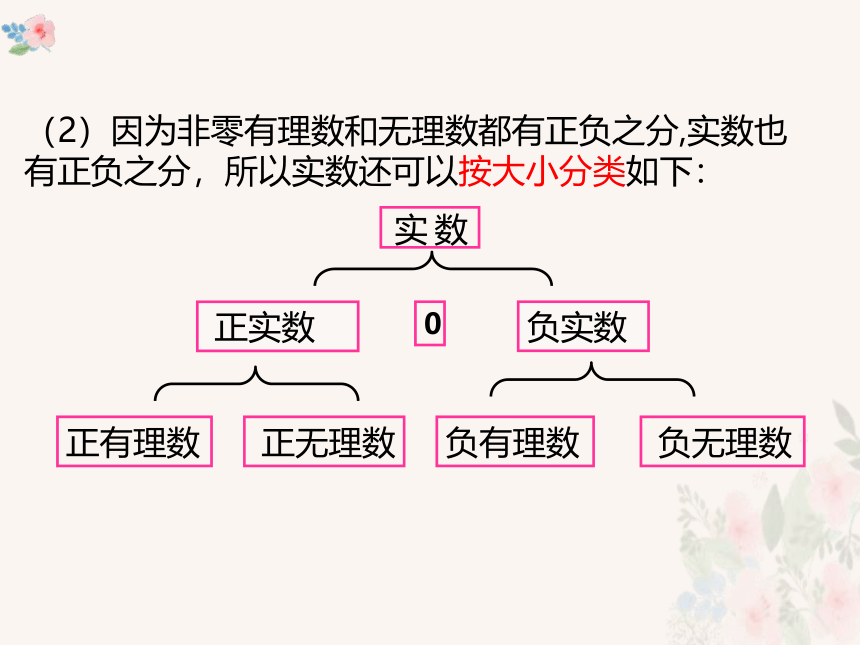
(2)因为非零有理数和无理数都有正负之分,实数也有正负之分,所以实数还可以按大小分类如下:
0
正无理数
负无理数
我来做一做
下列说法中,正确的是( )
A.无理数包括正无理数,零和负无理数
B.无限小数都是无理数
C.正实数包括正有理数和正无理数
D.实数可以分为正实数和负实数两类
C
无理数:
有理数:
负实数:
正实数:
例1 将下列各数分别填入下列相应的括号内:
典例精析
对每个数都要进行判断,分类标准不同结果不同.
我们知道,每个有理数都可以用数轴上的点来表示.
思考1:无理数是否也可以用数轴上的点表示出来呢?
探究:直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O' ,点O' 对应的数是多少?
这样,无理数π可以用数轴上的点来表示.
实数与数轴上的点的关系
三、
圆周长C=πd=π×1=π
从图中可以看出,OO'的长时这个圆的周长,所以点O' 对应的数是π
思考2:你能在数轴上表示出 和 - 吗?
以单位长度为边长画一个正方形,以原点为圆心,正方形的对角线为半径画弧,与正半轴的交点就表示 ,与负半轴的交点就表示- .(为什么)
用两个面积为1的小正方形可以拼成一个面积为2的大正方形,大正方形的边长是小正方形的对角线.
每一个无理数都可以用数轴上的一个点表示出来.
-2
-1
0
1
2
—
每一个实数都可以用数轴上的一个点来表示;
★实数与数轴上的点是一一对应的.
反过来,数轴上的每一点都表示一个实数.
与有理数一样,实数也可以比较大小:
实数的大小比较
与有理数规定的大小一样,数轴上右边的点表示的实数比左边的点表示的实数大.
原点
0
正实数
负实数
<
1.正数大于零,负数小于零,正数大于负数;
2.两个正数,绝对值大的数较大;
3.两个负数,绝对值大的数反而小.
与有理数一样,在实数范围内:
,2可以看作分别是面积为5,4的正方形的边长,容易说明:面积较大的正方形,它的边长也较大,因此
同样,因为5<9,所以
与2比较哪个大?与3比较呢?
议一议
典例精析
例2 在数轴上表示下列各点,比较它们的大小,
并用“<”连接它们.
-2 -1 0 1 2
1
-2
-2< < 1< <
例3 估计 位于( )
A.0~1之间 B.1~2之间 C.2~3之间 D.3~4之间
B
例4 比较下列各组数的大小:
解 : (1)因为 12 < 42,
所以 < 4,
所以 -1< 3;
(2)因为 10 > 32 ,
所以
所以
1.下列说法正确的是( )
A. a 一定是正实数
B. 是有理数
C. 有理数
D.数轴上任一点都对应一个有理数
B
当堂练习
2.有一个数值转换器,原理如下,当输x=81时,输出的y是 ( )
输入x
取算术平方根
是无理数
输出y
是有理数
A.9 B.3 C. D.±3
C
3.判断快枪手——看谁最快最准!
(1)实数不是有理数就是无理数. ( )
(2)无理数都是无限不循环小数. ( )
(4)无理数都是无限小数. ( )
(3)带根号的数都是无理数. ( )
(5)无理数一定都带根号. ( )
×
×
√
√
√
4.把下列各数填入相应的括号内:
(1)有理数: {
(2)无理数: {
(3)整数: {
(4)负数: {
(5)分数: {
(6)实数: {
}
}
}
}
}
}
5.比较 与 6 的大小
当堂练习
解: 因为 37 > 36
所以 > 6
课堂小结
通过本节课的学习,你觉得自己有哪些收获愿意和同学们一起分享呢?
1.两个概念:
无理数:无限不循环小数又叫做无理数
实 数:有理数和无理数统称为实数
2.实数的两种分类方法:
①根据实数的定义 ②根据实数的正负性
3.实数与数轴上的点成一一对应关系
完成配套作业
作业布置
6.3 实 数
第1课时 实数
人教版·七年级下册
学习目标
02
进一步理解有理数和无理数的概念,会把实数进行分类;(重点)
03
理解实数与数轴的关系,并进行相关运用.(难点)
01
经历无理数的探究过程,理解无理数的概念,会判断一个数是否为无理数;(重点)
问题1 我们知道有理数包括整数和分数,请把下列分数写成小数的形式,你有什么发现?
思考导入
探究无理数的概念
问题2 整数能写成小数的形式吗?3可以看成是3.0吗?
可以
思考 由此你可以得到什么结论?
有理数都可以化成有限小数或无限循环小数的形式.
反过来,任何有限小数或无限循环小数也都是有理数.
讲授新课
一、无理数的概念
想一想:你认为小数除了上述类型外,还会有什么类型的小数
所有的数都可以写成有限小数和无限循环小数的形式吗?
无限不循环小数叫做无理数.
思考: 是无理数吗?1.010 010 001 000 01…是无
理数吗?
1.01001000100001…
(1)含 的一些数;
(2)含开不尽方的数;
(3)有规律但不循环的小数,如1.01001000100001…
常见的无理数的三种形式
我来做一做
1. 下列各数中,是无理数的是( )
A.3.1415 B. C. D.
2.下列各数:-2,0, , 0.010010001 , π, ,其中无理数的个数( )
A.4 B.3 C.2 D.1
D
C
有理数和无理数统称为实数.
仿照有理数的分类,你能给实数分类吗?
无理数:
无限不循环小数
有理数:
有限小数或无限循环小数
实 数
(1)按定义分
分数
整数
含开方开不尽的数
有规律但不循环的小数
含有 的数
二、实数的分类
负实数
正实数
数实
正有理数
负有理数
(2)因为非零有理数和无理数都有正负之分,实数也有正负之分,所以实数还可以按大小分类如下:
0
正无理数
负无理数
我来做一做
下列说法中,正确的是( )
A.无理数包括正无理数,零和负无理数
B.无限小数都是无理数
C.正实数包括正有理数和正无理数
D.实数可以分为正实数和负实数两类
C
无理数:
有理数:
负实数:
正实数:
例1 将下列各数分别填入下列相应的括号内:
典例精析
对每个数都要进行判断,分类标准不同结果不同.
我们知道,每个有理数都可以用数轴上的点来表示.
思考1:无理数是否也可以用数轴上的点表示出来呢?
探究:直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O' ,点O' 对应的数是多少?
这样,无理数π可以用数轴上的点来表示.
实数与数轴上的点的关系
三、
圆周长C=πd=π×1=π
从图中可以看出,OO'的长时这个圆的周长,所以点O' 对应的数是π
思考2:你能在数轴上表示出 和 - 吗?
以单位长度为边长画一个正方形,以原点为圆心,正方形的对角线为半径画弧,与正半轴的交点就表示 ,与负半轴的交点就表示- .(为什么)
用两个面积为1的小正方形可以拼成一个面积为2的大正方形,大正方形的边长是小正方形的对角线.
每一个无理数都可以用数轴上的一个点表示出来.
-2
-1
0
1
2
—
每一个实数都可以用数轴上的一个点来表示;
★实数与数轴上的点是一一对应的.
反过来,数轴上的每一点都表示一个实数.
与有理数一样,实数也可以比较大小:
实数的大小比较
与有理数规定的大小一样,数轴上右边的点表示的实数比左边的点表示的实数大.
原点
0
正实数
负实数
<
1.正数大于零,负数小于零,正数大于负数;
2.两个正数,绝对值大的数较大;
3.两个负数,绝对值大的数反而小.
与有理数一样,在实数范围内:
,2可以看作分别是面积为5,4的正方形的边长,容易说明:面积较大的正方形,它的边长也较大,因此
同样,因为5<9,所以
与2比较哪个大?与3比较呢?
议一议
典例精析
例2 在数轴上表示下列各点,比较它们的大小,
并用“<”连接它们.
-2 -1 0 1 2
1
-2
-2< < 1< <
例3 估计 位于( )
A.0~1之间 B.1~2之间 C.2~3之间 D.3~4之间
B
例4 比较下列各组数的大小:
解 : (1)因为 12 < 42,
所以 < 4,
所以 -1< 3;
(2)因为 10 > 32 ,
所以
所以
1.下列说法正确的是( )
A. a 一定是正实数
B. 是有理数
C. 有理数
D.数轴上任一点都对应一个有理数
B
当堂练习
2.有一个数值转换器,原理如下,当输x=81时,输出的y是 ( )
输入x
取算术平方根
是无理数
输出y
是有理数
A.9 B.3 C. D.±3
C
3.判断快枪手——看谁最快最准!
(1)实数不是有理数就是无理数. ( )
(2)无理数都是无限不循环小数. ( )
(4)无理数都是无限小数. ( )
(3)带根号的数都是无理数. ( )
(5)无理数一定都带根号. ( )
×
×
√
√
√
4.把下列各数填入相应的括号内:
(1)有理数: {
(2)无理数: {
(3)整数: {
(4)负数: {
(5)分数: {
(6)实数: {
}
}
}
}
}
}
5.比较 与 6 的大小
当堂练习
解: 因为 37 > 36
所以 > 6
课堂小结
通过本节课的学习,你觉得自己有哪些收获愿意和同学们一起分享呢?
1.两个概念:
无理数:无限不循环小数又叫做无理数
实 数:有理数和无理数统称为实数
2.实数的两种分类方法:
①根据实数的定义 ②根据实数的正负性
3.实数与数轴上的点成一一对应关系
完成配套作业
作业布置
