初中数学人教版七下8.4三元一次方程组 课件(共20张PPT)
文档属性
| 名称 | 初中数学人教版七下8.4三元一次方程组 课件(共20张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-22 00:00:00 | ||
图片预览







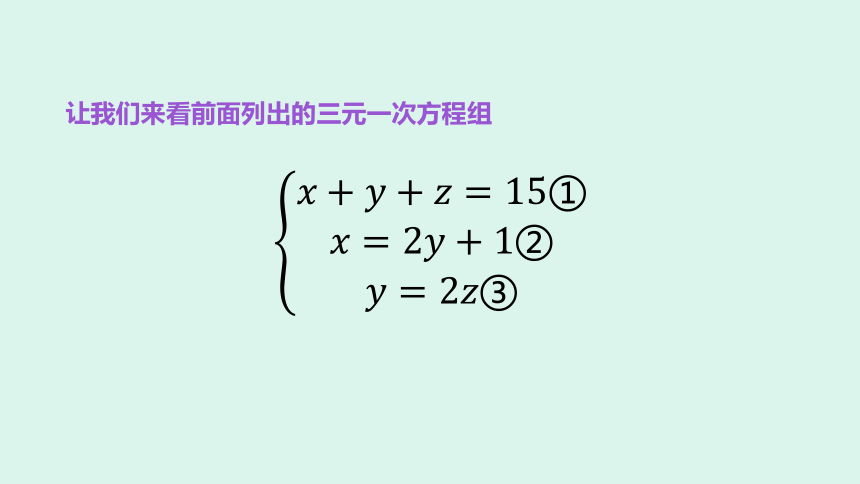

文档简介
第八章 二元一次方程组
*8.4 三元一次方程组的解法
01
02
能解简单的三元一次方程组
理解三元一次方程组的概念
学习目标
新课导入
在刚刚过去的2022北京冬奥会赛场上,我国运动员取得了历史最好成绩,斩获金牌、银牌、铜牌共15枚,其中,金牌数量是银牌数量2倍多1,银牌数量是铜牌数量的2倍,问:金、银、铜牌数量各几枚?
请同学们尝试求解
方法1:解:设铜牌x枚,则银牌2x枚,金牌(4x+1)枚.
根据题意可列方程:
x+2x+4x+1=15
解得x=2
2x=4, 4x+1=9
答:金牌9枚,银牌4枚,金牌2枚.
还有其他方法吗?能不能设多个未知数呢?
方法2:解:设金牌x枚,银牌y枚,铜牌z枚
根据题意可列方程: x+y+z=15
y=2z
x=2y+1
这个问题的解必须同时满足上面三个条件,因此,我们把这三个方程合在一起,写成
&????+????+????=15&????=2????+1&????=2????
?
这个方程组含有三个未知数,每个方程中含未知数的项的次数都 是1,并且一共有三个方程,像这样的方程组叫做三元一次方程组.
怎样解三元一次方程组呢?
(1)解二元一次方程组的基本方法有哪几种?
基本方法:代入法和加减法;
(2)它们的实质是什么?
实质:消元.
二元一次方程组
一元一次方程
消元
化归转化思想
回顾
代入消元法或者加减消元法对于解三元一次方程组适用吗?
让我们来看前面列出的三元一次方程组
&????+????+????=15①&????=2????+1②&????=2????③
?
仿照前面学过的代入法,我们可以先把 y=2z③代入②,得x=4z+1④,
再把y=2z③和x=4z+1④
代入①,得4z+1+2z+z=15
得z=2
再把z=2分别代入③,④得y=4,x=9
所以这个三元一次方程组的解为????=9????=4????=2
答:获得金牌9枚,银牌4枚,铜牌2枚.
?
请大家尝试解下面的三元一次方程组 ????+????+????=????????①????+????????+????????=????????????=?????????③②
它们组成方程组
?
对于这个方程组,消哪个元比较方便?理由是什么?
将③分别代入①②,得到两个只含y,z的方程:
&5????+????=12,&6????+5????=22.
?
得到二元一次方程组后,就不难求出y和z了,进而可求出x
&5????+????=12,④&6????+5????=22??⑤
?
具体过程如下:
????+????+????=????????①????+????????+????????=????????????=?????????③②
解:将③分别代入①②,得到两个只含y,z的方程:
?
&4????+????+????=12,&4????+2????+5????=22.
?
④×5,得?25????+5????=60⑥
⑥-⑤,得19y=38
得 y=2
把y=2代入④,得z=2
把y=2代入③,得x=8
因此这个三元一次方程组的解为 ????=8????=2????=2
?
即
① ② ③
如何用加减消元法解这个方程组?
③与④组成方程组
解这个方程组,得
解:① ②,得
④
把 x=8,y=2代入①,得
所以 z=2.
因此,这个三元一次方程组的解为
解三元一次方程组的基本思路是:通过“ ”或“ ”进行 ,把 转化为 ,使解三元一次方程组转化为解 ,进而再转化为解 .
三元一次方程组
二元一次方程组
一元一次方程
消元
消元
消元
三元
二元
二元一次方程组
一元一次方程
化归转化思想
归纳总结
代入
加减
例1 解三元一次方程组
解: ② ③,得
④
① ② ③
①与④组成方程组
解这个方程组,得
把 x=5,z=-2代入①,得
2×5+3?????2=9,
?
所以 y= .
因此,这个三元一次方程组的解为
你还有其他解法吗?试一试,并与这种解法进行比较?
所以这个方程组的解????=5????=13????=?2
?
方法2:
例2 在等式 y=ax2+bx+c中,当x=-1时,y=0;当x=2时,y=3;当x=5时,y=60. 求a,b,c的值.
解:根据题意,得三元一次方程组
a-b+c= 0, ①
4a+2b+c=3, ②
25a+5b+c=60. ③
②-①, 得 a+b=1 ④
③-①,得 4a+b=10 ⑤
④与⑤组成二元一次方程组
a+b=1,
4a+b=10.
解这个方程组,得????=3????=?2
?
把 ????=3????=?2 代入①,得c=-5
?
因此????=3????=?2????=?5
?
即a,b,c的值分别为3,-2,-5.
在古代数学著作《九章算术》中有一个问题译成汉语是这样的:
上等谷3束,中等谷2束,下等谷1束,可得粮食39斗;
上等谷2束,中等谷3束,下等谷1束,可得粮食34斗;
上等谷1束,中等谷2束,下等谷3束,可得粮食26斗.
求上、中、下三等谷每束各可得粮食几斗.
上等谷(束) 中等谷(束) 下等谷(束) 斗数
数学趣史
解:设每束上等谷、中等谷、下等谷各可得粮食x斗、y斗、z斗.
根据题意 ,得:
大家课下小组合作求解
三元一次方程组
三元一次方程组的概念
课堂小结
三元一次方程组的解法
作业见作业布置
*8.4 三元一次方程组的解法
01
02
能解简单的三元一次方程组
理解三元一次方程组的概念
学习目标
新课导入
在刚刚过去的2022北京冬奥会赛场上,我国运动员取得了历史最好成绩,斩获金牌、银牌、铜牌共15枚,其中,金牌数量是银牌数量2倍多1,银牌数量是铜牌数量的2倍,问:金、银、铜牌数量各几枚?
请同学们尝试求解
方法1:解:设铜牌x枚,则银牌2x枚,金牌(4x+1)枚.
根据题意可列方程:
x+2x+4x+1=15
解得x=2
2x=4, 4x+1=9
答:金牌9枚,银牌4枚,金牌2枚.
还有其他方法吗?能不能设多个未知数呢?
方法2:解:设金牌x枚,银牌y枚,铜牌z枚
根据题意可列方程: x+y+z=15
y=2z
x=2y+1
这个问题的解必须同时满足上面三个条件,因此,我们把这三个方程合在一起,写成
&????+????+????=15&????=2????+1&????=2????
?
这个方程组含有三个未知数,每个方程中含未知数的项的次数都 是1,并且一共有三个方程,像这样的方程组叫做三元一次方程组.
怎样解三元一次方程组呢?
(1)解二元一次方程组的基本方法有哪几种?
基本方法:代入法和加减法;
(2)它们的实质是什么?
实质:消元.
二元一次方程组
一元一次方程
消元
化归转化思想
回顾
代入消元法或者加减消元法对于解三元一次方程组适用吗?
让我们来看前面列出的三元一次方程组
&????+????+????=15①&????=2????+1②&????=2????③
?
仿照前面学过的代入法,我们可以先把 y=2z③代入②,得x=4z+1④,
再把y=2z③和x=4z+1④
代入①,得4z+1+2z+z=15
得z=2
再把z=2分别代入③,④得y=4,x=9
所以这个三元一次方程组的解为????=9????=4????=2
答:获得金牌9枚,银牌4枚,铜牌2枚.
?
请大家尝试解下面的三元一次方程组 ????+????+????=????????①????+????????+????????=????????????=?????????③②
它们组成方程组
?
对于这个方程组,消哪个元比较方便?理由是什么?
将③分别代入①②,得到两个只含y,z的方程:
&5????+????=12,&6????+5????=22.
?
得到二元一次方程组后,就不难求出y和z了,进而可求出x
&5????+????=12,④&6????+5????=22??⑤
?
具体过程如下:
????+????+????=????????①????+????????+????????=????????????=?????????③②
解:将③分别代入①②,得到两个只含y,z的方程:
?
&4????+????+????=12,&4????+2????+5????=22.
?
④×5,得?25????+5????=60⑥
⑥-⑤,得19y=38
得 y=2
把y=2代入④,得z=2
把y=2代入③,得x=8
因此这个三元一次方程组的解为 ????=8????=2????=2
?
即
① ② ③
如何用加减消元法解这个方程组?
③与④组成方程组
解这个方程组,得
解:① ②,得
④
把 x=8,y=2代入①,得
所以 z=2.
因此,这个三元一次方程组的解为
解三元一次方程组的基本思路是:通过“ ”或“ ”进行 ,把 转化为 ,使解三元一次方程组转化为解 ,进而再转化为解 .
三元一次方程组
二元一次方程组
一元一次方程
消元
消元
消元
三元
二元
二元一次方程组
一元一次方程
化归转化思想
归纳总结
代入
加减
例1 解三元一次方程组
解: ② ③,得
④
① ② ③
①与④组成方程组
解这个方程组,得
把 x=5,z=-2代入①,得
2×5+3?????2=9,
?
所以 y= .
因此,这个三元一次方程组的解为
你还有其他解法吗?试一试,并与这种解法进行比较?
所以这个方程组的解????=5????=13????=?2
?
方法2:
例2 在等式 y=ax2+bx+c中,当x=-1时,y=0;当x=2时,y=3;当x=5时,y=60. 求a,b,c的值.
解:根据题意,得三元一次方程组
a-b+c= 0, ①
4a+2b+c=3, ②
25a+5b+c=60. ③
②-①, 得 a+b=1 ④
③-①,得 4a+b=10 ⑤
④与⑤组成二元一次方程组
a+b=1,
4a+b=10.
解这个方程组,得????=3????=?2
?
把 ????=3????=?2 代入①,得c=-5
?
因此????=3????=?2????=?5
?
即a,b,c的值分别为3,-2,-5.
在古代数学著作《九章算术》中有一个问题译成汉语是这样的:
上等谷3束,中等谷2束,下等谷1束,可得粮食39斗;
上等谷2束,中等谷3束,下等谷1束,可得粮食34斗;
上等谷1束,中等谷2束,下等谷3束,可得粮食26斗.
求上、中、下三等谷每束各可得粮食几斗.
上等谷(束) 中等谷(束) 下等谷(束) 斗数
数学趣史
解:设每束上等谷、中等谷、下等谷各可得粮食x斗、y斗、z斗.
根据题意 ,得:
大家课下小组合作求解
三元一次方程组
三元一次方程组的概念
课堂小结
三元一次方程组的解法
作业见作业布置
