初中数学人教版七下5.1.2垂线(1) 教案
文档属性
| 名称 | 初中数学人教版七下5.1.2垂线(1) 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 414.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-22 20:42:33 | ||
图片预览


文档简介
5.1.2垂线
一、教学内容分析
本节内容是在学生已有的相交线知识的学习和小学学过的垂线的经验的基础上学习的,学生有一定的画图、识图基础,垂直的概念承接了前面学段学过的两条直线垂直的定义,基础层面的知识不难理解,但垂线的画法、性质和垂直的符号语言和图形语言的表示,仍然需要认真理解并掌握,并引导学生有条理的思考和表达,有意识的培养学生的推理能力.
二、教学目标
1.理解垂线的有关概念,会用三角板或量角器过一点画已知直线的垂线.在观察、测量、画图等数学活动中,感受数学知识与生活的联系,经历认识垂线的过程,培养观察能力、探究能力和判断能力.
2.掌握垂线的性质:在同一平面内,过一点有且只有一条直线与已知直线垂直.通过画图总结归纳性质,培养学习“空间与图形”的兴趣.
三、教学重难点
【重点】垂线的有关概念、画法及性质.
【难点】垂线的画法.
四、教学方法
启发法、演示法、课堂讨论法.
五、教学过程
(一)新课导入
多媒体出示一张照片,问:
你知道这是什么吗?
如图中的两条直线的关系很常见,观察你所处环境,能再举出其他例子吗?
意图:通过冬奥会的会馆冰立方引入垂直,激发学生爱国情怀和学习积极性.让学生在自己所处环境中寻找例子,训练学生观察能力.
效果:让学生体会到垂直作为两条直线相交的特殊情形,在生活中有着广泛的应用.
(二)新课讲授
1.垂线的有关概念
动手:回忆上节课学习的相交线的知识,引导学生在练习本上画出不同情况的相交线,分类汇总不同的画法,通过测量夹角的度数,观察两条直线的位置关系.
观察:在学生画图的基础上,教师演示在相交线的模型中,固定木条a,转动木条b,当b的位置变化时,a、b所成的∠α也会发生变化.
总结:当∠α=90°时,就说a与b互相垂直,记作a⊥b.
垂直是相交的一种特殊情形.
意图:通过自己画图和木条转动,让学生充分体会随着转动角度的变化,由两条直线相交到两条直线垂直的变化过程,理解垂直是相交的一种特殊情形,进而体会一般到特殊的研究问题的方法.
效果:通过观察、思考,理解动中有静,一般到特殊的学习研究问题的方法.
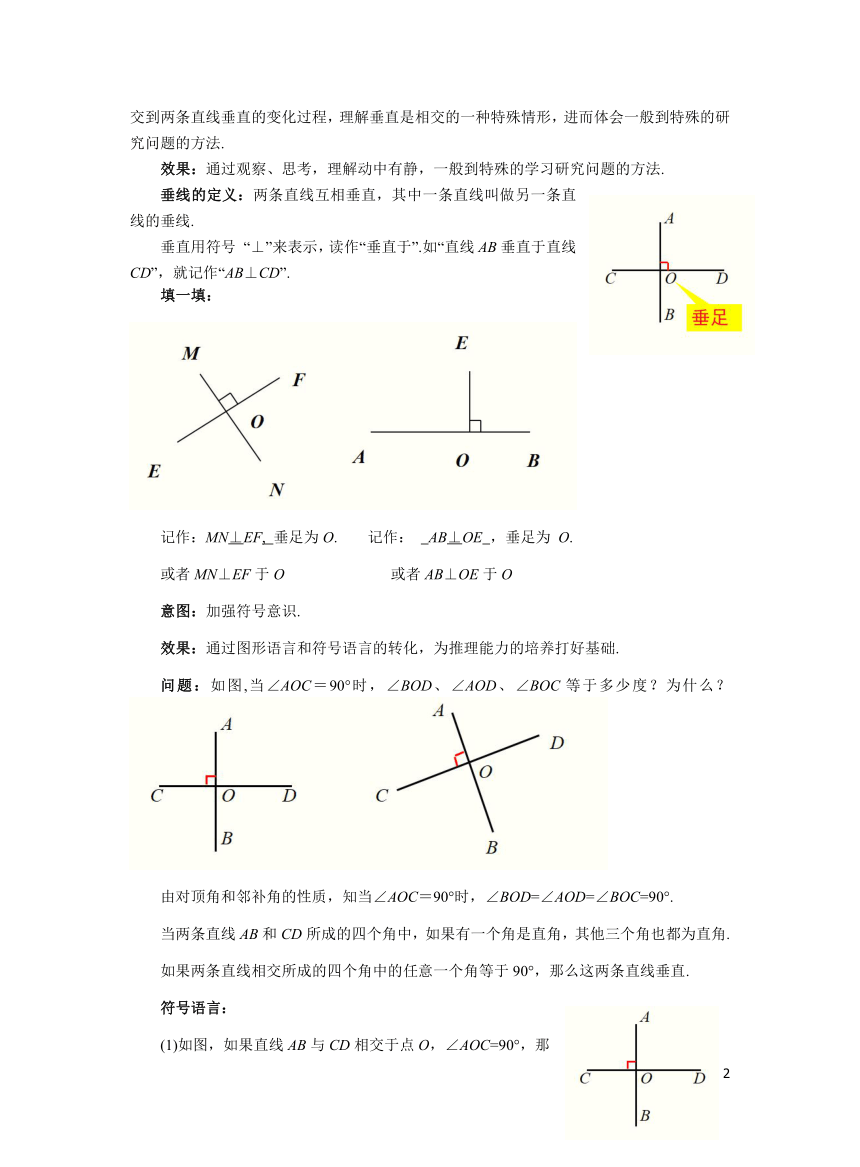
垂线的定义:两条直线互相垂直,其中一条直线叫做另一条直线的垂线.
垂直用符号 “⊥”来表示,读作“垂直于”.如“直线AB垂直于直线CD”,就记作“AB⊥CD”.
填一填:
记作:MN⊥EF, 垂足为O. 记作: AB⊥OE ,垂足为 O.
或者MN⊥EF于O 或者AB⊥OE于O
意图:加强符号意识.
效果:通过图形语言和符号语言的转化,为推理能力的培养打好基础.
问题:如图,当∠AOC=90°时,∠BOD、∠AOD、∠BOC等于多少度?为什么?
由对顶角和邻补角的性质,知当∠AOC=90°时,∠BOD=∠AOD=∠BOC=90°.
当两条直线AB和CD所成的四个角中,如果有一个角是直角,其他三个角也都为直角.
如果两条直线相交所成的四个角中的任意一个角等于90°,那么这两条直线垂直.
符号语言:
(1)如图,如果直线AB与CD相交于点O,∠AOC=90°,那么AB⊥CD.
∵∠AOC=90°,(已知)
∴AB⊥CD.(垂直的定义)
(2)如图,如果直线AB与CD相交于点O,AB⊥CD,那么∠AOC=90°.
∵ AB⊥CD ,(已知)
∴ ∠AOC=90° .(垂直的定义)
(∠AOD=∠BOC=∠BOD=90°)
意图:理解定义包含的两层意义,加强符号意识的训练.
效果:既理解垂直的两层含义,又能初步理解什么是推理,最终做到用符号表示推理,培养推理能力.
做一做:
如图,若直线m、n相交于点O,∠1=90°,则 m⊥n ;
若直线AB、CD相交于点O,且AB⊥CD,那么∠BOD =90°;
(3)如图,已知AB⊥CD,垂足为O,OE是一条射线,且∠AOE=35°,求∠BOE、∠COE的度数.
解:∵ AB⊥CD ∴∠AOC=90°
∵∠AOE=35°
∴∠COE=55°
∴∠BOE=∠BOC+∠COE=145°
意图:练习垂直定义的两个意义.
效果:对垂直定义的学以致用.
2.垂线的画法
问题:
(1)用三角板或量角器画已知直线l的垂线能画几条
(2)经过直线l上的一点A画l的垂线,这样的垂线能画几条
(3)经过直线l外的一点B画l的垂线,这样的垂线能画几条
(1)如图,已知直线l,作l的垂线.
①靠 ②画
问题:这样画l的垂线可以画几条?(无数条)
(2)如图,已知直线 l 和l上的一点A ,作l的垂线.
①靠(线)②移(三角板)③过(点)④画(线)
问题:这样画l的垂线可以画几条?(一条)
(3)如图,已知直线 l 和l外的一点A ,作l的垂线.
①靠(线)②移(三角板)③过(点)④画(线)
问题:这样画l的垂线可以画几条?一条
讨论:你会用量角器画图吗?画图的依据是什么?
根据以上操作,你能得出什么结论?
3.垂线的性质
基本事实:在同一平面内,过一点有且只有一条直线与已知直线垂直.
注意:
(1)强调“在同一平面内”;
(2)“过一点”中的点,可以在已知直线上,也可以在已知直线外;
(3)“有且只有”中,“有”指存在,“只有”指唯一性.
意图:具体分析几何语言,提高学生读题的能力.
效果:引导学生理解几何语言的准确性和严谨性.
选一选
过点P 向线段AB 所在直线引垂线,正确的是( C)
画一画
画一条线段或射线的垂线,就是画它们所在直线的垂线.如图,请你过点P画出射线AB
或线段AB的垂线.
意图:提高学生识图和画图能力.
效果:提高画图能力,深刻理解垂线的画法和垂直的定义.
(三)课堂练习
1.两条直线相交所成的四个角中,下列条件中能判定两条直线垂直的是( C )
A. 有两个角相等 B.有两对角相等
C. 有三个角相等 D.有四对邻补角
2.如图 ,已知AB与CD相交于O, OE⊥CD于O,∠AOC=36°,则∠BOE= ( D )
A.36° B. 64° C.144° D.54°
3.如图,已知直线AB、CD都经过O 点,OE为射线,若∠1=35°,∠2=55°,则OE与AB的位置关是垂直 .
.
4.已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是( B)
A.相等 B.互余 C.互补 D.互为对顶角
意图:检测和巩固本节所学知识.
(四)课堂小结
先让学生自己总结反思,然后同学之间进行交流,再找学生谈谈自己的收获.
1.垂线的有关概念
2.垂线的画法
①放;②靠;③移 ;④画.
3.垂线的性质
在同一平面内,过一点有且只有一条直线与已知直线垂直.
意图:总结反思是一节课必不可少的环节,有助于学生巩固所学,并检验自己不懂的地方是否弄明白.
(五)作业布置
完成配套作业
六、板书设计
5.1.2垂线
1.垂线的有关概念:垂直、垂线、垂足
符号语言:
2.垂线的画法:
①放;②靠;③移 ;④画.
3.垂线的性质
基本事实:在同一平面内,过一点有且只有一条直线与已知直线垂直.
课后反思
我们知道教学的任务是解决学生现有的认知水平和教育要求之间的矛盾,要为了学习而设计教学,是教学设计的出发点. 对于七年级的学生来说,抽象能力和几何语言表达能力较弱,教学活动中要让学生多看一看、说一说、画一画、想一想.
A
B
E
D
C
O
1
一、教学内容分析
本节内容是在学生已有的相交线知识的学习和小学学过的垂线的经验的基础上学习的,学生有一定的画图、识图基础,垂直的概念承接了前面学段学过的两条直线垂直的定义,基础层面的知识不难理解,但垂线的画法、性质和垂直的符号语言和图形语言的表示,仍然需要认真理解并掌握,并引导学生有条理的思考和表达,有意识的培养学生的推理能力.
二、教学目标
1.理解垂线的有关概念,会用三角板或量角器过一点画已知直线的垂线.在观察、测量、画图等数学活动中,感受数学知识与生活的联系,经历认识垂线的过程,培养观察能力、探究能力和判断能力.
2.掌握垂线的性质:在同一平面内,过一点有且只有一条直线与已知直线垂直.通过画图总结归纳性质,培养学习“空间与图形”的兴趣.
三、教学重难点
【重点】垂线的有关概念、画法及性质.
【难点】垂线的画法.
四、教学方法
启发法、演示法、课堂讨论法.
五、教学过程
(一)新课导入
多媒体出示一张照片,问:
你知道这是什么吗?
如图中的两条直线的关系很常见,观察你所处环境,能再举出其他例子吗?
意图:通过冬奥会的会馆冰立方引入垂直,激发学生爱国情怀和学习积极性.让学生在自己所处环境中寻找例子,训练学生观察能力.
效果:让学生体会到垂直作为两条直线相交的特殊情形,在生活中有着广泛的应用.
(二)新课讲授
1.垂线的有关概念
动手:回忆上节课学习的相交线的知识,引导学生在练习本上画出不同情况的相交线,分类汇总不同的画法,通过测量夹角的度数,观察两条直线的位置关系.
观察:在学生画图的基础上,教师演示在相交线的模型中,固定木条a,转动木条b,当b的位置变化时,a、b所成的∠α也会发生变化.
总结:当∠α=90°时,就说a与b互相垂直,记作a⊥b.
垂直是相交的一种特殊情形.
意图:通过自己画图和木条转动,让学生充分体会随着转动角度的变化,由两条直线相交到两条直线垂直的变化过程,理解垂直是相交的一种特殊情形,进而体会一般到特殊的研究问题的方法.
效果:通过观察、思考,理解动中有静,一般到特殊的学习研究问题的方法.
垂线的定义:两条直线互相垂直,其中一条直线叫做另一条直线的垂线.
垂直用符号 “⊥”来表示,读作“垂直于”.如“直线AB垂直于直线CD”,就记作“AB⊥CD”.
填一填:
记作:MN⊥EF, 垂足为O. 记作: AB⊥OE ,垂足为 O.
或者MN⊥EF于O 或者AB⊥OE于O
意图:加强符号意识.
效果:通过图形语言和符号语言的转化,为推理能力的培养打好基础.
问题:如图,当∠AOC=90°时,∠BOD、∠AOD、∠BOC等于多少度?为什么?
由对顶角和邻补角的性质,知当∠AOC=90°时,∠BOD=∠AOD=∠BOC=90°.
当两条直线AB和CD所成的四个角中,如果有一个角是直角,其他三个角也都为直角.
如果两条直线相交所成的四个角中的任意一个角等于90°,那么这两条直线垂直.
符号语言:
(1)如图,如果直线AB与CD相交于点O,∠AOC=90°,那么AB⊥CD.
∵∠AOC=90°,(已知)
∴AB⊥CD.(垂直的定义)
(2)如图,如果直线AB与CD相交于点O,AB⊥CD,那么∠AOC=90°.
∵ AB⊥CD ,(已知)
∴ ∠AOC=90° .(垂直的定义)
(∠AOD=∠BOC=∠BOD=90°)
意图:理解定义包含的两层意义,加强符号意识的训练.
效果:既理解垂直的两层含义,又能初步理解什么是推理,最终做到用符号表示推理,培养推理能力.
做一做:
如图,若直线m、n相交于点O,∠1=90°,则 m⊥n ;
若直线AB、CD相交于点O,且AB⊥CD,那么∠BOD =90°;
(3)如图,已知AB⊥CD,垂足为O,OE是一条射线,且∠AOE=35°,求∠BOE、∠COE的度数.
解:∵ AB⊥CD ∴∠AOC=90°
∵∠AOE=35°
∴∠COE=55°
∴∠BOE=∠BOC+∠COE=145°
意图:练习垂直定义的两个意义.
效果:对垂直定义的学以致用.
2.垂线的画法
问题:
(1)用三角板或量角器画已知直线l的垂线能画几条
(2)经过直线l上的一点A画l的垂线,这样的垂线能画几条
(3)经过直线l外的一点B画l的垂线,这样的垂线能画几条
(1)如图,已知直线l,作l的垂线.
①靠 ②画
问题:这样画l的垂线可以画几条?(无数条)
(2)如图,已知直线 l 和l上的一点A ,作l的垂线.
①靠(线)②移(三角板)③过(点)④画(线)
问题:这样画l的垂线可以画几条?(一条)
(3)如图,已知直线 l 和l外的一点A ,作l的垂线.
①靠(线)②移(三角板)③过(点)④画(线)
问题:这样画l的垂线可以画几条?一条
讨论:你会用量角器画图吗?画图的依据是什么?
根据以上操作,你能得出什么结论?
3.垂线的性质
基本事实:在同一平面内,过一点有且只有一条直线与已知直线垂直.
注意:
(1)强调“在同一平面内”;
(2)“过一点”中的点,可以在已知直线上,也可以在已知直线外;
(3)“有且只有”中,“有”指存在,“只有”指唯一性.
意图:具体分析几何语言,提高学生读题的能力.
效果:引导学生理解几何语言的准确性和严谨性.
选一选
过点P 向线段AB 所在直线引垂线,正确的是( C)
画一画
画一条线段或射线的垂线,就是画它们所在直线的垂线.如图,请你过点P画出射线AB
或线段AB的垂线.
意图:提高学生识图和画图能力.
效果:提高画图能力,深刻理解垂线的画法和垂直的定义.
(三)课堂练习
1.两条直线相交所成的四个角中,下列条件中能判定两条直线垂直的是( C )
A. 有两个角相等 B.有两对角相等
C. 有三个角相等 D.有四对邻补角
2.如图 ,已知AB与CD相交于O, OE⊥CD于O,∠AOC=36°,则∠BOE= ( D )
A.36° B. 64° C.144° D.54°
3.如图,已知直线AB、CD都经过O 点,OE为射线,若∠1=35°,∠2=55°,则OE与AB的位置关是垂直 .
.
4.已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是( B)
A.相等 B.互余 C.互补 D.互为对顶角
意图:检测和巩固本节所学知识.
(四)课堂小结
先让学生自己总结反思,然后同学之间进行交流,再找学生谈谈自己的收获.
1.垂线的有关概念
2.垂线的画法
①放;②靠;③移 ;④画.
3.垂线的性质
在同一平面内,过一点有且只有一条直线与已知直线垂直.
意图:总结反思是一节课必不可少的环节,有助于学生巩固所学,并检验自己不懂的地方是否弄明白.
(五)作业布置
完成配套作业
六、板书设计
5.1.2垂线
1.垂线的有关概念:垂直、垂线、垂足
符号语言:
2.垂线的画法:
①放;②靠;③移 ;④画.
3.垂线的性质
基本事实:在同一平面内,过一点有且只有一条直线与已知直线垂直.
课后反思
我们知道教学的任务是解决学生现有的认知水平和教育要求之间的矛盾,要为了学习而设计教学,是教学设计的出发点. 对于七年级的学生来说,抽象能力和几何语言表达能力较弱,教学活动中要让学生多看一看、说一说、画一画、想一想.
A
B
E
D
C
O
1
