初中数学人教版七下8.3.1实际问题与二元一次方程组 教案
文档属性
| 名称 | 初中数学人教版七下8.3.1实际问题与二元一次方程组 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 177.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-22 00:00:00 | ||
图片预览


文档简介
8.3.1实际问题与二元一次方程组
一、教材分析
《实际问题与二元一次方程组》是人民教育出版社七年级(下)第八章《二元一次方程组》第三节.本节内容安排了2个课时完成,是在学生掌握了二元一次方程组的解法,能列二元一次方程组解较简单的实际问题的基础上安排的,其中的“和差倍分问题”“几何问题”“行程问题”是具有一定综合性的问题.本课时选择了两个且有一定综合性的问题,“牛饲料问题”“种植计划问题”.让学生以方程组为工具进行一定深度的思考,丰富运用方程组解决实际问题的实践,把本章强调的以方程组为工具,实际问题模型化的思想提到新的高度.为切实提高利用方程组解决实际问题的能力,这节内容的问题形式包括,估算与精确计算的比较(探究1),开放地寻求设计方案(探究2),本节目的在于,一方面通过实际生活中的问题,进一步突出方程组这种数学模型应用的广泛性和有效性;另一方面使学生在实际问题情境中运用所学数学知识,进一步提高分析问题和解决问题的能力.
二、教学目标
1.学会利用二元一次方程组解决和、差、倍、分问题,几何问题和行程问题.
2.经历探索用二元一次方程组解决实际问题的过程,进一步提高分析问题中数量关系、设未知数、列方程组、解方程组的能力,体会数学建模思想.
三、教学重难点
【重点】会利用二元一次方程组解决和、差、倍、分问题,几何问题和行程问题.
【难点】正确找出问题中的两个等量关系,体会数学建模思想.
四、教学方法
探究式学习法、讲练结合法.
五、教学过程
(一)新课导入
视频导入
多媒体播放《奔跑吧,兄弟》的某段视频,引出“鸡兔同笼问题”,问:视频中的问题你知道怎么解吗?
意图:以视频方式引出二元一次方程组可以顺利解决“鸡兔同笼问题”.让学生充分表达自己的想法,部分学生可能用算数的方法,也可能用方程组,学生初步感知算数和方程组解决实际问题的异同,发现方程组和方程是数学的进步.
效果:通过视频导入这个环节,激发了学生本节课的学习兴趣,活跃了课堂氛围.以熟悉的问题为背景,让学生感受到这节课并不陌生,让学生有种亲切感,更易于接受新的概念,对本节课的学习增强了信心.
(二)探究新知
1.列方程组解决和、差、倍、分问题
出示教材的探究1
养牛场原有30只大牛和15只小牛,1天约用饲料675 kg;一周后又购进12只大牛和5只小牛,这时1天约用饲料940 kg.饲养员李大叔估计每只大牛1天约需饲料18到20 kg,每只小牛1天约需饲料7到8 kg.你认为李大叔估计的准确吗?
教师出示两个问题:
问题1 如何理解“通过计算检验他的估计”这句话?
问题2 题目中有哪些未知量?你如何设未知数?题目中有哪些等量关系?
(学生自由发言)
意图:教师提出两个问题,问题1让学生体会对于估算的结果要通过精确求职来检验,理解要想检验估计是否准确,需要求出大牛、小牛1天所需要的饲料;问题2重在引导学生发现问题中的已知量和未知量,寻找等量关系,借助二元一次方程组进行计算.
效果:学生独立探究,合作交流.让学生学会分析问题中的数量关系,发现等量关系,体会数学建模的关键过程.
问题3 如何解决这个问题?
学生依据发现的等量关系,建立方程组.
设每头大牛和小牛平均1天各需用饲料为x kg和y kg,根据等量关系,列方程组:
追问:你是如何解这个方程组的?列一元一次方程能解决这个问题吗?
意图:学生独立解方程组,并发言交流.让学生经历分析数量关系,得到数量关系,列方程组的过程.一般情况下,学生会自觉选择列方程组解决.
效果:学生通过交流对比发现,由实际问题列出的方程组,有时系数较为复杂,先化简再求解,可以简化运算.学生体会到有两个未知量时列方程组更为简单.
出示剧情发展:随着养牛场规模逐渐扩大,李大叔需聘请饲养员协助管理现有的42头大牛和20头小牛,已知甲种饲养员每人可负责8头大牛和4头小牛,乙种饲养员每人可负责5头大牛和2头小牛,请问李大叔应聘请甲乙两种饲养员各多少人?
总结归纳:
用二元一次方程组解决实际问题的步骤:
(1)审题:弄清题意和题目中的 数量关系;
(2)设元:用 字母 表示题目中的未知数;
(3)列方程组:根据 2 个等量关系列出方程组;
(4)解方程组:利用 代入消元 法或 加减消元 法解出未知数的值;
(5)检验并答:检验所求的解是否符合实际意义,然后作答.
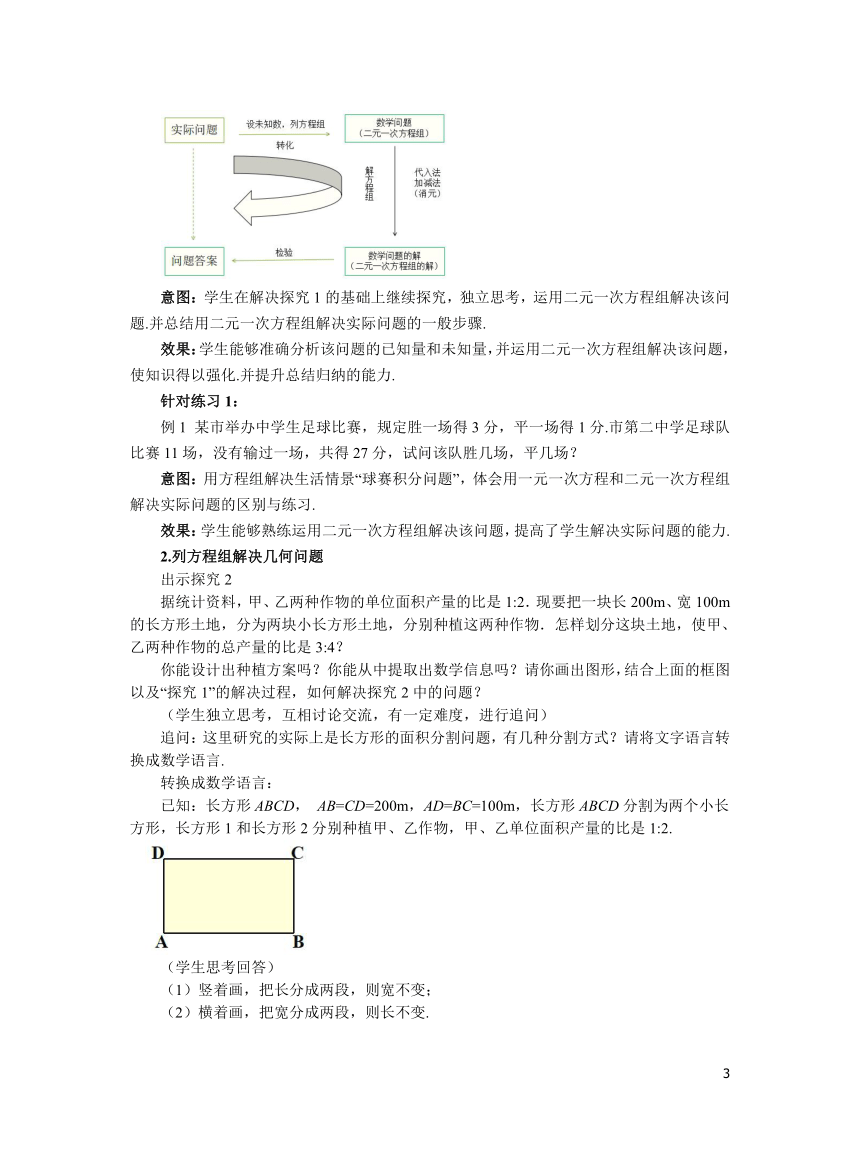
意图:学生在解决探究1的基础上继续探究,独立思考,运用二元一次方程组解决该问题.并总结用二元一次方程组解决实际问题的一般步骤.
效果:学生能够准确分析该问题的已知量和未知量,并运用二元一次方程组解决该问题,使知识得以强化.并提升总结归纳的能力.
针对练习1:
例1 某市举办中学生足球比赛,规定胜一场得3分,平一场得1分.市第二中学足球队比赛11场,没有输过一场,共得27分,试问该队胜几场,平几场?
意图:用方程组解决生活情景“球赛积分问题”,体会用一元一次方程和二元一次方程组解决实际问题的区别与练习.
效果:学生能够熟练运用二元一次方程组解决该问题,提高了学生解决实际问题的能力.
2.列方程组解决几何问题
出示探究2
据统计资料,甲、乙两种作物的单位面积产量的比是1:2.现要把一块长200m、宽100m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
你能设计出种植方案吗?你能从中提取出数学信息吗?请你画出图形,结合上面的框图以及“探究1”的解决过程,如何解决探究2中的问题?
(学生独立思考,互相讨论交流,有一定难度,进行追问)
追问:这里研究的实际上是长方形的面积分割问题,有几种分割方式?请将文字语言转换成数学语言.
转换成数学语言:
已知:长方形ABCD, AB=CD=200m,AD=BC=100m,长方形ABCD分割为两个小长方形,长方形1和长方形2分别种植甲、乙作物,甲、乙单位面积产量的比是1:2.
(学生思考回答)
(1)竖着画,把长分成两段,则宽不变;
(2)横着画,把宽分成两段,则长不变.
学生画图分析题意,上板写出解题过程,并进行解析.
意图:让学生经历列方程组解决实际问题的完整过程,一题多解,体现思维的多样性.效果:学生互相交流,互相启发,不断完善种植方案,经历列方程组解决实际问题的过程,加深对建模一般步骤的理解.
针对练习2
8块相同的小长方形地砖拼成一个大长方形,每块小长方形地砖的长和宽分别是多少?(单位cm)
解析:
直接设:小长方形地砖的长为x, 宽为y.
等量关系为:
(小长方形的一个长)+(小长方形的一个宽)= 大长方形的宽60;
小长方形的长 = 小长方形3个宽.
学生观察图形,发现几何拼图中隐藏的等量关系,列出方程组求解.
意图:对探究2作针对练习,用方程组解决几何中的拼图问题.
效果:培养学生的观察能力,应用方程组解决几何问题的能力.
3.列方程组解决行程问题
探究3
小华从家里到学校的路是一段平路和一段下坡路. 假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问小华家离学校多远?
通过画线段图的方法表示从家到学校的路途,分析往返途中的两个等量关系,列方程组.
等量关系:从家里到学校:走平路的时间+走下坡路的时间= 10 ;
从学校到家里:走上坡路的时间+走平路的时间= 15 .
方法一(直接设元法)
解:设小华家到学校平路长x m,下坡路长y m.
根据题意,可列方程组:
解方程组,得
所以,x+y=300+400=700.
答:小明家到学校的距离为700m.
方法二(间接设元法)
解:设小华下坡路所花时间为x min,上坡路所花时间为y min.
根据题意,可列方程组:
解方程组,得
所以坡路距离:80×5=400(m),平路距离:60×(10-5)=300(m)
所以,小明家到学校的距离为700m.
意图:遇到行程问题,经常会设不同的未知数,让学生大胆尝试,感受直接设元和间接设元的不同.
效果:用画线段图和列表的方法,来减小坡度、分散难点,另一方面利用画图来引导学生学会分析和表达.
针对练习3
例2 甲、乙两人相距4km,以各自的速度同时出发.如果同向而行,甲2h追上乙;如果相向而行,两人0.5h后相遇.试问两人的速度各是多少?
意图:引导学生解决行程问题时,借助示意图表示题中的数量关系,这样可以更加直观的找到相等关系.
效果:培养学生运用方程组解决行程问题的能力.
(三)当堂练习
1.有甲、乙两数,甲数的3倍与乙数的2倍之和等于47,甲数的5倍比乙数的6倍小1,这两个数分别是多少?
2.某船顺流航行36km用3 h,逆流航行24km用3 h,则水流速度和船在静水中的速度各是多少?
意图:感受数学在生活中的广泛应用,检测本节课所学知识.
效果:巩固知识,强化练习.
(四)课堂小结
(五)作业布置
完成配套作业
六、板书设计
8.3.1实际问题与二元一次方程组
七、课后反思
本节课的重点是让学生经历和体验用方程组解决实际问题的过程,抓住实际问题的等量关系建立方程组模型.教学难点是利用相等关系将实际问题转化为数学问题.教学中,采取了让学生通过独立思考、自主探索、合作交流等方式,在思考、交流等数学活动中,养成严谨的思维方式和良好的学习习惯.
意图:先让学生自己总结反思,总结反思是一节课必不可少的环节,有助于学生巩固所学,并检验自己不懂的地方是否弄明白.
1
一、教材分析
《实际问题与二元一次方程组》是人民教育出版社七年级(下)第八章《二元一次方程组》第三节.本节内容安排了2个课时完成,是在学生掌握了二元一次方程组的解法,能列二元一次方程组解较简单的实际问题的基础上安排的,其中的“和差倍分问题”“几何问题”“行程问题”是具有一定综合性的问题.本课时选择了两个且有一定综合性的问题,“牛饲料问题”“种植计划问题”.让学生以方程组为工具进行一定深度的思考,丰富运用方程组解决实际问题的实践,把本章强调的以方程组为工具,实际问题模型化的思想提到新的高度.为切实提高利用方程组解决实际问题的能力,这节内容的问题形式包括,估算与精确计算的比较(探究1),开放地寻求设计方案(探究2),本节目的在于,一方面通过实际生活中的问题,进一步突出方程组这种数学模型应用的广泛性和有效性;另一方面使学生在实际问题情境中运用所学数学知识,进一步提高分析问题和解决问题的能力.
二、教学目标
1.学会利用二元一次方程组解决和、差、倍、分问题,几何问题和行程问题.
2.经历探索用二元一次方程组解决实际问题的过程,进一步提高分析问题中数量关系、设未知数、列方程组、解方程组的能力,体会数学建模思想.
三、教学重难点
【重点】会利用二元一次方程组解决和、差、倍、分问题,几何问题和行程问题.
【难点】正确找出问题中的两个等量关系,体会数学建模思想.
四、教学方法
探究式学习法、讲练结合法.
五、教学过程
(一)新课导入
视频导入
多媒体播放《奔跑吧,兄弟》的某段视频,引出“鸡兔同笼问题”,问:视频中的问题你知道怎么解吗?
意图:以视频方式引出二元一次方程组可以顺利解决“鸡兔同笼问题”.让学生充分表达自己的想法,部分学生可能用算数的方法,也可能用方程组,学生初步感知算数和方程组解决实际问题的异同,发现方程组和方程是数学的进步.
效果:通过视频导入这个环节,激发了学生本节课的学习兴趣,活跃了课堂氛围.以熟悉的问题为背景,让学生感受到这节课并不陌生,让学生有种亲切感,更易于接受新的概念,对本节课的学习增强了信心.
(二)探究新知
1.列方程组解决和、差、倍、分问题
出示教材的探究1
养牛场原有30只大牛和15只小牛,1天约用饲料675 kg;一周后又购进12只大牛和5只小牛,这时1天约用饲料940 kg.饲养员李大叔估计每只大牛1天约需饲料18到20 kg,每只小牛1天约需饲料7到8 kg.你认为李大叔估计的准确吗?
教师出示两个问题:
问题1 如何理解“通过计算检验他的估计”这句话?
问题2 题目中有哪些未知量?你如何设未知数?题目中有哪些等量关系?
(学生自由发言)
意图:教师提出两个问题,问题1让学生体会对于估算的结果要通过精确求职来检验,理解要想检验估计是否准确,需要求出大牛、小牛1天所需要的饲料;问题2重在引导学生发现问题中的已知量和未知量,寻找等量关系,借助二元一次方程组进行计算.
效果:学生独立探究,合作交流.让学生学会分析问题中的数量关系,发现等量关系,体会数学建模的关键过程.
问题3 如何解决这个问题?
学生依据发现的等量关系,建立方程组.
设每头大牛和小牛平均1天各需用饲料为x kg和y kg,根据等量关系,列方程组:
追问:你是如何解这个方程组的?列一元一次方程能解决这个问题吗?
意图:学生独立解方程组,并发言交流.让学生经历分析数量关系,得到数量关系,列方程组的过程.一般情况下,学生会自觉选择列方程组解决.
效果:学生通过交流对比发现,由实际问题列出的方程组,有时系数较为复杂,先化简再求解,可以简化运算.学生体会到有两个未知量时列方程组更为简单.
出示剧情发展:随着养牛场规模逐渐扩大,李大叔需聘请饲养员协助管理现有的42头大牛和20头小牛,已知甲种饲养员每人可负责8头大牛和4头小牛,乙种饲养员每人可负责5头大牛和2头小牛,请问李大叔应聘请甲乙两种饲养员各多少人?
总结归纳:
用二元一次方程组解决实际问题的步骤:
(1)审题:弄清题意和题目中的 数量关系;
(2)设元:用 字母 表示题目中的未知数;
(3)列方程组:根据 2 个等量关系列出方程组;
(4)解方程组:利用 代入消元 法或 加减消元 法解出未知数的值;
(5)检验并答:检验所求的解是否符合实际意义,然后作答.
意图:学生在解决探究1的基础上继续探究,独立思考,运用二元一次方程组解决该问题.并总结用二元一次方程组解决实际问题的一般步骤.
效果:学生能够准确分析该问题的已知量和未知量,并运用二元一次方程组解决该问题,使知识得以强化.并提升总结归纳的能力.
针对练习1:
例1 某市举办中学生足球比赛,规定胜一场得3分,平一场得1分.市第二中学足球队比赛11场,没有输过一场,共得27分,试问该队胜几场,平几场?
意图:用方程组解决生活情景“球赛积分问题”,体会用一元一次方程和二元一次方程组解决实际问题的区别与练习.
效果:学生能够熟练运用二元一次方程组解决该问题,提高了学生解决实际问题的能力.
2.列方程组解决几何问题
出示探究2
据统计资料,甲、乙两种作物的单位面积产量的比是1:2.现要把一块长200m、宽100m的长方形土地,分为两块小长方形土地,分别种植这两种作物.怎样划分这块土地,使甲、乙两种作物的总产量的比是3:4?
你能设计出种植方案吗?你能从中提取出数学信息吗?请你画出图形,结合上面的框图以及“探究1”的解决过程,如何解决探究2中的问题?
(学生独立思考,互相讨论交流,有一定难度,进行追问)
追问:这里研究的实际上是长方形的面积分割问题,有几种分割方式?请将文字语言转换成数学语言.
转换成数学语言:
已知:长方形ABCD, AB=CD=200m,AD=BC=100m,长方形ABCD分割为两个小长方形,长方形1和长方形2分别种植甲、乙作物,甲、乙单位面积产量的比是1:2.
(学生思考回答)
(1)竖着画,把长分成两段,则宽不变;
(2)横着画,把宽分成两段,则长不变.
学生画图分析题意,上板写出解题过程,并进行解析.
意图:让学生经历列方程组解决实际问题的完整过程,一题多解,体现思维的多样性.效果:学生互相交流,互相启发,不断完善种植方案,经历列方程组解决实际问题的过程,加深对建模一般步骤的理解.
针对练习2
8块相同的小长方形地砖拼成一个大长方形,每块小长方形地砖的长和宽分别是多少?(单位cm)
解析:
直接设:小长方形地砖的长为x, 宽为y.
等量关系为:
(小长方形的一个长)+(小长方形的一个宽)= 大长方形的宽60;
小长方形的长 = 小长方形3个宽.
学生观察图形,发现几何拼图中隐藏的等量关系,列出方程组求解.
意图:对探究2作针对练习,用方程组解决几何中的拼图问题.
效果:培养学生的观察能力,应用方程组解决几何问题的能力.
3.列方程组解决行程问题
探究3
小华从家里到学校的路是一段平路和一段下坡路. 假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问小华家离学校多远?
通过画线段图的方法表示从家到学校的路途,分析往返途中的两个等量关系,列方程组.
等量关系:从家里到学校:走平路的时间+走下坡路的时间= 10 ;
从学校到家里:走上坡路的时间+走平路的时间= 15 .
方法一(直接设元法)
解:设小华家到学校平路长x m,下坡路长y m.
根据题意,可列方程组:
解方程组,得
所以,x+y=300+400=700.
答:小明家到学校的距离为700m.
方法二(间接设元法)
解:设小华下坡路所花时间为x min,上坡路所花时间为y min.
根据题意,可列方程组:
解方程组,得
所以坡路距离:80×5=400(m),平路距离:60×(10-5)=300(m)
所以,小明家到学校的距离为700m.
意图:遇到行程问题,经常会设不同的未知数,让学生大胆尝试,感受直接设元和间接设元的不同.
效果:用画线段图和列表的方法,来减小坡度、分散难点,另一方面利用画图来引导学生学会分析和表达.
针对练习3
例2 甲、乙两人相距4km,以各自的速度同时出发.如果同向而行,甲2h追上乙;如果相向而行,两人0.5h后相遇.试问两人的速度各是多少?
意图:引导学生解决行程问题时,借助示意图表示题中的数量关系,这样可以更加直观的找到相等关系.
效果:培养学生运用方程组解决行程问题的能力.
(三)当堂练习
1.有甲、乙两数,甲数的3倍与乙数的2倍之和等于47,甲数的5倍比乙数的6倍小1,这两个数分别是多少?
2.某船顺流航行36km用3 h,逆流航行24km用3 h,则水流速度和船在静水中的速度各是多少?
意图:感受数学在生活中的广泛应用,检测本节课所学知识.
效果:巩固知识,强化练习.
(四)课堂小结
(五)作业布置
完成配套作业
六、板书设计
8.3.1实际问题与二元一次方程组
七、课后反思
本节课的重点是让学生经历和体验用方程组解决实际问题的过程,抓住实际问题的等量关系建立方程组模型.教学难点是利用相等关系将实际问题转化为数学问题.教学中,采取了让学生通过独立思考、自主探索、合作交流等方式,在思考、交流等数学活动中,养成严谨的思维方式和良好的学习习惯.
意图:先让学生自己总结反思,总结反思是一节课必不可少的环节,有助于学生巩固所学,并检验自己不懂的地方是否弄明白.
1
