初中数学人教版七下6.2立方根 教案
图片预览


文档简介
6.2立方根
一、教材分析
《立方根》是人民教育出版社七年级(下)第六章《实数》第二节.本节内容安排了1个学时完成.主要是通过对立方根与平方根的比较与归类,探索立方根的概念、计算和性质.因此,除了具体的知识技能(如知道一个数的立方根的意义,会用根号表示一个数的立方根,学握立方根运算,学握求一个数的立方根的方法和技巧)外,还需要学生感受类比的思想方法,为今后的学习打下基础.
二、教学目标
1.理解立方根的概念,会表示一个数的立方根,并会求一个数的立方根,了解开立方与立方互为逆运算.
2.掌握立方根的性质,能区分立方根与平方根的不同.通过类比平方根学习立方根,体会类比思想的运用.
3.会用计算器计算一个数的立方根或立方根的近似值.
三、教学重难点
【重点】正确地理解立方根的概念,会用开立方运算求一个数的立方根.
【难点】立方根和平方根的区别.
四、教学方法
自主探究式学习法.
五、教学过程
(一)新课导入
1.复习导入
多媒体出示两个问题,问:
你还记得什么是平方根吗?平方根具有什么特征?
意图:通过复习平方根的概念和特征引入立方根的概念和特征.
效果:让学生初步体会类比思想的应用.
2.情景导入
如图,要制作一个容积为27cm3的正方体包装箱,它的棱长是多少?
意图:从实际生活中的情景出发,导入本节课内容,让学生了解到数学来源于生活,又应用于生活.
效果:让学生有种亲切感,更易于接受新的概念,不产生陌生感.
(二)探究新知
1.立方根的概念
类比:回忆上节课学方根的概念和符号表示方法,引导学生自己归纳出立方根的概念和符号表示.
立方根定义:一般地,如果一个数的立方等于a,那么这个数叫作a的立方根,或三次方根.这就是说,如果x3=a,那么x叫做a的立方根(或三次方根).
2.立方根符号表示:类似于平方根,一个数a的立方根,用符号“ ”表示,读作:“三次根号a ”,其中a叫做被开方数,3叫做根指数.
意图:通过自己已掌握的知识去探究新知,了解知识之间的相互联系和区别,促使学生进行主动的知识建构.
效果:通过类比平方根学习立方根,体会类比思想的运用.
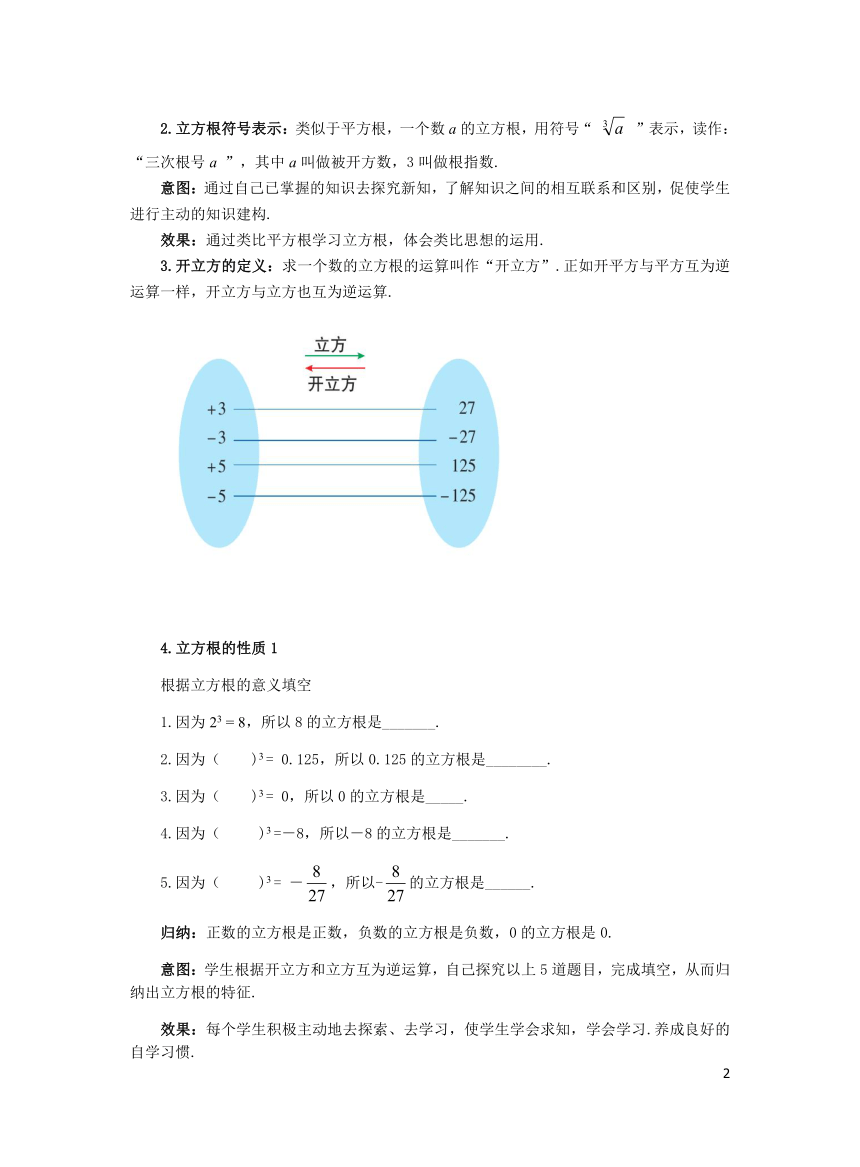
3.开立方的定义:求一个数的立方根的运算叫作“开立方”.正如开平方与平方互为逆运算一样,开立方与立方也互为逆运算.
4.立方根的性质1
根据立方根的意义填空
1.因为23 = 8,所以8的立方根是_______.
2.因为( )3 = 0.125,所以0.125的立方根是________.
3.因为( )3 = 0,所以0的立方根是_____.
4.因为( )3 =-8,所以-8的立方根是_______.
5.因为( )3 = -,所以-的立方根是______.
归纳:正数的立方根是正数,负数的立方根是负数,0的立方根是0.
意图:学生根据开立方和立方互为逆运算,自己探究以上5道题目,完成填空,从而归纳出立方根的特征.
效果:每个学生积极主动地去探索、去学习,使学生学会求知,学会学习.养成良好的自学习惯.
5.平方根与立方根的区别和联系
对应练习:小活动“轻松写意” —— 选一选,你能做对吗?
意图:学生通过小组交流,总结归纳平方根和立方根的区别.突出学生的主体地位,培养主动参与的意识,激发学生的创造潜能.并通过一个对应小练习,掌握平方根和立方根的区别.
效果:营造轻松、活泼而又团结互助的学习环境,有利于学生间的彼此了解,培养合作能力和团队精神.
6.立方根的性质2
因为 ,-= ,所以 - ;
因为= ,-= ,所以 -.
归纳:.
意图:学生通过计算、探究、观察、总结出立方根的性质.
(三)课堂练习一
例1. 的算术平方根是 .
解析:= 4;4的算术平方根是2.
例2.分别求下列各式的值:
(1) (2) (3)
解析:= -7 ;= ;= .
例3.计算:
解析:原式=3+2-(-1) = 5+1 = 6.
活动:PK赛
1.快速说出1-10的立方(个人赛,规则:准确无误,时间少者获胜).
2.你来出题我来答(小组赛,以抽签的方式对战.一个小组在卡片上任意出题,邀请另一小组对战.题目自拟,形式可以是填空,也可以是“判断对错”等多种形式,出题范围要与本节内容相关).
意图:通过活动使学生熟练掌握10以内的数的立方,以学生出题学生答的模式帮助记忆,提高平常的做题速度,激发学生的求知欲.
7.探究:利用计算器求立方根
用计算器求下列各数的立方根:343,-1.331.
解:依次按键:
显示:7
依次按键:
显示:-1.1
= -1.1
意图:加强学生的动手操作能力.
用计算器计算,,,,,...,你能发现什么规律?
= 0.06,= 0.6,= 6,= 60
规律:被开方数的小数点向左或向右移动3n位时,立方根的小数点就相应的向左或向右移动n位(n为正整数).
用你发现的规律填空:
已知,≈4.642,
则 = ,= , = .
课堂互动
“知识配对”
意图:通过课堂互动,使学生能够熟练地求出一个数的立方根,提高学生的专注度,增强学生的学习兴趣,活跃课堂气氛.
课堂练习二
基础巩固
1.求下列式中x的值.
(1)x3=0.008; (2)(x-1)3=27.
解析:(1)x=
∴ x = 0.2 ;
(2)x-1=
∴ x = 3+1=4
能力提升
2.已知x+3的平方根是,x-y 的立方根是 2, 求x+y的算术平方根.
解析:由平方根、立方根的概念得
x+3 =(3)2 = 9
x-y=23 = 8
解得x = 6,y = -2.
∴
拓展练习
3.若
解析:由
∴2x+1+2x-5 = 0
4x = 4
解得x=1.
意图:采用分层练习,使知识层层深入,便于知识的灵活运用,同时达到检测和巩固本节所学知识的目的.
(四)课堂小结
意图:先让学生自己总结反思,总结反思是一节课必不可少的环节,有助于学生巩固所学,并检验自己不懂的地方是否弄明白. 然后再通过一个小微课梳理本节课的重点和思路.
(五)作业布置
完成配套作业
六、板书设计
6.2立方根
1.立方根的概念 4.立方根的特征:①、②、③
2.数学符号表示 5.立方根的性质:
3.开立方与立方互为逆运算
七、课后反思
本节课采取自主探究式学习法,促使学生进行主动的知识建构,培养其自主学习的能力;让学生应用类比的学习方法学习立方根的概念、性质和运算.学生在以后的数学学习中,要注意渗透类比的思维方式,让学生在学习新知识的同时巩固已学的知识,并通过新旧对比更好地掌握知识.
1
一、教材分析
《立方根》是人民教育出版社七年级(下)第六章《实数》第二节.本节内容安排了1个学时完成.主要是通过对立方根与平方根的比较与归类,探索立方根的概念、计算和性质.因此,除了具体的知识技能(如知道一个数的立方根的意义,会用根号表示一个数的立方根,学握立方根运算,学握求一个数的立方根的方法和技巧)外,还需要学生感受类比的思想方法,为今后的学习打下基础.
二、教学目标
1.理解立方根的概念,会表示一个数的立方根,并会求一个数的立方根,了解开立方与立方互为逆运算.
2.掌握立方根的性质,能区分立方根与平方根的不同.通过类比平方根学习立方根,体会类比思想的运用.
3.会用计算器计算一个数的立方根或立方根的近似值.
三、教学重难点
【重点】正确地理解立方根的概念,会用开立方运算求一个数的立方根.
【难点】立方根和平方根的区别.
四、教学方法
自主探究式学习法.
五、教学过程
(一)新课导入
1.复习导入
多媒体出示两个问题,问:
你还记得什么是平方根吗?平方根具有什么特征?
意图:通过复习平方根的概念和特征引入立方根的概念和特征.
效果:让学生初步体会类比思想的应用.
2.情景导入
如图,要制作一个容积为27cm3的正方体包装箱,它的棱长是多少?
意图:从实际生活中的情景出发,导入本节课内容,让学生了解到数学来源于生活,又应用于生活.
效果:让学生有种亲切感,更易于接受新的概念,不产生陌生感.
(二)探究新知
1.立方根的概念
类比:回忆上节课学方根的概念和符号表示方法,引导学生自己归纳出立方根的概念和符号表示.
立方根定义:一般地,如果一个数的立方等于a,那么这个数叫作a的立方根,或三次方根.这就是说,如果x3=a,那么x叫做a的立方根(或三次方根).
2.立方根符号表示:类似于平方根,一个数a的立方根,用符号“ ”表示,读作:“三次根号a ”,其中a叫做被开方数,3叫做根指数.
意图:通过自己已掌握的知识去探究新知,了解知识之间的相互联系和区别,促使学生进行主动的知识建构.
效果:通过类比平方根学习立方根,体会类比思想的运用.
3.开立方的定义:求一个数的立方根的运算叫作“开立方”.正如开平方与平方互为逆运算一样,开立方与立方也互为逆运算.
4.立方根的性质1
根据立方根的意义填空
1.因为23 = 8,所以8的立方根是_______.
2.因为( )3 = 0.125,所以0.125的立方根是________.
3.因为( )3 = 0,所以0的立方根是_____.
4.因为( )3 =-8,所以-8的立方根是_______.
5.因为( )3 = -,所以-的立方根是______.
归纳:正数的立方根是正数,负数的立方根是负数,0的立方根是0.
意图:学生根据开立方和立方互为逆运算,自己探究以上5道题目,完成填空,从而归纳出立方根的特征.
效果:每个学生积极主动地去探索、去学习,使学生学会求知,学会学习.养成良好的自学习惯.
5.平方根与立方根的区别和联系
对应练习:小活动“轻松写意” —— 选一选,你能做对吗?
意图:学生通过小组交流,总结归纳平方根和立方根的区别.突出学生的主体地位,培养主动参与的意识,激发学生的创造潜能.并通过一个对应小练习,掌握平方根和立方根的区别.
效果:营造轻松、活泼而又团结互助的学习环境,有利于学生间的彼此了解,培养合作能力和团队精神.
6.立方根的性质2
因为 ,-= ,所以 - ;
因为= ,-= ,所以 -.
归纳:.
意图:学生通过计算、探究、观察、总结出立方根的性质.
(三)课堂练习一
例1. 的算术平方根是 .
解析:= 4;4的算术平方根是2.
例2.分别求下列各式的值:
(1) (2) (3)
解析:= -7 ;= ;= .
例3.计算:
解析:原式=3+2-(-1) = 5+1 = 6.
活动:PK赛
1.快速说出1-10的立方(个人赛,规则:准确无误,时间少者获胜).
2.你来出题我来答(小组赛,以抽签的方式对战.一个小组在卡片上任意出题,邀请另一小组对战.题目自拟,形式可以是填空,也可以是“判断对错”等多种形式,出题范围要与本节内容相关).
意图:通过活动使学生熟练掌握10以内的数的立方,以学生出题学生答的模式帮助记忆,提高平常的做题速度,激发学生的求知欲.
7.探究:利用计算器求立方根
用计算器求下列各数的立方根:343,-1.331.
解:依次按键:
显示:7
依次按键:
显示:-1.1
= -1.1
意图:加强学生的动手操作能力.
用计算器计算,,,,,...,你能发现什么规律?
= 0.06,= 0.6,= 6,= 60
规律:被开方数的小数点向左或向右移动3n位时,立方根的小数点就相应的向左或向右移动n位(n为正整数).
用你发现的规律填空:
已知,≈4.642,
则 = ,= , = .
课堂互动
“知识配对”
意图:通过课堂互动,使学生能够熟练地求出一个数的立方根,提高学生的专注度,增强学生的学习兴趣,活跃课堂气氛.
课堂练习二
基础巩固
1.求下列式中x的值.
(1)x3=0.008; (2)(x-1)3=27.
解析:(1)x=
∴ x = 0.2 ;
(2)x-1=
∴ x = 3+1=4
能力提升
2.已知x+3的平方根是,x-y 的立方根是 2, 求x+y的算术平方根.
解析:由平方根、立方根的概念得
x+3 =(3)2 = 9
x-y=23 = 8
解得x = 6,y = -2.
∴
拓展练习
3.若
解析:由
∴2x+1+2x-5 = 0
4x = 4
解得x=1.
意图:采用分层练习,使知识层层深入,便于知识的灵活运用,同时达到检测和巩固本节所学知识的目的.
(四)课堂小结
意图:先让学生自己总结反思,总结反思是一节课必不可少的环节,有助于学生巩固所学,并检验自己不懂的地方是否弄明白. 然后再通过一个小微课梳理本节课的重点和思路.
(五)作业布置
完成配套作业
六、板书设计
6.2立方根
1.立方根的概念 4.立方根的特征:①、②、③
2.数学符号表示 5.立方根的性质:
3.开立方与立方互为逆运算
七、课后反思
本节课采取自主探究式学习法,促使学生进行主动的知识建构,培养其自主学习的能力;让学生应用类比的学习方法学习立方根的概念、性质和运算.学生在以后的数学学习中,要注意渗透类比的思维方式,让学生在学习新知识的同时巩固已学的知识,并通过新旧对比更好地掌握知识.
1
