23.1.2平行线分线段成比例 课件(共28张PPT)
文档属性
| 名称 | 23.1.2平行线分线段成比例 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 328.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-23 09:03:59 | ||
图片预览


文档简介
(共28张PPT)
23.1 平行线分线段成比例
****初级中学 ***
知识目标:掌握平行线分线段成比例及推论并能用其解题.
能力目标:掌握基本事实的推导过程并能以之解题.
情感目标:培养认识事物从一般到特殊的认识过程,培养欣赏 数学表达式的对称美
教学目标
重点:平行线分线段成比例及其推论.
难点:灵活运用基本事实及推论.
教学重难点
(一)根据目标及重、难点自主预习书
P51-54
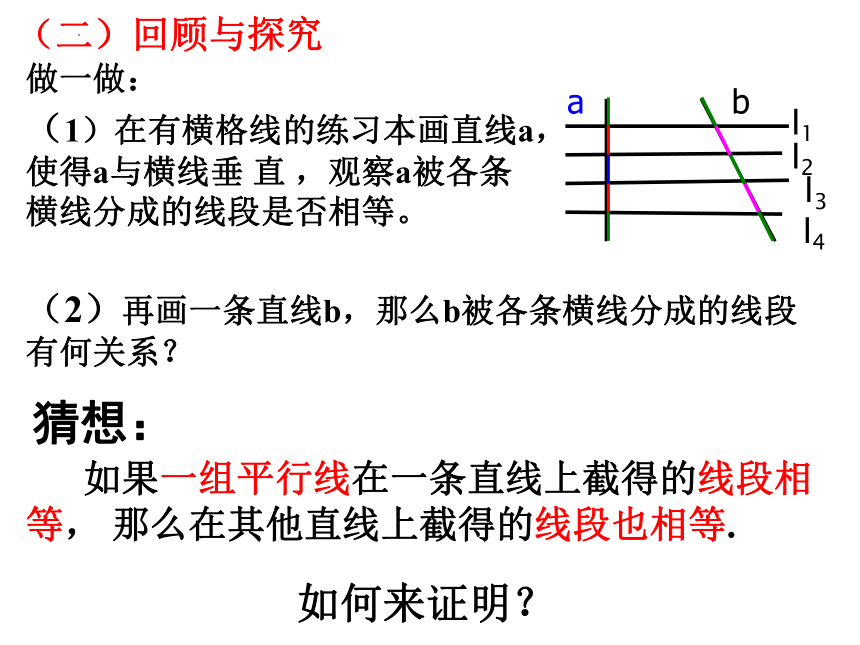
做一做:
(1)在有横格线的练习本画直线a,使得a与横线垂 直 ,观察a被各条横线分成的线段是否相等。
(2)再画一条直线b,那么b被各条横线分成的线段有何关系?
a
b
如果一组平行线在一条直线上截得的线段相等, 那么在其他直线上截得的线段也相等.
猜想:
如何来证明?
l1
l2
l3
l4
(二)回顾与探究
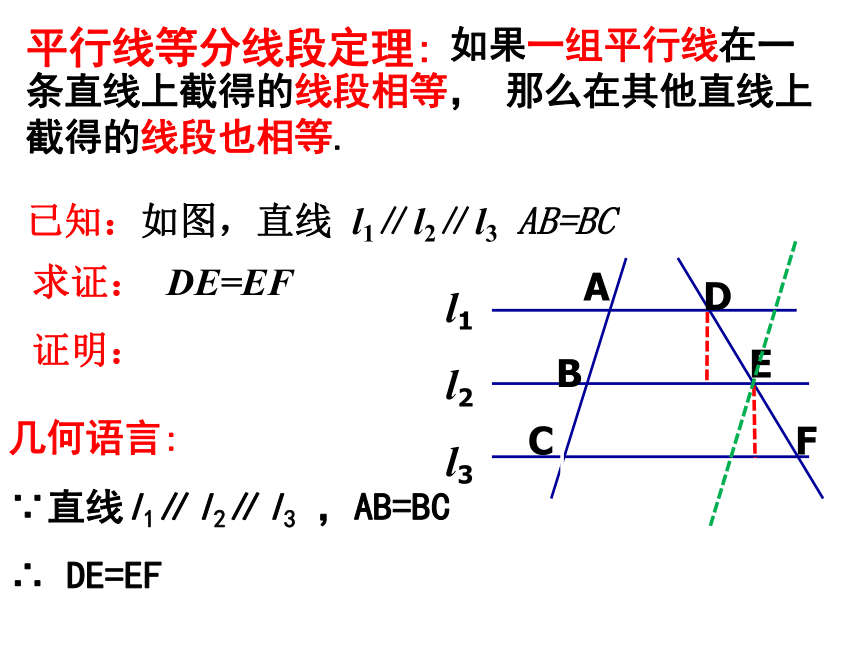
已知:如图,直线 l1∥l2∥l3 AB=BC
平行线等分线段定理:
求证: DE=EF
证明:
如果一组平行线在一条直线上截得的线段相等, 那么在其他直线上截得的线段也相等.
A
B
C
D
E
F
l1
l3
l2
几何语言:
∵直线l1∥l2∥l3 ,AB=BC
∴ DE=EF
A
B
C
D
E
F
l1
l3
l2
上
下
上
下
=
上
全
上
全
=
下
全
下
全
=
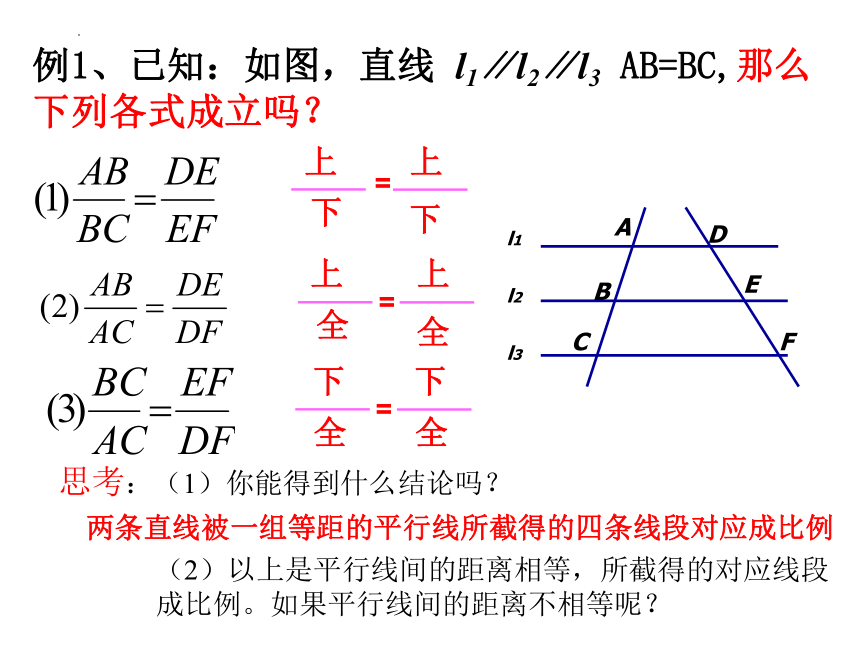
例1、已知:如图,直线 l1∥l2∥l3 AB=BC,那么下列各式成立吗?
思考:(1)你能得到什么结论吗?
两条直线被一组等距的平行线所截得的四条线段对应成比例
(2)以上是平行线间的距离相等,所截得的对应线段
成比例。如果平行线间的距离不相等呢?
A
B
C
D
E
F
a
b
L1
L2
L4
L3
上
下
上
下
=
上
全
上
全
=
下
全
下
全
=
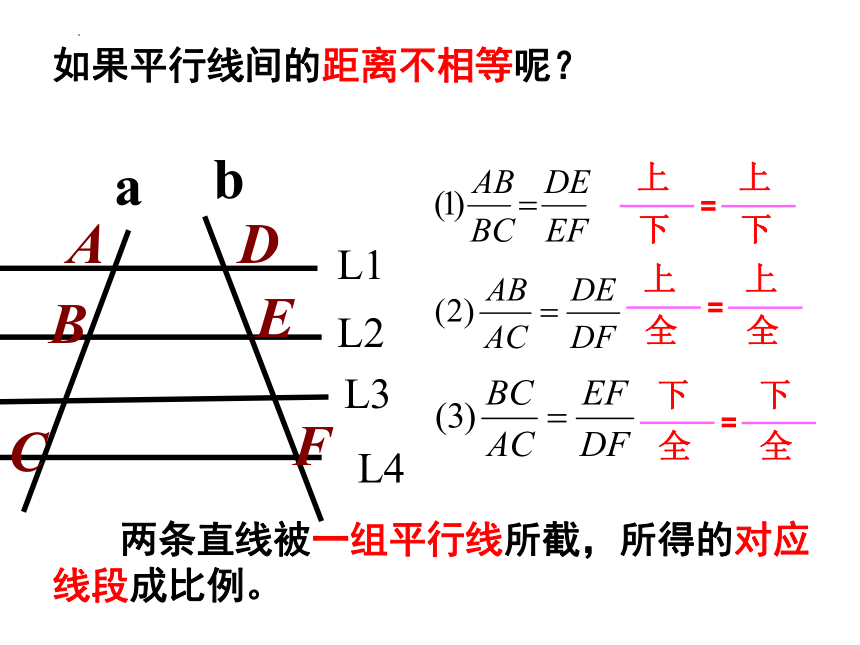
如果平行线间的距离不相等呢?
两条直线被一组平行线所截,所得的对应线段成比例。
L1//L2//L3
=
AB
DE
BC
EF
(平行线分线段成比例)
D
E
F
A
B
C
L1
L2
L3
a
b
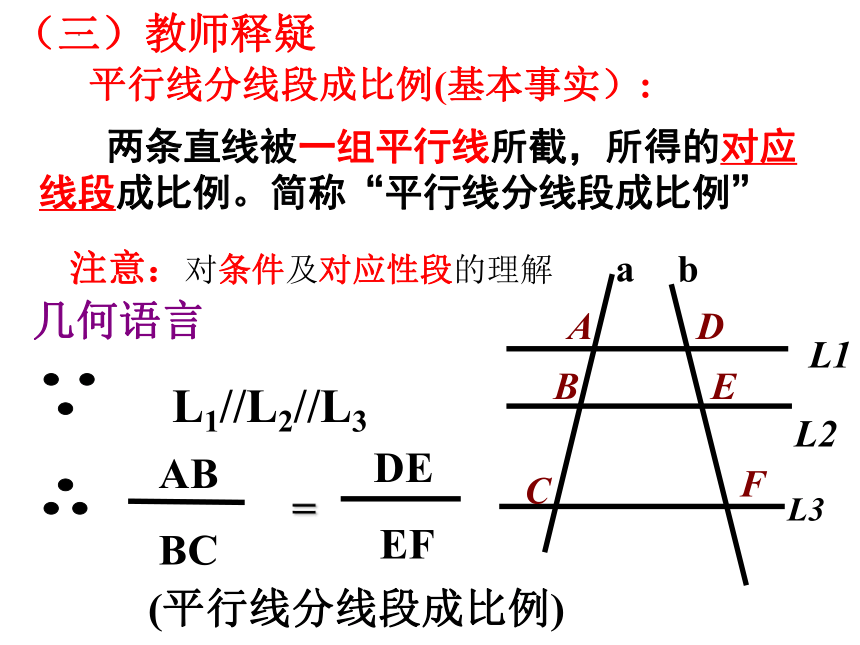
两条直线被一组平行线所截,所得的对应线段成比例。简称“平行线分线段成比例”
几何语言
平行线分线段成比例(基本事实):
注意:对条件及对应性段的理解
(三)教师释疑
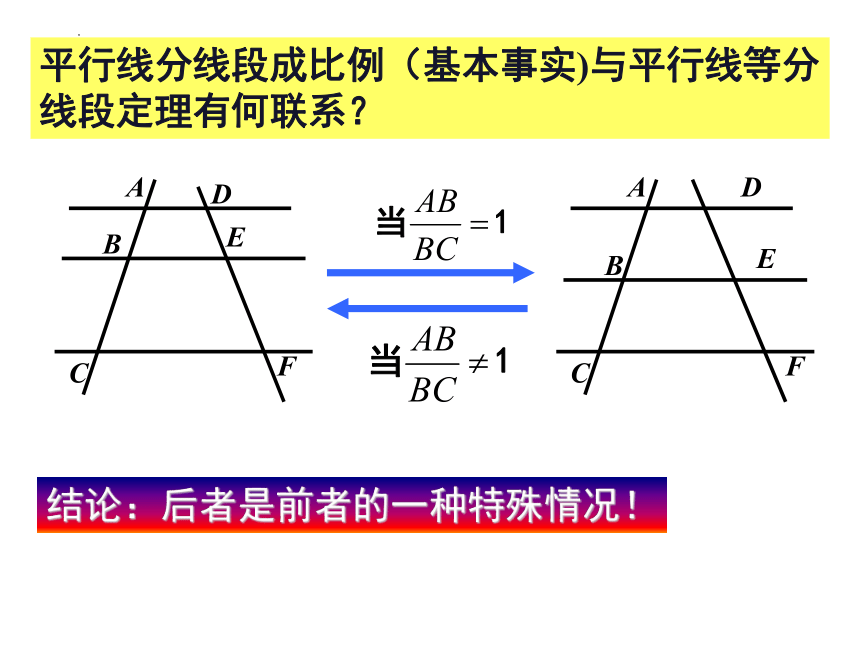
平行线分线段成比例(基本事实)与平行线等分线段定理有何联系?
A
B
C
D
E
F
A
B
C
D
E
F
结论:后者是前者的一种特殊情况!
A
B
C
D
E
F
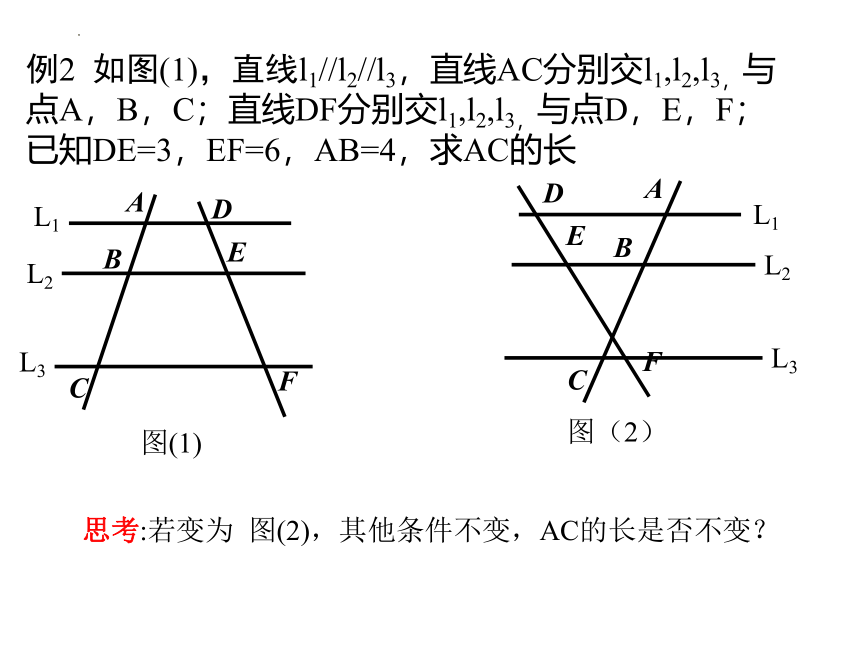
例2 如图(1),直线l1//l2//l3,直线AC分别交l1,l2,l3,与点A,B,C;直线DF分别交l1,l2,l3,与点D,E,F;
已知DE=3,EF=6,AB=4,求AC的长
A
B
C
D
E
F
图(1)
图(2)
思考:若变为 图(2),其他条件不变,AC的长是否不变?
L1
L2
L3
L1
L2
L3
L1
L2
L3
a
b
L1
L2
L3
a
b
L1
L2
L3
a
b
L1
L2
L3
a
b
L4
L5
L1
L2
L3
A
B
C
D
E
A字形
L1
L2
L3
a
b
L1
L2
L3
a
b
L4
L5
L1
L2
L3
L4
L5
L1
L2
L3
E
A
B
D
C
8字形
推论:
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
几何语言:
∵ DE∥BC
AD AE
AB AC
∴
——
——
=
(推论)
A
B
C
D
E
A
B
C
E
D
这两个图形是以后解决相似三角形的有关计算和证明的
模具,以后我们会经常构造或寻找A字型或8字型解决问题.
例3.如图,DE∥AF∥BC,根据上面结论,试找出图中成比例的线(教材P53)ABCDEFABCEFACDEFABCDE分解基本图形2.已知两条直线被三条平行线所截,截得线段的长度如
图所示,则m= .
四、构建知识体系
课堂练习(一):
3.如图,在△ABC中,MN∥BC,则
BM∶CN=AM∶ ,
AB∶AM= ∶AN.
4.如图,在△ABC中,DE∥BC,则下列等式中不成立的是( )
A. AD∶AB=AE∶AC
B. AD∶DB=AE∶EC
C. AD∶DB=DE∶BC
D. BD∶AB=CE∶AC
5.如图,已知ED∥BC.AB=3,AC=4,AD=2,则
EC=____.
6.已知:AB与CD相交于点E,BC//EF//AD,
E
D
A
B
C
F
课堂练习(二)
1、如图,已知在△ABC中,点D,E,F分别是边AB,AC,BC上
的点,DE∥BC,EF∥AB,且AD∶DB=3∶5,那么CF∶CB等于 ( )2
1A.5∶8 B.3∶8 C.3∶5 D.2∶5
世纪教育网版权所有
2.如图,△ABC中,DE//BC,DF//AC,AE=4,EC=2,BC=8.求BF和CF的长.FACB分析:运用平行线分线段成比例定理的推论分别列出比例式求解.解∵DE//BC∵DF//ACDE说说你在这节课中的收获与体会
小结:
五、分层布置作业
A: 探究从书 P54-P55
B: 探究练习
F
BF=DE
探究作业
DE
23.1 平行线分线段成比例
****初级中学 ***
知识目标:掌握平行线分线段成比例及推论并能用其解题.
能力目标:掌握基本事实的推导过程并能以之解题.
情感目标:培养认识事物从一般到特殊的认识过程,培养欣赏 数学表达式的对称美
教学目标
重点:平行线分线段成比例及其推论.
难点:灵活运用基本事实及推论.
教学重难点
(一)根据目标及重、难点自主预习书
P51-54
做一做:
(1)在有横格线的练习本画直线a,使得a与横线垂 直 ,观察a被各条横线分成的线段是否相等。
(2)再画一条直线b,那么b被各条横线分成的线段有何关系?
a
b
如果一组平行线在一条直线上截得的线段相等, 那么在其他直线上截得的线段也相等.
猜想:
如何来证明?
l1
l2
l3
l4
(二)回顾与探究
已知:如图,直线 l1∥l2∥l3 AB=BC
平行线等分线段定理:
求证: DE=EF
证明:
如果一组平行线在一条直线上截得的线段相等, 那么在其他直线上截得的线段也相等.
A
B
C
D
E
F
l1
l3
l2
几何语言:
∵直线l1∥l2∥l3 ,AB=BC
∴ DE=EF
A
B
C
D
E
F
l1
l3
l2
上
下
上
下
=
上
全
上
全
=
下
全
下
全
=
例1、已知:如图,直线 l1∥l2∥l3 AB=BC,那么下列各式成立吗?
思考:(1)你能得到什么结论吗?
两条直线被一组等距的平行线所截得的四条线段对应成比例
(2)以上是平行线间的距离相等,所截得的对应线段
成比例。如果平行线间的距离不相等呢?
A
B
C
D
E
F
a
b
L1
L2
L4
L3
上
下
上
下
=
上
全
上
全
=
下
全
下
全
=
如果平行线间的距离不相等呢?
两条直线被一组平行线所截,所得的对应线段成比例。
L1//L2//L3
=
AB
DE
BC
EF
(平行线分线段成比例)
D
E
F
A
B
C
L1
L2
L3
a
b
两条直线被一组平行线所截,所得的对应线段成比例。简称“平行线分线段成比例”
几何语言
平行线分线段成比例(基本事实):
注意:对条件及对应性段的理解
(三)教师释疑
平行线分线段成比例(基本事实)与平行线等分线段定理有何联系?
A
B
C
D
E
F
A
B
C
D
E
F
结论:后者是前者的一种特殊情况!
A
B
C
D
E
F
例2 如图(1),直线l1//l2//l3,直线AC分别交l1,l2,l3,与点A,B,C;直线DF分别交l1,l2,l3,与点D,E,F;
已知DE=3,EF=6,AB=4,求AC的长
A
B
C
D
E
F
图(1)
图(2)
思考:若变为 图(2),其他条件不变,AC的长是否不变?
L1
L2
L3
L1
L2
L3
L1
L2
L3
a
b
L1
L2
L3
a
b
L1
L2
L3
a
b
L1
L2
L3
a
b
L4
L5
L1
L2
L3
A
B
C
D
E
A字形
L1
L2
L3
a
b
L1
L2
L3
a
b
L4
L5
L1
L2
L3
L4
L5
L1
L2
L3
E
A
B
D
C
8字形
推论:
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
几何语言:
∵ DE∥BC
AD AE
AB AC
∴
——
——
=
(推论)
A
B
C
D
E
A
B
C
E
D
这两个图形是以后解决相似三角形的有关计算和证明的
模具,以后我们会经常构造或寻找A字型或8字型解决问题.
例3.如图,DE∥AF∥BC,根据上面结论,试找出图中成比例的线(教材P53)ABCDEFABCEFACDEFABCDE分解基本图形2.已知两条直线被三条平行线所截,截得线段的长度如
图所示,则m= .
四、构建知识体系
课堂练习(一):
3.如图,在△ABC中,MN∥BC,则
BM∶CN=AM∶ ,
AB∶AM= ∶AN.
4.如图,在△ABC中,DE∥BC,则下列等式中不成立的是( )
A. AD∶AB=AE∶AC
B. AD∶DB=AE∶EC
C. AD∶DB=DE∶BC
D. BD∶AB=CE∶AC
5.如图,已知ED∥BC.AB=3,AC=4,AD=2,则
EC=____.
6.已知:AB与CD相交于点E,BC//EF//AD,
E
D
A
B
C
F
课堂练习(二)
1、如图,已知在△ABC中,点D,E,F分别是边AB,AC,BC上
的点,DE∥BC,EF∥AB,且AD∶DB=3∶5,那么CF∶CB等于 ( )2
1A.5∶8 B.3∶8 C.3∶5 D.2∶5
世纪教育网版权所有
2.如图,△ABC中,DE//BC,DF//AC,AE=4,EC=2,BC=8.求BF和CF的长.FACB分析:运用平行线分线段成比例定理的推论分别列出比例式求解.解∵DE//BC∵DF//ACDE说说你在这节课中的收获与体会
小结:
五、分层布置作业
A: 探究从书 P54-P55
B: 探究练习
F
BF=DE
探究作业
DE
