3.3 圆周角和圆心角的关系(1)(广东省深圳市)
文档属性
| 名称 | 3.3 圆周角和圆心角的关系(1)(广东省深圳市) |  | |
| 格式 | rar | ||
| 文件大小 | 368.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-01-10 06:47:00 | ||
图片预览



文档简介
课件22张PPT。3.3 圆周角和圆心角的关系(1)
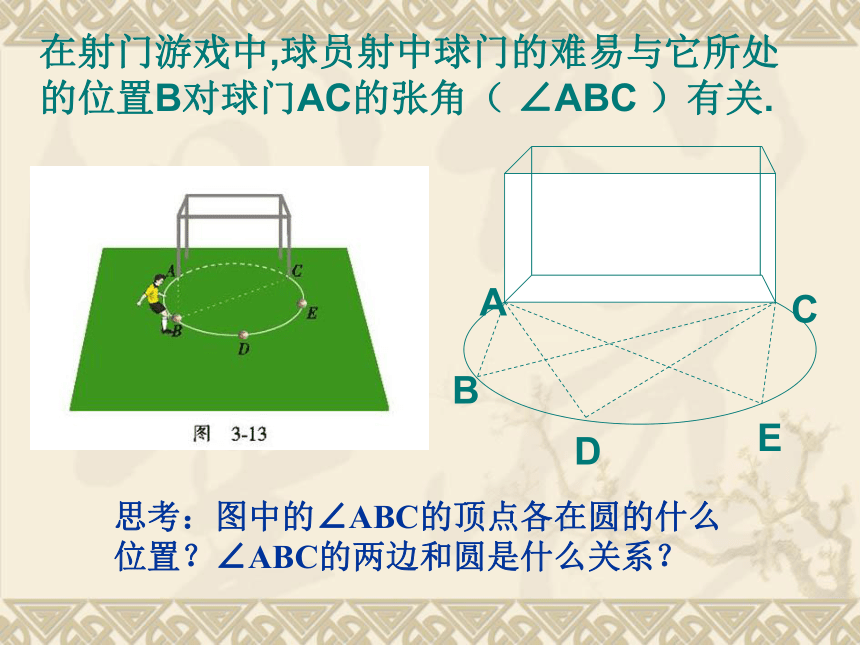
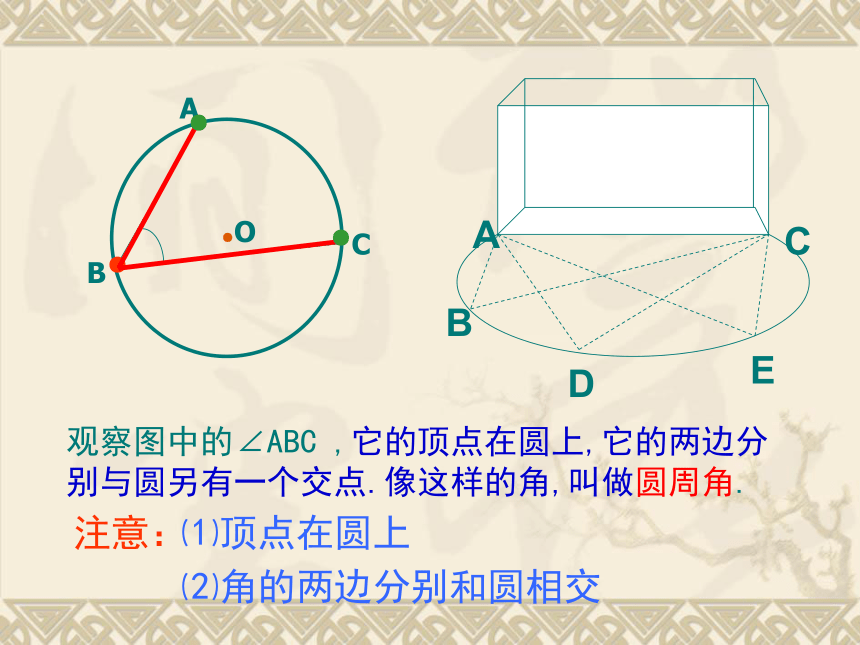
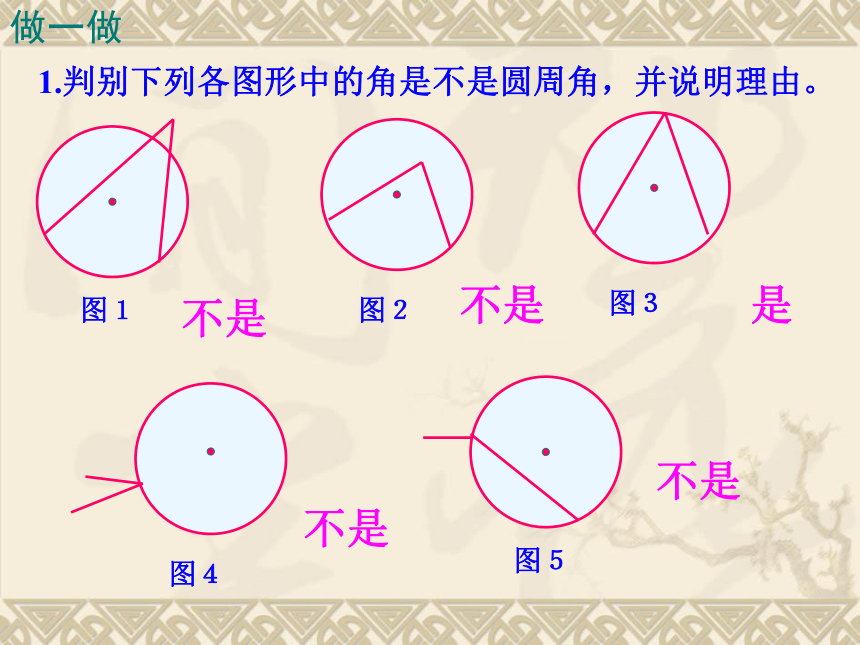
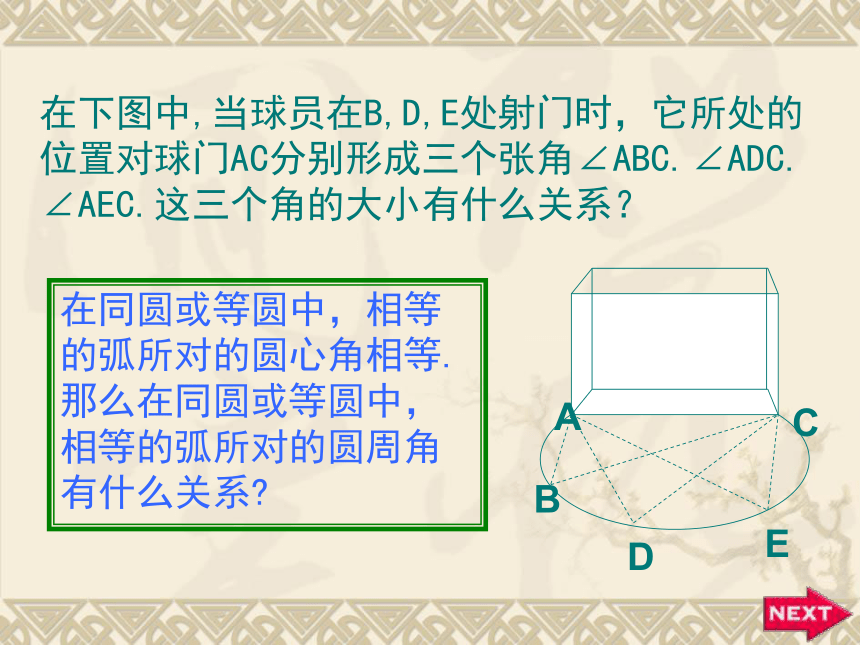
1.圆心角的定义顶点在圆心的角叫圆心角.2.在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。忆一忆若圆心角的顶点位置发生改变,可能出现哪些情形?想一想在射门游戏中,球员射中球门的难易与它所处的位置B对球门AC的张角( ∠ABC )有关.思考:图中的∠ABC的顶点各在圆的什么位置?∠ABC的两边和圆是什么关系?观察图中的∠ABC ,它的顶点在圆上,它的两边分别与圆另有一个交点.像这样的角,叫做圆周角.⑵角的两边分别和圆相交●注意:⑴顶点在圆上●●1.判别下列各图形中的角是不是圆周角,并说明理由。不是不是是不是不是图1图2图3图4图5做一做在下图中,当球员在B,D,E处射门时,它所处的位置对球门AC分别形成三个张角∠ABC.∠ADC. ∠AEC.这三个角的大小有什么关系?在同圆或等圆中,相等的弧所对的圆心角相等.那么在同圆或等圆中,相等的弧所对的圆周角有什么关系?类比圆心角探知圆周角在同圆或等圆中,相等的弧所对的圆心角相等.在同圆或等圆中,相等的弧所对的圆周角有什么关系?我们先来研究一条弧所对的圆周角和圆心角的关系圆周角和圆心角的关系如图,观察圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系?说说你的想法,并与同伴交流.教师提示:注意圆心与圆周角的位置关系.如图,在⊙O中,观察圆周角∠ABC 与圆心角∠AOC ,它们的大小有什么关系?OACB议一议即∠ABC的一边BC过圆心O.∵ ∠AOC 是△ABO的外角, ∴ ∠AOC = ∠ABO+ ∠BAO.∵OA=OB∴ ∠ABO = ∠BAO∴ ∠AOC =2 ∠ABOOACB你能写出这个命题吗?一条弧所对的圆周角等于它所对的圆心角的一半.①.首先考虑一种特殊情况:试一试②当圆心(O)在圆周角(∠ABC)的内部时,圆周角
∠ABC与圆心角∠AOC的大小关系会怎样?
提示:能否转化为①的情况?过点B作直径BD.由①可得:∠ABD = ∠AOD,∠CBD = ∠COD,你能写出这个命题吗?一条弧所对的圆周角等于它所对的圆心角的一半.试一试③当圆心(O)在圆周角(∠ABC)的外部时,圆周
角∠ABC与圆心角∠AOC的大小关系会怎样?
提示:能否也转化为①的情况?
过点B作直径BD.由①可得:
∠ABD = ∠AOD,∠CBD = ∠COD,你能写出这个命题吗?一条弧所对的圆周角等于
它所对的圆心角的一半.试一试圆周角定理同一条弧所对的圆周角等
于它所对的圆心角的一半····100°AO20°O90°ABABBCOBACC(1)(2)(3)(4)AB为直径,求∠ACB求∠AOB求∠AOB求∠A做一做2、如图 .已知圆心角∠AOB的度数为100°.求圆周角∠ACB的度数.AOBC做一做3.如图(1),在⊙O中,∠BAC=50°,求∠C的大小.4.如图(2),在⊙O中,∠B,∠D,∠E的大小有什么关系?为什么?CABDBACDE(1) (2)做一做2.如图.在⊙O中.∠BOC=50°,求∠BAC 的大小.BOCA1.举出生活中含有圆周角的例子.随堂练习习 题 证明:∠ACB= ∠AOB12∠BAC= ∠BOC2∠AOB=2∠BOC∠ACB=2∠BAC1 规律:解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理分析:2再见
1.圆心角的定义顶点在圆心的角叫圆心角.2.在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。忆一忆若圆心角的顶点位置发生改变,可能出现哪些情形?想一想在射门游戏中,球员射中球门的难易与它所处的位置B对球门AC的张角( ∠ABC )有关.思考:图中的∠ABC的顶点各在圆的什么位置?∠ABC的两边和圆是什么关系?观察图中的∠ABC ,它的顶点在圆上,它的两边分别与圆另有一个交点.像这样的角,叫做圆周角.⑵角的两边分别和圆相交●注意:⑴顶点在圆上●●1.判别下列各图形中的角是不是圆周角,并说明理由。不是不是是不是不是图1图2图3图4图5做一做在下图中,当球员在B,D,E处射门时,它所处的位置对球门AC分别形成三个张角∠ABC.∠ADC. ∠AEC.这三个角的大小有什么关系?在同圆或等圆中,相等的弧所对的圆心角相等.那么在同圆或等圆中,相等的弧所对的圆周角有什么关系?类比圆心角探知圆周角在同圆或等圆中,相等的弧所对的圆心角相等.在同圆或等圆中,相等的弧所对的圆周角有什么关系?我们先来研究一条弧所对的圆周角和圆心角的关系圆周角和圆心角的关系如图,观察圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系?说说你的想法,并与同伴交流.教师提示:注意圆心与圆周角的位置关系.如图,在⊙O中,观察圆周角∠ABC 与圆心角∠AOC ,它们的大小有什么关系?OACB议一议即∠ABC的一边BC过圆心O.∵ ∠AOC 是△ABO的外角, ∴ ∠AOC = ∠ABO+ ∠BAO.∵OA=OB∴ ∠ABO = ∠BAO∴ ∠AOC =2 ∠ABOOACB你能写出这个命题吗?一条弧所对的圆周角等于它所对的圆心角的一半.①.首先考虑一种特殊情况:试一试②当圆心(O)在圆周角(∠ABC)的内部时,圆周角
∠ABC与圆心角∠AOC的大小关系会怎样?
提示:能否转化为①的情况?过点B作直径BD.由①可得:∠ABD = ∠AOD,∠CBD = ∠COD,你能写出这个命题吗?一条弧所对的圆周角等于它所对的圆心角的一半.试一试③当圆心(O)在圆周角(∠ABC)的外部时,圆周
角∠ABC与圆心角∠AOC的大小关系会怎样?
提示:能否也转化为①的情况?
过点B作直径BD.由①可得:
∠ABD = ∠AOD,∠CBD = ∠COD,你能写出这个命题吗?一条弧所对的圆周角等于
它所对的圆心角的一半.试一试圆周角定理同一条弧所对的圆周角等
于它所对的圆心角的一半····100°AO20°O90°ABABBCOBACC(1)(2)(3)(4)AB为直径,求∠ACB求∠AOB求∠AOB求∠A做一做2、如图 .已知圆心角∠AOB的度数为100°.求圆周角∠ACB的度数.AOBC做一做3.如图(1),在⊙O中,∠BAC=50°,求∠C的大小.4.如图(2),在⊙O中,∠B,∠D,∠E的大小有什么关系?为什么?CABDBACDE(1) (2)做一做2.如图.在⊙O中.∠BOC=50°,求∠BAC 的大小.BOCA1.举出生活中含有圆周角的例子.随堂练习习 题 证明:∠ACB= ∠AOB12∠BAC= ∠BOC2∠AOB=2∠BOC∠ACB=2∠BAC1 规律:解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理分析:2再见
