图形的相似(浙江省台州市温岭市)
文档属性
| 名称 | 图形的相似(浙江省台州市温岭市) |

|
|
| 格式 | rar | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-01-08 00:00:00 | ||
图片预览







文档简介
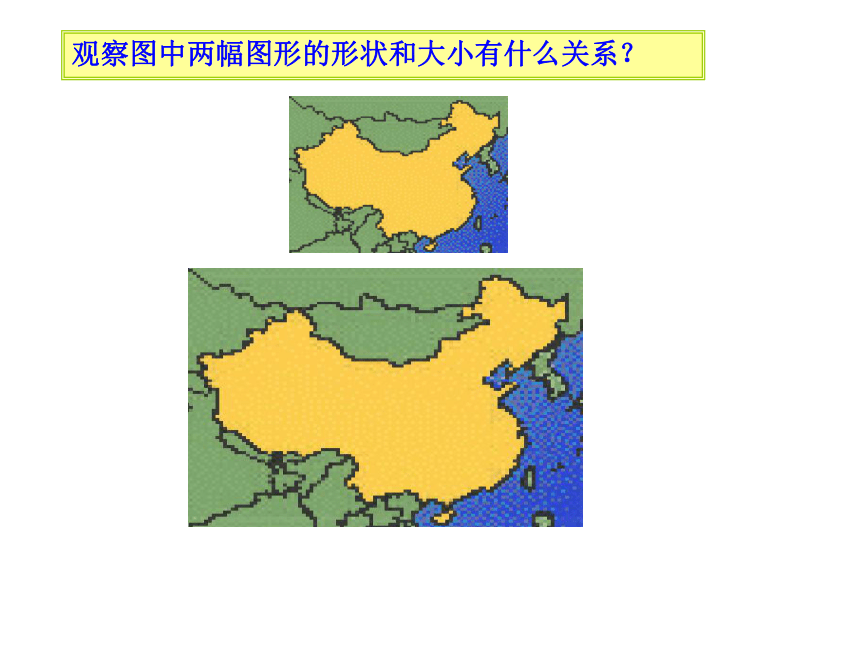
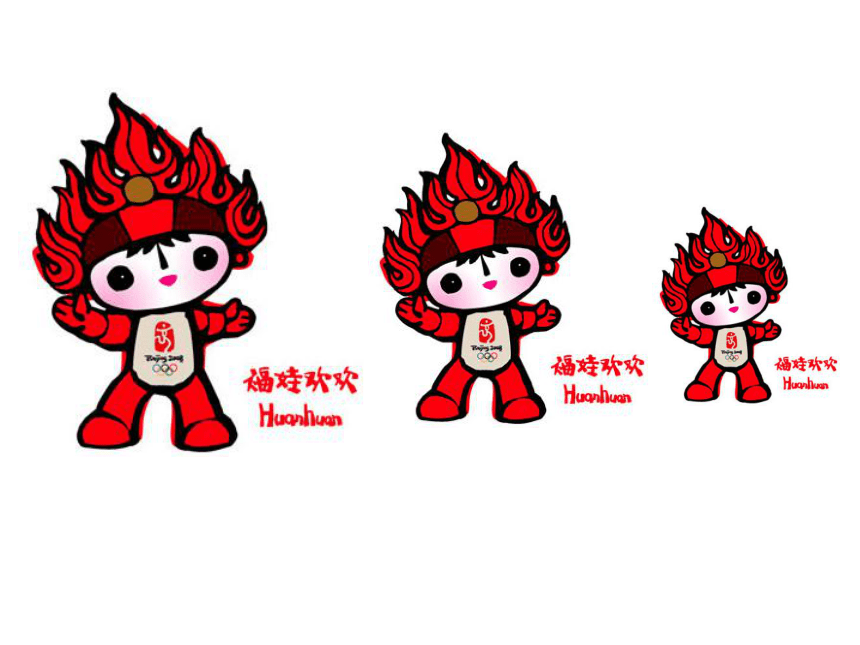
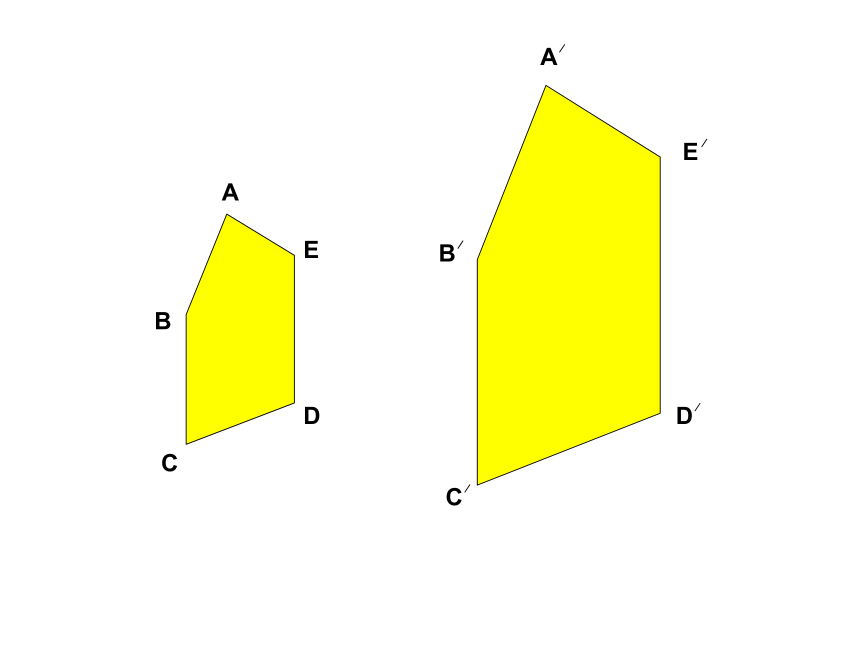
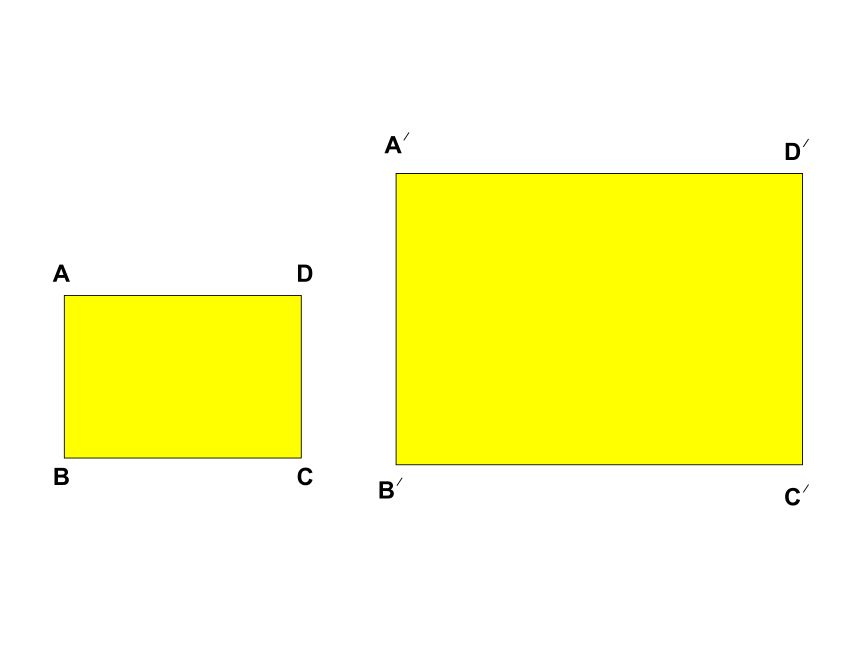
课件50张PPT。相似三角形第一课时观察图中两幅图形的形状和大小有什么关系?试试你的眼力!DCEBA你从上述几组图片发现了什么?它们的大小不一定相等,
形状相同.1.相似形定义:我们把形状相同的两个图形称为相似形。注意:相似图形的大小不一定相同。 你认为下列属性选项中哪个才是相似图形的本质属性? ( )
A、大小不同
B、大小相同
C、形状相同
D、形状不同?C理解概念形状、大小都相同的图形称为全等图形。2、全等图形:注:全等图形是相似图形的特殊情况。3、图形的相似具有传递性; 如果图形A与图形B相似,图形B与图形C相似, 那么图形A与图形C相似。生活中的相似图形理解概念放大镜下的图形和原来的图形相似吗?你看到过哈哈镜吗?哈哈镜中的形象与你本人相似吗?平面镜呢?(A)(B)(C)理解概念1、下列说法正确的是( )
A 、小东上幼儿园时的照片和初中毕业时的照片相似.
B、商店新买来的一副三角板是相似的.
C 、 所有的课本都是相似的.
D 、国旗的五角星都是相似的.
选一选D2、下列哪两个图形是相似图形( )BA、(1)与(2)B、(1)与(3)C、(2)与(3)D、(3)与(4)(1)(2)(3)(4)想一想:观察下面的图形(a)~(g),其中哪些是与图形(1)、(2)或(3)相似的?理解概念解: 1)相似 请把下列各组图形是否相似的结论写在下面的括号里. 试一试2)不相似3)不相似4)相似5)不相似6)不相似(1)(2)(3)(4)(7)(8)你能把下面图形分组吗?(5)(6)对应角……?对应边……?问题1:这两个三角形是否为相似形?相似三角形定义:我们把对应角相等、对应边成比例的两个三角形叫做相似三角形。表示为:
△ABC∽△ A'B'C' 在写两个三角形相似时应把表示对应顶点的字母写在对应的位置上。 注意读作:
△ABC相似于△ A'B'C' △ABC与△ A'B'C'相似用符号语言表示:∴ △ABC∽△A'B'C'(相似三角形的定义可以作为三角形相似的一种判定方法)ab正三角形ABC正三角形A,B,C,问题:正三角形ABC与正三角形A,B,C,相似,它们的对应角、对应边有什么关系?角:∠A=∠ A,∠B=∠ B,∠C=∠ C,边:正方形ABCD正方形A,B,C, D,问题:正方形ABCD与正方形A,B,C, D,相似,它们的对应角、对应边有什么关系?角:∠A=∠ A,∠B=∠ B,∠C=∠ C,边:∠D=∠ D,思考:相似正多边形有怎样的性质呢?1. 下图是两个相似的三角形,它们的对应角有什么关系?对应边的比是否相等?2.对于上图中两个相似的四边形,它们的对应角、对应边是否有同样的结论?1.对应角相等 对应边成比例2. 具有同样的结论多边形相似特征:相似比: 我们把相似多边形对应边的比称为相似比.多边形相似的定义:相似比为1时,相似的两个图形有什么关系?两图形全等ABCDEF2cm3cm那么△ABC与△DEF对应边的比 =已知△ABC∽△DEF,AC=2cm,DF=3cm我们将相似三角形对应边的比称之为相似比。
(用字母k表示)2:3?问题1△ABC与△A'B'C'相似比k1△A'B'C'与△ABC的相似比k2=?=? △ABC∽△A'B'C'问题2三角形的前后次序不同,所得相似比不同。思考1:如果两个多边形角对应相等,那么它们相似吗?为什么?请举例说明。正方形矩形思考2:如果两个多边形对应边的比相等,那么它们相似吗?为什么?请举例说明。正方形菱形两个多边形相似对应角相等对应边的比相等? 归 纳相似多边形的判定:如果两个多边形对应角相等,对应边的比相等,那么这两个多边形相似。例1:如图,四边形ABCD与EFGH相似,求角α、β的大小和EH的长度x解:∵四边形ABCD与EFGH相似∴∠α=∠C=83°∠A=∠E=118°在四边形ABCD中∠β=360°-(78°+83°+118°)=81°又∵∴解得:x=28cm应用新知应用相似多边形的性质解决问题:1、如图,△ABC与△ A,B,C, 相似,
则∠B,= ;
BC= ;
△ABC与△ A,B,C, 相似比为 。应用新知72°404△ A,B,C, 与△ABC相似比为 。 如图所示的每组四边形都相似,则:
⑴如图1,则x= ,y = ,α= ;
⑵如图2,x= .2.5 1.5 90022.5 1、如图,△ABC与△DEF相似,求未知边x,y的长度。ABDF
判断题
(1)两个菱形一定相似 。 ( )
(2)两个菱形,若最大角相等,则一定相似( )
(3)两个矩形一定相似 。 ( )
(4)两个正方形一定相似。 ( )
(5)两个正三角形一定相似。 ( )
(6)有一个角相等的两个平行四边形 ( )
(7)所有正六边形都相似。 ( )√ ××√ √ ×√ (8)所有的直角三角形都相似( ) × 如图所示的两个四边形相似吗?为什么?解:∴两个四边形不相似变式:若EH=60,那么这两个四边形相似吗?60应用新知思维的发散与创新1、已知A4纸的宽度为21cm,如图将其对折后,所得的矩形都和原来的矩形相似,求A4纸的长度。
A421cm对折x0.5x21cm解:∵对折后矩形和原来的矩形相似∴解得:2、现有一长为30cm,宽为15cm的矩形奔马图,在其四周表上宽为2cm的木质边框。那么内外边缘所成的矩形相似吗?30cm15cm34cm19cm思维的发散与创新问题:现有一长为30cm,宽为15cm的矩形奔马图,请动手设计边框,使所得内外边缘所成的矩形相似。动手 设计2
cm1cm1cm2
cm34cm17cm∵∴内外边缘所成的矩形相似。回头一看,我想说…
这节课我收获了什么--------
有哪些东西我上课还没有懂-----
1.相似图形 ——相同形状的图形总结:相似多边形性质2.相似多边形的性质与判定:3.相似比——相似多边形对应边的比谢 谢
形状相同.1.相似形定义:我们把形状相同的两个图形称为相似形。注意:相似图形的大小不一定相同。 你认为下列属性选项中哪个才是相似图形的本质属性? ( )
A、大小不同
B、大小相同
C、形状相同
D、形状不同?C理解概念形状、大小都相同的图形称为全等图形。2、全等图形:注:全等图形是相似图形的特殊情况。3、图形的相似具有传递性; 如果图形A与图形B相似,图形B与图形C相似, 那么图形A与图形C相似。生活中的相似图形理解概念放大镜下的图形和原来的图形相似吗?你看到过哈哈镜吗?哈哈镜中的形象与你本人相似吗?平面镜呢?(A)(B)(C)理解概念1、下列说法正确的是( )
A 、小东上幼儿园时的照片和初中毕业时的照片相似.
B、商店新买来的一副三角板是相似的.
C 、 所有的课本都是相似的.
D 、国旗的五角星都是相似的.
选一选D2、下列哪两个图形是相似图形( )BA、(1)与(2)B、(1)与(3)C、(2)与(3)D、(3)与(4)(1)(2)(3)(4)想一想:观察下面的图形(a)~(g),其中哪些是与图形(1)、(2)或(3)相似的?理解概念解: 1)相似 请把下列各组图形是否相似的结论写在下面的括号里. 试一试2)不相似3)不相似4)相似5)不相似6)不相似(1)(2)(3)(4)(7)(8)你能把下面图形分组吗?(5)(6)对应角……?对应边……?问题1:这两个三角形是否为相似形?相似三角形定义:我们把对应角相等、对应边成比例的两个三角形叫做相似三角形。表示为:
△ABC∽△ A'B'C' 在写两个三角形相似时应把表示对应顶点的字母写在对应的位置上。 注意读作:
△ABC相似于△ A'B'C' △ABC与△ A'B'C'相似用符号语言表示:∴ △ABC∽△A'B'C'(相似三角形的定义可以作为三角形相似的一种判定方法)ab正三角形ABC正三角形A,B,C,问题:正三角形ABC与正三角形A,B,C,相似,它们的对应角、对应边有什么关系?角:∠A=∠ A,∠B=∠ B,∠C=∠ C,边:正方形ABCD正方形A,B,C, D,问题:正方形ABCD与正方形A,B,C, D,相似,它们的对应角、对应边有什么关系?角:∠A=∠ A,∠B=∠ B,∠C=∠ C,边:∠D=∠ D,思考:相似正多边形有怎样的性质呢?1. 下图是两个相似的三角形,它们的对应角有什么关系?对应边的比是否相等?2.对于上图中两个相似的四边形,它们的对应角、对应边是否有同样的结论?1.对应角相等 对应边成比例2. 具有同样的结论多边形相似特征:相似比: 我们把相似多边形对应边的比称为相似比.多边形相似的定义:相似比为1时,相似的两个图形有什么关系?两图形全等ABCDEF2cm3cm那么△ABC与△DEF对应边的比 =已知△ABC∽△DEF,AC=2cm,DF=3cm我们将相似三角形对应边的比称之为相似比。
(用字母k表示)2:3?问题1△ABC与△A'B'C'相似比k1△A'B'C'与△ABC的相似比k2=?=? △ABC∽△A'B'C'问题2三角形的前后次序不同,所得相似比不同。思考1:如果两个多边形角对应相等,那么它们相似吗?为什么?请举例说明。正方形矩形思考2:如果两个多边形对应边的比相等,那么它们相似吗?为什么?请举例说明。正方形菱形两个多边形相似对应角相等对应边的比相等? 归 纳相似多边形的判定:如果两个多边形对应角相等,对应边的比相等,那么这两个多边形相似。例1:如图,四边形ABCD与EFGH相似,求角α、β的大小和EH的长度x解:∵四边形ABCD与EFGH相似∴∠α=∠C=83°∠A=∠E=118°在四边形ABCD中∠β=360°-(78°+83°+118°)=81°又∵∴解得:x=28cm应用新知应用相似多边形的性质解决问题:1、如图,△ABC与△ A,B,C, 相似,
则∠B,= ;
BC= ;
△ABC与△ A,B,C, 相似比为 。应用新知72°404△ A,B,C, 与△ABC相似比为 。 如图所示的每组四边形都相似,则:
⑴如图1,则x= ,y = ,α= ;
⑵如图2,x= .2.5 1.5 90022.5 1、如图,△ABC与△DEF相似,求未知边x,y的长度。ABDF
判断题
(1)两个菱形一定相似 。 ( )
(2)两个菱形,若最大角相等,则一定相似( )
(3)两个矩形一定相似 。 ( )
(4)两个正方形一定相似。 ( )
(5)两个正三角形一定相似。 ( )
(6)有一个角相等的两个平行四边形 ( )
(7)所有正六边形都相似。 ( )√ ××√ √ ×√ (8)所有的直角三角形都相似( ) × 如图所示的两个四边形相似吗?为什么?解:∴两个四边形不相似变式:若EH=60,那么这两个四边形相似吗?60应用新知思维的发散与创新1、已知A4纸的宽度为21cm,如图将其对折后,所得的矩形都和原来的矩形相似,求A4纸的长度。
A421cm对折x0.5x21cm解:∵对折后矩形和原来的矩形相似∴解得:2、现有一长为30cm,宽为15cm的矩形奔马图,在其四周表上宽为2cm的木质边框。那么内外边缘所成的矩形相似吗?30cm15cm34cm19cm思维的发散与创新问题:现有一长为30cm,宽为15cm的矩形奔马图,请动手设计边框,使所得内外边缘所成的矩形相似。动手 设计2
cm1cm1cm2
cm34cm17cm∵∴内外边缘所成的矩形相似。回头一看,我想说…
这节课我收获了什么--------
有哪些东西我上课还没有懂-----
1.相似图形 ——相同形状的图形总结:相似多边形性质2.相似多边形的性质与判定:3.相似比——相似多边形对应边的比谢 谢
