4.2直线、射线、线段第一课时练习(含详细解析)
文档属性
| 名称 | 4.2直线、射线、线段第一课时练习(含详细解析) |  | |
| 格式 | zip | ||
| 文件大小 | 180.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-28 15:10:14 | ||
图片预览



文档简介
新人教版七年级数学上册第四章
§4.2第一课时【直线、射线、线段】课时练习
一.选择题(共10小题)
1.有下列说法:①电线杆可看做射线,②探照灯光线可看做射线,③A地到B地的高速公路可看做一条直线.其中正确的有( )
A. 0个 B.1个 C.2个 D.3个
2.如图,点A、B、C是直线l上的三个点,图中共有线段条数是( )
A.1条 B.2条 C.3条 D.4条
3.如图,点A、B、C在一直线上,则图中共有射线( )
A.1条 B.2条 C.4条 D.6条
4.有三个点A,B,C,过其中每两个点画直线,可以画出直线( )
A.1条 B.2条 C.1条或3条 D.无法确定
5.下列说法中,正确的有( )
①射线与其反向延长线成一条直线;
②直线a,b相交于点m;
③两直线交于两点;
④三条直线两两相交,一定有3个交点.
A.3个 B.2个 C.1个 D.0个
6.延长线段AB到C,下列说法正确的是( )
A.点C在线段AB上 B.点C在直线AB上
C.点C不在直线AB上 D.点C在直线BA的延长线上
7.下列说法中正确的是( )
A.延长射线OA到点B B.线段AB为直线AB的一部分
C.射线OM与射线MO表示同一条射线 D.一条直线由两条射线组成
8.以下说法中正确的语句共有几个( )
①两点确定一条直线;
②延长直线AB到C;
③延长线段AB到C,使得AC=BC;
④反向延长线段BC到D,使BD=BC;
⑤线段AB与线段BA表示同一条线段;
⑥线段AB是直线AB的一部分.
A.3 B.4 C.5 D.6
9.平面内的9条直线任两条都相交,交点数最多有m个,最少有n个,则m+n等于( )
A.36 B.37 C.38 D.39
10.对于直线AB,线段CD,射线EF,在下列各图中能相交的是( )
A. B. C. D.
二.填空题(共3小题)
11.一条直线上有若干个点,以任意两点为端点可以确定一条线段,线段的条数与点的个数之间的对应关系如下表所示.请你探究表内数据间的关系,根据发现的规律,则表中n= .
点的个数
2
3
4
5
6
7
线段的条数
1
3
6
10
15
n
12.平面内画2条直线,有 个交点,3条直线最多有 个交点,4条直线最多有 个交点,5条直线最多有 个交点,n条直线最多有 个交点.
13.如图:火车从A地到B地途经C,D,E,F四个车站,且相邻两站之间的距离各不相同,
则售票员应准备 种票价的车票.
三.解答题(共7小题)
14.请你先动笔在草稿纸上画一画,再回答下列问题:
(1)平面内两条直线,可以把平面分成几部分?
(2)平面内3条直线,可以把平面分成几部分?
(3)平面内4条直线,可以把平面最多分成多少部分?
(4)平面内100条直线,可以把平面最多分成多少部分?
15.指出下列句子的错误,并加以改正:
(1)如图1,在线段AB的延长线上取一点C;
(2)如图2,延长直线AB,使它与直线CD相交于点P;
(3)如图3,延长射线OA,使它和线段BC相交于点D.
16.用适当语句表述图中点与直线的关系:
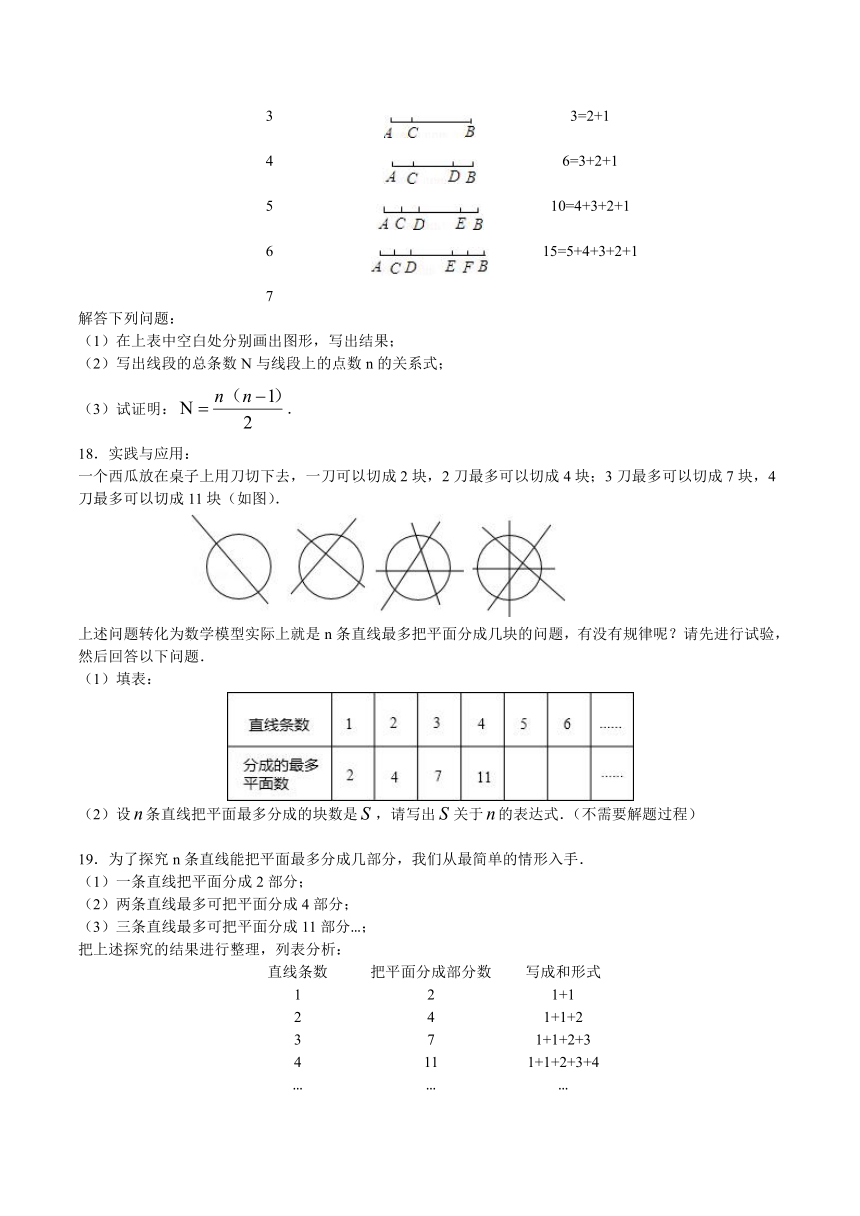
17.阅读下表:
线段AB上的点数n(包括A、B两点)
图例
线段总条数N
3
3=2+1
4
6=3+2+1
5
10=4+3+2+1
6
15=5+4+3+2+1
7
解答下列问题:
(1)在上表中空白处分别画出图形,写出结果;
(2)写出线段的总条数N与线段上的点数n的关系式;
(3)试证明:.
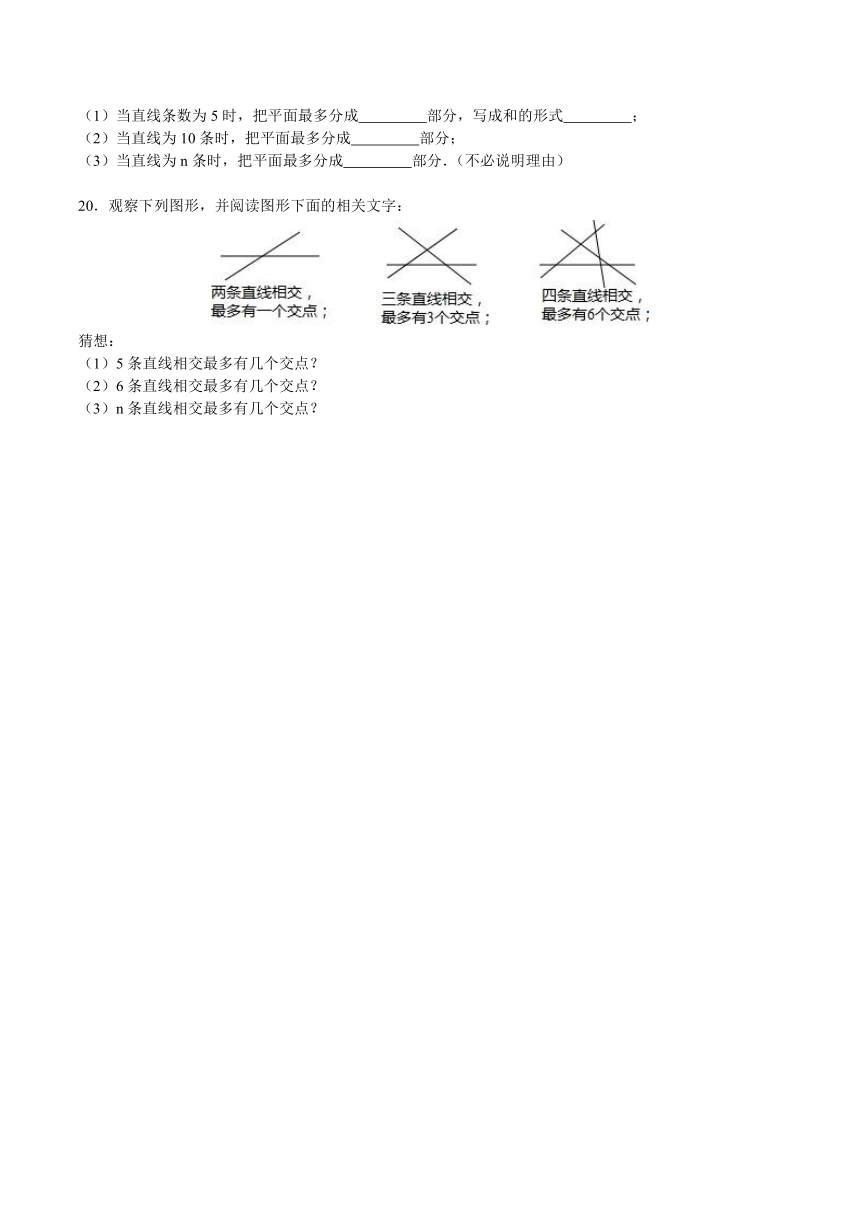
18.实践与应用:
一个西瓜放在桌子上用刀切下去,一刀可以切成2块,2刀最多可以切成4块;3刀最多可以切成7块,4刀最多可以切成11块(如图).
上述问题转化为数学模型实际上就是n条直线最多把平面分成几块的问题,有没有规律呢?请先进行试验,然后回答以下问题.
(1)填表:
(2)设条直线把平面最多分成的块数是,请写出关于的表达式.(不需要解题过程)
19.为了探究n条直线能把平面最多分成几部分,我们从最简单的情形入手.
(1)一条直线把平面分成2部分;
(2)两条直线最多可把平面分成4部分;
(3)三条直线最多可把平面分成11部分…;
把上述探究的结果进行整理,列表分析:
直线条数
把平面分成部分数
写成和形式
1
2
1+1
2
4
1+1+2
3
7
1+1+2+3
4
11
1+1+2+3+4
…
…
…
(1)当直线条数为5时,把平面最多分成 部分,写成和的形式 ;
(2)当直线为10条时,把平面最多分成 部分;
(3)当直线为n条时,把平面最多分成 部分.(不必说明理由)
20.观察下列图形,并阅读图形下面的相关文字:
猜想:
(1)5条直线相交最多有几个交点?
(2)6条直线相交最多有几个交点?
(3)n条直线相交最多有几个交点?
新人教版七年级数学上册第四章
【直线、射线、线段】课时练习
参考答案与试题解析
一.选择题(共10小题)
1.有下列说法:①电线杆可看做射线,②探照灯光线可看做射线,③A地到B地的高速公路可看做一条直线.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
考点:直线、射线、线段.
分析:根据射线、直线及线段的特点进行判断即可.
解答:解:①电线杆只能看作线段,故本项错误;
②探照灯光线可看做射线,说法正确,故本项正确;
③A地到B地的高速公路可看做一条线段,故本项错误;
综上可得正确的有1个.
故选B.
点评:本题考查了直线、射线、线段的知识,属于基础题,解答本题的关键是掌握三者的特点.
2.如图,点A、B、C是直线l上的三个点,图中共有线段条数是( )
A.1条 B.2条 C.3条 D.4条
考点:直线、射线、线段.
分析:写出所有的线段,然后再计算条数.
解答:解:图中线段有:线段AB、线段AC、线段BC,共三条.故选C.
点评:记住线段是直线上两点及其之间的部分是解题的关键.
3.如图,点A、B、C在一直线上,则图中共有射线( )
A.1条 B.2条 C.4条 D.6条
考点:直线、射线、线段.
分析:根据射线的定义,一条直线上的每个点可以有两条射线,分析图形可得答案.
解答:解:根据射线的定义,这条直线上的每个点可以有两条射线,
故图中共有射线6条.
故选D.
点评:本题考查射线的定义.
4.有三个点A,B,C,过其中每两个点画直线,可以画出直线( )
A.1条 B.2条 C.1条或3条 D.无法确定
考点:直线、射线、线段.
分析:此题考查直线的基本性质:两点确定一条直线.
解答:解:∵三点在一条直线上能画一条直线,三点不在一条直线上能画三条直线;故选C.
点评:注意对题目中已知条件的不同情况的分析.
5.下列说法中,正确的有( )
①射线与其反向延长线成一条直线;
②直线a,b相交于点m;
③两直线交于两点;
④三条直线两两相交,一定有3个交点.
A.3个 B.2个 C.1个 D.0个
考点:直线、射线、线段.
分析:根据直线、射线和线段的定义以及点的表示对各小题分析判断即可得解.
解答:解:①射线与其反向延长线成一条直线,正确;
②直线a,b相交于点m,错误,点应该用大写字母表示;
③两直线交于两点,错误;
④三条直线两两相交,一定有3个交点,错误,三条直线可以经过同一个点.
综上所述,正确的有1个.
故选C.
点评:本题考查了直线、射线和线段,是基础题,熟记相关概念是解题的关键.
6.延长线段AB到C,下列说法正确的是( )
A.点C在线段AB上 B.点C在直线AB上
C.点C不在直线AB上 D.点C在直线BA的延长线上
考点:直线、射线、线段.
分析:本题根据直线、线段、以及射线的概念来解答即可.
解答:解:因为线段有两个端点,所以线段可以向两方延长,
所以点C不在线段AB上,点C在直线AB上,故A、C错误,B正确,
因为直线没有端点,可以向两方无限延伸,直线没有延长线的说法,故D错误.
故选B.
点评:本题考查了直线、射线、线段,熟记概念是解题的关键.
7.下列说法中正确的是( )
A.延长射线OA到点B B.线段AB为直线AB的一部分
C.射线OM与射线MO表示同一条射线 D.一条直线由两条射线组成
考点:直线、射线、线段.
分析:利用直线、射线、线段的特征判定即可.
解答:解:A、延长射线OA到点B,射线OA是无限延伸的,故选项错误;
B、线段AB为直线AB的一部分是正确的;
C、射线OM与射线MO表示两条射线,故选项错误;
D、一条直线不一定由两条射线组成,故选项错误.
故选:B.
点评:本题主要考查了直线、射线、线段,解题的关键是明确直线、射线、线段的特征.
8.以下说法中正确的语句共有几个( )
①两点确定一条直线;
②延长直线AB到C;
③延长线段AB到C,使得AC=BC;
④反向延长线段BC到D,使BD=BC;
⑤线段AB与线段BA表示同一条线段;
⑥线段AB是直线AB的一部分.
A.3 B.4 C.5 D.6
考点:直线、射线、线段.
分析:直线本身是向两方无限延长的,射线是向一方无限延长的,线段有两个端点,不是向两方无限延长的.
解答:解:①两点确定一条直线是正确的;
②直线本身是向两方无限延长的,故说法错误;
③延长线段AB到C,AC>BC,故说法错误;
④反向延长线段BC到D,使BD=BC是正确的;
⑤线段AB与线段BA表示同一条线段是正确的;
⑥线段AB是直线AB的一部分是正确的.
故正确的语句共有4个.
故选:B.
点评:此题主要考查了直线、射线、线段,关键是掌握三种线的性质.
9.平面内的9条直线任两条都相交,交点数最多有m个,最少有n个,则m+n等于( )
A.36 B.37 C.38 D.39
考点:直线、射线、线段.
专题:压轴题;规律型.
分析:求出平面内的9条直线任两条都相交,交点数最多的个数,再求得最少的个数;则即可求得m+n的值.
解答:解:三条最多交点数的情况.就是第三条与前面两条都相交:1+2
四条最多交点数的情况.就是第四条与前面三条都相交:1+2+3
五条最多交点数的情况.就是第五条与前面四条都相交:1+2+3+4
六条最多交点数的情况.就是第六条与前面五条都相交:1+2+3+4+5
七条最多交点数的情况.就是第七条与前面六条都相交:1+2+3+5+6
八条最多交点数的情况.就是第八条与前面七条都相交:1+2+3+5+6+7
九条最多交点数的情况.就是第九条与前面八条都相交:1+2+3+4+5+6+7+8=36
则m+n=1+36=37
故答案B.
点评:此题考查了平面图形,主要培养学生的观察能力和几何想象能力.
10.对于直线AB,线段CD,射线EF,在下列各图中能相交的是( )
A. B. C. D.
考点:直线、射线、线段.
分析:根据直线能向两方无限延伸,射线能向一方无限延伸,线段不能延伸,据此进行选择.
解答:解:B中这条直线与这条射线能相交;A、C、D中直线和射线不能相交.故选B.
点评:本题考查了直线、射线和线段的性质.
二.填空题(共3小题)
11.一条直线上有若干个点,以任意两点为端点可以确定一条线段,线段的条数与点的个数之间的对应关系如下表所示.请你探究表内数据间的关系,根据发现的规律,则表中n= 21 .
点的个数
2
3
4
5
6
7
线段的条数
1
3
6
10
15
n
考点:直线、射线、线段.
专题:压轴题;规律型.
分析:根据表中数据,寻找规律,列出公式解答.
解答:解:设线段有n个点,分成的线段有m条.有以下规律:
n个 m条
2 1
3 1+2
4 1+2+3
…
n m=1+…+(n﹣1)=
7个点把线段AB共分成=21条.
点评:本题体现了“具体﹣﹣﹣抽象﹣﹣﹣﹣具体”的思维探索过程,探索规律、运用规律,有利于培养学生健全的思维能力.
12.平面内画2条直线,有 0或1 个交点,3条直线最多有 3 个交点,4条直线最多有 6 个交点,5条直线最多有 10 个交点,n条直线最多有 个交点.
考点:直线、射线、线段.
分析:直接得出2、3、4、5条直线相交的最多交点的个数;根据交点的个数的计算方法列式计算即可得解.
解答:解:平面内画2条直线,有 0或1个交点,
3条直线最多有1+2=3交点,
4条直线最多有1+2+3=6个交点,
5条直线最多有1+2+3+4=10个交点,
n条直线最多有1+2+3+…+(n﹣1)=个交点.
故答案为:0或1;3;6;10;.
点评:本题考查了直线、射线、线段,主要是相交直线交点个数的规律探索,熟记计算方法是解题的关键.
13.如图:火车从A地到B地途经C,D,E,F四个车站,且相邻两站之间的距离各不相同,则售票员应准备 15 种票价的车票.
考点:直线、射线、线段.
分析:先找出所有线段的条数,再根据车票有顺序,求解即可.
解答:解:由图可知图上的线段为:AC、AD、AE、AF、AB、CD、CE、CF、CB、DE、DF、DB、EF、EB、FB共15条,所以共需要15种.
点评:本题的实质是求线段的数量,体现了数形结合的思想.
三.解答题(共7小题)
14.请你先动笔在草稿纸上画一画,再回答下列问题:
(1)平面内两条直线,可以把平面分成几部分?
(2)平面内3条直线,可以把平面分成几部分?
(3)平面内4条直线,可以把平面最多分成多少部分?
(4)平面内100条直线,可以把平面最多分成多少部分?
考点:直线、射线、线段.
专题:规律型.
分析:(1)(2)(3)这根据题意画图即可;
(4)根据(1)(2)(3)的数值得出规律,再根据规律解题.
解答:解:(1)如下图:可分成3个或4个平面;
(2)如下图:可分成4,6,7个平面;
(3)如下图:最可多分成11个.
(4)如图:一条直线可以把平面分成两部分,两条直线最多可以把平面分成4部分,三条直线最多可以把平面分成7部分,四条直线最多可以把平面分成11部分,可以发现,两条直线时多了2部分,三条直线比原来多了3部分,四条直线时比原来多了4部分,…,n条时比原来多了n部分.
因为n=1,a1=1+1,
n=2,a2=a1+2,
n=3,a3=a2+3,
n=4,a4=a3+4,
…
n=n,an=an﹣1+n,
以上式子相加整理得,an=1+1+2+3+…+n=1+.
100个时可分成1+=1+5050=5051.
点评:本题考查了直线射线和线段,要知道从一般到具体的探究方法,并找到规律.
15.指出下列句子的错误,并加以改正:
(1)如图1,在线段AB的延长线上取一点C;
(2)如图2,延长直线AB,使它与直线CD相交于点P;
(3)如图3,延长射线OA,使它和线段BC相交于点D.
考点:直线、射线、线段.
分析:(1)利用延长线的方向确定字母循序;
(2)直线无法延长,直接利用直线相交得出即可;
(3)应反向延长射线OA,得出即可.
解答:解:(1)如图1,应为:在线段BA的延长线上取一点C;
(2)如图2,应为:直线AB与直线CD相交于点P;
(3)如图3,反向延长射线OA,使它和线段BC相交于点D.
点评:此题主要考查了直线、射线、线段的定义,正确把握相关定义是解题关键.
16.用适当语句表述图中点与直线的关系:
考点:直线、射线、线段.
分析:(1)根据直线的位置关系以及点与直线的位置关系即可解答;
(2)直线a、b、c两两相交,再说明交点即可
解答:解:图1,直线l经过点A、B,点P在直线l外;
图2,直线a、b、c两两相交,直线a与直线c交于点C,直线a与直线b交于点B,直线b与直线c交于点A.
点评:本题主要考查了几何作图,注意叙述要准确.
17.阅读下表:
线段AB上的点数n(包括A、B两点)
图例
线段总条数N
3
3=2+1
4
6=3+2+1
5
10=4+3+2+1
6
15=5+4+3+2+1
7
解答下列问题:
(1)在上表中空白处分别画出图形,写出结果;
(2)写出线段的总条数N与线段上的点数n的关系式;
(3)试证明:N= .
考点:直线、射线、线段.
专题:规律型.
分析:(1)根据图中规律画出图形,写出结果;
(2)线段的总条数N与线段上的点数n的关系式N= ;
(3)由(1)的规律证明.
解答:解:(1)如图;
(2)N= ;
证明:(3)线段上有3个点时,线段总条数是3条,则3=1+2,
线段上有4个点时,线段总条数是6条,则6=3+2+1,
线段上有5个点时,线段总条数是10条,则10=4+3+2+1,
故线段上有n个点时,线段总条数(n﹣1)+…+3+2+1,则N= .
点评:此题在线段的基础上,着重培养学生的观察、实验和猜想、归纳能力,掌握从特殊向一般猜想的方法.
18.实践与应用:
一个西瓜放在桌子上用刀切下去,一刀可以切成2块,2刀最多可以切成4块;3刀最多可以切成7块,4刀最多可以切成11块(如图).
上述问题转化为数学模型实际上就是n条直线最多把平面分成几块的问题,有没有规律呢?请先进行试验,然后回答以下问题.
(1)填表:
(2)设n条直线把平面最多分成的块数是S,请写出S关于n的表达式.(不需要解题过程)
考点:直线、射线、线段.
专题:规律型.
分析:可以发现,两条直线时比原来多了2块,三条直线比原来多了3块,四条直线时比原来多了4块,…,n条时比原来多了n块,
∴n=1,S1=1+1
n=2,S2=S1+2
n=3,S3=S2+3
n=4,S4=S3+4
…
n=n,Sn=Sn﹣1+n
以上式子相加整理得,Sn=1+1+2+3+…+n=1+.
解答:解:(1)n=5,S5=1+1+2+3+4+5=16,
n=6,S6=1+1+2+3+4+5+6=22;
(2)Sn=1+1+2+3+…+n=1+.
点评:本题是找规律题,解题的关键是找到Sn=1+1+2+3+…+n=1+.
19.为了探究n条直线能把平面最多分成几部分,我们从最简单的情形入手.
(1)一条直线把平面分成2部分;
(2)两条直线最多可把平面分成4部分;
(3)三条直线最多可把平面分成11部分…;
把上述探究的结果进行整理,列表分析:
直线条数
把平面分成部分数
写成和形式
1
2
1+1
2
4
1+1+2
3
7
1+1+2+3
4
11
1+1+2+3+4
…
…
…
(1)当直线条数为5时,把平面最多分成 16 部分,写成和的形式 1+1+2+3+4+5 ;
(2)当直线为10条时,把平面最多分成 56 部分;
(3)当直线为n条时,把平面最多分成 +1 部分.(不必说明理由)
考点:直线、射线、线段.
专题:图表型.
分析:根据表中数据,总结出规律,再根据规律解题.
解答:解:(1)根据表中规律,当直线条数为5时,把平面最多分成16部分,1+1+2+3+4+5=16;
(2)根据表中规律,当直线为10条时,把平面最多分成56部分,为1+1+2+3+…+10=56;
(3)设直线条数有n条,分成的平面最多有m个.
有以下规律:
n m
1 1+1
2 1+1+2
3 1+1+2+3
:
:
:
n m=1+1+2+3+…+n=+1.
点评:本题体现了由“特殊到一般再到特殊”的思维过程,有利于培养同学们的探究意识.
20.观察下列图形,并阅读图形下面的相关文字:
猜想:
(1)5条直线相交最多有几个交点?
(2)6条直线相交最多有几个交点?
(3)n条直线相交最多有几个交点?
考点:直线、射线、线段.
专题:规律型.
分析:先观察图形,找出交点的个数与直线的条数之间的关系,然后进行计算即可.
解答:解:解:①5条直线相交最多有=10个交点;
②6条直线相交最多有=15个交点;
③n条直线相交最多有个交点.
点评:此题考查了相交线,关键是观察图形,找出规律,用到的知识点是同一平面内内n条直线相交最多有个交点.
§4.2第一课时【直线、射线、线段】课时练习
一.选择题(共10小题)
1.有下列说法:①电线杆可看做射线,②探照灯光线可看做射线,③A地到B地的高速公路可看做一条直线.其中正确的有( )
A. 0个 B.1个 C.2个 D.3个
2.如图,点A、B、C是直线l上的三个点,图中共有线段条数是( )
A.1条 B.2条 C.3条 D.4条
3.如图,点A、B、C在一直线上,则图中共有射线( )
A.1条 B.2条 C.4条 D.6条
4.有三个点A,B,C,过其中每两个点画直线,可以画出直线( )
A.1条 B.2条 C.1条或3条 D.无法确定
5.下列说法中,正确的有( )
①射线与其反向延长线成一条直线;
②直线a,b相交于点m;
③两直线交于两点;
④三条直线两两相交,一定有3个交点.
A.3个 B.2个 C.1个 D.0个
6.延长线段AB到C,下列说法正确的是( )
A.点C在线段AB上 B.点C在直线AB上
C.点C不在直线AB上 D.点C在直线BA的延长线上
7.下列说法中正确的是( )
A.延长射线OA到点B B.线段AB为直线AB的一部分
C.射线OM与射线MO表示同一条射线 D.一条直线由两条射线组成
8.以下说法中正确的语句共有几个( )
①两点确定一条直线;
②延长直线AB到C;
③延长线段AB到C,使得AC=BC;
④反向延长线段BC到D,使BD=BC;
⑤线段AB与线段BA表示同一条线段;
⑥线段AB是直线AB的一部分.
A.3 B.4 C.5 D.6
9.平面内的9条直线任两条都相交,交点数最多有m个,最少有n个,则m+n等于( )
A.36 B.37 C.38 D.39
10.对于直线AB,线段CD,射线EF,在下列各图中能相交的是( )
A. B. C. D.
二.填空题(共3小题)
11.一条直线上有若干个点,以任意两点为端点可以确定一条线段,线段的条数与点的个数之间的对应关系如下表所示.请你探究表内数据间的关系,根据发现的规律,则表中n= .
点的个数
2
3
4
5
6
7
线段的条数
1
3
6
10
15
n
12.平面内画2条直线,有 个交点,3条直线最多有 个交点,4条直线最多有 个交点,5条直线最多有 个交点,n条直线最多有 个交点.
13.如图:火车从A地到B地途经C,D,E,F四个车站,且相邻两站之间的距离各不相同,
则售票员应准备 种票价的车票.
三.解答题(共7小题)
14.请你先动笔在草稿纸上画一画,再回答下列问题:
(1)平面内两条直线,可以把平面分成几部分?
(2)平面内3条直线,可以把平面分成几部分?
(3)平面内4条直线,可以把平面最多分成多少部分?
(4)平面内100条直线,可以把平面最多分成多少部分?
15.指出下列句子的错误,并加以改正:
(1)如图1,在线段AB的延长线上取一点C;
(2)如图2,延长直线AB,使它与直线CD相交于点P;
(3)如图3,延长射线OA,使它和线段BC相交于点D.
16.用适当语句表述图中点与直线的关系:
17.阅读下表:
线段AB上的点数n(包括A、B两点)
图例
线段总条数N
3
3=2+1
4
6=3+2+1
5
10=4+3+2+1
6
15=5+4+3+2+1
7
解答下列问题:
(1)在上表中空白处分别画出图形,写出结果;
(2)写出线段的总条数N与线段上的点数n的关系式;
(3)试证明:.
18.实践与应用:
一个西瓜放在桌子上用刀切下去,一刀可以切成2块,2刀最多可以切成4块;3刀最多可以切成7块,4刀最多可以切成11块(如图).
上述问题转化为数学模型实际上就是n条直线最多把平面分成几块的问题,有没有规律呢?请先进行试验,然后回答以下问题.
(1)填表:
(2)设条直线把平面最多分成的块数是,请写出关于的表达式.(不需要解题过程)
19.为了探究n条直线能把平面最多分成几部分,我们从最简单的情形入手.
(1)一条直线把平面分成2部分;
(2)两条直线最多可把平面分成4部分;
(3)三条直线最多可把平面分成11部分…;
把上述探究的结果进行整理,列表分析:
直线条数
把平面分成部分数
写成和形式
1
2
1+1
2
4
1+1+2
3
7
1+1+2+3
4
11
1+1+2+3+4
…
…
…
(1)当直线条数为5时,把平面最多分成 部分,写成和的形式 ;
(2)当直线为10条时,把平面最多分成 部分;
(3)当直线为n条时,把平面最多分成 部分.(不必说明理由)
20.观察下列图形,并阅读图形下面的相关文字:
猜想:
(1)5条直线相交最多有几个交点?
(2)6条直线相交最多有几个交点?
(3)n条直线相交最多有几个交点?
新人教版七年级数学上册第四章
【直线、射线、线段】课时练习
参考答案与试题解析
一.选择题(共10小题)
1.有下列说法:①电线杆可看做射线,②探照灯光线可看做射线,③A地到B地的高速公路可看做一条直线.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
考点:直线、射线、线段.
分析:根据射线、直线及线段的特点进行判断即可.
解答:解:①电线杆只能看作线段,故本项错误;
②探照灯光线可看做射线,说法正确,故本项正确;
③A地到B地的高速公路可看做一条线段,故本项错误;
综上可得正确的有1个.
故选B.
点评:本题考查了直线、射线、线段的知识,属于基础题,解答本题的关键是掌握三者的特点.
2.如图,点A、B、C是直线l上的三个点,图中共有线段条数是( )
A.1条 B.2条 C.3条 D.4条
考点:直线、射线、线段.
分析:写出所有的线段,然后再计算条数.
解答:解:图中线段有:线段AB、线段AC、线段BC,共三条.故选C.
点评:记住线段是直线上两点及其之间的部分是解题的关键.
3.如图,点A、B、C在一直线上,则图中共有射线( )
A.1条 B.2条 C.4条 D.6条
考点:直线、射线、线段.
分析:根据射线的定义,一条直线上的每个点可以有两条射线,分析图形可得答案.
解答:解:根据射线的定义,这条直线上的每个点可以有两条射线,
故图中共有射线6条.
故选D.
点评:本题考查射线的定义.
4.有三个点A,B,C,过其中每两个点画直线,可以画出直线( )
A.1条 B.2条 C.1条或3条 D.无法确定
考点:直线、射线、线段.
分析:此题考查直线的基本性质:两点确定一条直线.
解答:解:∵三点在一条直线上能画一条直线,三点不在一条直线上能画三条直线;故选C.
点评:注意对题目中已知条件的不同情况的分析.
5.下列说法中,正确的有( )
①射线与其反向延长线成一条直线;
②直线a,b相交于点m;
③两直线交于两点;
④三条直线两两相交,一定有3个交点.
A.3个 B.2个 C.1个 D.0个
考点:直线、射线、线段.
分析:根据直线、射线和线段的定义以及点的表示对各小题分析判断即可得解.
解答:解:①射线与其反向延长线成一条直线,正确;
②直线a,b相交于点m,错误,点应该用大写字母表示;
③两直线交于两点,错误;
④三条直线两两相交,一定有3个交点,错误,三条直线可以经过同一个点.
综上所述,正确的有1个.
故选C.
点评:本题考查了直线、射线和线段,是基础题,熟记相关概念是解题的关键.
6.延长线段AB到C,下列说法正确的是( )
A.点C在线段AB上 B.点C在直线AB上
C.点C不在直线AB上 D.点C在直线BA的延长线上
考点:直线、射线、线段.
分析:本题根据直线、线段、以及射线的概念来解答即可.
解答:解:因为线段有两个端点,所以线段可以向两方延长,
所以点C不在线段AB上,点C在直线AB上,故A、C错误,B正确,
因为直线没有端点,可以向两方无限延伸,直线没有延长线的说法,故D错误.
故选B.
点评:本题考查了直线、射线、线段,熟记概念是解题的关键.
7.下列说法中正确的是( )
A.延长射线OA到点B B.线段AB为直线AB的一部分
C.射线OM与射线MO表示同一条射线 D.一条直线由两条射线组成
考点:直线、射线、线段.
分析:利用直线、射线、线段的特征判定即可.
解答:解:A、延长射线OA到点B,射线OA是无限延伸的,故选项错误;
B、线段AB为直线AB的一部分是正确的;
C、射线OM与射线MO表示两条射线,故选项错误;
D、一条直线不一定由两条射线组成,故选项错误.
故选:B.
点评:本题主要考查了直线、射线、线段,解题的关键是明确直线、射线、线段的特征.
8.以下说法中正确的语句共有几个( )
①两点确定一条直线;
②延长直线AB到C;
③延长线段AB到C,使得AC=BC;
④反向延长线段BC到D,使BD=BC;
⑤线段AB与线段BA表示同一条线段;
⑥线段AB是直线AB的一部分.
A.3 B.4 C.5 D.6
考点:直线、射线、线段.
分析:直线本身是向两方无限延长的,射线是向一方无限延长的,线段有两个端点,不是向两方无限延长的.
解答:解:①两点确定一条直线是正确的;
②直线本身是向两方无限延长的,故说法错误;
③延长线段AB到C,AC>BC,故说法错误;
④反向延长线段BC到D,使BD=BC是正确的;
⑤线段AB与线段BA表示同一条线段是正确的;
⑥线段AB是直线AB的一部分是正确的.
故正确的语句共有4个.
故选:B.
点评:此题主要考查了直线、射线、线段,关键是掌握三种线的性质.
9.平面内的9条直线任两条都相交,交点数最多有m个,最少有n个,则m+n等于( )
A.36 B.37 C.38 D.39
考点:直线、射线、线段.
专题:压轴题;规律型.
分析:求出平面内的9条直线任两条都相交,交点数最多的个数,再求得最少的个数;则即可求得m+n的值.
解答:解:三条最多交点数的情况.就是第三条与前面两条都相交:1+2
四条最多交点数的情况.就是第四条与前面三条都相交:1+2+3
五条最多交点数的情况.就是第五条与前面四条都相交:1+2+3+4
六条最多交点数的情况.就是第六条与前面五条都相交:1+2+3+4+5
七条最多交点数的情况.就是第七条与前面六条都相交:1+2+3+5+6
八条最多交点数的情况.就是第八条与前面七条都相交:1+2+3+5+6+7
九条最多交点数的情况.就是第九条与前面八条都相交:1+2+3+4+5+6+7+8=36
则m+n=1+36=37
故答案B.
点评:此题考查了平面图形,主要培养学生的观察能力和几何想象能力.
10.对于直线AB,线段CD,射线EF,在下列各图中能相交的是( )
A. B. C. D.
考点:直线、射线、线段.
分析:根据直线能向两方无限延伸,射线能向一方无限延伸,线段不能延伸,据此进行选择.
解答:解:B中这条直线与这条射线能相交;A、C、D中直线和射线不能相交.故选B.
点评:本题考查了直线、射线和线段的性质.
二.填空题(共3小题)
11.一条直线上有若干个点,以任意两点为端点可以确定一条线段,线段的条数与点的个数之间的对应关系如下表所示.请你探究表内数据间的关系,根据发现的规律,则表中n= 21 .
点的个数
2
3
4
5
6
7
线段的条数
1
3
6
10
15
n
考点:直线、射线、线段.
专题:压轴题;规律型.
分析:根据表中数据,寻找规律,列出公式解答.
解答:解:设线段有n个点,分成的线段有m条.有以下规律:
n个 m条
2 1
3 1+2
4 1+2+3
…
n m=1+…+(n﹣1)=
7个点把线段AB共分成=21条.
点评:本题体现了“具体﹣﹣﹣抽象﹣﹣﹣﹣具体”的思维探索过程,探索规律、运用规律,有利于培养学生健全的思维能力.
12.平面内画2条直线,有 0或1 个交点,3条直线最多有 3 个交点,4条直线最多有 6 个交点,5条直线最多有 10 个交点,n条直线最多有 个交点.
考点:直线、射线、线段.
分析:直接得出2、3、4、5条直线相交的最多交点的个数;根据交点的个数的计算方法列式计算即可得解.
解答:解:平面内画2条直线,有 0或1个交点,
3条直线最多有1+2=3交点,
4条直线最多有1+2+3=6个交点,
5条直线最多有1+2+3+4=10个交点,
n条直线最多有1+2+3+…+(n﹣1)=个交点.
故答案为:0或1;3;6;10;.
点评:本题考查了直线、射线、线段,主要是相交直线交点个数的规律探索,熟记计算方法是解题的关键.
13.如图:火车从A地到B地途经C,D,E,F四个车站,且相邻两站之间的距离各不相同,则售票员应准备 15 种票价的车票.
考点:直线、射线、线段.
分析:先找出所有线段的条数,再根据车票有顺序,求解即可.
解答:解:由图可知图上的线段为:AC、AD、AE、AF、AB、CD、CE、CF、CB、DE、DF、DB、EF、EB、FB共15条,所以共需要15种.
点评:本题的实质是求线段的数量,体现了数形结合的思想.
三.解答题(共7小题)
14.请你先动笔在草稿纸上画一画,再回答下列问题:
(1)平面内两条直线,可以把平面分成几部分?
(2)平面内3条直线,可以把平面分成几部分?
(3)平面内4条直线,可以把平面最多分成多少部分?
(4)平面内100条直线,可以把平面最多分成多少部分?
考点:直线、射线、线段.
专题:规律型.
分析:(1)(2)(3)这根据题意画图即可;
(4)根据(1)(2)(3)的数值得出规律,再根据规律解题.
解答:解:(1)如下图:可分成3个或4个平面;
(2)如下图:可分成4,6,7个平面;
(3)如下图:最可多分成11个.
(4)如图:一条直线可以把平面分成两部分,两条直线最多可以把平面分成4部分,三条直线最多可以把平面分成7部分,四条直线最多可以把平面分成11部分,可以发现,两条直线时多了2部分,三条直线比原来多了3部分,四条直线时比原来多了4部分,…,n条时比原来多了n部分.
因为n=1,a1=1+1,
n=2,a2=a1+2,
n=3,a3=a2+3,
n=4,a4=a3+4,
…
n=n,an=an﹣1+n,
以上式子相加整理得,an=1+1+2+3+…+n=1+.
100个时可分成1+=1+5050=5051.
点评:本题考查了直线射线和线段,要知道从一般到具体的探究方法,并找到规律.
15.指出下列句子的错误,并加以改正:
(1)如图1,在线段AB的延长线上取一点C;
(2)如图2,延长直线AB,使它与直线CD相交于点P;
(3)如图3,延长射线OA,使它和线段BC相交于点D.
考点:直线、射线、线段.
分析:(1)利用延长线的方向确定字母循序;
(2)直线无法延长,直接利用直线相交得出即可;
(3)应反向延长射线OA,得出即可.
解答:解:(1)如图1,应为:在线段BA的延长线上取一点C;
(2)如图2,应为:直线AB与直线CD相交于点P;
(3)如图3,反向延长射线OA,使它和线段BC相交于点D.
点评:此题主要考查了直线、射线、线段的定义,正确把握相关定义是解题关键.
16.用适当语句表述图中点与直线的关系:
考点:直线、射线、线段.
分析:(1)根据直线的位置关系以及点与直线的位置关系即可解答;
(2)直线a、b、c两两相交,再说明交点即可
解答:解:图1,直线l经过点A、B,点P在直线l外;
图2,直线a、b、c两两相交,直线a与直线c交于点C,直线a与直线b交于点B,直线b与直线c交于点A.
点评:本题主要考查了几何作图,注意叙述要准确.
17.阅读下表:
线段AB上的点数n(包括A、B两点)
图例
线段总条数N
3
3=2+1
4
6=3+2+1
5
10=4+3+2+1
6
15=5+4+3+2+1
7
解答下列问题:
(1)在上表中空白处分别画出图形,写出结果;
(2)写出线段的总条数N与线段上的点数n的关系式;
(3)试证明:N= .
考点:直线、射线、线段.
专题:规律型.
分析:(1)根据图中规律画出图形,写出结果;
(2)线段的总条数N与线段上的点数n的关系式N= ;
(3)由(1)的规律证明.
解答:解:(1)如图;
(2)N= ;
证明:(3)线段上有3个点时,线段总条数是3条,则3=1+2,
线段上有4个点时,线段总条数是6条,则6=3+2+1,
线段上有5个点时,线段总条数是10条,则10=4+3+2+1,
故线段上有n个点时,线段总条数(n﹣1)+…+3+2+1,则N= .
点评:此题在线段的基础上,着重培养学生的观察、实验和猜想、归纳能力,掌握从特殊向一般猜想的方法.
18.实践与应用:
一个西瓜放在桌子上用刀切下去,一刀可以切成2块,2刀最多可以切成4块;3刀最多可以切成7块,4刀最多可以切成11块(如图).
上述问题转化为数学模型实际上就是n条直线最多把平面分成几块的问题,有没有规律呢?请先进行试验,然后回答以下问题.
(1)填表:
(2)设n条直线把平面最多分成的块数是S,请写出S关于n的表达式.(不需要解题过程)
考点:直线、射线、线段.
专题:规律型.
分析:可以发现,两条直线时比原来多了2块,三条直线比原来多了3块,四条直线时比原来多了4块,…,n条时比原来多了n块,
∴n=1,S1=1+1
n=2,S2=S1+2
n=3,S3=S2+3
n=4,S4=S3+4
…
n=n,Sn=Sn﹣1+n
以上式子相加整理得,Sn=1+1+2+3+…+n=1+.
解答:解:(1)n=5,S5=1+1+2+3+4+5=16,
n=6,S6=1+1+2+3+4+5+6=22;
(2)Sn=1+1+2+3+…+n=1+.
点评:本题是找规律题,解题的关键是找到Sn=1+1+2+3+…+n=1+.
19.为了探究n条直线能把平面最多分成几部分,我们从最简单的情形入手.
(1)一条直线把平面分成2部分;
(2)两条直线最多可把平面分成4部分;
(3)三条直线最多可把平面分成11部分…;
把上述探究的结果进行整理,列表分析:
直线条数
把平面分成部分数
写成和形式
1
2
1+1
2
4
1+1+2
3
7
1+1+2+3
4
11
1+1+2+3+4
…
…
…
(1)当直线条数为5时,把平面最多分成 16 部分,写成和的形式 1+1+2+3+4+5 ;
(2)当直线为10条时,把平面最多分成 56 部分;
(3)当直线为n条时,把平面最多分成 +1 部分.(不必说明理由)
考点:直线、射线、线段.
专题:图表型.
分析:根据表中数据,总结出规律,再根据规律解题.
解答:解:(1)根据表中规律,当直线条数为5时,把平面最多分成16部分,1+1+2+3+4+5=16;
(2)根据表中规律,当直线为10条时,把平面最多分成56部分,为1+1+2+3+…+10=56;
(3)设直线条数有n条,分成的平面最多有m个.
有以下规律:
n m
1 1+1
2 1+1+2
3 1+1+2+3
:
:
:
n m=1+1+2+3+…+n=+1.
点评:本题体现了由“特殊到一般再到特殊”的思维过程,有利于培养同学们的探究意识.
20.观察下列图形,并阅读图形下面的相关文字:
猜想:
(1)5条直线相交最多有几个交点?
(2)6条直线相交最多有几个交点?
(3)n条直线相交最多有几个交点?
考点:直线、射线、线段.
专题:规律型.
分析:先观察图形,找出交点的个数与直线的条数之间的关系,然后进行计算即可.
解答:解:解:①5条直线相交最多有=10个交点;
②6条直线相交最多有=15个交点;
③n条直线相交最多有个交点.
点评:此题考查了相交线,关键是观察图形,找出规律,用到的知识点是同一平面内内n条直线相交最多有个交点.
