江苏省2024届高三上学期中秋金卷 数学(PDF版含解析)
文档属性
| 名称 | 江苏省2024届高三上学期中秋金卷 数学(PDF版含解析) |  | |
| 格式 | |||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-22 15:34:49 | ||
图片预览




文档简介
江苏省2024年高三年级上学期
中秋金卷
一、单选题
1.己知集合A={x(x+3(x-)<0},B={x2>1,则AnB=()
A.(-3,+w)B.(0,
C.(3,0)
D.(-0,)
2.已知i是虚数单位,复数(1+2)的共轭复数虚部为
A.4i
B.3
C.4
D.4
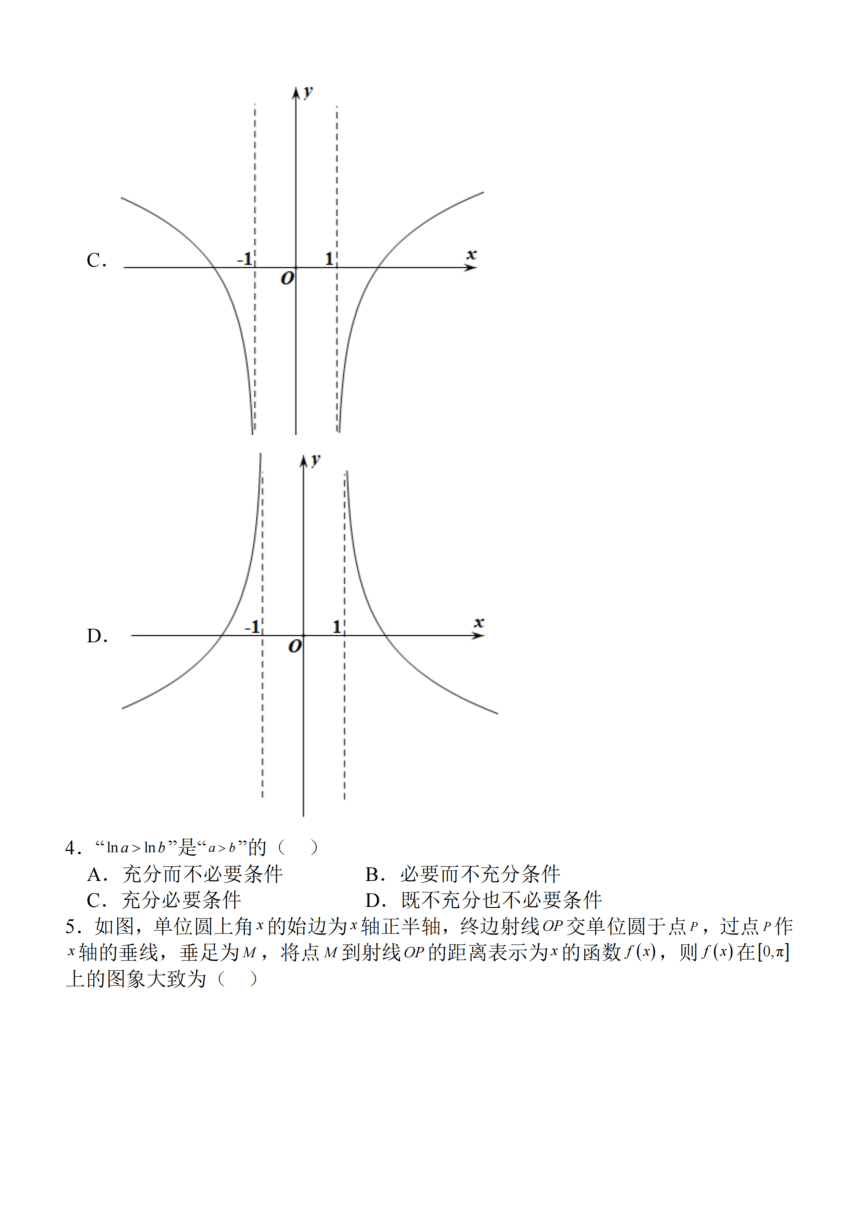
3.若函数f(x)=(a>0且a≠1)在R上为增函数,则函数y=logx-)的图象可以是
()
木y
A.
0
B
-1
1
式
C.
-1
-3E
1
4.“na>nb”是“a>b的()
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
5.如图,单位圆上角x的始边为x轴正半轴,终边射线OP交单位圆于点P,过点P作
x轴的垂线,垂足为M,将点M到射线OP的距离表示为x的函数f(x),则∫(x)在[O,π]
上的图象大致为()
B
π无
π
0x=0
6.已知函数()=n,x0’则下列选项正确的是()
A.f(x)没有极值点
B.当m∈(-1,)时,函数f(x)图象与直线y=m有三个公共点
C.点(1,0)是曲线y=f(x)的对称中心
D.直线y=x-1是曲线y=f(x)的切线
7.设a=n3,b=T,
=令,c=m名,则a,b,c之间的大小关系是()
A.a>b>c
B.a>c>b
C.b>c>a
D.c>b>a
og,x>0)’若方程倒=a有四个不同的解x,戏且<西<头x+1(x,0)
8.已知函数f(x)=
则x(+)+x的取值范围是()
A.(-l,+0)
B.别
c.(m到
D.(
二、多选题
9.己知是虚数单位,下列说法正确的是()
A.若复数满足z2∈R,则z∈R
B.若复数:满足z∈R,则EeR
C.若复数:品,则的值为:
D.若复数:满足+=-3列,则的最小值为1
10.设a>0,b>0,下列等式恒成立的是()
A.a3.a=a
43
B.a.a5=0
c.
35
116
D.aibi=ab
11.已知f(x)是定义在[-3,3]上的奇函数,f(A.f(0)=0B.f(0)C.f(-1)>f(-2)D.f(I)12.己知函数y=me的图象与直线y=x+2m有两个交点,则m的取值可以是()
A.-1
B.1
C.2
D.3
三、填空题
13.若a+a<0,则a2,a,-a2,-a由大到小排列顺序是
14.若“3x∈[1,2],使2x2-x+1<0成立”是假命题,则实数的取值范围是
15.已知某种果蔬的有效保鲜时间y(单位:小时)与储藏温度x(单位:℃)近似
满足函数关系y=eb(a,b为常数,e为自然对数底数),若该果蔬在7C的保鲜时
间为216小时,在28C的有效保鲜时间为8小时,那么在14C时,该果蔬的有效
保鲜时间大约为
小时
16.
设函数f(x)=
2x-1,x≤1
/(x-,x>1,8()=lg,则函数F()=f()-g()零点的个数有
个
四、解答题
17.已知4--6x+8≤B={号,C-纯ssa+号。
(1)求AnB;
(2)若AcC,求实数a的取值范围
18.若函数f(x)是定义在(-1,)上的奇函数,且在(0,1)上递增,解关于4的不等
式f(a-2)+f(a2-4)<0
19.己知二次函数f(x)=ax2+bx满足(①f(2)=0,②关于x的方程f(x)=x有两个相等的
实数根.
(1)求函数f)的解析式:
(2)求函数f)在[0,3]上的最大值.
20.已知函数f(x)=x+2xlnx.
(1)若直线1过点(0,-2),且与曲线y=(x)相切,求直线1的方程;
(2)若x>1时,f(x)-+k>0成立,求整数k的最大值.
21.己知函数f(x)=xcosx
(1)当x∈(0,π)时,求证:f(x)(2)证明:()=f(x)在0上单调递减:
(3)求证:当xe0,)时,方程f)-20有且仅有2个实数根,
22.己知函数f(x)=hx+am-ax2(aeR).
(1)若x=1是函数y=f(x)的极值点,求a的值:
(2)求函数y=∫(x)的单调区间,
中秋金卷
一、单选题
1.己知集合A={x(x+3(x-)<0},B={x2>1,则AnB=()
A.(-3,+w)B.(0,
C.(3,0)
D.(-0,)
2.已知i是虚数单位,复数(1+2)的共轭复数虚部为
A.4i
B.3
C.4
D.4
3.若函数f(x)=(a>0且a≠1)在R上为增函数,则函数y=logx-)的图象可以是
()
木y
A.
0
B
-1
1
式
C.
-1
-3E
1
4.“na>nb”是“a>b的()
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
5.如图,单位圆上角x的始边为x轴正半轴,终边射线OP交单位圆于点P,过点P作
x轴的垂线,垂足为M,将点M到射线OP的距离表示为x的函数f(x),则∫(x)在[O,π]
上的图象大致为()
B
π无
π
0x=0
6.已知函数()=n,x0’则下列选项正确的是()
A.f(x)没有极值点
B.当m∈(-1,)时,函数f(x)图象与直线y=m有三个公共点
C.点(1,0)是曲线y=f(x)的对称中心
D.直线y=x-1是曲线y=f(x)的切线
7.设a=n3,b=T,
=令,c=m名,则a,b,c之间的大小关系是()
A.a>b>c
B.a>c>b
C.b>c>a
D.c>b>a
og,x>0)’若方程倒=a有四个不同的解x,戏且<西<头
8.已知函数f(x)=
则x(+)+x的取值范围是()
A.(-l,+0)
B.别
c.(m到
D.(
二、多选题
9.己知是虚数单位,下列说法正确的是()
A.若复数满足z2∈R,则z∈R
B.若复数:满足z∈R,则EeR
C.若复数:品,则的值为:
D.若复数:满足+=-3列,则的最小值为1
10.设a>0,b>0,下列等式恒成立的是()
A.a3.a=a
43
B.a.a5=0
c.
35
116
D.aibi=ab
11.已知f(x)是定义在[-3,3]上的奇函数,f(
A.-1
B.1
C.2
D.3
三、填空题
13.若a+a<0,则a2,a,-a2,-a由大到小排列顺序是
14.若“3x∈[1,2],使2x2-x+1<0成立”是假命题,则实数的取值范围是
15.已知某种果蔬的有效保鲜时间y(单位:小时)与储藏温度x(单位:℃)近似
满足函数关系y=eb(a,b为常数,e为自然对数底数),若该果蔬在7C的保鲜时
间为216小时,在28C的有效保鲜时间为8小时,那么在14C时,该果蔬的有效
保鲜时间大约为
小时
16.
设函数f(x)=
2x-1,x≤1
/(x-,x>1,8()=lg,则函数F()=f()-g()零点的个数有
个
四、解答题
17.已知4--6x+8≤B={号,C-纯ssa+号。
(1)求AnB;
(2)若AcC,求实数a的取值范围
18.若函数f(x)是定义在(-1,)上的奇函数,且在(0,1)上递增,解关于4的不等
式f(a-2)+f(a2-4)<0
19.己知二次函数f(x)=ax2+bx满足(①f(2)=0,②关于x的方程f(x)=x有两个相等的
实数根.
(1)求函数f)的解析式:
(2)求函数f)在[0,3]上的最大值.
20.已知函数f(x)=x+2xlnx.
(1)若直线1过点(0,-2),且与曲线y=(x)相切,求直线1的方程;
(2)若x>1时,f(x)-+k>0成立,求整数k的最大值.
21.己知函数f(x)=xcosx
(1)当x∈(0,π)时,求证:f(x)
(3)求证:当xe0,)时,方程f)-20有且仅有2个实数根,
22.己知函数f(x)=hx+am-ax2(aeR).
(1)若x=1是函数y=f(x)的极值点,求a的值:
(2)求函数y=∫(x)的单调区间,
同课章节目录
