异面直线所成的角(河南省郑州市)

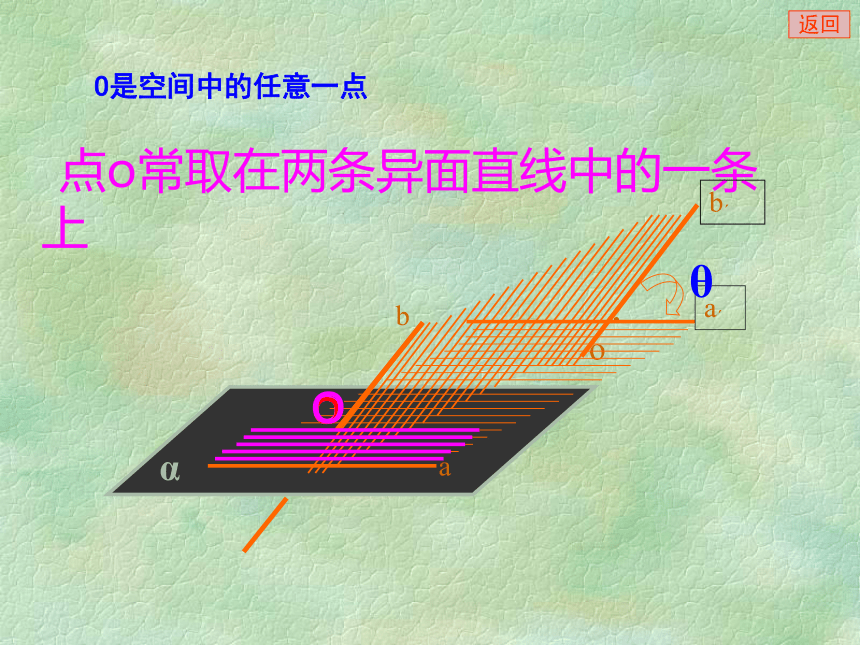
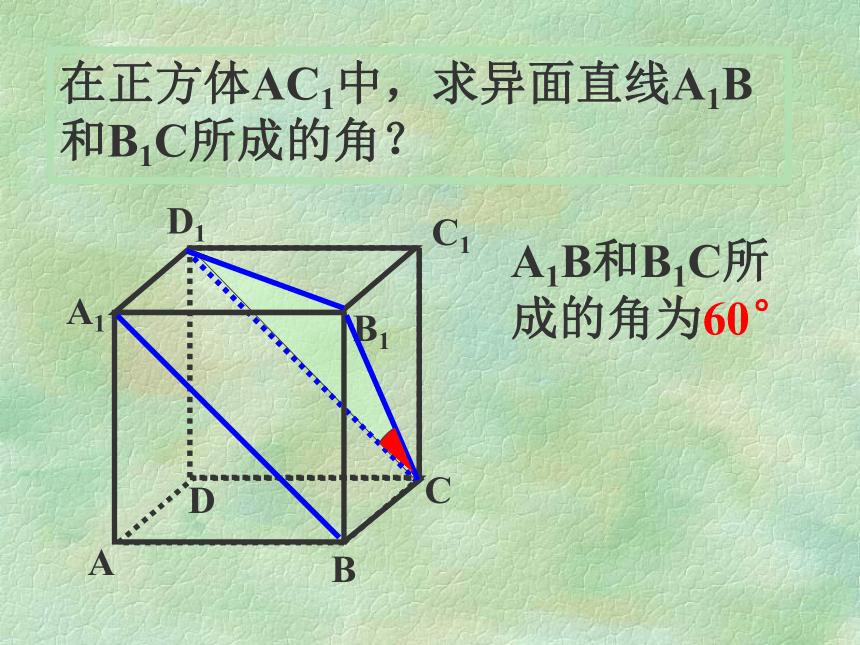
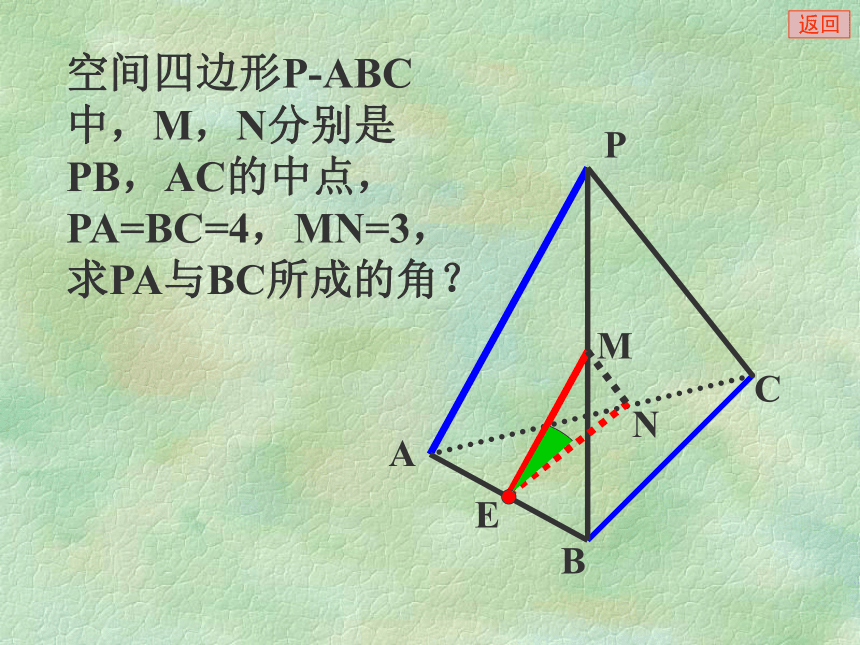
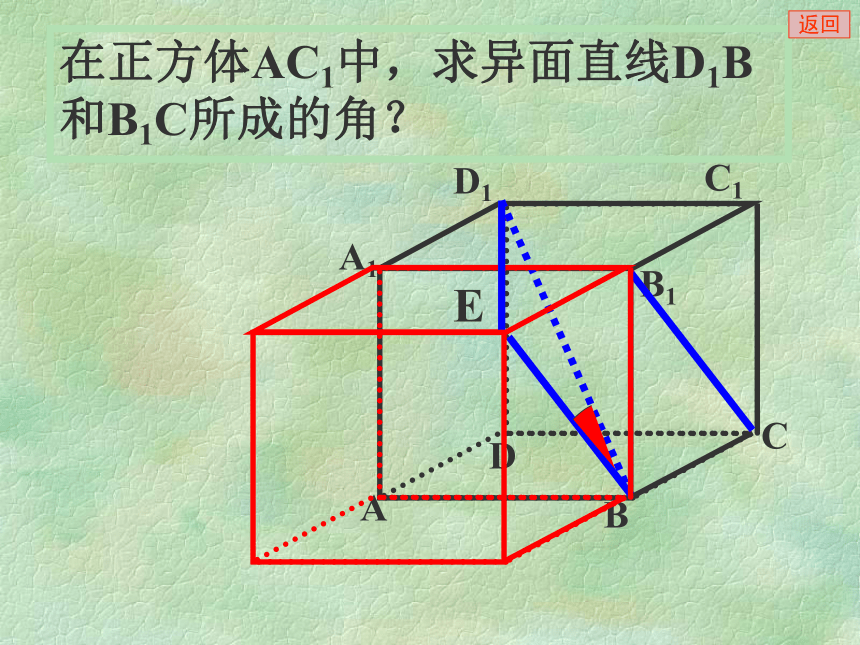
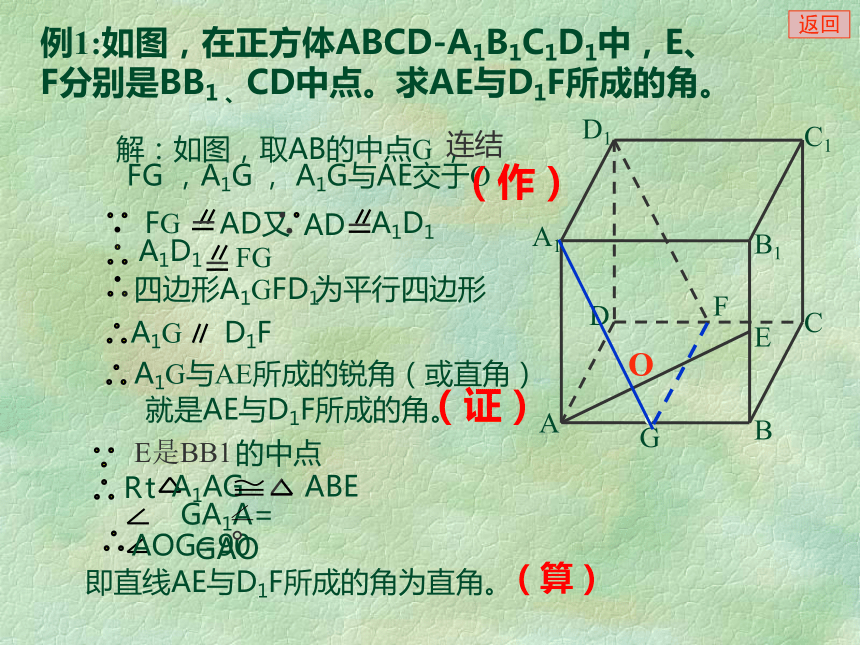
课件20张PPT。 异面直线所成的角 对于两条异面直线a、b ，经过空间任意一点o，作直线a’//a，b’//b，则直线a’和b’所成的锐角（或直角）叫做异面直线a和b所成的角。两条异面直线所成的角两条异面直线所成的角的范围是（0， ]aαbO是空间中的任意一点 点o常取在两条异面直线中的一条上θooooo返回二、数学思想、方法、步骤：转化与化归，即把异面直线所成的角（空间角）转化为平面角，进而转化为三角形的内角，然后通过解三角形求得.2.方法： 3.步骤： ①作（找）② 证③ 计算1.数学思想：平移可解三角形在正方体AC1中，求异面直线A1B和B1C所成的角？A1B和B1C所成的角为60°PABCMN空间四边形P-ABC中，M，N分别是PB，AC的中点，PA=BC=4，MN=3，求PA与BC所成的角？返回在正方体AC1中，求异面直线D1B和B1C所成的角？ABDCA1B1D1C1返回A1ABB1CDC1D1FE解：如图，取AB的中点G ，O（证）（作）例1:如图，在正方体ABCD-A1B1C1D1中，E、F分别是BB1 、CD中点。求AE与D1F所成的角。返回（算）例2 在棱长都相等的四面体A-BCD中，M、N分别是棱AD、BC 的中点，
连结AN、CM，求异面直线AN、CM所成的角的余弦值。例2已知正方体的棱长为 a , M 为 AB 的中点, N 为 BB1的中点，求 A1M 与 C1 N 所成角的余弦值。解：EG如图，取AB的中点E, 连BE, 有BE∥ A1M 取CC1的中点G,连BG. 有BG∥ C1N 则∠EBG即为所求角。BG=BE= a, F C1 = a由余弦定理，cos∠EBG=2/5F取EB1的中点F，连NF,有BE∥NF则∠FNC为所求角。想一想：还有其它定角的方法吗？在△EBG中例3：长方体ABCD-A1B1C1D1，AB=AA1=2 cm， AD=1cm，求异面直线A1C1与BD1所成角的余弦值。返回解法二：方法归纳：补形法把空间图形补成熟悉的或完整的几何体，如正方体、长方体等，其目的在于易于发现两条异面直线的关系。 在?A1C1E中，由余弦定理得?A1C1与BD1所成角的余弦值为 如图，补一个与原长方体全等的并与原长方体有公共面连结A1E，C1E，则?A1C1E为A1C1与BD1所成的角(或补角)，BC1的长方体B1F，返回1： 如图，在正方体 ABCD－A1B1C1D1中，异面直线AC与BC1所成角的大小是（ ）．
A．30° B．45° C．60° D．90°返回热身训练2： 如图，正三棱锥S－A BC的侧棱与底面边长相等，如果E、F分别为SC、 A B的中点，那么异面直线EF与SA所成角等于（ ） A．90° B．60° C．45° D．30°返回解：取AC的中点G，连接EG、FG，
∵ EG//SA，∴ ∠GEF是异面直线EF与SA所成角，又FG//BC，SA⊥BC，
∴ ∠EGF=90°，
△EGF是直角三角形，又EG=SA，FG=BC，
∴ EG=FG，△EGF是等腰直角三角形，
∴ ∠GEF=45°，选C.返回
正方体ABCD- A1B1C1D1中,AC、BD交于O,则OB1与A1C1所成的角的度数为课堂练习：1900返回在正四面体S-ABC中，SA⊥BC, E, F分别为SC、AB 的中点，那么异面直线EF 与SA 所成的角等于（ ）CD(A)300 (B)450 (C)600 (D)900练习2B返回2.已知：两异面直线a,b所成的角是50 °，P为
空间中一定点，则过点P且与a,b都成30°角的
直线有 条。abPO2返回定角一般方法有：（1）平移法（常用方法）小结：1、求异面直线所成的角是把空间角转化为平面 角，体现了化归的数学思想。2、用余弦定理求异面直线所成角时，要注意角的 范围： （1） 当 cosθ ＞ 0 时，所成角为 θ（2） 当 cosθ ＜ 0 时，所成角为π－ θ（3） 当 cosθ = 0 时，所成角为 90o（2）补形法化归的一般步骤是：定角求角返回说明：异面直线所成角的范围是（0， ]，在把异面直线所成的角平移转化为平面三角形中的角，常用余弦定理求其大小，当余弦值为负值时，其对应角为钝角，这不符合两条异面直线所成角的定义，故其补角为所求的角，这一点要注意。 返回