4.2光的全反射 讲义

中小学教育资源及组卷应用平台
4.2 光的全反射
一、考点梳理
考点一、全反射
1．发生全反射的条件
(1)光从光密介质射至光疏介质．
(2)入射角大于或等于临界角．
以上两个条件缺一不可．
2．全反射遵循的规律
发生全反射时，光全部返回原介质，入射光与反射光遵循光的反射定律，由于不存在折射光线，光的折射定律不再适用.
3．全反射棱镜改变光路的几种情况
入射方式项目 方式一 方式二 方式三
光路图
入射面 AB AC AB
全反射面 AC AB、BC AC
光线方向改变角度 90° 180° 0°(发生侧移)
【典例1】如图所示，直角三角形ABC为一透明介质制成的三棱镜截面，且∠BAC＝30°，有一束平行光线垂直射向AC面．已知这种介质的折射率n＞2，则(　　)
A．可能有光线垂直于AB边射出
B．光线只能从BC边垂直射出
C．光线只能从AC边垂直射出
D．一定既有光线垂直于BC边射出，又有光线垂直于AC边射出
【答案】D
【解析】因n＞2，而sin C＝，所以sin C<，即C＜30°，射到AB边的入射角i＝30°，发生了全反射．此光线反射后射到AC边的入射角i＝60°，再次发生全反射而垂直射到BC边上射出．同理，射到BC边上的光线，经两次全反射后垂直AC射出．
【典例2】2.(多选)白光是由多种单色光构成的复合光,点光源S发出的一束白光由空气斜射到横截面为矩形acdb的玻璃砖上的O点,S、O和d三点位于同一直线上,θ为入射角,如图所示,下列说法正确的是(　　)　　　　　
A.当θ增大时,光不可能在ab界面上发生全反射
B.当θ增大时,光可能射到bd界面上,但不可能在bd界面上发生全反射
C.射到cd界面上的光,一定不能在cd界面上发生全反射
D.从cd界面射出的各种色光一定互相平行
【答案】ACD
【解析】白光由空气斜射入玻璃砖是由光疏介质射向光密介质,不可能在ab界面上发生全反射,A正确;当θ增大时,折射角增大,光可能射到bd界面上,若在bd界面的入射角大于临界角,可能发生全反射,故B错误;由于光在cd面的入射角等于ab面的折射角,根据光路的可逆性知,光在cd面的出射角等于在ab面的入射角,光不可能在cd面上发生全反射,并且从cd界面射出的各种色光一定互相平行,C、D正确。
练习1、(多选)如图所示，半圆形玻璃砖放在空气中，三条同一颜色、强度相同的光线，均由空气沿半圆半径方向射入玻璃砖，到达玻璃砖的圆心位置．下列说法正确的是(　　)
A．假若三条光线中只有一条在O点发生了全反射，那一定是aO光线
B．假若光线bO能发生全反射，那么光线cO一定能发生全反射
C．假若光线bO能发生全反射，那么光线aO一定能发生全反射
D．假若光线aO恰能发生全反射，那么光线bO的反射光线比光线cO的反射光线的亮度大
【答案】ACD
【解析】在玻璃砖直径界面，光线aO的入射角最大，光线cO的入射角最小，它们都是从光密介质射向光疏介质，都有发生全反射的可能．如果只有一条光线发生了全反射，那一定是aO光线，因为它的入射角最大，所以选项A对；假若光线bO能发生全反射，说明它的入射角等于或大于临界角，光线aO的入射角更大，所以，光线aO一定能发生全反射，光线cO的入射角可能大于或等于临界角，也可能小于临界角，因此，光线cO不一定能发生全反射，所以选项B错，C对；假若光线aO恰能发生全反射，则光线bO和光线cO都不能发生全反射，但光线bO的入射角更接近于临界角，所以，光线bO的反射光线较光线cO的反射光线强，即光线bO的反射光线亮度较大，所以D对．
练习2、(多选)已知水、水晶、玻璃和二硫化碳的折射率分别为1.33、1.55、1.60和1.63,如果光按以下几种方式传播,可能发生全反射的是(　　)
A.从玻璃射入水晶 B.从水射入二硫化碳
C.从玻璃射入水中 D.从水晶射入水
E.从玻璃射入二硫化碳
【答案】ACD
【解析】发生全反射的条件之一是光从光密介质射入光疏介质,光密介质折射率较大,光疏介质折射率较小,故A、C、D正确。
练习3、自行车上的红色尾灯不仅是装饰品，也是夜间骑车的安全指示灯，它能把来自后面的光照反射回去．某种自行车尾灯可简化为由许多整齐排列的等腰直角棱镜(折射率n>)组成，棱镜的横截面如图所示．一平行于横截面的光线从O点垂直AB边射入棱镜，先后经过AC和CB边反射后，从AB边的O′点射出，则出射光线是(　　)
A．平行于AC边的光线①
B．平行于入射光线的光线②
C．平行于CB边的光线③
D．沿AB边的光线④
【答案】B
【解析】由题意可知，折射率n>，且sin C＝，得临界角小于45°，由题图可得，光从空气进入棱镜．因入射角为0°，所以折射光线不偏折．当光从棱镜射向空气时，入射角等于45°，发生全反射，根据几何关系，结合光路可逆可知，出射光线是②，即平行于入射光线，故B正确，A、C、D错误．
考点二、全反射的应用
1．光导纤维
如图所示是光导纤维的结构示意图，其内芯和外套由两种光学性能不同的介质构成．构成内芯和外套的两种介质中，内芯的折射率大．因为当内芯的折射率大于外套的折射率时，光在传播时能发生全反射，光线经过多次全反射后能从一端传到另一端．
2．解决全反射问题的思路
(1)确定光是由光疏介质进入光密介质还是由光密介质进入光疏介质．
(2)若光由介质进入空气(真空)时，则根据sin C＝确定临界角，看是否发生全反射．
(3)根据题设条件，画出入射角等于临界角的“临界光路”．
(4)运用几何关系、三角函数关系、反射定律等进行判断推理，运算及变换进行动态分析或定量计算．
【典例1】（单选）自行车尾灯采用了全反射棱镜的原理,它虽然本身不发光,但在夜间行驶时,从后面开来的汽车发出的强光照在尾灯上,会有较强的光被反射回去,使汽车司机注意到前面有自行车。尾灯由透明介质做成,其外形如图所示。下列说法中正确的是(　　)
A.汽车灯光应从左面射过来,在尾灯的左表面发生全反射
B.汽车灯光应从左面射过来,在尾灯的右表面发生全反射
C.汽车灯光应从右面射过来,在尾灯的右表面发生全反射
D.汽车灯光应从右面射过来,在尾灯的左表面发生全反射
【答案】D
【解析】自行车尾灯利用了全反射棱镜原理,汽车灯光应从右面射过来,在左表面的直角边上发生两次全反射被反射回去。
【典例2】如图所示，AB为光导纤维，A、B之间距离为s，使一光脉冲信号从光导纤维中间入射，射入后在光导纤维与空气的界面上恰好发生全反射，由A点传输到B点所用时间为t，求光导纤维所用材料的折射率n.(已知光在真空中的传播速度为c)
【答案】
【解析】设光导纤维所用材料的折射率为n，则有sin α＝sin C＝
n＝ ，t＝＝
由以上三式解得t＝＝ ，所以n＝
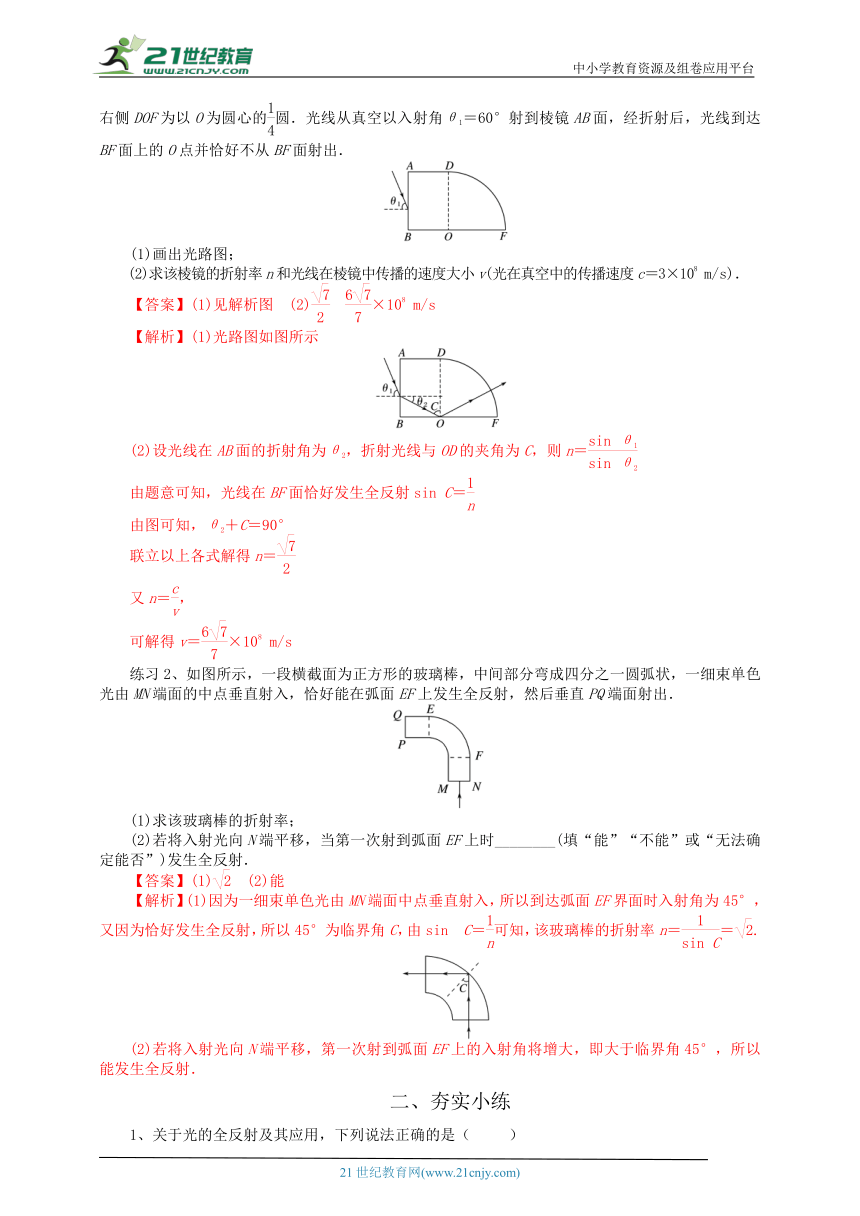
练习1、用某种透明材料制成的一块柱体形棱镜的水平截面图如图所示，左侧ABOD为长方形，右侧DOF为以O为圆心的圆．光线从真空以入射角θ1＝60°射到棱镜AB面，经折射后，光线到达BF面上的O点并恰好不从BF面射出．
(1)画出光路图；
(2)求该棱镜的折射率n和光线在棱镜中传播的速度大小v(光在真空中的传播速度c＝3×108 m/s)．
【答案】(1)见解析图　(2)　×108 m/s
【解析】(1)光路图如图所示
(2)设光线在AB面的折射角为θ2，折射光线与OD的夹角为C，则n＝
由题意可知，光线在BF面恰好发生全反射sin C＝
由图可知，θ2＋C＝90°
联立以上各式解得n＝
又n＝，
可解得v＝×108 m/s
练习2、如图所示，一段横截面为正方形的玻璃棒，中间部分弯成四分之一圆弧状，一细束单色光由MN端面的中点垂直射入，恰好能在弧面EF上发生全反射，然后垂直PQ端面射出．
(1)求该玻璃棒的折射率；
(2)若将入射光向N端平移，当第一次射到弧面EF上时________(填“能”“不能”或“无法确定能否”)发生全反射．
【答案】(1)　(2)能
【解析】(1)因为一细束单色光由MN端面中点垂直射入，所以到达弧面EF界面时入射角为45°，又因为恰好发生全反射，所以45°为临界角C，由sin C＝可知，该玻璃棒的折射率n＝＝.
(2)若将入射光向N端平移，第一次射到弧面EF上的入射角将增大，即大于临界角45°，所以能发生全反射．
二、夯实小练
1、关于光的全反射及其应用，下列说法正确的是（ ）
A.入射角大于临界角，光一定发生全反射
B.光从传播速度大的介质射向传播速度小的介质时可能发生全反射
C.光导纤维传输信号和全息照相利用的都是光的全反射现象
D.水或玻璃中的气泡看起来特别亮，是因为光从水或玻璃射向气泡时在界面发生了全反射
【答案】D
【解析】A．入射角大于临界角，不一定发生全反射，还要光从光密介质进入光疏介质才能发生全反射，A不符合题意；
B．当光线从从光密介质进入光疏介质时才有可能发生全反射，由n= 可知，光在介质中的传播速度越大，介质折射率越小，光在介质中传播速度越小，介质的折射率越大，即光从传播速度大的介质射向传播速度小的介质时不可能发生全反射，B不符合题意；
C．光导纤维传输信号是利用光的全反射现象，全息照相是利用了激光相干性好的特性，运用了光的干涉现象，C不符合题意；
D．当光线由水或玻璃射向气泡时，由于水和玻璃的折射率均大于空气的折射率，部分光线在界面处发生全反射，所以气泡看起来特别亮，D符合题意。
2、下列现象中属于光的全反射现象的是 （ ）
A.阳光照射存肥皂泡上,常看到肥皂泡上有彩色花纹
B.玻璃中的气泡,有时看上去特别明亮
C.在阳光下用白纸对着凹镜前后移动时,在一定距离处纸上会出现耀眼的光斑
D.飞机在阳光下作特技飞行时,有时会看到飞机突然变得非常明亮
【答案】 B
【解析】A．在阳光照射下，常看到肥皂泡上有彩色花纹是由于薄膜干涉现象产生的，A不符合题意；
B．玻璃中的气泡有时看上去特别明亮，是由于光从玻璃射入气泡时发生全反射形成的，B符合题意；
C．在阳光下用白纸对着凸镜前后移动时，在一定距离处纸上会出现耀眼的光斑，这是光的折射现象，C不符合题意；
D．飞机在阳光下作特技飞行时，有时会看到飞机变得非常明亮，是由于光的反射形成的，D不符合题意．
3、如图所示，一足够大的水池内盛有某种透明液体，液体的深度为H，在水池的底部放一点光源S，其中一条光线以 入射角射到液体与空气的界面上，以折射角 发生折射。则（ ）
液体的折射率为 B.从液体到空气，光波长变短
C.液体表面亮斑的面积为 D.光线从液体到空气发生全反射时的临界角为45°
【答案】D
【解析】A．液体的折射率为
A不符合题意；
B．从液体到空气，频率和周期不变，波速变大，则由 可知，波长变长，B不符合题意；
CD．根据
则C=45°
即光线从液体到空气发生全反射时的临界角为45°，则液体表面亮斑的面积为
C不符合题意，D符合题意。
4、如图，在某种液体内，有一轴截面为正三角形的薄壁透明圆锥罩ABC，底面水平，罩内为空气。发光点D位于AB中点，发出的垂直于BC的光恰好不能射出液面。下列说法正确的是（ ）
A.D发出的光照射到CB界面时可能发生全反射
B.液面上方能够看到透明罩所有位置都被照亮
C.液体的折射率为
D.液体的折射率为
【答案】 C
【解析】A．D发出的光照射到CB界面时，是从光疏介质向光密介质入射，不能发生全反射，A不符合题意；
B．由题知，发光点D发出的垂直于BC的光恰好不能射出液面，可知点D发出的在垂直于BC以下的部分光不能射出液面，所以在液面上方不能够看到透明罩所有位置都被照亮，B不符合题意；
CD．由几何关系可知，发光点D发出的垂直于BC的光垂直于BC进入液体后，在上边的液面处的入射角等于 ，恰好不能射出液面，则临界角为 ，所以折射率
5、2009年诺贝尔物理学奖授予英国华裔物理学家高锟，以表彰他在光纤通信研究中的突出贡献。光纤通信是利用了光的全反射的原理，光导纤维由内芯和外套两层组成。下列有关光导纤维的说法中正确的是（ ）
A.内芯的折射率比外套大，光传播时在内芯与外套的界面发生全反射
B.内芯的折射率比外套小，光传播时在内芯与外套的界面发生全反射
C.内芯的折射率比外套小，光传播时在内芯与外套的界面发生折射
D.内芯的折射率与外套相同，外套的材料有韧性，可以对内芯起保护作用
【答案】 A
【解析】全反射的条件是光从光密介质进入光疏介质，入射角大于等于临界角。所以内芯的折射率大于外套的折射率，光传播时在内芯和外套的界面上发生全反射，A符合题意．
6、一个半径为r的薄软木圆片，在它的圆心处插入一枚大头针．让它们浮在水面上，如图所示．调整大头针露出的长度，直至从水面上方的各个方向向水中看，都恰好看不到大头针，这是因为发生了________现象．若此时木片下方大头针的长度为h，则水的折射率为________．
【答案】全反射；
【解析】解：观察者在水面上各个方向都刚好看不到水下的大头针，说明由针头射出的光线，恰好在水面与木塞的边缘处发生全反射．
由题意作出光路图如图所示，这时入射角等于临界角，由几何关系可得
sinC=
又sinC=
由以上两式解得液体的折射率为
n= ．
故答案为：全反射，
7、如图所示，ABCD是一直角梯形棱镜的横截面，位于截面所在平面内的一束光线由O点垂直AD边射入。 已知棱镜的折射率 ，∠OAB=60°。求光从棱镜中射出的光线与CD边的夹角为多少度？
【答案】45°或135°。
【解析】当光从玻璃射向空气发生全反射时有
可知临界角为C=45°
根据几何关系可知光射在AB和BC面均会发生全反射
当光射到CD边时，由几何关系可知入射角i=30°
由折射定律有
解得r=45°
可知从棱镜射出的光线与CD边的夹角为45°或135°。
8、如图所示，某种透明介质的截面图由直角三角形AOC和圆心为O、半径为R的四分之一圆弧BC组成，其中∠A = 60°。一束单色光从D点垂直AB面射入透明介质中，射到圆弧BC上时恰好发生全反射．已知D点与O点之间的距离为 ，光在真空中的传播速度为c．求：
（i）单色光在介质中的传播速度v；
（ii）单色光第一次射出介质时折射角θ．
【答案】（i）
（ii）θ = 45°
【解析】（i）设介质的临界角为∠1，则
解得∠1 = 45°，
n =
折射率与速度的关系有
解得
（ii）EF与AB平行∠3 = 90° – ∠EFC = 90° – ∠A = 30°
根据折射定律有
解得θ = 45°
三、培优练习
1、（多选）如图所示为投影仪的镜头，是一个半球形的玻璃体。光源产生的单色平行光投射到玻璃体的平面上，经半球形镜头折射后在光屏MN上形成一个圆形光斑。已知镜头半径为R，光屏MN到球心O的距离为d(d＞3R)，玻璃对该单色光的折射率为n(n＞1.5)，则(　　)
A．平行光从玻璃体左侧平面入射时没有反射
B．进入玻璃体的光线可能在右侧球面发生全反射
C．光屏上被照亮的圆形光斑半径为d－nR
D．若继续增大d，则光屏上的光斑可能先减小后增大
【答案】BC
【解析】平行光从玻璃体左侧平面垂直入射，有反射也有折射，入射角为零，折射角、反射角也为零，故A错误；如图所示，假设光线入射到D点时恰好发生全反射，
sin C＝，OF＝＝
又因为＝tan C
O′F＝d－OF
解得：r＝d－nR，故B、C正确；如图所示，继续增大d，则光屏上的光斑会增大，故D错误。
2、如图所示，半球形玻璃的折射率为n，半径为R，平行单色光从下方射入，若要使第一次射到球面上的光不从球面上出射，可在半球形玻璃的圆形底面上放一个挡光屏，则该挡光屏的最小面积为（　　）
A． B． C． D．
【答案】B
【解析】假设光线入射到A、B反射，则由公式
则可知在半球形玻璃上，半径为x的圆形范围内的光都可以从球面射出，由图可知
则可得
则挡光屏的最小面积为
故B正确，A、C、D错误。
3、如图所示，空气中有一横截面为半圆环的均匀透明柱体，其内圆半径为r，外圆半径为R，R=r。现有一束单色光垂直于水平端面A射入透明柱体，只经过两次全反射就垂直于水平端面B射出。设透明柱体的折射率为n，光在透明柱体内传播的时间为t，若真空中的光速为c，则（　　）
A．n可能为 B．n可能为2
C．t可能为 D．t可能为
【答案】AB
【解析】AB．只经过两次全反射可知第一次入射角为45°，反射光路图如图所示：
根据全反射可知临界角
C≤45°
根据折射率
可知
n≥
故A、B正确；
CD．光在透明柱体中运动路程为
L=4r
运动时间为
则
t≥
故C、D错误。
4、如图所示是两个城市间光缆中的一条光导纤维的一段，光缆总长为L，它的玻璃芯的折射率为n1，外层材料的折射率为n2.若光在空气中的传播速度近似为c，则对于光由它的一端射入经多次全反射后从另一端射出的过程，下列判断中正确的是(　　)
A．n1B．n1C．n1>n2，光通过光缆的时间等于
D．n1>n2，光通过光缆的时间大于
【答案】D
【解析】光从光密介质射入光疏介质，才可能发生全反射，故n1>n2；光在内芯传播的路程s＝，光在内芯的传播速度v＝，所以t＝＝，故D正确．
5、一束光从AB面射入如图所示的透明三棱镜中，在三棱镜中的折射光线平行于BC面，折射光线射到AC面上时恰好发生全反射。求光从AB面进入透明三棱镜的入射角，并在图上画出该光在透明三棱镜中的光路图。
【解析】光在AC面恰好发生全反射，并垂直BC面射出，光路图如图所示

由图可知临界角C=45°，折射角r=30°
根据
解得
光从AB面进入透明三棱镜，由折射定律有
解得i=45°
6、一厚度为h的大平板玻璃水平放置，其下表面贴有一半径为r的圆形发光面．在玻璃板上表面放置一半径为R的圆纸片，圆纸片与圆形发光面的中心在同一竖直线上．已知圆纸片恰好能完全遮挡住从圆形发光面发出的光线(不考虑反射)，求平板玻璃的折射率．
【答案】
【解析】如图所示，从圆形发光面边缘的A点发出的一条光线射到玻璃板上表面A′点恰好发生全反射，
则有sin C＝
又由几何关系：sin C＝
其中L＝R－r
联立以上各式解得n＝＝.
7、如图所示，折射率n＝的半圆形玻璃砖置于光屏MN的上方，其平面AB与MN的距离h＝10 cm.一束单色光沿图示方向射向圆心O，经玻璃砖后射到光屏上的O′点．现使玻璃砖绕圆心O点顺时针转动，光屏上的折射光线光点距O′点的距离最远时，求：
(1)此时玻璃砖转过的角度；
(2)光屏上的折射光线光点距O′点的最远距离．
【答案】(1)　(2) cm
【解析】(1)如图，设玻璃砖转过α角时折射光线光点离O′点最远，记此时光点位置为A，此时光线在玻璃砖的平面上恰好发生全反射，临界角为C，由折射定律有sin C＝＝，
可得全反射的临界角C＝.
由几何关系知，α＝C＝，
此时玻璃砖转过的角度为.
(2)折射光线光点A到O′的距离为xAO′＝
解得xAO′＝ cm
8、如图所示，玻璃球的半径为R，球心为O，玻璃球的对称轴O1O2与足够大的屏幕垂直于O2点，O、O2两点间的距离为2R。一束单色光沿图示方向以入射角θ＝60°从O1射入球内，在屏上留下光斑P，若玻璃对该单色光的折射率为，求：
（1）玻璃对该单色光的全反射临界角的正弦值；
（2）光斑P到O2之间的距离。
【答案】（1）；（2）R
【解析】（1）设玻璃对该单色光的全反射临界角为C，则
（2）光路图如图所示
根据折射定律得
又
得
又
所以
P点与点间的距离为
9、在桌面上有一个倒立的玻璃圆锥，其顶点恰好与桌面相接触，圆锥的轴（图中虚线）与桌面垂直，过轴线的截面为等边三角形，如图所示，有一半径为r=0.1m的圆柱形平行光束垂直入射到圆锥的桌面上，光束的中心轴与圆锥的轴重合，已知玻璃的折射率为n=1.73．则
（1）通过计算说明光线1能不能在圆锥的侧面B点全反射；
（2）光线1经过圆锥侧面B点后射到桌面上某一点所用的总时间是多少？（结果保留三位有效数字）。
【答案】（1）能；（2）
【解析】（1）由可得
入射角等于临界角，所以光线1能在圆锥的侧面B点发生全反射。
（2）当半径为r的圆柱形平行光束垂直入射到圆锥的地面上，经过第一次折射时，由于入射角等于零，所以折射角也是零，因此折射光线不发生偏折，当第二次折射时，由于入射角等于60°，而玻璃的折射率为1.73，可得入射角与临界角相等，所以会发生光的全反射，反射光线却恰好垂直射出，作图如下
根据几何关系可知
所以，总时间
10、．图示为一截面为直角三角形ABC的棱镜，一条光线从D点垂直于BC由真空射向棱镜，已知棱镜材料对入射光的折射率为n＝，∠A＝30°，AB边的长度为8m，D点距离B点1m，真空中的光速为3×108m/s。求：
（1）在此截面所在的平面内，光线第一次射出棱镜的出射点的位置；
（2）光从D点进入棱镜到第一次射出棱镜所经历的时间。（不考虑光线沿原来路返回的情况，要求画出光路图，结果可用根号表示）
【答案】（1）m；（2）
【解析】（1）光路如图所示
因DE//AC，故
∠BED=∠A=30°
则E点的入射角
α=60°
根据临界角公式
sinC=
可得棱镜对入射光全反射的临界角
C=45°
因α>C，故光线在E点发生全反射。
F点的入射角β=30°，因βBEsin30°=BD
BE=2m，AE=AB-BE=6m
2AFcos30°=AE
解得
AF=m
（2）根据光在介质中的传播速度与光速的关系
n=
解得
v=m/s
DE=BEcos30°=m
EF=AF=m
则光在棱镜中的路程
x路=DE+EF=m
则光从D点进入棱镜到第一次射出棱镜所经历的时间
t==
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)