12.3角的平分线的性质 同步练习(含答案) 2023-2024学年人教版数学八年级上册
文档属性
| 名称 | 12.3角的平分线的性质 同步练习(含答案) 2023-2024学年人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 198.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-23 18:10:04 | ||
图片预览

文档简介
12.3角的平分线的性质 同步练习 2023-2024学年人教版数学八年级上册
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.用尺规作角平分线的依据是( )
A.SAS B.ASA C.AAS D.SSS
2.已知∠AOB=80°,∠BOC=30°,OM平分∠ AOB, ON平分∠AOC则∠MON的度数为( )
A.15° B.15°或55° C.30°或110° D.30°或55°
3.在△ABC中,∠ABC与∠ACB的平分线相交于O,则∠BOC一定( )
A.大于90° B.等于90°
C.小于90° D.小于或等于90°
4.如图△BAC中,∠C=90°,AD是角平分线,DE⊥AB于E,且BC=5cm,BD=3cm,则DE等于( )
A.2cm B.3cm C.4cm D.5cm
5.如图,OP平分∠AOB,PC⊥OA于C,点D是OB上的动点,若PC=6cm,则PD的长可以是( )
A.7cm B.4cm C.5cm D.3cm
6.如图,AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE、CF相交于点D,则①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.以上结论正确的是( )
A.① B.② C.①② D.①②③
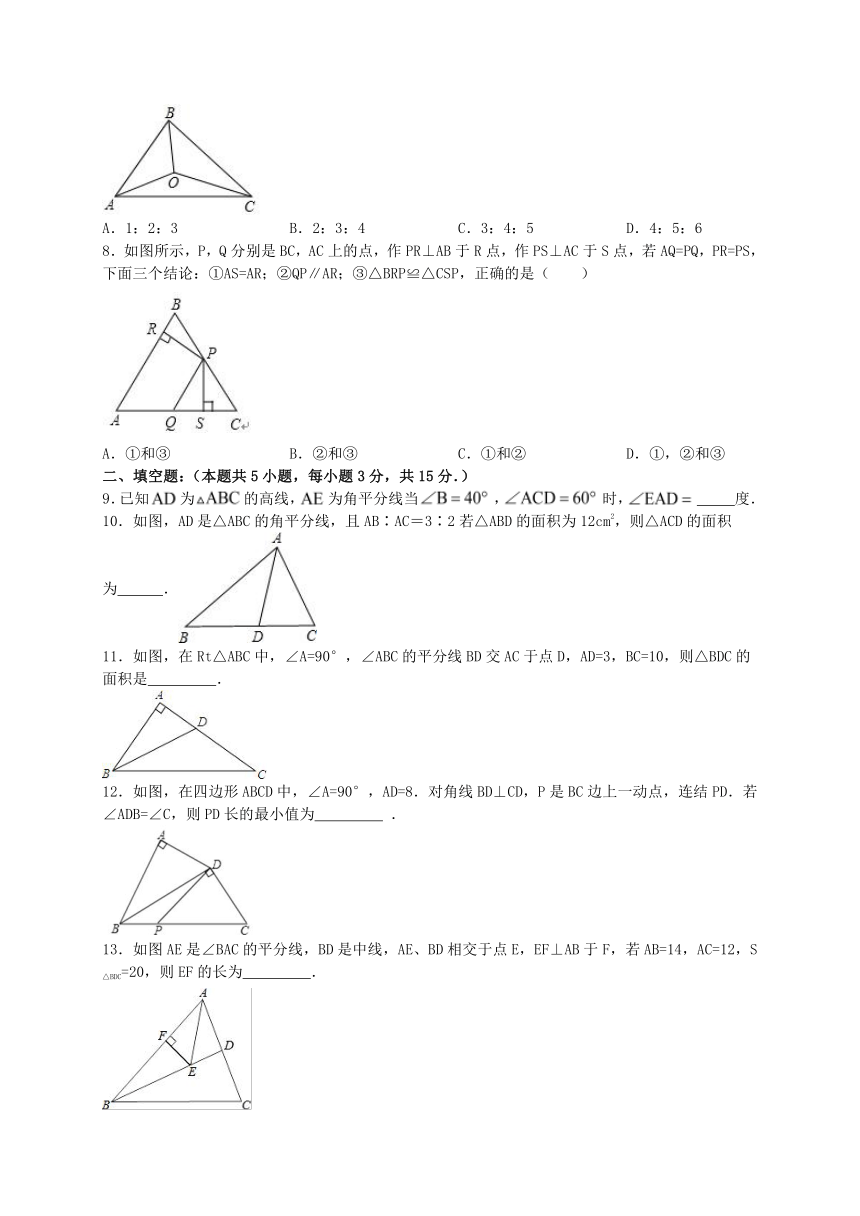
7.如图,△ABC的三边AB,BC,CA的长分别为40、50、60,其三条角平分线交于点O,则S△ABO:S△BCO:S△CAO等于 ( )
A.1:2:3 B.2:3:4 C.3:4:5 D.4:5:6
8.如图所示,P,Q分别是BC,AC上的点,作PR⊥AB于R点,作PS⊥AC于S点,若AQ=PQ,PR=PS,下面三个结论:①AS=AR;②QP∥AR;③△BRP≌△CSP,正确的是( )
A.①和③ B.②和③ C.①和② D.①,②和③
二、填空题:(本题共5小题,每小题3分,共15分.)
9.已知为的高线,为角平分线当,时, 度.
10.如图,AD是△ABC的角平分线,且AB∶AC=3∶2若△ABD的面积为12cm2,则△ACD的面积为 .
11.如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是 .
12.如图,在四边形ABCD中,∠A=90°,AD=8.对角线BD⊥CD,P是BC边上一动点,连结PD.若∠ADB=∠C,则PD长的最小值为 .
13.如图AE是∠BAC的平分线,BD是中线,AE、BD相交于点E,EF⊥AB于F,若AB=14,AC=12,S△BDC=20,则EF的长为 .
三、解答题:(本题共5题,共45分)
14.如图,BE=CF,DE⊥AB的延长线于点E,DF⊥AC于点F,且DB=DC,求证:AD是∠BAC的平分线.
15.如图,已知,平分交的延长线于点E,平分交的延长线于点F,且与交于点G,求证:.
16.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是28cm2,AB=20cm,AC=8cm,求DE的长.
17.如图,四边形ABCD中,CD=CB,AC平分∠DAB,CH⊥AB于点H.
(1)求证:∠ADC+∠B=180°;
(2)若AD=3,AB=8,求AH的长.
18.如图,△ABC中,点D在BC边上,∠BAD=100°,∠ABC的平分线交AC于点E,过点E作EF⊥AB,垂足为F,且∠AEF=50°,连接DE.
(1)求∠CAD的度数;
(2)求证:DE平分∠ADC;
(3)若AB=7,AD=4,CD=8,且S△ACD=15,求△ABE的面积.
参考答案:
1.D 2.A 3.A 4.A 5.A 6.D 7.D 8.C
9.10
10.8cm2
11.15
12.8
13.2
14.证明:∵DE⊥AB的延长线于点E,DF⊥AC于点F,
∴∠BED=∠CFD,
∴△BDE与△CDF是直角三角形,
∵,
∴Rt△BDE≌Rt△CDF,
∴DE=DF,
∴AD是∠BAC的平分线.
15.证明:∵,
∴,
∵平分,平分,
∴,,
∴,
∴,
∴,
∵,
∴.
16.解:∵在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,
∵△ABC面积是28cm2,AB=20cm,AC=8cm,
∴S△ABC= AB DE+ AC DF=28,
即 ×20×DE+ ×8×DF=28,
解得DE=2cm
17.(1)证明:如图,过点作,交的延长线于,
平分,,,
,,
在和中,
,
,
,
,
;
(2)解:,
,
,,
,
又,,
,
,
.
18.(1)解:∵EF⊥AB,且∠AEF=50°,
∴ ,
∵∠BAD=100°,
∴ ;
(2)证明:过点E作EG⊥AD于G,EH⊥BC于H,
∵ ,EF⊥AB,EG⊥AD,
∴EF= EG;
∵BE是∠ABC的平分线,EF⊥AB,EH⊥BC,
∴EF= EH;
∴EG= EH,
∵EG⊥AD,EH⊥BC,
∴DE平分∠ADC;
(3)解:∵ ,
∵EG= EH,AD=4,CD=8,
∴EG= EH= ,
∴EF= EH= ,
∴
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.用尺规作角平分线的依据是( )
A.SAS B.ASA C.AAS D.SSS
2.已知∠AOB=80°,∠BOC=30°,OM平分∠ AOB, ON平分∠AOC则∠MON的度数为( )
A.15° B.15°或55° C.30°或110° D.30°或55°
3.在△ABC中,∠ABC与∠ACB的平分线相交于O,则∠BOC一定( )
A.大于90° B.等于90°
C.小于90° D.小于或等于90°
4.如图△BAC中,∠C=90°,AD是角平分线,DE⊥AB于E,且BC=5cm,BD=3cm,则DE等于( )
A.2cm B.3cm C.4cm D.5cm
5.如图,OP平分∠AOB,PC⊥OA于C,点D是OB上的动点,若PC=6cm,则PD的长可以是( )
A.7cm B.4cm C.5cm D.3cm
6.如图,AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE、CF相交于点D,则①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.以上结论正确的是( )
A.① B.② C.①② D.①②③
7.如图,△ABC的三边AB,BC,CA的长分别为40、50、60,其三条角平分线交于点O,则S△ABO:S△BCO:S△CAO等于 ( )
A.1:2:3 B.2:3:4 C.3:4:5 D.4:5:6
8.如图所示,P,Q分别是BC,AC上的点,作PR⊥AB于R点,作PS⊥AC于S点,若AQ=PQ,PR=PS,下面三个结论:①AS=AR;②QP∥AR;③△BRP≌△CSP,正确的是( )
A.①和③ B.②和③ C.①和② D.①,②和③
二、填空题:(本题共5小题,每小题3分,共15分.)
9.已知为的高线,为角平分线当,时, 度.
10.如图,AD是△ABC的角平分线,且AB∶AC=3∶2若△ABD的面积为12cm2,则△ACD的面积为 .
11.如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是 .
12.如图,在四边形ABCD中,∠A=90°,AD=8.对角线BD⊥CD,P是BC边上一动点,连结PD.若∠ADB=∠C,则PD长的最小值为 .
13.如图AE是∠BAC的平分线,BD是中线,AE、BD相交于点E,EF⊥AB于F,若AB=14,AC=12,S△BDC=20,则EF的长为 .
三、解答题:(本题共5题,共45分)
14.如图,BE=CF,DE⊥AB的延长线于点E,DF⊥AC于点F,且DB=DC,求证:AD是∠BAC的平分线.
15.如图,已知,平分交的延长线于点E,平分交的延长线于点F,且与交于点G,求证:.
16.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是28cm2,AB=20cm,AC=8cm,求DE的长.
17.如图,四边形ABCD中,CD=CB,AC平分∠DAB,CH⊥AB于点H.
(1)求证:∠ADC+∠B=180°;
(2)若AD=3,AB=8,求AH的长.
18.如图,△ABC中,点D在BC边上,∠BAD=100°,∠ABC的平分线交AC于点E,过点E作EF⊥AB,垂足为F,且∠AEF=50°,连接DE.
(1)求∠CAD的度数;
(2)求证:DE平分∠ADC;
(3)若AB=7,AD=4,CD=8,且S△ACD=15,求△ABE的面积.
参考答案:
1.D 2.A 3.A 4.A 5.A 6.D 7.D 8.C
9.10
10.8cm2
11.15
12.8
13.2
14.证明:∵DE⊥AB的延长线于点E,DF⊥AC于点F,
∴∠BED=∠CFD,
∴△BDE与△CDF是直角三角形,
∵,
∴Rt△BDE≌Rt△CDF,
∴DE=DF,
∴AD是∠BAC的平分线.
15.证明:∵,
∴,
∵平分,平分,
∴,,
∴,
∴,
∴,
∵,
∴.
16.解:∵在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,
∵△ABC面积是28cm2,AB=20cm,AC=8cm,
∴S△ABC= AB DE+ AC DF=28,
即 ×20×DE+ ×8×DF=28,
解得DE=2cm
17.(1)证明:如图,过点作,交的延长线于,
平分,,,
,,
在和中,
,
,
,
,
;
(2)解:,
,
,,
,
又,,
,
,
.
18.(1)解:∵EF⊥AB,且∠AEF=50°,
∴ ,
∵∠BAD=100°,
∴ ;
(2)证明:过点E作EG⊥AD于G,EH⊥BC于H,
∵ ,EF⊥AB,EG⊥AD,
∴EF= EG;
∵BE是∠ABC的平分线,EF⊥AB,EH⊥BC,
∴EF= EH;
∴EG= EH,
∵EG⊥AD,EH⊥BC,
∴DE平分∠ADC;
(3)解:∵ ,
∵EG= EH,AD=4,CD=8,
∴EG= EH= ,
∴EF= EH= ,
∴
