经典奥数专题:数与形(试题)数学六年级上册人教版(含答案)
文档属性
| 名称 | 经典奥数专题:数与形(试题)数学六年级上册人教版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-23 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
经典奥数专题:数与形(试题)数学六年级上册人教版
一、选择题
1.用小木棒按下图方式摆放图形,第⑧个图形需要( )根小木棒。
A.33 B.30 C.36 D.27
2.如下图,第5个图形是由( )个小正方形拼成的。
A.16 B.20 C.25 D.36
3.观察下面的点子图,如果按图中的规律画下去,第⑧个方框里应画( )个点。
A.29 B.31 C.33
4.观察下图,请选择最适合的一个填入问号处,能使之呈现出一定的规律性的是( )。
A. B. C. D.
5.古希腊著名的毕达哥拉斯学派把1、3、6、10、15、21…这样的数称为“三角形数”,而把1、4、9、16、25、36…这样的数称为“正方形数”。从下图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻的“三角形数”之和。下列等式中,不符合这一规律的是( )。
A.25=9+16 B.36=15+21 C.49=21+28 D.64=28+36
6.如下图所示,摆1个六边形要用6根小棒,摆2个六边形要用11根小棒,摆3个六边形要用16根小棒……,摆30个六边形要用( )根小棒。
A.151 B.179 C.180
二、填空题
7.观察下图,这样的5张桌子连在一起可以坐( )人,按此规律连下去,坐96人需要( )张桌子。
8.请根据下图中的规律,按要求回答问题。
(1)第5个图形中白色三角形的个数有( )个。
(2)第10个图形中白色三角形的个数有( )个,黑色三角形的个数有( )个。
9.下面图形按一定规律排列,这样第⑥幅图中一共有( )个小正方形。
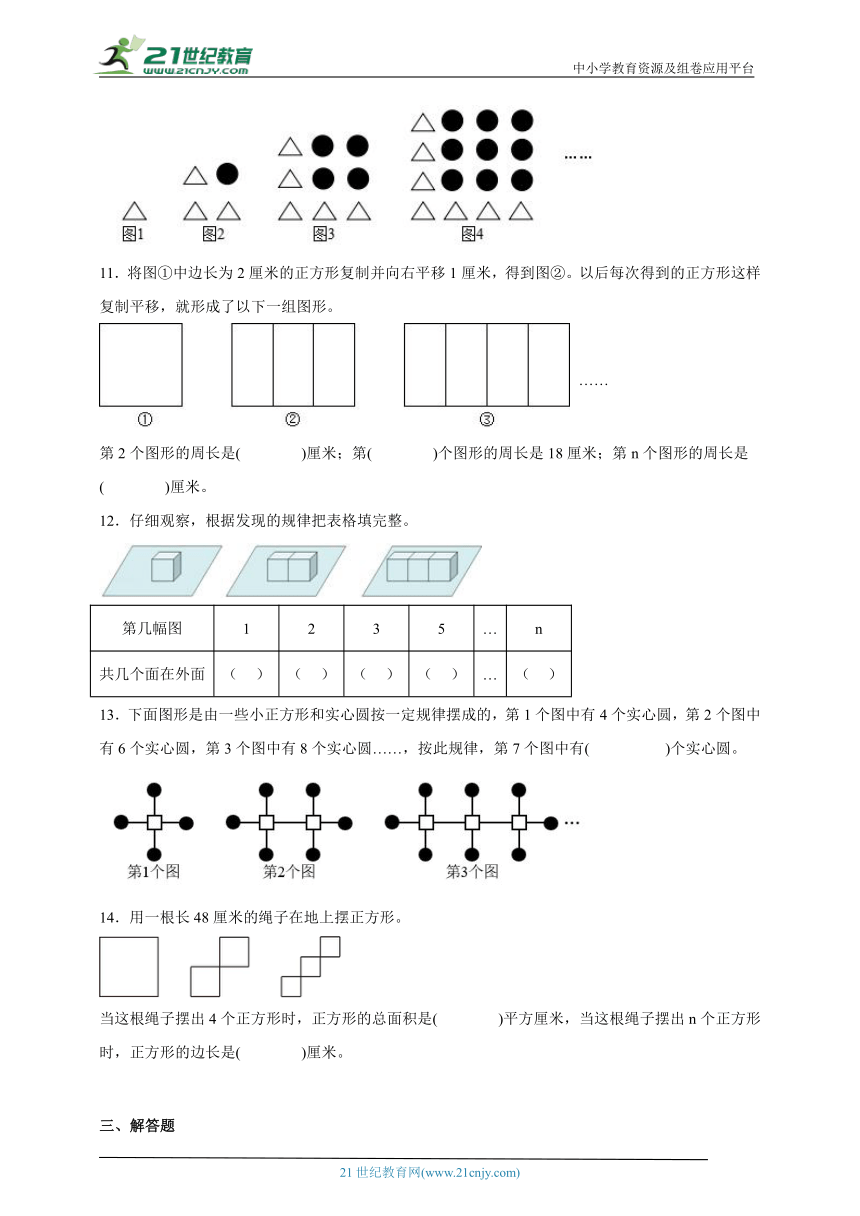
10.根据图中四幅图的规律,第5幅图中有( )个●,第n幅图中有( )个△。
11.将图①中边长为2厘米的正方形复制并向右平移1厘米,得到图②。以后每次得到的正方形这样复制平移,就形成了以下一组图形。
……
第2个图形的周长是( )厘米;第( )个图形的周长是18厘米;第n个图形的周长是( )厘米。
12.仔细观察,根据发现的规律把表格填完整。
第几幅图 1 2 3 5 … n
共几个面在外面 ( ) ( ) ( ) ( ) … ( )
13.下面图形是由一些小正方形和实心圆按一定规律摆成的,第1个图中有4个实心圆,第2个图中有6个实心圆,第3个图中有8个实心圆……,按此规律,第7个图中有( )个实心圆。
14.用一根长48厘米的绳子在地上摆正方形。
当这根绳子摆出4个正方形时,正方形的总面积是( )平方厘米,当这根绳子摆出n个正方形时,正方形的边长是( )厘米。
三、解答题
15.(1)如果下图表示1,请在正方形中用阴影表示。
(2)通过下图,你发现可以怎样非常简便计算的和?写出你的计算方法和结果。
(3)如果在图中继续你的操作,会发现…的和越来越接近于( )。
16.我国苗家的“长桌宴”风俗历史悠久,起源是苗家接亲嫁女、外寨来访贵客的联谊。如果按照这样的方式摆放,接待58人需要准备多少张桌子?
17.下面每个图中各有多少个绿色小正方形和多少个蓝色小正方形?
照这样接着画下去,第6个图形有多少个绿色小正方形和多少个蓝色小正方形?第10个图形呢?你能解释这其中的道理吗?
18.当当在计算“12+1×3×2+32、22+2×5×2+52、42+4×6×2+62 …”这样的算式时,她用“数形结合”的方法来探索:用算式中的数分别构造两个正方形和两个长方形。她发现“这四个图形的面积相加正好是大正方形的面积”(如图所示)。
由此得出:
图①:12+1×3×2+32=42
图②:22+2×5×2+52=72
图③:42+4×6×2+62=102
(1)根据当当发现的规律填空:
32+3×5×2+52=( )。
162+16×19×2+192=( )。
(2)你能根据当当发现的规律,把如图这个正方形分成四块,并用算式表示出来吗?
( )=92
19.下图是由三角形构成的。
(1)填写下表。
图号 ① ② ③ ④
白色三角形个数 ( ) ( ) ( ) ( )
黑色三角形个数 ( ) ( ) ( ) ( )
(2)照这样的规律画下去,第10个图形中有多少个白色三角形、多少个黑色三角形?
20.探索规律。
(1)观察上面的图,发现:
图①空白部分小正方形的个数是22-12=2+1
图②空白部分小正方形的个数是=4+3
图③空白部分小正方形的个数是52-42=( )+( )
(2)像这样继续排列下去,你会发现一些有趣的规律,请你再写出一道算式:( )。
(3)运用规律计算。202-192+182-172+162-152+…+22-12。
参考答案:
1.D
【分析】第1个图形需要6根小木棒,第2个图形需要(6+3)根小木棒,第3个图形需要(6+3×2)根小木棒……每增加一个正方形增加3根小木棒,第n个图形需要[6+3×(n-1)]根小木棒,最后求出n=8时式子的值,据此解答。
【详解】第n个图形需要小木棒的数量:6+3×(n-1)
=6+3n-3×1
=6+3n-3
=3n+6-3
=(3n+3)根
当n=8时。
3n+3
=3×8+3
=24+3
=27(根)
所以,第⑧个图形需要27根小木棒。
故答案为:D
【点睛】本题主要考查数形结合思想的应用,找出小木棒数量的变化规律是解答题目的关键。
2.C
【分析】观察图形,第1个图形是由1×1=1=12个小正方形拼成的,第2个图形是由2×2=4=22个小正方形拼成的,第3个图形是由3×3=9=32个小正方形拼成的,依次类推,可以看出第5个图形是由52个小正方形拼成的。据此解答。
【详解】52=5×5=25(个)
即第5个图形是由25个小正方形拼成的。
故答案为:C
【点睛】此题的解题关键是利用数与形的结合,通过观察图形,把图形中变化的规律转化成数字,多多练习,培养数感。
3.A
【分析】根据图示,第1个方框中的点为:1个;第2个方框中的点为:1+4=5(个);第3个方框中的点为:1+4+4=9(个);第4个方框中的点为:1+4+4+4=12(个);则第n个方框中的点为:1+4(n-1)=(4n-3)个。据此解答。
【详解】第⑧个方框里应画的点数为:
4n-3=4×8-3
=32-3
=29(个)
则第⑧个方框里应画29个点。
故答案为:A
【点睛】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力。
4.C
【分析】观察可知,方框中的圆点数量如,中间4圆点可以呈现出一定的规律性,再根据圆点的呈现方式进行选择。
【详解】如图,具有一定的规律性。
故答案为:C
【点睛】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
5.A
【分析】根据“三角形数”的规律是:1,3,6,10,15,21,28,36,45…,而“正方形数”是两个相邻“三角形数”之和,据此逐项判断即可。
【详解】A.25=9+16;25=52,是正方形数,9和16不是三角形数,不符合规律,符合题意;
B.36=15+21;36=62,是正方形数,15和21是相邻的三角形数,符合规律,不符合题意;
C.49=21+28;49=72,是正方形数,21和28是相邻的三角形数,符合规律,不符合题意;
D.64=28+36;64=82,是正方形数,28和36是相邻的三角形数,符合规律,不符合题意。
故答案为:A
【点睛】解答本题的关键是找清楚“三角形数”和“正方形数”的关系,从而进行求解。
6.A
【分析】摆1个六边形需要1根小棒,摆2个六边形需要根小棒,摆3个六边形需要根小棒,,摆个六边形需要根小棒,据此解答即可。
【详解】摆30个六边形要用:
(根)
所以摆30个六边形要用151根小棒。
故答案为:A
【点睛】本题考查数与形,解答本题的关键是找到题中的规律。
7. 24 23
【分析】把左右两边的4人单独看,则一张桌子对应4个人,一张桌子坐4+1×4=8 (人) , 2张桌子坐4+2×4=12人,3张桌子坐4+3×4=16(人),则n张桌子可以坐(4+4n)人,据此解答即可。
【详解】这样的5张桌子连在一起可以坐的人数为:
4+4n=4+4×5
=4+20
=24
则这样的5张桌子连在一起可以坐24人;
4+4n=96
解:4+4n-4=96-4
4n=92
4n÷4=92÷4
n=23
则坐96人需要23张桌子。
【点睛】本题考查图形的变化规律,发现规律,利用规律是解题的关键。
8.(1)10
(2) 45 55
【分析】观察图形可知:
第1个图形:白色三角形有0个,黑色三角形有1个;
第2个图形:白色三角形有1个,1=0+1;黑色三角形有3个,3=1+2;
第3个图形:白色三角形有3个,3=1+2;黑色三角形有6个,6=1+2+3;
第4个图形:白色三角形有6个,6=1+2+3;黑色三角形有10个,10=1+2+3+4;
……
第n个图形中白色三角形的个数:0+1+2+3+…+(n-1)=n(n-1);
第n个图形中黑色三角形的个数:1+2+3+4+…+n=n(n+1);
据此规律解答。
【详解】(1)规律:第n个图形中白色三角形有n(n-1)个;
当n=5时,白色三角形有:
n(n-1)
=×5×(5-1)
=×5×4
=10(个)
第5个图形中白色三角形的个数有10个。
(2)规律:第n个图形中白色三角形有n(n-1)个,黑色三角形有n(n+1)个;
当n=10时,白色三角形有:
n(n-1)
=×10×(10-1)
=×10×9
=45(个)
当n=10时,黑色三角形有:
n(n+1)
=×10×(10+1)
=×10×11
=55(个)
第10个图形中白色三角形的个数有45个,黑色三角形的个数有55个。
【点睛】通过数与形的结合,从已知的图形或数据中找到规律,并按规律解题。
9.42
【分析】观察图形可知:第①幅图中的小正方形一共有1行,每行2个,第②幅图中的小正方形一共有2行,每行3个,第③幅图中的小正方形一共有3行,每行4个,第④幅图中的小正方形一共有4行,每行5个,据此类推,第n幅图中小正方形一共有n行,每行有(n+1)个, 把n=6代入,算出第⑥幅图中一共有多少小正方形即可。
【详解】由分析可知:
6×(6+1)
=6×7
=42(个)
所以第⑥幅图中一共有42个小正方形。
【点睛】本题重点考查数与形的规律,明确行数和列数之间的关系是解答本题的关键。
10. 16 2n-1
【分析】第一幅图有(1-1)×(1-1)(个)●;第二幅图有(2-1)×(2-1)(个)●;第三幅图有(3-1)×(3-1)(个)●; .....第5幅图有(5-1)×(5-1)(个)●。第一幅图有(2×1-1)(个)O;第二幅图有(2×2-1)(个)O;第三幅图有(2×3-1)(个)O; 第n幅图中的△照此规律即可求。
【详解】第5幅图中●的个数为:(5-1)×(5-1)
=4×4
=16
则第5幅图中有16个●,第n幅图中有(2n-1)个△。
【点睛】仔细观察,比较总结出规律是解决本题的关键。
11. 10 6 2(n+3)
【分析】根据题意,图中每个小长方形的宽是1厘米。第1个图形正方形的周长=2×4=8(厘米),观察图形可以发现,第2个图形的周长比正方形的周长多了2厘米,是2×4+2=2×5=10(厘米);第3个图形的周长比正方形的周长多了4厘米,是2×4+4=2×6=12(厘米)。以此类推,第n个图形的周长=2(n+3)。
图形的周长是18厘米,则2(n+3)=18,根据等式的性质解出方程即可得出图形的序号。
【详解】2×4+2
=8+2
=10(厘米)
则第2个图形的周长是10厘米;
通过分析,第n个图形的周长是2(n+3)厘米;
2(n+3)=18
解:n+3=18÷2
n+3=9
n=6
则第6个图形的周长是18厘米。
【点睛】本题考查数形结合问题。通过观察、计算和分析,发现图形的周长与序号之间的关系是解题的关键。
12.5;9;13;21;1+4n
【分析】每增加1个正方体就增加4个露在外面的面,所以露在外面的面的个数=5+(总个数-1)×4。
【详解】露在外面的面的个数=5+(n-1)×4。
=5+4n-4
=1+4n
第几幅图 1 2 3 5 … n
共几个面在外面 5 9 13 21 … 1+4n
【点睛】掌握图形的变化规律是解题的关键。
13.16
【分析】由图可知:第1个图中有4=2×(1+1)个实心圆,第2个图中有6=2×(2+1)个实心圆;第3个图中有8=2×(3+1)个实心圆……第n个图中有2×(n+1)个实心圆;将n=7代入计算即可。
【详解】第1个图中有4个实心圆,第2个图中有6个实心圆,第3个图中有8个实心圆……,按此规律,第7个图中有2×(7+1)=2×8=16个实心圆。
【点睛】本题主要考查数与形,找出其中的变化规律是解题的关键。
14. 36
【分析】因为是用一根长48厘米的绳子在地上摆正方形,那么在每个图形中,所有正方形的周长之和就是48厘米;正方形的边长等于周长÷4,正方形的面积等于边长×边长;
因为第二个图形中围成两个一样的正方形,所以第二个图形的每个正方形的边长为第一个图形边长的一半,面积也是它的一半;
当围成3个小正方形时,边长为第一个的三分之一,面积也是三分之一。
以此类推:围成n个小正方形时,边长为第一个的n分之一,面积也是n分之一,据此解答即可。
【详解】根据分析可得:
围成一个正方形:
48÷4=12(厘米)
12×12=144(平方厘米)
围成2个正方形:
12÷2=6(厘米)
144÷2=72(平方厘米)
围成3个正方形:
12÷3=4(厘米)
144÷3=48(平方厘米)
围成4个正方形:
12÷4=3(厘米)
144÷4=36(平方厘米)
围成n个小正方形时,边长为第一个的n分之一,也就是12×=(厘米),面积也是n分之一,也就是144×=(平方厘米)。
当这根绳子摆出4个正方形时,正方形的总面积是36平方厘米,当这根绳子摆出n个正方形时,正方形的边长是厘米。
【点睛】本题考查了图形的变化规律,通过观察图形,得出图形的变化与边长及其面积的规律,并能应用规律解决问题。
15.(1)见详解
(2)见详解;
(3)1
【分析】(1)正方形表示“1”,先把正方形平均分成2份,一份是,剩下的也是;然后把剩下的图形平均分成2份,一份是,剩下的也是;再把剩下的图形平均分成2份,一份是,剩下的也是;最后把剩下的图形平均分成2份,一份是,剩下的也是,据此在图中用阴影表示。
(2)计算,通过画图发现最后剩下的是,与算式中最后一个分数相同,那么用整个正方形“1”减去,即是阴影部分,也就是的和,这样计算更简便。
(3)如果在图中继续如上的操作,把剩下的图形平均分成2份,一份是,剩下的也是…,会发现…的和越来越接近于整个正方形,即1。
【详解】(1)如图:
(2)用1减去图形没有涂色部分的分数(与算式中最后一个分数相同),计算更简便。
计算过程如下:
(3)如图:
如果在图中继续你的操作,会发现…的和越来越接近于1。
【点睛】通过画图,发现这组算式的规律,利用规律解答。
16.14张
【分析】根据图示,一张桌子可以坐4×1+2=6(人),两张桌子可以坐4×2+2=10(人)……,n张桌子可以坐(4n+2)人,据此可知桌子的张数等于人数减2的差除以4;据此解答。
【详解】(58-2)÷4
=56÷4
=14(张)
答:接待58人需要准备14张桌子。
【点睛】本题考查了数与形的组合知识,结合找出规律,难度一般。
17.绿色6个;蓝色18个;绿色10个;蓝色26个;见详解
【分析】第1个图形,有1个绿色小正方形,8个蓝色小正方形,8=2×1+6;
第2个图形,有2个绿色小正方形,10个蓝色小正方形,10=2×2+6;
第3个图形,有3个绿色小正方形,12个蓝色小正方形,12=2×3+6;
第4个图形,有4个绿色小正方形,14个蓝色小正方形,14=2×4+6;
……
规律:第n个图形,有n个绿色小正方形,(2n+6)个蓝色小正方形;据此解答。
【详解】规律:第n个图形,有n个绿色小正方形,(2n+6)个蓝色小正方形。
当n=6时,有6个绿色小正方形;
蓝色小正方形有:
2n+6
=2×6+6
=12+6
=18(个)
当n=10时,有10个绿色小正方形;
蓝色小正方形有:
2n+6
=2×10+6
=20+6
=26(个)
答:照这样接着画下去,第6个图形有6个绿色小正方形和18个蓝色小正方形。第10个图形有10个绿色小正方形和26个蓝色小正方形。
道理:从图中发现规律:第n个图形有n个绿色小正方形,(2n+6)个蓝色小正方形。
【点睛】通过数与形的结合,从已知的图形或数据中找到规律,并按规律解题。
18.(1)82,352
(2)22+2×7×2+72
图见详解
【分析】根据题意,用算式中的数分别构造两个正方形和两个长方形。这四个图形的面积相加正好是大正方形的面积,由此可知:
图①:12+1×3×2+32=(1+3)2=42
图②:22+2×5×2+52=(2+5)2=72
图③:42+4×6×2+62=(4+6)2=102
也就是说a2+2ab+b2=(a+b)2,据此规律解答即可。
【详解】(1)根据当当发现的规律填空:
32+3×5×2+52=(3+5)2=82
162+16×19×2+192=(16+19)2=352
(2)你能根据当当发现的规律,把如图这个正方形分成四块,用算式表示出来如下:
22+2×7×2+72=92;
图如下:
【点睛】本题考查了数与形的组合知识,结合题意分析解答即可。
19.(1)见详解(2)45个;55个
【分析】(1)第一个图形,白色三角形数量为0个,黑色三角形数量为1=1个;
第二个图形,白色三角形数量为0+1=1个,黑色三角形数量为1+2=3个;
第三个图形,白色三角形数量为0+1+2=3个,黑色三角形数量为1+2+3=6个;
第四个图形,白色三角形数量为0+1+2+3=6个,黑色三角形数量为1+2+3+4=10个;
……
以此类推:
第n个图形,白色三角形数量为:1+2+……+(n-1)个,黑色三角形数量为:1+2+……+n个,据此解答。
【详解】(1)由分析得:
图号 ① ② ③ ④
白色三角形个数 0 1 3 6
黑色三角形个数 1 3 6 10
(2)白色三角形的个数:
1+2+……+9=45(个)
黑色三角形的个数:
1+2+……+10=55(个)
答:照这样的规律画下去,第10个图形中有45个白色三角形、55个黑色三角形。
【点睛】掌握图形的变化规律是解题的关键。
20.(1)5;4
(2)72-62=7+6
(3)210
【分析】观察算式规律可得:相邻两个数的平方差等于这两个数的和,由此按规律解答即可。
【详解】(1)52-42=5+4
(2)72-62=7+6(答案不唯一)
(3)202-192+182-172+162-152+…+22-12
=20+19+18+17+…+3+2+1
=(20+1)×20÷2
=21×20÷2
=420÷2
=210
【点睛】此题考查数与形结合的规律,进一步培养学生的观察能力和总结能力。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
经典奥数专题:数与形(试题)数学六年级上册人教版
一、选择题
1.用小木棒按下图方式摆放图形,第⑧个图形需要( )根小木棒。
A.33 B.30 C.36 D.27
2.如下图,第5个图形是由( )个小正方形拼成的。
A.16 B.20 C.25 D.36
3.观察下面的点子图,如果按图中的规律画下去,第⑧个方框里应画( )个点。
A.29 B.31 C.33
4.观察下图,请选择最适合的一个填入问号处,能使之呈现出一定的规律性的是( )。
A. B. C. D.
5.古希腊著名的毕达哥拉斯学派把1、3、6、10、15、21…这样的数称为“三角形数”,而把1、4、9、16、25、36…这样的数称为“正方形数”。从下图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻的“三角形数”之和。下列等式中,不符合这一规律的是( )。
A.25=9+16 B.36=15+21 C.49=21+28 D.64=28+36
6.如下图所示,摆1个六边形要用6根小棒,摆2个六边形要用11根小棒,摆3个六边形要用16根小棒……,摆30个六边形要用( )根小棒。
A.151 B.179 C.180
二、填空题
7.观察下图,这样的5张桌子连在一起可以坐( )人,按此规律连下去,坐96人需要( )张桌子。
8.请根据下图中的规律,按要求回答问题。
(1)第5个图形中白色三角形的个数有( )个。
(2)第10个图形中白色三角形的个数有( )个,黑色三角形的个数有( )个。
9.下面图形按一定规律排列,这样第⑥幅图中一共有( )个小正方形。
10.根据图中四幅图的规律,第5幅图中有( )个●,第n幅图中有( )个△。
11.将图①中边长为2厘米的正方形复制并向右平移1厘米,得到图②。以后每次得到的正方形这样复制平移,就形成了以下一组图形。
……
第2个图形的周长是( )厘米;第( )个图形的周长是18厘米;第n个图形的周长是( )厘米。
12.仔细观察,根据发现的规律把表格填完整。
第几幅图 1 2 3 5 … n
共几个面在外面 ( ) ( ) ( ) ( ) … ( )
13.下面图形是由一些小正方形和实心圆按一定规律摆成的,第1个图中有4个实心圆,第2个图中有6个实心圆,第3个图中有8个实心圆……,按此规律,第7个图中有( )个实心圆。
14.用一根长48厘米的绳子在地上摆正方形。
当这根绳子摆出4个正方形时,正方形的总面积是( )平方厘米,当这根绳子摆出n个正方形时,正方形的边长是( )厘米。
三、解答题
15.(1)如果下图表示1,请在正方形中用阴影表示。
(2)通过下图,你发现可以怎样非常简便计算的和?写出你的计算方法和结果。
(3)如果在图中继续你的操作,会发现…的和越来越接近于( )。
16.我国苗家的“长桌宴”风俗历史悠久,起源是苗家接亲嫁女、外寨来访贵客的联谊。如果按照这样的方式摆放,接待58人需要准备多少张桌子?
17.下面每个图中各有多少个绿色小正方形和多少个蓝色小正方形?
照这样接着画下去,第6个图形有多少个绿色小正方形和多少个蓝色小正方形?第10个图形呢?你能解释这其中的道理吗?
18.当当在计算“12+1×3×2+32、22+2×5×2+52、42+4×6×2+62 …”这样的算式时,她用“数形结合”的方法来探索:用算式中的数分别构造两个正方形和两个长方形。她发现“这四个图形的面积相加正好是大正方形的面积”(如图所示)。
由此得出:
图①:12+1×3×2+32=42
图②:22+2×5×2+52=72
图③:42+4×6×2+62=102
(1)根据当当发现的规律填空:
32+3×5×2+52=( )。
162+16×19×2+192=( )。
(2)你能根据当当发现的规律,把如图这个正方形分成四块,并用算式表示出来吗?
( )=92
19.下图是由三角形构成的。
(1)填写下表。
图号 ① ② ③ ④
白色三角形个数 ( ) ( ) ( ) ( )
黑色三角形个数 ( ) ( ) ( ) ( )
(2)照这样的规律画下去,第10个图形中有多少个白色三角形、多少个黑色三角形?
20.探索规律。
(1)观察上面的图,发现:
图①空白部分小正方形的个数是22-12=2+1
图②空白部分小正方形的个数是=4+3
图③空白部分小正方形的个数是52-42=( )+( )
(2)像这样继续排列下去,你会发现一些有趣的规律,请你再写出一道算式:( )。
(3)运用规律计算。202-192+182-172+162-152+…+22-12。
参考答案:
1.D
【分析】第1个图形需要6根小木棒,第2个图形需要(6+3)根小木棒,第3个图形需要(6+3×2)根小木棒……每增加一个正方形增加3根小木棒,第n个图形需要[6+3×(n-1)]根小木棒,最后求出n=8时式子的值,据此解答。
【详解】第n个图形需要小木棒的数量:6+3×(n-1)
=6+3n-3×1
=6+3n-3
=3n+6-3
=(3n+3)根
当n=8时。
3n+3
=3×8+3
=24+3
=27(根)
所以,第⑧个图形需要27根小木棒。
故答案为:D
【点睛】本题主要考查数形结合思想的应用,找出小木棒数量的变化规律是解答题目的关键。
2.C
【分析】观察图形,第1个图形是由1×1=1=12个小正方形拼成的,第2个图形是由2×2=4=22个小正方形拼成的,第3个图形是由3×3=9=32个小正方形拼成的,依次类推,可以看出第5个图形是由52个小正方形拼成的。据此解答。
【详解】52=5×5=25(个)
即第5个图形是由25个小正方形拼成的。
故答案为:C
【点睛】此题的解题关键是利用数与形的结合,通过观察图形,把图形中变化的规律转化成数字,多多练习,培养数感。
3.A
【分析】根据图示,第1个方框中的点为:1个;第2个方框中的点为:1+4=5(个);第3个方框中的点为:1+4+4=9(个);第4个方框中的点为:1+4+4+4=12(个);则第n个方框中的点为:1+4(n-1)=(4n-3)个。据此解答。
【详解】第⑧个方框里应画的点数为:
4n-3=4×8-3
=32-3
=29(个)
则第⑧个方框里应画29个点。
故答案为:A
【点睛】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力。
4.C
【分析】观察可知,方框中的圆点数量如,中间4圆点可以呈现出一定的规律性,再根据圆点的呈现方式进行选择。
【详解】如图,具有一定的规律性。
故答案为:C
【点睛】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
5.A
【分析】根据“三角形数”的规律是:1,3,6,10,15,21,28,36,45…,而“正方形数”是两个相邻“三角形数”之和,据此逐项判断即可。
【详解】A.25=9+16;25=52,是正方形数,9和16不是三角形数,不符合规律,符合题意;
B.36=15+21;36=62,是正方形数,15和21是相邻的三角形数,符合规律,不符合题意;
C.49=21+28;49=72,是正方形数,21和28是相邻的三角形数,符合规律,不符合题意;
D.64=28+36;64=82,是正方形数,28和36是相邻的三角形数,符合规律,不符合题意。
故答案为:A
【点睛】解答本题的关键是找清楚“三角形数”和“正方形数”的关系,从而进行求解。
6.A
【分析】摆1个六边形需要1根小棒,摆2个六边形需要根小棒,摆3个六边形需要根小棒,,摆个六边形需要根小棒,据此解答即可。
【详解】摆30个六边形要用:
(根)
所以摆30个六边形要用151根小棒。
故答案为:A
【点睛】本题考查数与形,解答本题的关键是找到题中的规律。
7. 24 23
【分析】把左右两边的4人单独看,则一张桌子对应4个人,一张桌子坐4+1×4=8 (人) , 2张桌子坐4+2×4=12人,3张桌子坐4+3×4=16(人),则n张桌子可以坐(4+4n)人,据此解答即可。
【详解】这样的5张桌子连在一起可以坐的人数为:
4+4n=4+4×5
=4+20
=24
则这样的5张桌子连在一起可以坐24人;
4+4n=96
解:4+4n-4=96-4
4n=92
4n÷4=92÷4
n=23
则坐96人需要23张桌子。
【点睛】本题考查图形的变化规律,发现规律,利用规律是解题的关键。
8.(1)10
(2) 45 55
【分析】观察图形可知:
第1个图形:白色三角形有0个,黑色三角形有1个;
第2个图形:白色三角形有1个,1=0+1;黑色三角形有3个,3=1+2;
第3个图形:白色三角形有3个,3=1+2;黑色三角形有6个,6=1+2+3;
第4个图形:白色三角形有6个,6=1+2+3;黑色三角形有10个,10=1+2+3+4;
……
第n个图形中白色三角形的个数:0+1+2+3+…+(n-1)=n(n-1);
第n个图形中黑色三角形的个数:1+2+3+4+…+n=n(n+1);
据此规律解答。
【详解】(1)规律:第n个图形中白色三角形有n(n-1)个;
当n=5时,白色三角形有:
n(n-1)
=×5×(5-1)
=×5×4
=10(个)
第5个图形中白色三角形的个数有10个。
(2)规律:第n个图形中白色三角形有n(n-1)个,黑色三角形有n(n+1)个;
当n=10时,白色三角形有:
n(n-1)
=×10×(10-1)
=×10×9
=45(个)
当n=10时,黑色三角形有:
n(n+1)
=×10×(10+1)
=×10×11
=55(个)
第10个图形中白色三角形的个数有45个,黑色三角形的个数有55个。
【点睛】通过数与形的结合,从已知的图形或数据中找到规律,并按规律解题。
9.42
【分析】观察图形可知:第①幅图中的小正方形一共有1行,每行2个,第②幅图中的小正方形一共有2行,每行3个,第③幅图中的小正方形一共有3行,每行4个,第④幅图中的小正方形一共有4行,每行5个,据此类推,第n幅图中小正方形一共有n行,每行有(n+1)个, 把n=6代入,算出第⑥幅图中一共有多少小正方形即可。
【详解】由分析可知:
6×(6+1)
=6×7
=42(个)
所以第⑥幅图中一共有42个小正方形。
【点睛】本题重点考查数与形的规律,明确行数和列数之间的关系是解答本题的关键。
10. 16 2n-1
【分析】第一幅图有(1-1)×(1-1)(个)●;第二幅图有(2-1)×(2-1)(个)●;第三幅图有(3-1)×(3-1)(个)●; .....第5幅图有(5-1)×(5-1)(个)●。第一幅图有(2×1-1)(个)O;第二幅图有(2×2-1)(个)O;第三幅图有(2×3-1)(个)O; 第n幅图中的△照此规律即可求。
【详解】第5幅图中●的个数为:(5-1)×(5-1)
=4×4
=16
则第5幅图中有16个●,第n幅图中有(2n-1)个△。
【点睛】仔细观察,比较总结出规律是解决本题的关键。
11. 10 6 2(n+3)
【分析】根据题意,图中每个小长方形的宽是1厘米。第1个图形正方形的周长=2×4=8(厘米),观察图形可以发现,第2个图形的周长比正方形的周长多了2厘米,是2×4+2=2×5=10(厘米);第3个图形的周长比正方形的周长多了4厘米,是2×4+4=2×6=12(厘米)。以此类推,第n个图形的周长=2(n+3)。
图形的周长是18厘米,则2(n+3)=18,根据等式的性质解出方程即可得出图形的序号。
【详解】2×4+2
=8+2
=10(厘米)
则第2个图形的周长是10厘米;
通过分析,第n个图形的周长是2(n+3)厘米;
2(n+3)=18
解:n+3=18÷2
n+3=9
n=6
则第6个图形的周长是18厘米。
【点睛】本题考查数形结合问题。通过观察、计算和分析,发现图形的周长与序号之间的关系是解题的关键。
12.5;9;13;21;1+4n
【分析】每增加1个正方体就增加4个露在外面的面,所以露在外面的面的个数=5+(总个数-1)×4。
【详解】露在外面的面的个数=5+(n-1)×4。
=5+4n-4
=1+4n
第几幅图 1 2 3 5 … n
共几个面在外面 5 9 13 21 … 1+4n
【点睛】掌握图形的变化规律是解题的关键。
13.16
【分析】由图可知:第1个图中有4=2×(1+1)个实心圆,第2个图中有6=2×(2+1)个实心圆;第3个图中有8=2×(3+1)个实心圆……第n个图中有2×(n+1)个实心圆;将n=7代入计算即可。
【详解】第1个图中有4个实心圆,第2个图中有6个实心圆,第3个图中有8个实心圆……,按此规律,第7个图中有2×(7+1)=2×8=16个实心圆。
【点睛】本题主要考查数与形,找出其中的变化规律是解题的关键。
14. 36
【分析】因为是用一根长48厘米的绳子在地上摆正方形,那么在每个图形中,所有正方形的周长之和就是48厘米;正方形的边长等于周长÷4,正方形的面积等于边长×边长;
因为第二个图形中围成两个一样的正方形,所以第二个图形的每个正方形的边长为第一个图形边长的一半,面积也是它的一半;
当围成3个小正方形时,边长为第一个的三分之一,面积也是三分之一。
以此类推:围成n个小正方形时,边长为第一个的n分之一,面积也是n分之一,据此解答即可。
【详解】根据分析可得:
围成一个正方形:
48÷4=12(厘米)
12×12=144(平方厘米)
围成2个正方形:
12÷2=6(厘米)
144÷2=72(平方厘米)
围成3个正方形:
12÷3=4(厘米)
144÷3=48(平方厘米)
围成4个正方形:
12÷4=3(厘米)
144÷4=36(平方厘米)
围成n个小正方形时,边长为第一个的n分之一,也就是12×=(厘米),面积也是n分之一,也就是144×=(平方厘米)。
当这根绳子摆出4个正方形时,正方形的总面积是36平方厘米,当这根绳子摆出n个正方形时,正方形的边长是厘米。
【点睛】本题考查了图形的变化规律,通过观察图形,得出图形的变化与边长及其面积的规律,并能应用规律解决问题。
15.(1)见详解
(2)见详解;
(3)1
【分析】(1)正方形表示“1”,先把正方形平均分成2份,一份是,剩下的也是;然后把剩下的图形平均分成2份,一份是,剩下的也是;再把剩下的图形平均分成2份,一份是,剩下的也是;最后把剩下的图形平均分成2份,一份是,剩下的也是,据此在图中用阴影表示。
(2)计算,通过画图发现最后剩下的是,与算式中最后一个分数相同,那么用整个正方形“1”减去,即是阴影部分,也就是的和,这样计算更简便。
(3)如果在图中继续如上的操作,把剩下的图形平均分成2份,一份是,剩下的也是…,会发现…的和越来越接近于整个正方形,即1。
【详解】(1)如图:
(2)用1减去图形没有涂色部分的分数(与算式中最后一个分数相同),计算更简便。
计算过程如下:
(3)如图:
如果在图中继续你的操作,会发现…的和越来越接近于1。
【点睛】通过画图,发现这组算式的规律,利用规律解答。
16.14张
【分析】根据图示,一张桌子可以坐4×1+2=6(人),两张桌子可以坐4×2+2=10(人)……,n张桌子可以坐(4n+2)人,据此可知桌子的张数等于人数减2的差除以4;据此解答。
【详解】(58-2)÷4
=56÷4
=14(张)
答:接待58人需要准备14张桌子。
【点睛】本题考查了数与形的组合知识,结合找出规律,难度一般。
17.绿色6个;蓝色18个;绿色10个;蓝色26个;见详解
【分析】第1个图形,有1个绿色小正方形,8个蓝色小正方形,8=2×1+6;
第2个图形,有2个绿色小正方形,10个蓝色小正方形,10=2×2+6;
第3个图形,有3个绿色小正方形,12个蓝色小正方形,12=2×3+6;
第4个图形,有4个绿色小正方形,14个蓝色小正方形,14=2×4+6;
……
规律:第n个图形,有n个绿色小正方形,(2n+6)个蓝色小正方形;据此解答。
【详解】规律:第n个图形,有n个绿色小正方形,(2n+6)个蓝色小正方形。
当n=6时,有6个绿色小正方形;
蓝色小正方形有:
2n+6
=2×6+6
=12+6
=18(个)
当n=10时,有10个绿色小正方形;
蓝色小正方形有:
2n+6
=2×10+6
=20+6
=26(个)
答:照这样接着画下去,第6个图形有6个绿色小正方形和18个蓝色小正方形。第10个图形有10个绿色小正方形和26个蓝色小正方形。
道理:从图中发现规律:第n个图形有n个绿色小正方形,(2n+6)个蓝色小正方形。
【点睛】通过数与形的结合,从已知的图形或数据中找到规律,并按规律解题。
18.(1)82,352
(2)22+2×7×2+72
图见详解
【分析】根据题意,用算式中的数分别构造两个正方形和两个长方形。这四个图形的面积相加正好是大正方形的面积,由此可知:
图①:12+1×3×2+32=(1+3)2=42
图②:22+2×5×2+52=(2+5)2=72
图③:42+4×6×2+62=(4+6)2=102
也就是说a2+2ab+b2=(a+b)2,据此规律解答即可。
【详解】(1)根据当当发现的规律填空:
32+3×5×2+52=(3+5)2=82
162+16×19×2+192=(16+19)2=352
(2)你能根据当当发现的规律,把如图这个正方形分成四块,用算式表示出来如下:
22+2×7×2+72=92;
图如下:
【点睛】本题考查了数与形的组合知识,结合题意分析解答即可。
19.(1)见详解(2)45个;55个
【分析】(1)第一个图形,白色三角形数量为0个,黑色三角形数量为1=1个;
第二个图形,白色三角形数量为0+1=1个,黑色三角形数量为1+2=3个;
第三个图形,白色三角形数量为0+1+2=3个,黑色三角形数量为1+2+3=6个;
第四个图形,白色三角形数量为0+1+2+3=6个,黑色三角形数量为1+2+3+4=10个;
……
以此类推:
第n个图形,白色三角形数量为:1+2+……+(n-1)个,黑色三角形数量为:1+2+……+n个,据此解答。
【详解】(1)由分析得:
图号 ① ② ③ ④
白色三角形个数 0 1 3 6
黑色三角形个数 1 3 6 10
(2)白色三角形的个数:
1+2+……+9=45(个)
黑色三角形的个数:
1+2+……+10=55(个)
答:照这样的规律画下去,第10个图形中有45个白色三角形、55个黑色三角形。
【点睛】掌握图形的变化规律是解题的关键。
20.(1)5;4
(2)72-62=7+6
(3)210
【分析】观察算式规律可得:相邻两个数的平方差等于这两个数的和,由此按规律解答即可。
【详解】(1)52-42=5+4
(2)72-62=7+6(答案不唯一)
(3)202-192+182-172+162-152+…+22-12
=20+19+18+17+…+3+2+1
=(20+1)×20÷2
=21×20÷2
=420÷2
=210
【点睛】此题考查数与形结合的规律,进一步培养学生的观察能力和总结能力。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
