思维拓展:圆(单元练习)数学六年级上册人教版(含答案)
文档属性
| 名称 | 思维拓展:圆(单元练习)数学六年级上册人教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-23 19:28:14 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
思维拓展:圆(单元练习)数学六年级上册人教版
一、选择题
1.一只挂钟的分针长20cm,分针的尖端所走一周的路程是( )。
A.20cm B.20×2=40cm C.20×3.14=62.8cm D.20×2×3.14=125.6cm
2.一个圆环形跑道,内外道相差1米,小明从内道,小刚从外道,各跑一圈,小明比小刚少跑约( )米。
A.3.14 B.6.28 C.1 D.2
3.一个圆形广场的半径是150米,在它的边缘每隔3米栽一棵树,一共可以栽( )棵树。
A.313 B.314 C.315 D.316
4.把一张圆形纸片连续对折三次,并量得曲线的长是1.57cm(如图),那么圆形纸片的直径是( )cm。
A.2 B.4 C.6 D.8
5.要从一张方形纸片中剪下一个面积是12.56平方厘米的圆,这张正方形纸片的面积至少是( )平方厘米(取3.14).
A.24 B.20 C.18 D.16
6.如图,有一个直径是6厘米的圆在一个宽是6厘米的长方形方框(厚度不计)内平移。这个圆不能覆盖部分的面积是( )平方厘米。
A.7.74 B.15.48 C.28.26 D.36
二、填空题
7.一个羊圈依墙而建,呈半圆形,半径是5m,修这个羊圈需要( )米长的栅栏。
8.左图中有( )条对称轴;如果圆的半径是4cm,那么每个圆的周长是( )cm,长方形的面积是( )cm2。
9.学校操场地面上画了一个周长是的圆,六(1)班全体同学站在圆上做游戏,老师站在圆内,他和每个同学之间的距离都相等。老师和每个同学之间的距离是( )。
10.在一个边长是4分米的正方形内剪下一个最大的圆,这个圆的面积是( )平方分米。
11.下图圆的面积是25.12平方厘米,阴影部分的面积是( )平方厘米.
12.如图,把一个圆平均分成若干份,再拼成一个近似的长方形。这个长方形的长与宽的比是( ); 如果这个长方形的长是9.42厘米,那么这个圆的面积是( )平方厘米。
13.一个圆环内圆的半径是4cm,比外圆的半径少1cm,圆环的面积是( )cm2。
14.一个直角三角形,三边长度分别是3厘米、4厘米、5厘米,这个三角形的面积是( )平方厘米;大小两个圆,它们的直径之比是3∶2,那么,周长之比是( ),面积之比是( )。
三、解答题
15.给一把圆形的扇子镶边,共用去62.8cm长的布条(接头忽略不计)。这把扇子的面积约是多少平方厘米?
16.一辆自行车的车轮外直径是0.6米,小明在骑这辆自行车时,能使车轮每分钟转120圈。照这样计算,小明5分钟可以骑行多少米?
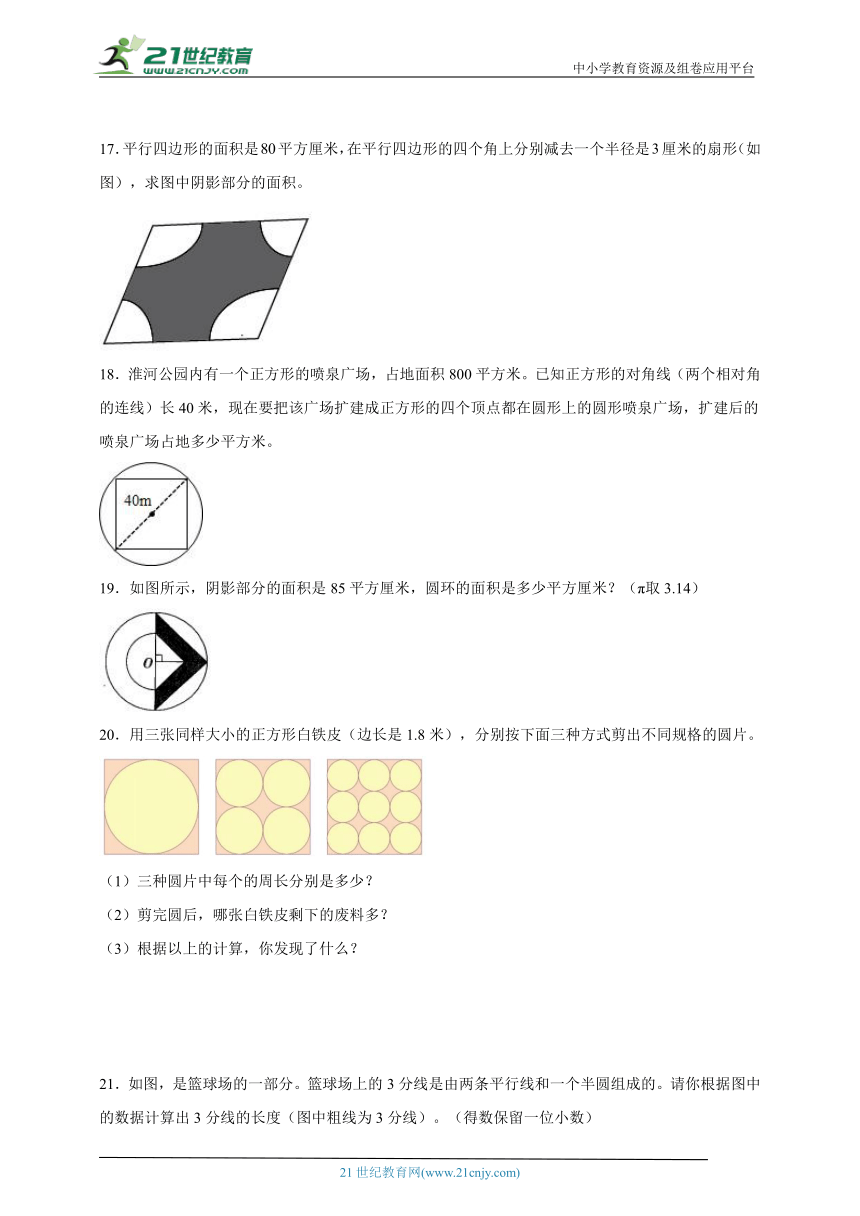
17.平行四边形的面积是平方厘米,在平行四边形的四个角上分别减去一个半径是厘米的扇形(如图),求图中阴影部分的面积。
18.淮河公园内有一个正方形的喷泉广场,占地面积800平方米。已知正方形的对角线(两个相对角的连线)长40米,现在要把该广场扩建成正方形的四个顶点都在圆形上的圆形喷泉广场,扩建后的喷泉广场占地多少平方米。
19.如图所示,阴影部分的面积是85平方厘米,圆环的面积是多少平方厘米?(π取3.14)
20.用三张同样大小的正方形白铁皮(边长是1.8米),分别按下面三种方式剪出不同规格的圆片。
(1)三种圆片中每个的周长分别是多少?
(2)剪完圆后,哪张白铁皮剩下的废料多?
(3)根据以上的计算,你发现了什么?
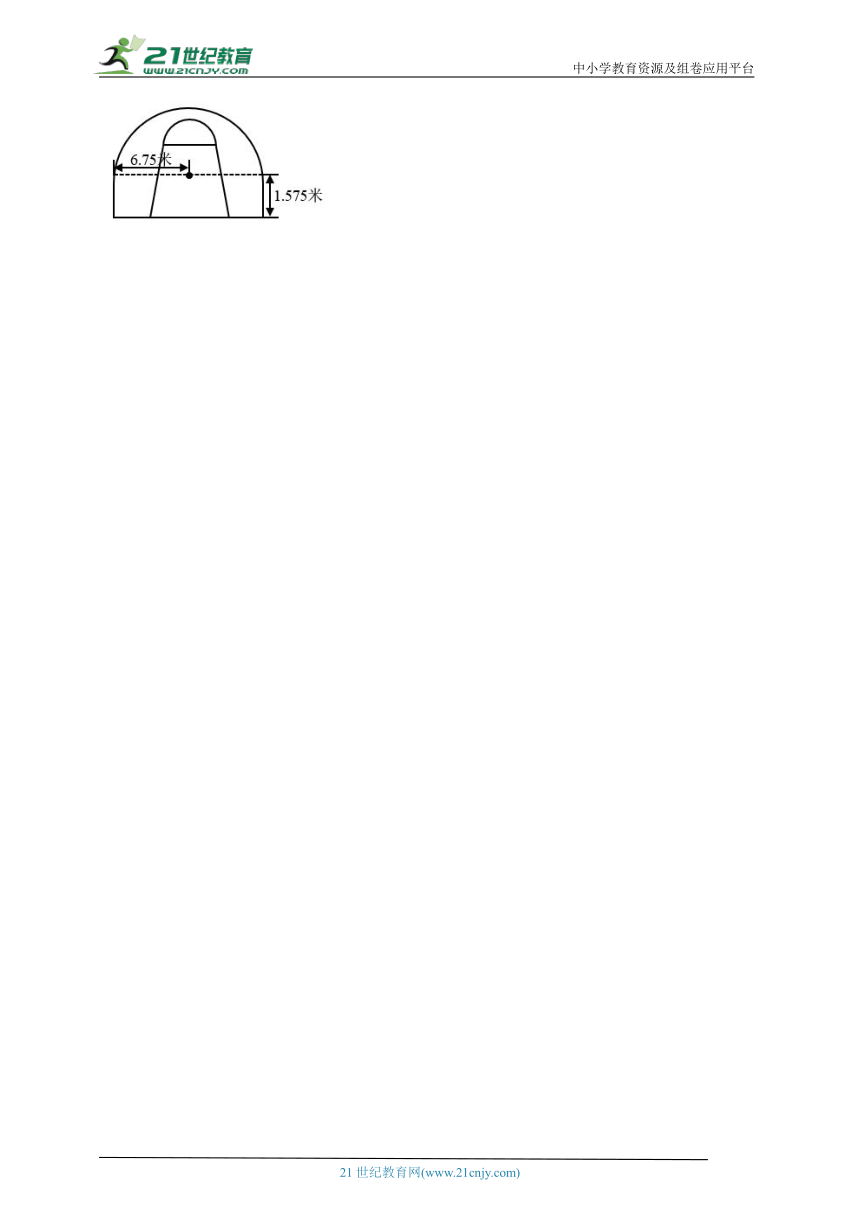
21.如图,是篮球场的一部分。篮球场上的3分线是由两条平行线和一个半圆组成的。请你根据图中的数据计算出3分线的长度(图中粗线为3分线)。(得数保留一位小数)
参考答案:
1.D
【分析】分针针尖所走过的路程就是以分针长为半径的圆的周长。
【详解】3.14×20×2
=62.8×2
=125.6(cm)
所以,分针的尖端所走一周的路程是125.6cm。
故答案为:D
【点睛】此题主要是考查圆周长计算知识,解题关键是熟记圆的周长公式。
2.B
【分析】内外道相差1米,即外圆和内圆的半径之差为1米,利用圆的周长公式C=2πr即可求解。
【详解】2πR-2πr
=2π(R-r)
=2×3.14×1
=6.28(米)
故答案为:B
【点睛】此题主要考查圆的周长公式的灵活应用。
3.B
【分析】先根据圆的周长公式C=2πr,求出圆形广场一周的长度;再根据封闭图形的植树问题:棵数=间隔数,用圆形广场的周长除以间距即可求出一共栽树的棵数。
【详解】2×3.14×150
=6.28×150
=942(米)
942÷3=314(棵)
故答案为:B
【点睛】本题考查封闭图形的植树问题:棵数=间隔数;掌握圆的周长公式是解题的关键。
4.B
【分析】把一张圆形纸片连续对折三次,平均分成了2×2×2份,据此确定曲线占周长的几分之几,设圆形纸片的直径是xcm,根据πd×曲线对应分率=1.57cm,列出方程求出x的值即可。
【详解】2×2×2=8(份)
解:设圆形纸片的直径是xcm。
3.14×x×=1.57
0.3925x=1.57
0.3925x÷0.3925=1.57÷0.3925
x=4
圆形纸片的直径是4cm。
故答案为:B
【点睛】关键是掌握并灵活运用圆的周长公式,用方程解决问题的关键是找到等量关系。
5.D
【详解】设圆的半径为r,则正方形纸张的边长为2r,
则r2=12.56÷3.14,
=4;
正方形的面积:
2r×2r,
=4r2,
=4×4,
=16(平方厘米);
故选D.
【点睛】需要的正方形纸张的边长应等于圆的直径,圆的面积已知,于是可以利用圆的面积求出半径的平方值,而正方形的边长等于2×半径,从而可以求出正方形纸张的面积.
6.A
【分析】如图所示,这个圆不能覆盖的面积是1、2、3、4四部分的面积,把3和4向左平移至3’和4’的位置,这个圆不能覆盖部分的面积=正方形的面积-圆的面积,据此解答。
【详解】6×6-3.14×(6÷2)2
=6×6-3.14×9
=36-28.26
=7.74(平方厘米)
所以,这个圆不能覆盖部分的面积是7.74平方厘米。
故答案为:A
【点睛】准确找出这个圆不能覆盖部分的面积,并把该面积转化为正方形的面积和圆的面积的差是解答题目的关键。
7.15.7
【分析】根据题意可知,就是求圆周长的一半,用“C=2πr”求出圆的周长,再除以2即可。
【详解】2×3.14×5÷2
=31.4÷2
=15.7(米)
【点睛】熟练掌握圆的周长公式是解答本题的关键。
8. 2 25.12 128
【分析】一个图形沿一条直线对折后,折痕两旁的部分能够完全重合,这样的图形就是轴对称图形,这条直线就是对称轴。
已知圆的半径是4cm,根据圆的周长公式C=2πr,即可求出每个圆的周长。
观察图形可知,长方形的长等于半径的4倍,宽等于半径的2倍,由此求出长方形的长与宽;再根据长方形的面积=长×宽,求出这个长方形的面积。
【详解】如图,有2条对称轴。
圆的周长:2×3.14×4=25.12(cm)
长方形的面积:
(4×4)×(4×2)
=16×8
=128(cm2)
图中有2条对称轴,每个圆的周长是25.12cm,长方形的面积是128cm2。
【点睛】本题考查根据轴对称图形的意义及特点、圆的周长公式的运用、长方形面积公式的运用。
9.5
【分析】老师站在圆内,他和每个同学之间的距离都相等,说明老师在圆心处,师和每个同学之间的距离就是周长为31.4m的半径,据此解答即可。
【详解】31.4÷3.14÷2
=10÷2
=5(m)
【点睛】本题考查圆的周长,解答本题的关键是掌握圆的周长公式。
10.12.56
【分析】这个圆的直径就是正方形的边长,先计算出圆的半径(直径÷2),再依据圆的面积公式(S=πr2)即可求其面积。
【详解】圆的面积:
3.14×(4÷2)2
=3.14×4
=12.56(平方分米)
【点睛】此题主要考查正方形及圆的面积公式,关键是明白圆的直径即为正方形的边长。
11.8
【详解】略
12. π∶1 28.26
【分析】由圆的面积推导过程可知:将圆拼成近似的长方形后,长方形的长就等于圆的周长的一半,宽就等于圆的半径,根据圆周长公式:C=2πr,可知圆的周长的一半表示为πr,据此写出这个长方形的长与宽的比,再化简即可;如果这个长方形的长是9.42厘米,则圆的周长是(9.42×2)厘米,根据圆周长公式:C=2πr,用周长÷2÷3.14即可求出圆的半径;最后根据圆面积公式:S=πr2,代入数据解答即可。
【详解】这个长方形的长与宽的比:
πr∶r
=(πr÷r)∶(r÷r)
=π∶1
半径:9.42×2÷2÷3.14=3(厘米)
3.14×32
=3.14×9
=28.26(平方厘米)
把一个圆平均分成若干份,再拼成一个近似的长方形。这个长方形的长与宽的比是π∶1; 如果这个长方形的长是9.42厘米,那么这个圆的面积是28.26平方厘米。
【点睛】本题主要考查了圆周长公式、圆面积公式的灵活应用以及比的化简,解答此题的主要依据是圆的面积推导过程。
13.28.26
【分析】先用圆环的内圆半径加1cm求出外圆的半径;再根据圆环的面积求出圆环的面积。
【详解】4+1=5(cm)
3.14×(52-42)
=3.14×(25-16)
=3.14×9
=28.26(cm2)
所以圆环的面积是28.26 cm2。
【点睛】求圆环面积时要先算出的是两圆半径的“平方差”,而不是“差的平方”。
14. 6 3∶2 9∶4
【分析】直角三角形中斜边最长,两条直角边互为彼此的底和高,利用“”求出这个三角形的面积;假设出两个圆的直径,利用“”“”分别表示出这两个圆的周长和面积,最后求出它们的周长比和面积比,据此解答。
【详解】3×4÷2
=12÷2
=6(平方厘米)
所以,这个三角形的面积是6平方厘米。
假设大圆的直径为厘米,小圆的直径为厘米。
大圆的周长:=(厘米)
小圆的周长:=(厘米)
大圆的周长∶小圆的周长
=∶
=3∶2
大圆的面积:
=
=
=(平方厘米)
小圆的面积:
=
=(平方厘米)
大圆的面积∶小圆的面积
=∶
=∶1
=(×4)∶(1×4)
=9∶4
所以,周长之比是3∶2,面积之比是9∶4。
【点睛】掌握三角形的面积以及圆的周长和面积的计算公式是解答题目的关键。
15.314平方厘米
【分析】根据圆的周长公式,先求出扇面的半径,再根据圆的面积=πr ,列式解答。
【详解】62.8÷3.14÷2=10(厘米)
3.14×10 =314(平方厘米)
答:这把扇子的面积约是314平方厘米。
【点睛】关键是掌握圆的周长和面积公式,圆的周长=πd=2πr。
16.1130.4米
【分析】根据圆周长公式,用0.6×3.14即可求出车轮每圈走的长度,然后根据乘法的意义,用0.6×3.14×120即可求出车轮每分钟走的长度,再用车轮每分钟走的长度×5即可求出小明5分钟可以骑行多少米。
【详解】0.6×3.14×120×5
=1.884×120×5
=226.08×5
=1130.4(米)
答:小明5分钟可以骑行1130.4米。
【点睛】本题考查了圆周长公式的灵活应用。
17.51.74平方厘米
【分析】平行四边形的内角和是360°,四个角的扇形合起来正好是一个圆,图中阴影部分的面积=平行四边形的面积-圆的面积,据此代入数据计算即可。
【详解】80-3.14×32
=80-28.26
=51.74(平方厘米)
答:图中阴影部分的面积是51.74平方厘米。
【点睛】熟练运用圆的面积公式S=πr2是解题的关键。
18.1256平方米
【分析】由图可知,正方形的对角线40米是圆的直径,则圆的半径为20米,利用即可求得扩建后喷泉广场的占地面积。
【详解】3.14×(40÷2)2
=3.14×202
=3.14×400
=1256(平方米)
答:扩建后的喷泉广场占地1256平方米。
【点睛】掌握圆的面积计算公式是解答题目的关键。
19.266.9平方厘米
【分析】设大圆的半径为,小圆的半径为,环形的面积,又因阴影部分的面积平方厘米(大三角形面积减去小三角形面积),从而就可以求出环形的面积。
【详解】解:设大圆的半径为,小圆的半径为,
因为,
则环形的面积:
(平方厘米)
答:环形的面积是266.9平方厘米。
【点睛】解答此题的关键是得出的值,利用等量代换即可求出环形的面积。
20.(1)5.652米;2.826米;1.884米
(2)同样多
(3)见详解
【分析】(1)第一种圆片的直径=正方形边长,第二种圆片的直径=正方形边长÷2,第三种圆片的直径=正方形边长÷3,根据圆的周长=πd,列式解答即可。
(2)剩下的废料面积=正方形面积-所有圆的面积,正方形面积=边长×边长,圆的面积=πr2,据此列式解答。
(3)根据剩下的废料的面积即可得出结论。
【详解】(1)1.8÷2=0.9(米)
1.8÷3=0.6(米)
第一种:3.14×1.8=5.652(米)
第二种:3.14×0.9=2.826(米)
第三种:3.14×0.6=1.884(米)
答:三种圆片中每个的周长分别是5.652米、2.826米、1.884米。
(2)1.8×1.8=3.24(平方米)
3.24-3.14×(1.8÷2)2
=3.24-3.14×0.92
=3.24-3.14×0.81
=3.24-2.5434
=0.6966(平方米)
3.24-3.14×(0.9÷2)2×4
=3.24-3.14×0.452×4
=3.24-3.14×0.2025×4
=3.24-2.5434
=0.6966(平方米)
3.24-3.14×(0.6÷2)2×9
=3.24-3.14×0.32×9
=3.24-3.14×0.09×9
=3.24-2.5434
=0.6966(平方米)
答:剪完圆后,三张白铁皮剩下的废料同样多。
(3)发现:按这三种方式剪完圆后,三张白铁皮剩下的废料同样多,这说明剪掉的圆的面积的和也是相等的。照此推测,按这样的方式剪圆片,无论怎样剪,剩下的废料总是不变的。
【点睛】关键是掌握并灵活运用圆的周长和面积公式。
21.24.3米
【分析】观察图形可知,3分线的长度=圆周长的一半+2条平行线的长度;根据圆的周长公式C=πd,代入数据计算即可。
【详解】
(米)
答:3分线的长度约是24.3米。
【点睛】本题考查圆周长公式的运用,先分析出组合图形的周长是由哪些线段和曲线组成,再根据图形周长公式解答即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
思维拓展:圆(单元练习)数学六年级上册人教版
一、选择题
1.一只挂钟的分针长20cm,分针的尖端所走一周的路程是( )。
A.20cm B.20×2=40cm C.20×3.14=62.8cm D.20×2×3.14=125.6cm
2.一个圆环形跑道,内外道相差1米,小明从内道,小刚从外道,各跑一圈,小明比小刚少跑约( )米。
A.3.14 B.6.28 C.1 D.2
3.一个圆形广场的半径是150米,在它的边缘每隔3米栽一棵树,一共可以栽( )棵树。
A.313 B.314 C.315 D.316
4.把一张圆形纸片连续对折三次,并量得曲线的长是1.57cm(如图),那么圆形纸片的直径是( )cm。
A.2 B.4 C.6 D.8
5.要从一张方形纸片中剪下一个面积是12.56平方厘米的圆,这张正方形纸片的面积至少是( )平方厘米(取3.14).
A.24 B.20 C.18 D.16
6.如图,有一个直径是6厘米的圆在一个宽是6厘米的长方形方框(厚度不计)内平移。这个圆不能覆盖部分的面积是( )平方厘米。
A.7.74 B.15.48 C.28.26 D.36
二、填空题
7.一个羊圈依墙而建,呈半圆形,半径是5m,修这个羊圈需要( )米长的栅栏。
8.左图中有( )条对称轴;如果圆的半径是4cm,那么每个圆的周长是( )cm,长方形的面积是( )cm2。
9.学校操场地面上画了一个周长是的圆,六(1)班全体同学站在圆上做游戏,老师站在圆内,他和每个同学之间的距离都相等。老师和每个同学之间的距离是( )。
10.在一个边长是4分米的正方形内剪下一个最大的圆,这个圆的面积是( )平方分米。
11.下图圆的面积是25.12平方厘米,阴影部分的面积是( )平方厘米.
12.如图,把一个圆平均分成若干份,再拼成一个近似的长方形。这个长方形的长与宽的比是( ); 如果这个长方形的长是9.42厘米,那么这个圆的面积是( )平方厘米。
13.一个圆环内圆的半径是4cm,比外圆的半径少1cm,圆环的面积是( )cm2。
14.一个直角三角形,三边长度分别是3厘米、4厘米、5厘米,这个三角形的面积是( )平方厘米;大小两个圆,它们的直径之比是3∶2,那么,周长之比是( ),面积之比是( )。
三、解答题
15.给一把圆形的扇子镶边,共用去62.8cm长的布条(接头忽略不计)。这把扇子的面积约是多少平方厘米?
16.一辆自行车的车轮外直径是0.6米,小明在骑这辆自行车时,能使车轮每分钟转120圈。照这样计算,小明5分钟可以骑行多少米?
17.平行四边形的面积是平方厘米,在平行四边形的四个角上分别减去一个半径是厘米的扇形(如图),求图中阴影部分的面积。
18.淮河公园内有一个正方形的喷泉广场,占地面积800平方米。已知正方形的对角线(两个相对角的连线)长40米,现在要把该广场扩建成正方形的四个顶点都在圆形上的圆形喷泉广场,扩建后的喷泉广场占地多少平方米。
19.如图所示,阴影部分的面积是85平方厘米,圆环的面积是多少平方厘米?(π取3.14)
20.用三张同样大小的正方形白铁皮(边长是1.8米),分别按下面三种方式剪出不同规格的圆片。
(1)三种圆片中每个的周长分别是多少?
(2)剪完圆后,哪张白铁皮剩下的废料多?
(3)根据以上的计算,你发现了什么?
21.如图,是篮球场的一部分。篮球场上的3分线是由两条平行线和一个半圆组成的。请你根据图中的数据计算出3分线的长度(图中粗线为3分线)。(得数保留一位小数)
参考答案:
1.D
【分析】分针针尖所走过的路程就是以分针长为半径的圆的周长。
【详解】3.14×20×2
=62.8×2
=125.6(cm)
所以,分针的尖端所走一周的路程是125.6cm。
故答案为:D
【点睛】此题主要是考查圆周长计算知识,解题关键是熟记圆的周长公式。
2.B
【分析】内外道相差1米,即外圆和内圆的半径之差为1米,利用圆的周长公式C=2πr即可求解。
【详解】2πR-2πr
=2π(R-r)
=2×3.14×1
=6.28(米)
故答案为:B
【点睛】此题主要考查圆的周长公式的灵活应用。
3.B
【分析】先根据圆的周长公式C=2πr,求出圆形广场一周的长度;再根据封闭图形的植树问题:棵数=间隔数,用圆形广场的周长除以间距即可求出一共栽树的棵数。
【详解】2×3.14×150
=6.28×150
=942(米)
942÷3=314(棵)
故答案为:B
【点睛】本题考查封闭图形的植树问题:棵数=间隔数;掌握圆的周长公式是解题的关键。
4.B
【分析】把一张圆形纸片连续对折三次,平均分成了2×2×2份,据此确定曲线占周长的几分之几,设圆形纸片的直径是xcm,根据πd×曲线对应分率=1.57cm,列出方程求出x的值即可。
【详解】2×2×2=8(份)
解:设圆形纸片的直径是xcm。
3.14×x×=1.57
0.3925x=1.57
0.3925x÷0.3925=1.57÷0.3925
x=4
圆形纸片的直径是4cm。
故答案为:B
【点睛】关键是掌握并灵活运用圆的周长公式,用方程解决问题的关键是找到等量关系。
5.D
【详解】设圆的半径为r,则正方形纸张的边长为2r,
则r2=12.56÷3.14,
=4;
正方形的面积:
2r×2r,
=4r2,
=4×4,
=16(平方厘米);
故选D.
【点睛】需要的正方形纸张的边长应等于圆的直径,圆的面积已知,于是可以利用圆的面积求出半径的平方值,而正方形的边长等于2×半径,从而可以求出正方形纸张的面积.
6.A
【分析】如图所示,这个圆不能覆盖的面积是1、2、3、4四部分的面积,把3和4向左平移至3’和4’的位置,这个圆不能覆盖部分的面积=正方形的面积-圆的面积,据此解答。
【详解】6×6-3.14×(6÷2)2
=6×6-3.14×9
=36-28.26
=7.74(平方厘米)
所以,这个圆不能覆盖部分的面积是7.74平方厘米。
故答案为:A
【点睛】准确找出这个圆不能覆盖部分的面积,并把该面积转化为正方形的面积和圆的面积的差是解答题目的关键。
7.15.7
【分析】根据题意可知,就是求圆周长的一半,用“C=2πr”求出圆的周长,再除以2即可。
【详解】2×3.14×5÷2
=31.4÷2
=15.7(米)
【点睛】熟练掌握圆的周长公式是解答本题的关键。
8. 2 25.12 128
【分析】一个图形沿一条直线对折后,折痕两旁的部分能够完全重合,这样的图形就是轴对称图形,这条直线就是对称轴。
已知圆的半径是4cm,根据圆的周长公式C=2πr,即可求出每个圆的周长。
观察图形可知,长方形的长等于半径的4倍,宽等于半径的2倍,由此求出长方形的长与宽;再根据长方形的面积=长×宽,求出这个长方形的面积。
【详解】如图,有2条对称轴。
圆的周长:2×3.14×4=25.12(cm)
长方形的面积:
(4×4)×(4×2)
=16×8
=128(cm2)
图中有2条对称轴,每个圆的周长是25.12cm,长方形的面积是128cm2。
【点睛】本题考查根据轴对称图形的意义及特点、圆的周长公式的运用、长方形面积公式的运用。
9.5
【分析】老师站在圆内,他和每个同学之间的距离都相等,说明老师在圆心处,师和每个同学之间的距离就是周长为31.4m的半径,据此解答即可。
【详解】31.4÷3.14÷2
=10÷2
=5(m)
【点睛】本题考查圆的周长,解答本题的关键是掌握圆的周长公式。
10.12.56
【分析】这个圆的直径就是正方形的边长,先计算出圆的半径(直径÷2),再依据圆的面积公式(S=πr2)即可求其面积。
【详解】圆的面积:
3.14×(4÷2)2
=3.14×4
=12.56(平方分米)
【点睛】此题主要考查正方形及圆的面积公式,关键是明白圆的直径即为正方形的边长。
11.8
【详解】略
12. π∶1 28.26
【分析】由圆的面积推导过程可知:将圆拼成近似的长方形后,长方形的长就等于圆的周长的一半,宽就等于圆的半径,根据圆周长公式:C=2πr,可知圆的周长的一半表示为πr,据此写出这个长方形的长与宽的比,再化简即可;如果这个长方形的长是9.42厘米,则圆的周长是(9.42×2)厘米,根据圆周长公式:C=2πr,用周长÷2÷3.14即可求出圆的半径;最后根据圆面积公式:S=πr2,代入数据解答即可。
【详解】这个长方形的长与宽的比:
πr∶r
=(πr÷r)∶(r÷r)
=π∶1
半径:9.42×2÷2÷3.14=3(厘米)
3.14×32
=3.14×9
=28.26(平方厘米)
把一个圆平均分成若干份,再拼成一个近似的长方形。这个长方形的长与宽的比是π∶1; 如果这个长方形的长是9.42厘米,那么这个圆的面积是28.26平方厘米。
【点睛】本题主要考查了圆周长公式、圆面积公式的灵活应用以及比的化简,解答此题的主要依据是圆的面积推导过程。
13.28.26
【分析】先用圆环的内圆半径加1cm求出外圆的半径;再根据圆环的面积求出圆环的面积。
【详解】4+1=5(cm)
3.14×(52-42)
=3.14×(25-16)
=3.14×9
=28.26(cm2)
所以圆环的面积是28.26 cm2。
【点睛】求圆环面积时要先算出的是两圆半径的“平方差”,而不是“差的平方”。
14. 6 3∶2 9∶4
【分析】直角三角形中斜边最长,两条直角边互为彼此的底和高,利用“”求出这个三角形的面积;假设出两个圆的直径,利用“”“”分别表示出这两个圆的周长和面积,最后求出它们的周长比和面积比,据此解答。
【详解】3×4÷2
=12÷2
=6(平方厘米)
所以,这个三角形的面积是6平方厘米。
假设大圆的直径为厘米,小圆的直径为厘米。
大圆的周长:=(厘米)
小圆的周长:=(厘米)
大圆的周长∶小圆的周长
=∶
=3∶2
大圆的面积:
=
=
=(平方厘米)
小圆的面积:
=
=(平方厘米)
大圆的面积∶小圆的面积
=∶
=∶1
=(×4)∶(1×4)
=9∶4
所以,周长之比是3∶2,面积之比是9∶4。
【点睛】掌握三角形的面积以及圆的周长和面积的计算公式是解答题目的关键。
15.314平方厘米
【分析】根据圆的周长公式,先求出扇面的半径,再根据圆的面积=πr ,列式解答。
【详解】62.8÷3.14÷2=10(厘米)
3.14×10 =314(平方厘米)
答:这把扇子的面积约是314平方厘米。
【点睛】关键是掌握圆的周长和面积公式,圆的周长=πd=2πr。
16.1130.4米
【分析】根据圆周长公式,用0.6×3.14即可求出车轮每圈走的长度,然后根据乘法的意义,用0.6×3.14×120即可求出车轮每分钟走的长度,再用车轮每分钟走的长度×5即可求出小明5分钟可以骑行多少米。
【详解】0.6×3.14×120×5
=1.884×120×5
=226.08×5
=1130.4(米)
答:小明5分钟可以骑行1130.4米。
【点睛】本题考查了圆周长公式的灵活应用。
17.51.74平方厘米
【分析】平行四边形的内角和是360°,四个角的扇形合起来正好是一个圆,图中阴影部分的面积=平行四边形的面积-圆的面积,据此代入数据计算即可。
【详解】80-3.14×32
=80-28.26
=51.74(平方厘米)
答:图中阴影部分的面积是51.74平方厘米。
【点睛】熟练运用圆的面积公式S=πr2是解题的关键。
18.1256平方米
【分析】由图可知,正方形的对角线40米是圆的直径,则圆的半径为20米,利用即可求得扩建后喷泉广场的占地面积。
【详解】3.14×(40÷2)2
=3.14×202
=3.14×400
=1256(平方米)
答:扩建后的喷泉广场占地1256平方米。
【点睛】掌握圆的面积计算公式是解答题目的关键。
19.266.9平方厘米
【分析】设大圆的半径为,小圆的半径为,环形的面积,又因阴影部分的面积平方厘米(大三角形面积减去小三角形面积),从而就可以求出环形的面积。
【详解】解:设大圆的半径为,小圆的半径为,
因为,
则环形的面积:
(平方厘米)
答:环形的面积是266.9平方厘米。
【点睛】解答此题的关键是得出的值,利用等量代换即可求出环形的面积。
20.(1)5.652米;2.826米;1.884米
(2)同样多
(3)见详解
【分析】(1)第一种圆片的直径=正方形边长,第二种圆片的直径=正方形边长÷2,第三种圆片的直径=正方形边长÷3,根据圆的周长=πd,列式解答即可。
(2)剩下的废料面积=正方形面积-所有圆的面积,正方形面积=边长×边长,圆的面积=πr2,据此列式解答。
(3)根据剩下的废料的面积即可得出结论。
【详解】(1)1.8÷2=0.9(米)
1.8÷3=0.6(米)
第一种:3.14×1.8=5.652(米)
第二种:3.14×0.9=2.826(米)
第三种:3.14×0.6=1.884(米)
答:三种圆片中每个的周长分别是5.652米、2.826米、1.884米。
(2)1.8×1.8=3.24(平方米)
3.24-3.14×(1.8÷2)2
=3.24-3.14×0.92
=3.24-3.14×0.81
=3.24-2.5434
=0.6966(平方米)
3.24-3.14×(0.9÷2)2×4
=3.24-3.14×0.452×4
=3.24-3.14×0.2025×4
=3.24-2.5434
=0.6966(平方米)
3.24-3.14×(0.6÷2)2×9
=3.24-3.14×0.32×9
=3.24-3.14×0.09×9
=3.24-2.5434
=0.6966(平方米)
答:剪完圆后,三张白铁皮剩下的废料同样多。
(3)发现:按这三种方式剪完圆后,三张白铁皮剩下的废料同样多,这说明剪掉的圆的面积的和也是相等的。照此推测,按这样的方式剪圆片,无论怎样剪,剩下的废料总是不变的。
【点睛】关键是掌握并灵活运用圆的周长和面积公式。
21.24.3米
【分析】观察图形可知,3分线的长度=圆周长的一半+2条平行线的长度;根据圆的周长公式C=πd,代入数据计算即可。
【详解】
(米)
答:3分线的长度约是24.3米。
【点睛】本题考查圆周长公式的运用,先分析出组合图形的周长是由哪些线段和曲线组成,再根据图形周长公式解答即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
