24.2.1点和圆的位置关系 课件(共35张PPT)
文档属性
| 名称 | 24.2.1点和圆的位置关系 课件(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 21.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-22 21:41:31 | ||
图片预览







文档简介
(共35张PPT)
24.2.1 点和圆的位置关系
人教版九年级上册
知识回顾
1.圆的大小由 确定;位置由 确定.
2.线段垂直平分线上的点到线段两个 的距离 .
3.到线段两端点的距离相等的点在线段的 上.
半径
圆心
端点
相等
垂直平分线
教学目标
1.理解并掌握点和圆的三种位置关系.
2.经历探索点与圆的三种位置关系,体会数学分类讨论思考问题的方法.
新知导入
2016年里约奥运会, 首次参加奥运会的张梦雪在女子10米气手枪决赛夺得金牌,以199.4环的总成绩创造决赛奥运会纪录,这也是中国体育代表团在里约奥运会的首枚金牌。
新知导入
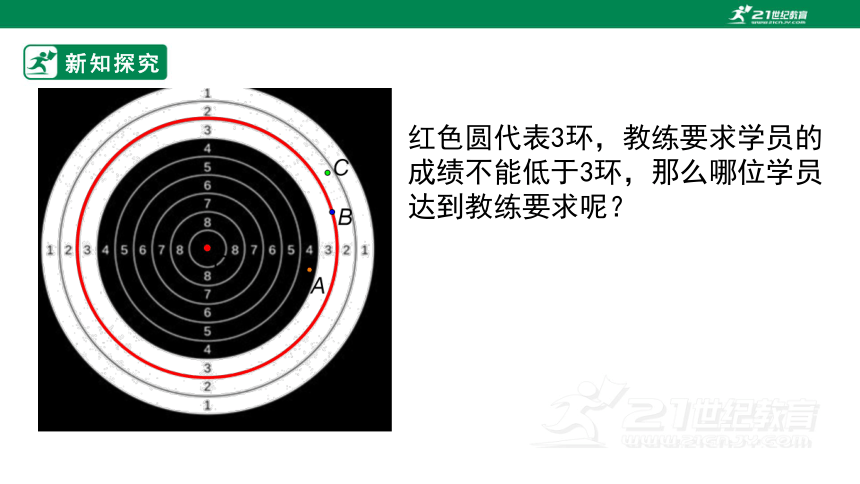
射击靶图是由许多圆心相同,半径不等的同心圆构成,圆心就是靶心,射击成绩由射击弹着点与靶心之间的距离决定,弹着点距离靶心越近,对应的环数越高,成绩也越好。
新知探究
点A、点B、点C分别是A、B、C三位射击学员的射击弹着点,那么哪位学员的成绩最好呢?原因是什么呢?
点A距离靶心最近,因此学员A的成绩最好。
新知探究
红色圆代表3环,教练要求学员的成绩不能低于3环,那么哪位学员达到教练要求呢?
新知探究
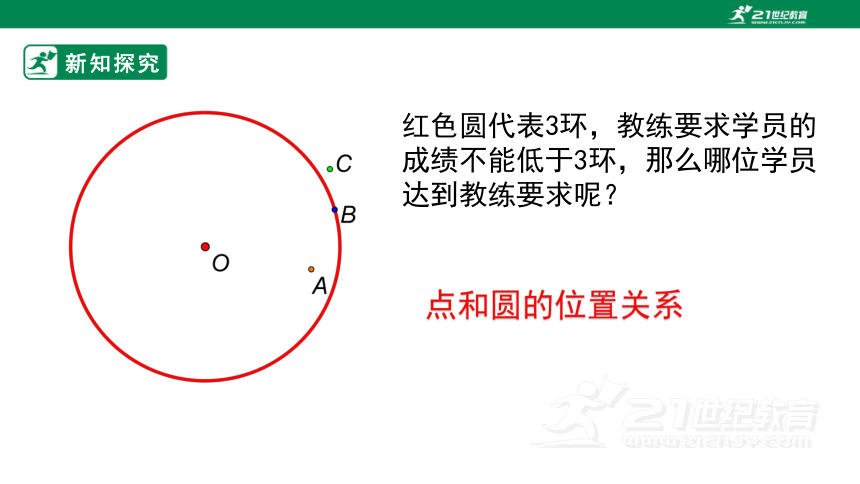
红色圆代表3环,教练要求学员的成绩不能低于3环,那么哪位学员达到教练要求呢?
点和圆的位置关系
新知探究
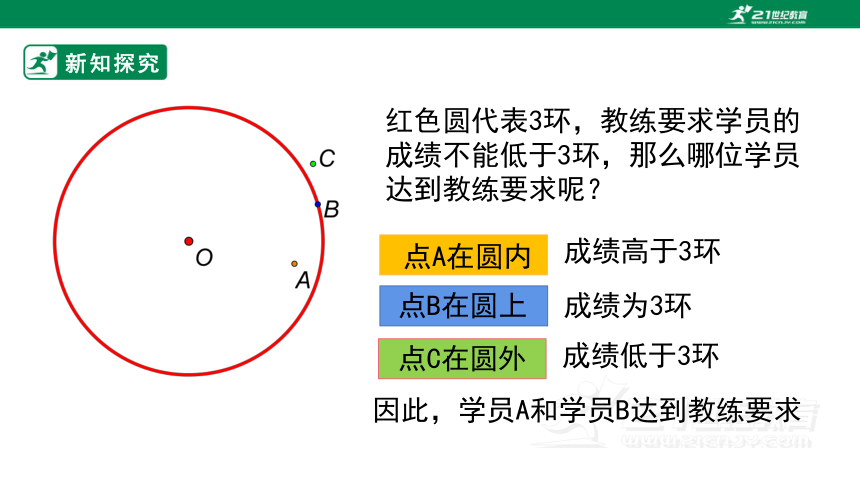
红色圆代表3环,教练要求学员的成绩不能低于3环,那么哪位学员达到教练要求呢?
点B在圆上
点A在圆内
点C在圆外
成绩为3环
成绩高于3环
成绩低于3环
因此,学员A和学员B达到教练要求
新知探究
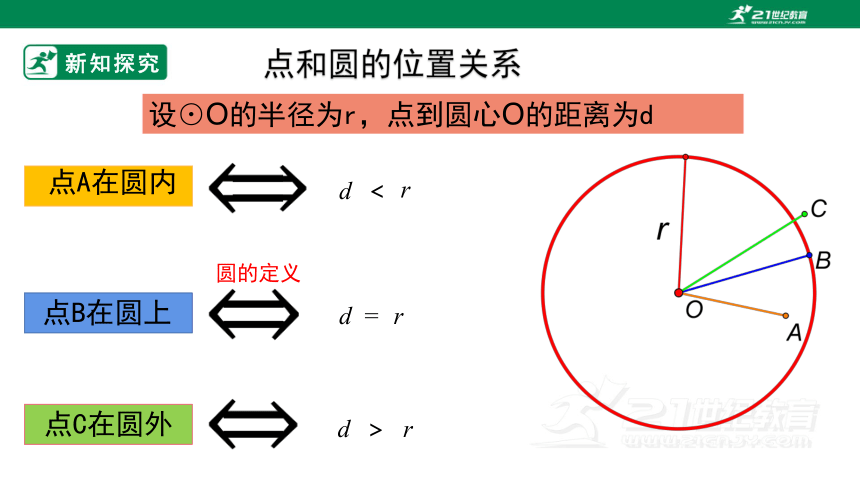
点和圆的位置关系
点B在圆上
点A在圆内
点C在圆外
设⊙O的半径为r,点到圆心O的距离为d
圆的定义
d
d
d
<
r
r
=
>
r
新知探究
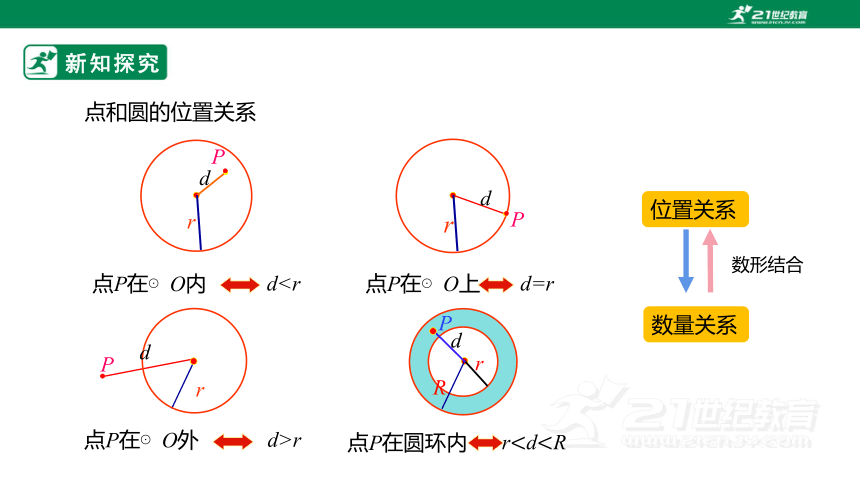
点和圆的位置关系
r
P
d
P
r
d
P
r
d
点P在⊙O内
d点P在⊙O上
d=r
点P在圆环内
r数形结合
位置关系
数量关系
R
r
P
d
点P在⊙O外
d>r
新知小结
1.判断点与圆的位置关系的实质是判断点到圆心的距离和半径的大小关系.
2.已知点到圆心的距离与半径的数量关系,可以确定该点与圆的位置关系,反过来,由点与圆的位置关系也可以确定该点到圆心的距离与半径的数量关系.
3.圆的外部可以看成到圆心的距离大于半径的点的集合;圆的内部可以看成到圆心的距离小于半径的点的集合.
新知探究
思考:(1)我们知道圆心和半径可以确定一个圆,如果只知道圆上的点,能不能确定圆呢?
如何过一个点A作一个圆?过点A可以作多少个圆?
解:任取一点为圆心,以圆心到点A的距离为半径,画圆,可作无数个圆.
·
·
·
·
·
A
新知探究
(2)如何过两点A、B作一个圆?过两点可以作多少个圆?
·
·
·
·
A
B
解:作线段AB的垂直平分线,以其上任意一点为圆心,以这点到点A或点B的距离为半径画圆即.
可作无数个圆.
新知探究
(3)过不在同一直线上的三点能不能确定一个圆?
A
B
C
D
E
G
F
●o
经过B,C两点的圆的圆心在线段BC的垂直平分线上.
经过A,B,C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.
经过A,B两点的圆的圆心在线段AB的垂直平分线上.
不在同一直线上的三个点确定一个圆
新知探究
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
锐角三角形的外接圆圆心位于三角形内
直角三角形的外心位于直角三角形斜边的中点
钝角三角形的外心位于三角形外
新知小结
1.经过已知点A可以作 个圆,经过两个已知点A,B可以作 个圆,它们的圆心在线段AB的 上;经过不在同一条直线上的A,B,C三点可以作 个圆.
无数
无数
垂直平分线
一
新知小结
2.经过三角形的 的圆叫做三角形的外接圆,外接圆的圆心是三角形三条边的 的交点,叫做这个三角形的外心.
性质:到三角形三个顶点的距离相等.
三个顶点
垂直平分线
●O
A
B
C
任意三角形的外接圆有______个,而一个圆的内接三角形有______个.
一
无数
新知探究
经过同一条直线上的三个点能作出一个圆吗?
经过不在同一条直线上的三点A,B,C可作一个圆
l1
l2
A
B
C
P
如图,假设过同一条直线l上三点A,B,C可以作一个圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点,而l1⊥l,l2⊥l 这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾,所以过同一条直线上的三点不能作圆.
l
新知小结
反证法的定义
先假设命题的结论不成立,然后由此经过推理得出矛盾(常与公理、定理、定义或已知条件相矛盾),由矛盾判定假设不正确,从而得到原命题成立,这种方法叫做反证法.
反证法的一般步骤
假设命题的结论不成立
②从这个假设出发,经过推理,得出矛盾
③由矛盾判定假设不正确,从而肯定命题的结论正确
新知典例
如图,在△ABC中,∠ACB=90°,AC=12,AB=13,CD⊥AB于点D,以点C为圆心,5为半径作⊙C,试判断A,D,B三点与⊙C的位置关系.
例1
解:在Rt△ABC中,由勾股定理,得
∴点B在⊙C上.
∵S△ABC= AC·BC= AB·CD,
∴CD= <5,
∴点D在⊙C内.
又∵AC=12>5,∴点A在⊙C外.
新知练习
1.⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8 cm、10 cm、12 cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 .
圆O内
圆O上
圆O外
新知典例
如图所示的是残缺的破圆形轮片,如何找此残片所在的圆的圆心.(不写作法,保留作图痕迹)
例2
A
B
C
O
解:方法:
1.在圆弧上任取三点A、B、C;
2.作线段AB、BC的垂直平分线,其交点O即为圆心;
3.以点O为圆心,OC长为半径作圆.
⊙O即为所求.
总结:在弧上任意找两条弦,分别作它们的垂直平分线,两条垂直平分线的交点即是圆心.
新知练习
2.如图,在平面直角坐标系中,一圆弧过正方形网格的格点A,B,C,已知点A的坐标是( -3,5) ,则该圆弧所在圆的圆心P的坐标是 .
(-1,0)
解:圆弧所在圆的圆心是AB与BC的垂直平分线的交点.
AB 的垂直平分线是 x=-1,
点B的坐标是(1,5),C 的坐标是(4,2),
BC 的垂直平分线与 x=-1的交点的纵坐标是0,
因而该圆弧所在圆的圆心坐标是(-1,0).
新知探究
用反证法证明:若∠A,∠B,∠C是△ABC的三个内角,则其中至少有一个角不大于60°.
例3
证明:假设∠A,∠B,∠C都大于60°.
则有∠A+∠B+∠C >180°,
这与三角形的内角和等于180°相矛盾.
因此假设不成立,
即∠A,∠B,∠C中至少有一个角不大于60°.
新知练习
如图,我们要证明:如果AB∥CD,那么∠1=∠2.
假设∠1≠∠2,过点O作直线A′B′,
使∠EOB′=∠2.根据“同位角相等,两直线平行”,
可得A′B′∥CD.
这样,过点O就有两条直线AB,A′B′都平行于CD,
这与平行公理“过直线外一点有且仅有一条直线与已知直线平行”矛盾.
这说明假设∠1≠∠2不正确,从而∠1=∠2.
3.用反证法证明平行线的性质“两直线平行,同位角相等”.
证明:
课堂总结
点与圆的位置关系
点在圆外
点在圆上
点在圆内
d>r
d=r
d位置关系数量化
作圆
过一点可以作无数个圆
过两点可以作无数个圆
定理:过不在同一直线上的三个点确定一个圆
一个三角形的外接圆是唯一的.
点P在圆环内
rR
r
P
反证法的证明思想:反设、归谬、结论
课堂练习
1.在直角坐标系中,⊙A,⊙B的位置如图所示.下列四个点中,在⊙A外部且在⊙B内部的是( )
A.(1,2) B.(2,1)
C.(2,-1) D.(3,1)
2.在平面直角坐标系中,⊙A的半径是4,圆心A的坐标是(2,0),则点P(-2,1)与⊙A的位置关系是 .
C
点P在⊙A外部
课堂练习
3.如图,在⊙O中,∠CBD=30°,∠BDC=20°,求∠A的度数.
解:∵在△BCD中,∠CBD=30°,∠BDC=20°,
∴∠C=180°-∠CBD-∠BDC=130°.
∵四边形ABCD是圆内接四边形,
∴∠A=180°-∠C=50°.
课堂练习
4.如图,△ABC中,∠ACB= 90°,AC=2 cm, BC=4 cm,CM是AB边上的中线.
(1) 若以C为圆心, cm为半径画圆,则点A,B,M与⊙C的位置关系如何
(2) 若以C为圆心作⊙C,使点A,B,M中至少有一点在圆内,且至少有一点在圆外,求⊙C的半径 r 的取值范围.
解:(1) 因为CA=2 cm< cm,所以点A在⊙C内.
因为BC=4 cm> cm,所以点B在⊙C外.
由勾股定理,得AB==2 (cm) ,
所以 CM=AB= cm,所以点M在⊙C上.
课堂练习
解:(2)当点B在圆上时, r=4 cm,
当点A在圆上时,r=2 cm,
当点M在圆上时, r= cm,
故满足题意的 r 的取值范围是2 cm< r <4 cm.
4.如图,△ABC中,∠ACB= 90°,AC=2 cm, BC=4 cm,CM是AB边上的中线.
(1) 若以C为圆心, cm为半径画圆,则点A,B,M与⊙C的位置关系如何
(2) 若以C为圆心作⊙C,使点A,B,M中至少有一点在圆内,且至少有一点在圆外,求⊙C的半径 r 的取值范围.
课堂练习
5.如图,已知矩形ABCD的边AB=3,AD=4.
(1) 以A为圆心,4为半径作⊙A,则点B,C,D与⊙A的位置关系如何?
解:AD=4= r,故D点在⊙A上,
AB=3< r, 故B点在⊙A内,
AC==5> r,故C点在⊙A外.
课堂练习
(2) 若以A点为圆心作⊙A,使B,C,D三点中至少有一点在圆内,且至少有一点在圆外,求⊙A的半径r的取值范围?(直接写出答案)
35.如图,已知矩形ABCD的边AB=3,AD=4.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
24.2.1 点和圆的位置关系
人教版九年级上册
知识回顾
1.圆的大小由 确定;位置由 确定.
2.线段垂直平分线上的点到线段两个 的距离 .
3.到线段两端点的距离相等的点在线段的 上.
半径
圆心
端点
相等
垂直平分线
教学目标
1.理解并掌握点和圆的三种位置关系.
2.经历探索点与圆的三种位置关系,体会数学分类讨论思考问题的方法.
新知导入
2016年里约奥运会, 首次参加奥运会的张梦雪在女子10米气手枪决赛夺得金牌,以199.4环的总成绩创造决赛奥运会纪录,这也是中国体育代表团在里约奥运会的首枚金牌。
新知导入
射击靶图是由许多圆心相同,半径不等的同心圆构成,圆心就是靶心,射击成绩由射击弹着点与靶心之间的距离决定,弹着点距离靶心越近,对应的环数越高,成绩也越好。
新知探究
点A、点B、点C分别是A、B、C三位射击学员的射击弹着点,那么哪位学员的成绩最好呢?原因是什么呢?
点A距离靶心最近,因此学员A的成绩最好。
新知探究
红色圆代表3环,教练要求学员的成绩不能低于3环,那么哪位学员达到教练要求呢?
新知探究
红色圆代表3环,教练要求学员的成绩不能低于3环,那么哪位学员达到教练要求呢?
点和圆的位置关系
新知探究
红色圆代表3环,教练要求学员的成绩不能低于3环,那么哪位学员达到教练要求呢?
点B在圆上
点A在圆内
点C在圆外
成绩为3环
成绩高于3环
成绩低于3环
因此,学员A和学员B达到教练要求
新知探究
点和圆的位置关系
点B在圆上
点A在圆内
点C在圆外
设⊙O的半径为r,点到圆心O的距离为d
圆的定义
d
d
d
<
r
r
=
>
r
新知探究
点和圆的位置关系
r
P
d
P
r
d
P
r
d
点P在⊙O内
d
d=r
点P在圆环内
r
位置关系
数量关系
R
r
P
d
点P在⊙O外
d>r
新知小结
1.判断点与圆的位置关系的实质是判断点到圆心的距离和半径的大小关系.
2.已知点到圆心的距离与半径的数量关系,可以确定该点与圆的位置关系,反过来,由点与圆的位置关系也可以确定该点到圆心的距离与半径的数量关系.
3.圆的外部可以看成到圆心的距离大于半径的点的集合;圆的内部可以看成到圆心的距离小于半径的点的集合.
新知探究
思考:(1)我们知道圆心和半径可以确定一个圆,如果只知道圆上的点,能不能确定圆呢?
如何过一个点A作一个圆?过点A可以作多少个圆?
解:任取一点为圆心,以圆心到点A的距离为半径,画圆,可作无数个圆.
·
·
·
·
·
A
新知探究
(2)如何过两点A、B作一个圆?过两点可以作多少个圆?
·
·
·
·
A
B
解:作线段AB的垂直平分线,以其上任意一点为圆心,以这点到点A或点B的距离为半径画圆即.
可作无数个圆.
新知探究
(3)过不在同一直线上的三点能不能确定一个圆?
A
B
C
D
E
G
F
●o
经过B,C两点的圆的圆心在线段BC的垂直平分线上.
经过A,B,C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.
经过A,B两点的圆的圆心在线段AB的垂直平分线上.
不在同一直线上的三个点确定一个圆
新知探究
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
锐角三角形的外接圆圆心位于三角形内
直角三角形的外心位于直角三角形斜边的中点
钝角三角形的外心位于三角形外
新知小结
1.经过已知点A可以作 个圆,经过两个已知点A,B可以作 个圆,它们的圆心在线段AB的 上;经过不在同一条直线上的A,B,C三点可以作 个圆.
无数
无数
垂直平分线
一
新知小结
2.经过三角形的 的圆叫做三角形的外接圆,外接圆的圆心是三角形三条边的 的交点,叫做这个三角形的外心.
性质:到三角形三个顶点的距离相等.
三个顶点
垂直平分线
●O
A
B
C
任意三角形的外接圆有______个,而一个圆的内接三角形有______个.
一
无数
新知探究
经过同一条直线上的三个点能作出一个圆吗?
经过不在同一条直线上的三点A,B,C可作一个圆
l1
l2
A
B
C
P
如图,假设过同一条直线l上三点A,B,C可以作一个圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点,而l1⊥l,l2⊥l 这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾,所以过同一条直线上的三点不能作圆.
l
新知小结
反证法的定义
先假设命题的结论不成立,然后由此经过推理得出矛盾(常与公理、定理、定义或已知条件相矛盾),由矛盾判定假设不正确,从而得到原命题成立,这种方法叫做反证法.
反证法的一般步骤
假设命题的结论不成立
②从这个假设出发,经过推理,得出矛盾
③由矛盾判定假设不正确,从而肯定命题的结论正确
新知典例
如图,在△ABC中,∠ACB=90°,AC=12,AB=13,CD⊥AB于点D,以点C为圆心,5为半径作⊙C,试判断A,D,B三点与⊙C的位置关系.
例1
解:在Rt△ABC中,由勾股定理,得
∴点B在⊙C上.
∵S△ABC= AC·BC= AB·CD,
∴CD= <5,
∴点D在⊙C内.
又∵AC=12>5,∴点A在⊙C外.
新知练习
1.⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8 cm、10 cm、12 cm,则点A、B、C与⊙O的位置关系是:点A在 ;点B在 ;点C在 .
圆O内
圆O上
圆O外
新知典例
如图所示的是残缺的破圆形轮片,如何找此残片所在的圆的圆心.(不写作法,保留作图痕迹)
例2
A
B
C
O
解:方法:
1.在圆弧上任取三点A、B、C;
2.作线段AB、BC的垂直平分线,其交点O即为圆心;
3.以点O为圆心,OC长为半径作圆.
⊙O即为所求.
总结:在弧上任意找两条弦,分别作它们的垂直平分线,两条垂直平分线的交点即是圆心.
新知练习
2.如图,在平面直角坐标系中,一圆弧过正方形网格的格点A,B,C,已知点A的坐标是( -3,5) ,则该圆弧所在圆的圆心P的坐标是 .
(-1,0)
解:圆弧所在圆的圆心是AB与BC的垂直平分线的交点.
AB 的垂直平分线是 x=-1,
点B的坐标是(1,5),C 的坐标是(4,2),
BC 的垂直平分线与 x=-1的交点的纵坐标是0,
因而该圆弧所在圆的圆心坐标是(-1,0).
新知探究
用反证法证明:若∠A,∠B,∠C是△ABC的三个内角,则其中至少有一个角不大于60°.
例3
证明:假设∠A,∠B,∠C都大于60°.
则有∠A+∠B+∠C >180°,
这与三角形的内角和等于180°相矛盾.
因此假设不成立,
即∠A,∠B,∠C中至少有一个角不大于60°.
新知练习
如图,我们要证明:如果AB∥CD,那么∠1=∠2.
假设∠1≠∠2,过点O作直线A′B′,
使∠EOB′=∠2.根据“同位角相等,两直线平行”,
可得A′B′∥CD.
这样,过点O就有两条直线AB,A′B′都平行于CD,
这与平行公理“过直线外一点有且仅有一条直线与已知直线平行”矛盾.
这说明假设∠1≠∠2不正确,从而∠1=∠2.
3.用反证法证明平行线的性质“两直线平行,同位角相等”.
证明:
课堂总结
点与圆的位置关系
点在圆外
点在圆上
点在圆内
d>r
d=r
d
作圆
过一点可以作无数个圆
过两点可以作无数个圆
定理:过不在同一直线上的三个点确定一个圆
一个三角形的外接圆是唯一的.
点P在圆环内
r
r
P
反证法的证明思想:反设、归谬、结论
课堂练习
1.在直角坐标系中,⊙A,⊙B的位置如图所示.下列四个点中,在⊙A外部且在⊙B内部的是( )
A.(1,2) B.(2,1)
C.(2,-1) D.(3,1)
2.在平面直角坐标系中,⊙A的半径是4,圆心A的坐标是(2,0),则点P(-2,1)与⊙A的位置关系是 .
C
点P在⊙A外部
课堂练习
3.如图,在⊙O中,∠CBD=30°,∠BDC=20°,求∠A的度数.
解:∵在△BCD中,∠CBD=30°,∠BDC=20°,
∴∠C=180°-∠CBD-∠BDC=130°.
∵四边形ABCD是圆内接四边形,
∴∠A=180°-∠C=50°.
课堂练习
4.如图,△ABC中,∠ACB= 90°,AC=2 cm, BC=4 cm,CM是AB边上的中线.
(1) 若以C为圆心, cm为半径画圆,则点A,B,M与⊙C的位置关系如何
(2) 若以C为圆心作⊙C,使点A,B,M中至少有一点在圆内,且至少有一点在圆外,求⊙C的半径 r 的取值范围.
解:(1) 因为CA=2 cm< cm,所以点A在⊙C内.
因为BC=4 cm> cm,所以点B在⊙C外.
由勾股定理,得AB==2 (cm) ,
所以 CM=AB= cm,所以点M在⊙C上.
课堂练习
解:(2)当点B在圆上时, r=4 cm,
当点A在圆上时,r=2 cm,
当点M在圆上时, r= cm,
故满足题意的 r 的取值范围是2 cm< r <4 cm.
4.如图,△ABC中,∠ACB= 90°,AC=2 cm, BC=4 cm,CM是AB边上的中线.
(1) 若以C为圆心, cm为半径画圆,则点A,B,M与⊙C的位置关系如何
(2) 若以C为圆心作⊙C,使点A,B,M中至少有一点在圆内,且至少有一点在圆外,求⊙C的半径 r 的取值范围.
课堂练习
5.如图,已知矩形ABCD的边AB=3,AD=4.
(1) 以A为圆心,4为半径作⊙A,则点B,C,D与⊙A的位置关系如何?
解:AD=4= r,故D点在⊙A上,
AB=3< r, 故B点在⊙A内,
AC==5> r,故C点在⊙A外.
课堂练习
(2) 若以A点为圆心作⊙A,使B,C,D三点中至少有一点在圆内,且至少有一点在圆外,求⊙A的半径r的取值范围?(直接写出答案)
3
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
