4.3 角一课一练(含解析)
图片预览


文档简介
中小学教育资源及组卷应用平台
4.3角一课一练
一、单选题
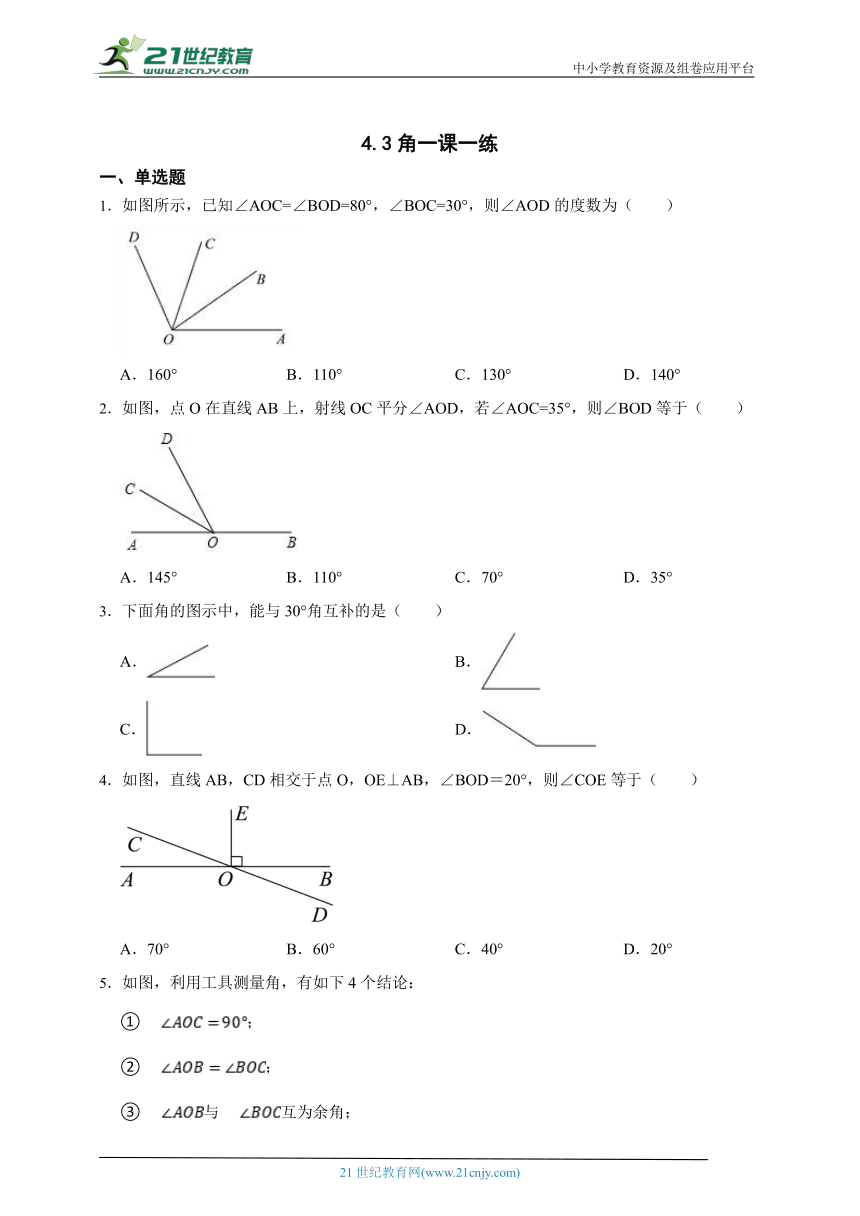
1.如图所示,已知∠AOC=∠BOD=80°,∠BOC=30°,则∠AOD的度数为( )
A.160° B.110° C.130° D.140°
2.如图,点O在直线AB上,射线OC平分∠AOD,若∠AOC=35°,则∠BOD等于( )
A.145° B.110° C.70° D.35°
3.下面角的图示中,能与30°角互补的是( )
A. B.
C. D.
4.如图,直线AB,CD相交于点O,OE⊥AB,∠BOD=20°,则∠COE等于( )
A.70° B.60° C.40° D.20°
5.如图,利用工具测量角,有如下4个结论:
①;
②;
③与互为余角;
④与互为补角.
上述结论中,所有正确结论的序号是( )
A.①②③ B.①② C.③④ D.①③④
二、填空题
6.如图,某海域有三个小岛A,B,O,在小岛O处观测到小岛A在它北偏东 的方向上,观测到小岛B在它南偏东 的方向上,则 的补角的度数是 .
三、计算题
7.
(1)2(-3xy+x2)-[2x2-3(5xy-2x2)-xy]
(2)计算:32°45′48″+21°25′14″
四、解答题
8.已知:如图,平分,将分为2:3两部分,,求的度数和的补角的度数.
五、作图题
9.作图分析题
已知:∠AOB,点P在OA上,请以P为顶点,PA为一边作∠APC=∠O(不写作法,但必须保留作图痕迹).
六、综合题
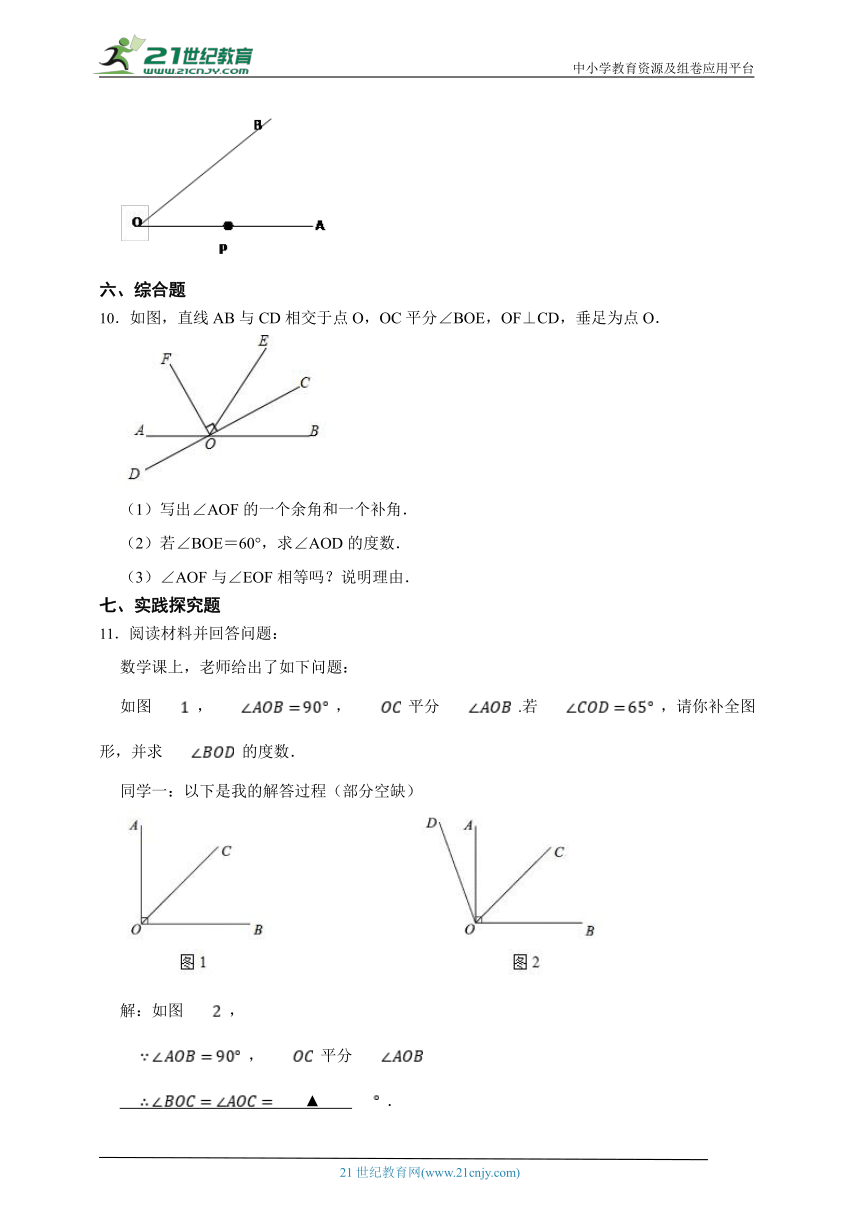
10.如图,直线AB与CD相交于点O,OC平分∠BOE,OF⊥CD,垂足为点O.
(1)写出∠AOF的一个余角和一个补角.
(2)若∠BOE=60°,求∠AOD的度数.
(3)∠AOF与∠EOF相等吗?说明理由.
七、实践探究题
11.阅读材料并回答问题:
数学课上,老师给出了如下问题:
如图 , , 平分 .若 ,请你补全图形,并求 的度数.
同学一:以下是我的解答过程(部分空缺)
解:如图 ,
, 平分
▲ .
,
▲ ▲ .
同学二:“符合题目要求的图形还有一种情况.”
请你完成以下问题:
(1)将同学一的解答过程空缺部分补充完整,能正确求出图 中 的度数.
(2)判断同学二的说法是否正确,若不正确,请说明理由;若正确,请你在图 1 中画出一种情况对应的图形,并求 的度数.
答案解析部分
1.【答案】C
【解析】【解答】因为∠AOC=80°,∠BOC=30°,
所以∠AOB=∠AOC-∠BOC=80°-30°=50°,
又因为∠BOD=80°,
所以∠AOD=∠AOB+∠BOD=50°+80°=130°.
故答案为:C.
【分析】由角的构成得∠AOB=∠AOC-∠BOC可求得∠AOB的度数,则根据∠AOD=∠AOB+∠BOD可求解.
2.【答案】B
【解析】【解答】解:∵射线OC平分∠DOA.
∴∠AOD=2∠AOC,
∵∠COA=35°,
∴∠DOA=70°,
∴∠BOD=180°﹣70°=110°,
故答案为:B.
【分析】根据角平分线求出∠AOD=2∠AOC,再求出∠DOA=70°,最后计算求解即可。
3.【答案】D
【解析】【解答】解:30°角的补角=180°﹣30°=150°,是钝角,
结合各图形,只有选项D是钝角,
所以,能与30°角互补的是选项D.
故选:D.
【分析】先求出30°的补角为150°,再测量度数等于150°的角即可求解.
4.【答案】A
【解析】【解答】∵∠AOC=∠BOD=20°,OE⊥AB,
∴∠AOC+∠COE=90°.
∴∠COE=90° ∠AOC=70°.
故答案为:A.
【分析】根据题意先求出∠AOC+∠COE=90°,再求解即可。
5.【答案】D
【解析】【解答】解:①由图可知,,故①符合题意;
②由图可知,,,
∴,故②不符合题意;
③∵,
∴与互为余角,故③符合题意;
④∵,,
∴,
∴与互为补角,故④符合题意;
综上分析可知①③④符合题意,故D符合题意.
故答案为:D.
【分析】根据角的定义、余角和补角的定义逐项判断即可。
6.【答案】
【解析】【解答】解:∵OA是表示北偏东 方向的一条射线,OB是表示南偏东38°12′方向的一条射线,
∴∠AOB=180°- -38°12′=78°56′,
∴∠AOB的补角的度数是180°-78°56′=101°4′.
故答案是:101°4′.
【分析】先求出∠AOB的度数,再利用补角的概念求解即可。
7.【答案】(1)解:2(-3xy+x2)-[2x2-3(5xy-2x2)-xy],
解:原式=-6xy+2x2-[2x2-15xy-6x2-xy],
=-6xy+2x2-2x2+15xy+6x2+xy,
=6x2+10xy,
(2)解:32°45′48″+21°25′14″,
=54°11′02″.
【解析】【分析】(1)先去小括号,再去中括号,最后合并同类项;(2)将度分秒按照单位对齐,从秒开始计算,逢60进1,依次计算即可.
8.【答案】解:∵平分
∴∠CBD=∠DBA
由题意,设∠ABE=,则∠CBE=,
∴∠ABC=,∠CBD=∠DBA=
∵
∴,,解得:
∴∠ABE=2×24=;∠ABC=5×24=
∴的补角的度数为
答:的度数为,的补角的度数为.
【解析】【分析】由角平分线的概念可得∠CBD=∠DBA,由题意设∠ABE=2x°,则∠CBE=3x°,∠ABC=5x°,∠CBD=∠DBA=x°,根据∠DBE=∠ABD-∠ABE=12°可得x,进而可求出∠ABE、∠ABC的度数,然后根据补角的概念可得∠ABE的补角的度数.
9.【答案】解:如图即为所求:
【解析】【分析】以点O为圆心,以任意长为半径画弧,交∠AOB的两边于两点;以点P为圆心,刚才的半径为半径,交射线PA于一点,以这点为圆心,∠AOB两边上两点的距离为半径画弧,交前弧于一点,过这点作射线PC,∠APC就是所求的角.
10.【答案】(1)解:∵OC⊥CD,
∴∠DOF=90°,
∴∠AOF+∠AOD=90°,
又∵∠BOC=∠AOD,
∴∠AOF+∠BOC=90°,
∵OC平分∠BOE,
∴∠COE=∠BOC,
∴∠AOF+∠COE=90°;
∴∠AOF的余角是,∠COE,∠BOC,∠AOD;
∵∠AOF+∠BOF=180°,
∴∠AOF的补角是∠BOF
(2)解:∵OC平分∠BOE,∠BOE=60°,
∴∠BOC=30°,
又∵∠AOD=∠BOC,
∴∠AOD=30°
(3)解:∠AOF=∠EOF,理由如下:
由(1)可得∠AOD=∠BOC=∠COE,
∵OF⊥OC,
∴∠DOF=∠COF=90°,
∴∠AOD+∠AOF=∠EOF+∠COE=90°,
∴∠AOF=∠EOF
【解析】【分析】(1)先求出 ∠AOF+∠BOC=90°, 再求出 ∠AOF+∠COE=90° ,最后求解即可;
(2)先求出 ∠BOC=30°, 再根据 ∠AOD=∠BOC求解即可;
(3)根据题意求出∠DOF=∠COF=90°, 再求出 ∠AOD+∠AOF=90°即可作答。
11.【答案】(1)解: , 平分
.
,
.
即 .
(2)解:正确.所画图形为:
, 平分 ,
.
,
.
【解析】【分析】(1) 根据角平分线及角的和差运算可得答案;
(2)根据角平分线的定义及角的和差运算求解即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
4.3角一课一练
一、单选题
1.如图所示,已知∠AOC=∠BOD=80°,∠BOC=30°,则∠AOD的度数为( )
A.160° B.110° C.130° D.140°
2.如图,点O在直线AB上,射线OC平分∠AOD,若∠AOC=35°,则∠BOD等于( )
A.145° B.110° C.70° D.35°
3.下面角的图示中,能与30°角互补的是( )
A. B.
C. D.
4.如图,直线AB,CD相交于点O,OE⊥AB,∠BOD=20°,则∠COE等于( )
A.70° B.60° C.40° D.20°
5.如图,利用工具测量角,有如下4个结论:
①;
②;
③与互为余角;
④与互为补角.
上述结论中,所有正确结论的序号是( )
A.①②③ B.①② C.③④ D.①③④
二、填空题
6.如图,某海域有三个小岛A,B,O,在小岛O处观测到小岛A在它北偏东 的方向上,观测到小岛B在它南偏东 的方向上,则 的补角的度数是 .
三、计算题
7.
(1)2(-3xy+x2)-[2x2-3(5xy-2x2)-xy]
(2)计算:32°45′48″+21°25′14″
四、解答题
8.已知:如图,平分,将分为2:3两部分,,求的度数和的补角的度数.
五、作图题
9.作图分析题
已知:∠AOB,点P在OA上,请以P为顶点,PA为一边作∠APC=∠O(不写作法,但必须保留作图痕迹).
六、综合题
10.如图,直线AB与CD相交于点O,OC平分∠BOE,OF⊥CD,垂足为点O.
(1)写出∠AOF的一个余角和一个补角.
(2)若∠BOE=60°,求∠AOD的度数.
(3)∠AOF与∠EOF相等吗?说明理由.
七、实践探究题
11.阅读材料并回答问题:
数学课上,老师给出了如下问题:
如图 , , 平分 .若 ,请你补全图形,并求 的度数.
同学一:以下是我的解答过程(部分空缺)
解:如图 ,
, 平分
▲ .
,
▲ ▲ .
同学二:“符合题目要求的图形还有一种情况.”
请你完成以下问题:
(1)将同学一的解答过程空缺部分补充完整,能正确求出图 中 的度数.
(2)判断同学二的说法是否正确,若不正确,请说明理由;若正确,请你在图 1 中画出一种情况对应的图形,并求 的度数.
答案解析部分
1.【答案】C
【解析】【解答】因为∠AOC=80°,∠BOC=30°,
所以∠AOB=∠AOC-∠BOC=80°-30°=50°,
又因为∠BOD=80°,
所以∠AOD=∠AOB+∠BOD=50°+80°=130°.
故答案为:C.
【分析】由角的构成得∠AOB=∠AOC-∠BOC可求得∠AOB的度数,则根据∠AOD=∠AOB+∠BOD可求解.
2.【答案】B
【解析】【解答】解:∵射线OC平分∠DOA.
∴∠AOD=2∠AOC,
∵∠COA=35°,
∴∠DOA=70°,
∴∠BOD=180°﹣70°=110°,
故答案为:B.
【分析】根据角平分线求出∠AOD=2∠AOC,再求出∠DOA=70°,最后计算求解即可。
3.【答案】D
【解析】【解答】解:30°角的补角=180°﹣30°=150°,是钝角,
结合各图形,只有选项D是钝角,
所以,能与30°角互补的是选项D.
故选:D.
【分析】先求出30°的补角为150°,再测量度数等于150°的角即可求解.
4.【答案】A
【解析】【解答】∵∠AOC=∠BOD=20°,OE⊥AB,
∴∠AOC+∠COE=90°.
∴∠COE=90° ∠AOC=70°.
故答案为:A.
【分析】根据题意先求出∠AOC+∠COE=90°,再求解即可。
5.【答案】D
【解析】【解答】解:①由图可知,,故①符合题意;
②由图可知,,,
∴,故②不符合题意;
③∵,
∴与互为余角,故③符合题意;
④∵,,
∴,
∴与互为补角,故④符合题意;
综上分析可知①③④符合题意,故D符合题意.
故答案为:D.
【分析】根据角的定义、余角和补角的定义逐项判断即可。
6.【答案】
【解析】【解答】解:∵OA是表示北偏东 方向的一条射线,OB是表示南偏东38°12′方向的一条射线,
∴∠AOB=180°- -38°12′=78°56′,
∴∠AOB的补角的度数是180°-78°56′=101°4′.
故答案是:101°4′.
【分析】先求出∠AOB的度数,再利用补角的概念求解即可。
7.【答案】(1)解:2(-3xy+x2)-[2x2-3(5xy-2x2)-xy],
解:原式=-6xy+2x2-[2x2-15xy-6x2-xy],
=-6xy+2x2-2x2+15xy+6x2+xy,
=6x2+10xy,
(2)解:32°45′48″+21°25′14″,
=54°11′02″.
【解析】【分析】(1)先去小括号,再去中括号,最后合并同类项;(2)将度分秒按照单位对齐,从秒开始计算,逢60进1,依次计算即可.
8.【答案】解:∵平分
∴∠CBD=∠DBA
由题意,设∠ABE=,则∠CBE=,
∴∠ABC=,∠CBD=∠DBA=
∵
∴,,解得:
∴∠ABE=2×24=;∠ABC=5×24=
∴的补角的度数为
答:的度数为,的补角的度数为.
【解析】【分析】由角平分线的概念可得∠CBD=∠DBA,由题意设∠ABE=2x°,则∠CBE=3x°,∠ABC=5x°,∠CBD=∠DBA=x°,根据∠DBE=∠ABD-∠ABE=12°可得x,进而可求出∠ABE、∠ABC的度数,然后根据补角的概念可得∠ABE的补角的度数.
9.【答案】解:如图即为所求:
【解析】【分析】以点O为圆心,以任意长为半径画弧,交∠AOB的两边于两点;以点P为圆心,刚才的半径为半径,交射线PA于一点,以这点为圆心,∠AOB两边上两点的距离为半径画弧,交前弧于一点,过这点作射线PC,∠APC就是所求的角.
10.【答案】(1)解:∵OC⊥CD,
∴∠DOF=90°,
∴∠AOF+∠AOD=90°,
又∵∠BOC=∠AOD,
∴∠AOF+∠BOC=90°,
∵OC平分∠BOE,
∴∠COE=∠BOC,
∴∠AOF+∠COE=90°;
∴∠AOF的余角是,∠COE,∠BOC,∠AOD;
∵∠AOF+∠BOF=180°,
∴∠AOF的补角是∠BOF
(2)解:∵OC平分∠BOE,∠BOE=60°,
∴∠BOC=30°,
又∵∠AOD=∠BOC,
∴∠AOD=30°
(3)解:∠AOF=∠EOF,理由如下:
由(1)可得∠AOD=∠BOC=∠COE,
∵OF⊥OC,
∴∠DOF=∠COF=90°,
∴∠AOD+∠AOF=∠EOF+∠COE=90°,
∴∠AOF=∠EOF
【解析】【分析】(1)先求出 ∠AOF+∠BOC=90°, 再求出 ∠AOF+∠COE=90° ,最后求解即可;
(2)先求出 ∠BOC=30°, 再根据 ∠AOD=∠BOC求解即可;
(3)根据题意求出∠DOF=∠COF=90°, 再求出 ∠AOD+∠AOF=90°即可作答。
11.【答案】(1)解: , 平分
.
,
.
即 .
(2)解:正确.所画图形为:
, 平分 ,
.
,
.
【解析】【分析】(1) 根据角平分线及角的和差运算可得答案;
(2)根据角平分线的定义及角的和差运算求解即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
