人教版数学八年级上册13.1.2.2 画轴对称图形的对称轴课件(共14张PPT)
文档属性
| 名称 | 人教版数学八年级上册13.1.2.2 画轴对称图形的对称轴课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-24 10:31:23 | ||
图片预览






文档简介
(共14张PPT)
13.1.2.2 画轴对称图形的对称轴
1.能依据轴对称的性质找出轴对称图形的对称轴;
2.能作出轴对称图形的对称轴,即线段垂直平分线的尺规作图.
3.与角平分线的性质结合解决生活中的问题.
学 习 目 标
通过前面的学习,我们知道一个轴对称图形的对称轴可能只有一条.也可能有许多条,如果给出一个轴对称图形,如何找出它的对称轴呢 这节课我们就来研究这个问题.
复 习 导 入
做轴对称图形的对称轴
问题1:有时我们感觉两个平面图形是轴对称的,如何验证呢 不折叠图形能准确地作出轴对称图形的对称轴吗
如果两个图形成轴对称,其对称轴就是任何一对对应点所连线段的垂直平分线,因此,我们只要找到一对应点,作出连接它们的线段的垂直平分可以得到这两个图形的对称轴.
A
B
C
A′
C′
B′
合 作 探 究
如图,点A和点B关于某条直线成轴对称,你能作出这条直线吗?
C
A
B
(2)作直线CD.
作法: (1) 连接AB,分别以点A和点B为圆心,大于 AB的长为半径画弧(想一想为什么),两弧相交于点C、D两点.
D
直线CD就是所求作的垂线.
这个作法实际上就是线段垂直平分线的尺规作图.我们也可以用这种方法确定线段的中点.
典 例 精 析
问题2: 对于轴对称图形,我们作出它们的
对称轴?
如图中的五角星,你能作出它的对称轴吗?
对于轴对称图形,只要找到任意一组对应点,作出对应点所连线段的垂直平分线,就得到此图形的对称轴.
图中的五角星,我们可以找出它的一对对应点A和A′,连接AA′,作出线段AA′的垂直平分线,则就是这个五角星的条对称轴.
A
A′
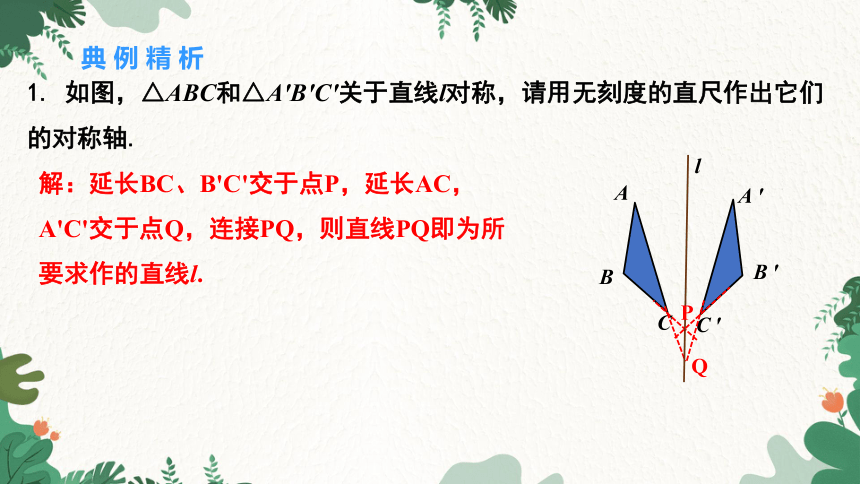
1. 如图,△ABC和△A′B′C′关于直线l对称,请用无刻度的直尺作出它们的对称轴.
解:延长BC、B'C'交于点P,延长AC,A'C'交于点Q,连接PQ,则直线PQ即为所要求作的直线l.
A
B
C
A ′
B ′
C ′
l
P
Q
典 例 精 析
2. 作出下列图形的一条对称轴.和同学比较一下,你们作出的对称轴一样吗?
(1)作对称轴的依据:
如果一个图形是轴对称图形或两个图形成轴对称,其对称轴就是任何一对对应点所连线段的垂直平分线;
(2)作对称轴的步骤:
①找:找到轴对称图形或成轴对称的两个图形的任意一对对应点;
②连:连接这对对应点;
③作:作出对应点所连线段的垂直平分线这条垂直平分线就是该轴对称图形或成轴对称的两个图形的对称轴.
新 知 小 结
1.如图,在△ABC中,分别以点A,B为圆心,大于 AB长为半径画弧,两弧分别交于点D,E,则直线DE是( )
A.∠A的平分线
B.AC边的中线
C.BC边的高线
D.AB边的垂直平分线
D
随 堂 练 习
2.如图,已知线段AB的垂直平分线CP交AB于点P,且AP=2PC,现欲在线段AB上求作两点D,E,使其满足AD=DC=CE=EB,对于以下甲、乙两种作法:甲:分别作∠ACP、∠BCP的平分线,分别交AB于D、E,则D、E即为所求;乙:分别作AC、BC的垂直平分线,分别交AB于D、E,则D、E两点即为所求.下列说法正确的是( )
A.甲、乙都正确
B.甲、乙都错误
C.甲正确,乙错误
D.甲错误,乙正确
D
角是轴对称图形,角平分线所在的直线就是角的对称轴.
3. 如图,角是轴对称图形吗?如果是,它的对称轴是什么?
作轴对称图形的对称轴
1.作线段的垂直平分线.
2.与角平分线的性质结合解决生活中的问题.
课 堂 总 结
谢谢大家!
13.1.2.2 画轴对称图形的对称轴
1.能依据轴对称的性质找出轴对称图形的对称轴;
2.能作出轴对称图形的对称轴,即线段垂直平分线的尺规作图.
3.与角平分线的性质结合解决生活中的问题.
学 习 目 标
通过前面的学习,我们知道一个轴对称图形的对称轴可能只有一条.也可能有许多条,如果给出一个轴对称图形,如何找出它的对称轴呢 这节课我们就来研究这个问题.
复 习 导 入
做轴对称图形的对称轴
问题1:有时我们感觉两个平面图形是轴对称的,如何验证呢 不折叠图形能准确地作出轴对称图形的对称轴吗
如果两个图形成轴对称,其对称轴就是任何一对对应点所连线段的垂直平分线,因此,我们只要找到一对应点,作出连接它们的线段的垂直平分可以得到这两个图形的对称轴.
A
B
C
A′
C′
B′
合 作 探 究
如图,点A和点B关于某条直线成轴对称,你能作出这条直线吗?
C
A
B
(2)作直线CD.
作法: (1) 连接AB,分别以点A和点B为圆心,大于 AB的长为半径画弧(想一想为什么),两弧相交于点C、D两点.
D
直线CD就是所求作的垂线.
这个作法实际上就是线段垂直平分线的尺规作图.我们也可以用这种方法确定线段的中点.
典 例 精 析
问题2: 对于轴对称图形,我们作出它们的
对称轴?
如图中的五角星,你能作出它的对称轴吗?
对于轴对称图形,只要找到任意一组对应点,作出对应点所连线段的垂直平分线,就得到此图形的对称轴.
图中的五角星,我们可以找出它的一对对应点A和A′,连接AA′,作出线段AA′的垂直平分线,则就是这个五角星的条对称轴.
A
A′
1. 如图,△ABC和△A′B′C′关于直线l对称,请用无刻度的直尺作出它们的对称轴.
解:延长BC、B'C'交于点P,延长AC,A'C'交于点Q,连接PQ,则直线PQ即为所要求作的直线l.
A
B
C
A ′
B ′
C ′
l
P
Q
典 例 精 析
2. 作出下列图形的一条对称轴.和同学比较一下,你们作出的对称轴一样吗?
(1)作对称轴的依据:
如果一个图形是轴对称图形或两个图形成轴对称,其对称轴就是任何一对对应点所连线段的垂直平分线;
(2)作对称轴的步骤:
①找:找到轴对称图形或成轴对称的两个图形的任意一对对应点;
②连:连接这对对应点;
③作:作出对应点所连线段的垂直平分线这条垂直平分线就是该轴对称图形或成轴对称的两个图形的对称轴.
新 知 小 结
1.如图,在△ABC中,分别以点A,B为圆心,大于 AB长为半径画弧,两弧分别交于点D,E,则直线DE是( )
A.∠A的平分线
B.AC边的中线
C.BC边的高线
D.AB边的垂直平分线
D
随 堂 练 习
2.如图,已知线段AB的垂直平分线CP交AB于点P,且AP=2PC,现欲在线段AB上求作两点D,E,使其满足AD=DC=CE=EB,对于以下甲、乙两种作法:甲:分别作∠ACP、∠BCP的平分线,分别交AB于D、E,则D、E即为所求;乙:分别作AC、BC的垂直平分线,分别交AB于D、E,则D、E两点即为所求.下列说法正确的是( )
A.甲、乙都正确
B.甲、乙都错误
C.甲正确,乙错误
D.甲错误,乙正确
D
角是轴对称图形,角平分线所在的直线就是角的对称轴.
3. 如图,角是轴对称图形吗?如果是,它的对称轴是什么?
作轴对称图形的对称轴
1.作线段的垂直平分线.
2.与角平分线的性质结合解决生活中的问题.
课 堂 总 结
谢谢大家!
