数学人教A版(2019)必修第二册10.2事件的相互独立性(共27张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册10.2事件的相互独立性(共27张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-23 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
10.2 事件的相互独立性(二)
事件的相互独立性
1
启动思维
在一次有关“三国演义”的知识竞赛中,三个“臭皮匠”能答对该题目的概率分别为50%,45%,40%,“诸葛亮”能答对该题目的概率为80%,如果将“三个臭皮匠”组成一组与“诸葛亮”进行比赛,各选手独立答题,不得商量,团队中只要有一人答出即为该组获胜.
问:哪方获胜的可能性大?
略解: 三个“臭皮匠”中至少有一人答对的概率为
>P(D)
所以,“臭皮匠”获胜可能性大.
合 作 共 赢
知识回顾
2
1.相互独立的概念
(1)事件A与事件B相互独立,即事件A(或B)是否发生,对事件B(或A)发生的概率________.
(2)设A,B为两个事件,如果P(AB)= ________ ,
则称事件A与事件B相互独立.
2.相互独立的性质
(1)若事件A与B相互独立,那么 , , 也都相互独立.
没有影响
P(A)P(B)
(2)两个相互独立事件A,B同时发生,即事件AB发生的概率为_________________.这就是说,两个相互独立事件同时发生的概率等于
_________________________.
两个事件发生的概率的乘积
(可扩展到多个)
典例导航
3
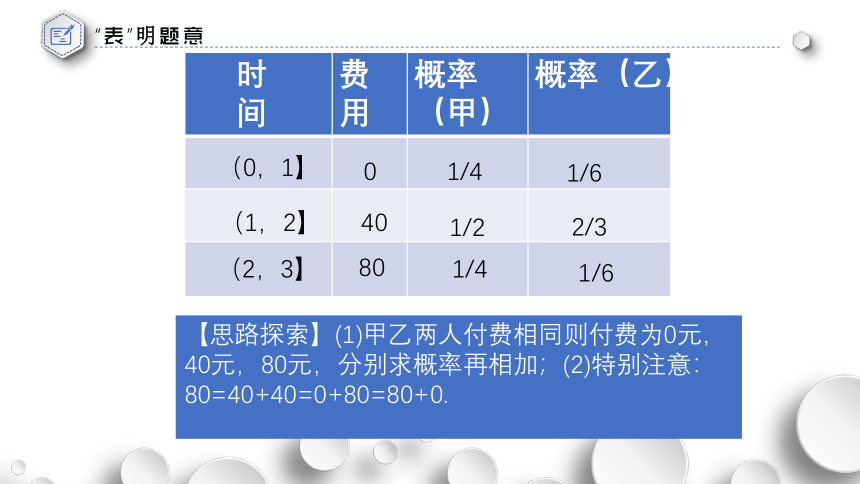
“表”明题意
时 间 费用 概率(甲) 概率(乙)
(0,1】
0
(1,2】
40
(2,3】
80
1/4
1/2
1/6
2/3
1/4
1/6
【思路探索】(1)甲乙两人付费相同则付费为0元,40元,80元,分别求概率再相加;(2)特别注意:80=40+40=0+80=80+0.
规范解答
设甲、乙两人所付的滑雪费用之和为80元的概率为P4
3
例2.11分制乒乓球比赛,每赢一球得1分,当某局打成10:10平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为0.5,乙发球时甲得分的概率为0.4,各球的结果相互独立.在某局双方10:10平后,甲先发球,两人又打了X个球该局比赛结束.
(1)求P(X=2);
(2)求事件“X=4且甲获胜”的概率.
典例导航
“表”明题意
(1)X=2
第几球
谁发球
1
2
甲
乙
谁胜
甲(0.5)
甲(0.4)
乙(0.5)
乙(0.6)
解析:
(1)X=2时,有两种可能:
①甲连赢两个球结束比赛,此时P1 =0.5×0.4=0.2 ,
②乙连赢两个球结束比赛,此时P2 =0.5×0.6=0.3
∴ P(X=2) =P1+P2=0.5
(2)X=4且甲获胜,即前两个球甲乙各胜一球,三四个球都是甲获胜,
此时P=(0.5×0.6+0.5×0.4)×0.5×0.4=0.1
思考:(1)第二问改为求P(X=4)如何解?
(2)X可能等于3吗?
规范解答
课堂小结
求相互独立事件概率的关键是读懂题意,对于较复杂的题可以通过列简表理清题意:
(1)求相互独立事件同时发生的概率的步骤是:①首先确定各事件之间是相互独立的;②确定这些事件可以同时发生;③求出每个事件的概率,再求积.
(2)使用相互独立事件同时发生的概率计算公式时,要掌握公式的适用条件——各个事件是相互独立的,而且它们同时发生.
4
谢谢大家
请完成配套练习
5
自主练习
5
自主练习
答案: D
5
自主练习
5
自主练习
答案: D
5
自主练习
5
自主练习
5
自主练习
5
自主练习
4.甲、乙2人各进行1次射击,如果2人击中目标的概率都是0.6,计算:
(1)2人都击中目标的概率;
(2)其中恰有1人击中目标的概率;
(3)至少有1人击中目标的概率.
解析: (1)记:“甲射击1次,击中目标”为事件A,“乙射击1次,击中目标”为事件B,则“2人都击中目标”为事件A·B
又∵P(A)=P(B)=0.6
∴P(A·B)=P(A)·P(B)=0.6×0.6=0.36.
5
自主练习
5
自主练习
5
自主练习
5
自主练习
5
自主练习
5
自主练习
5
自主练习
10.2 事件的相互独立性(二)
事件的相互独立性
1
启动思维
在一次有关“三国演义”的知识竞赛中,三个“臭皮匠”能答对该题目的概率分别为50%,45%,40%,“诸葛亮”能答对该题目的概率为80%,如果将“三个臭皮匠”组成一组与“诸葛亮”进行比赛,各选手独立答题,不得商量,团队中只要有一人答出即为该组获胜.
问:哪方获胜的可能性大?
略解: 三个“臭皮匠”中至少有一人答对的概率为
>P(D)
所以,“臭皮匠”获胜可能性大.
合 作 共 赢
知识回顾
2
1.相互独立的概念
(1)事件A与事件B相互独立,即事件A(或B)是否发生,对事件B(或A)发生的概率________.
(2)设A,B为两个事件,如果P(AB)= ________ ,
则称事件A与事件B相互独立.
2.相互独立的性质
(1)若事件A与B相互独立,那么 , , 也都相互独立.
没有影响
P(A)P(B)
(2)两个相互独立事件A,B同时发生,即事件AB发生的概率为_________________.这就是说,两个相互独立事件同时发生的概率等于
_________________________.
两个事件发生的概率的乘积
(可扩展到多个)
典例导航
3
“表”明题意
时 间 费用 概率(甲) 概率(乙)
(0,1】
0
(1,2】
40
(2,3】
80
1/4
1/2
1/6
2/3
1/4
1/6
【思路探索】(1)甲乙两人付费相同则付费为0元,40元,80元,分别求概率再相加;(2)特别注意:80=40+40=0+80=80+0.
规范解答
设甲、乙两人所付的滑雪费用之和为80元的概率为P4
3
例2.11分制乒乓球比赛,每赢一球得1分,当某局打成10:10平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为0.5,乙发球时甲得分的概率为0.4,各球的结果相互独立.在某局双方10:10平后,甲先发球,两人又打了X个球该局比赛结束.
(1)求P(X=2);
(2)求事件“X=4且甲获胜”的概率.
典例导航
“表”明题意
(1)X=2
第几球
谁发球
1
2
甲
乙
谁胜
甲(0.5)
甲(0.4)
乙(0.5)
乙(0.6)
解析:
(1)X=2时,有两种可能:
①甲连赢两个球结束比赛,此时P1 =0.5×0.4=0.2 ,
②乙连赢两个球结束比赛,此时P2 =0.5×0.6=0.3
∴ P(X=2) =P1+P2=0.5
(2)X=4且甲获胜,即前两个球甲乙各胜一球,三四个球都是甲获胜,
此时P=(0.5×0.6+0.5×0.4)×0.5×0.4=0.1
思考:(1)第二问改为求P(X=4)如何解?
(2)X可能等于3吗?
规范解答
课堂小结
求相互独立事件概率的关键是读懂题意,对于较复杂的题可以通过列简表理清题意:
(1)求相互独立事件同时发生的概率的步骤是:①首先确定各事件之间是相互独立的;②确定这些事件可以同时发生;③求出每个事件的概率,再求积.
(2)使用相互独立事件同时发生的概率计算公式时,要掌握公式的适用条件——各个事件是相互独立的,而且它们同时发生.
4
谢谢大家
请完成配套练习
5
自主练习
5
自主练习
答案: D
5
自主练习
5
自主练习
答案: D
5
自主练习
5
自主练习
5
自主练习
5
自主练习
4.甲、乙2人各进行1次射击,如果2人击中目标的概率都是0.6,计算:
(1)2人都击中目标的概率;
(2)其中恰有1人击中目标的概率;
(3)至少有1人击中目标的概率.
解析: (1)记:“甲射击1次,击中目标”为事件A,“乙射击1次,击中目标”为事件B,则“2人都击中目标”为事件A·B
又∵P(A)=P(B)=0.6
∴P(A·B)=P(A)·P(B)=0.6×0.6=0.36.
5
自主练习
5
自主练习
5
自主练习
5
自主练习
5
自主练习
5
自主练习
5
自主练习
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
