数学人教A版(2019)必修第一册3.4函数的应用(一)课件(共16张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册3.4函数的应用(一)课件(共16张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 570.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-23 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
第三章 函数的概念与性质
3.4 函数的应用(一)
1.能够利用给定的函数模型或建立函数模型解决实际问题.
2.经历建立函数模型解决实际问题的过程,提高综合运用数学知识和方法解决实际问题的能力.
3.体会函数模型在现实世界中的重要性.
学习目标
(1)我市有甲、乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同.甲家每张球台每小时5元;乙家按月计费,一个月中30小时以内(含30小时)每张球台90元,超过30小时的部分每张球台每小时2元.小张准备下个月从这两家中的一家租一张球台开展活动,其活动时间不少于15小时,也不超过40小时.
设在甲家租一张球台开展活动x小时的收费为f(x)元(15≤x≤40),在乙家租一张球台开展活动x小时的收费为g(x)元(15≤x≤40),试求f(x)和g(x).
一、引入新课
解:(1)f(x)=5x(15≤x≤40);
g(x)=
一、引入新课
(2)A、B两城相距100 km,在两地之间距A城x km处D地建一核电站给A、B两城供电.为保证城市安全,核电站距城市距离不得少于10 km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数λ=0.25.若A城供电量为20亿度/月,B城为10亿度/月.把月供电总费用 y表示成 x的函数,并求定义域.
一、引入新课
解:(2)y=5x2+(100—x)2(10≤x≤90).
解:(3)分别属于一次函数模型、分段函数、二次函数模型.
(3)分析以上实例属于哪种函数模型.
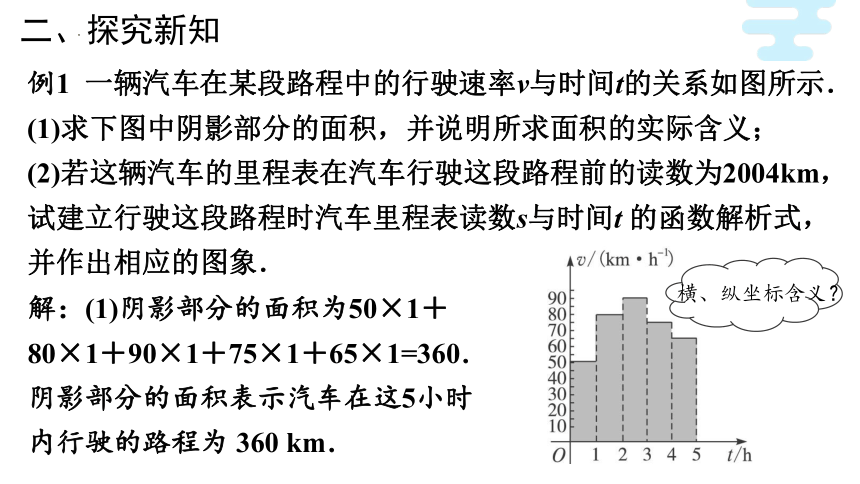
解:(1)阴影部分的面积为50×1+80×1+90×1+75×1+65×1=360.
阴影部分的面积表示汽车在这5小时内行驶的路程为 360 km.
横、纵坐标含义?
二、探究新知
例1 一辆汽车在某段路程中的行驶速率v与时间t的关系如图所示.
(1)求下图中阴影部分的面积,并说明所求面积的实际含义;
(2)若这辆汽车的里程表在汽车行驶这段路程前的读数为2004km,
试建立行驶这段路程时汽车里程表读数s与时间t 的函数解析式,
并作出相应的图象.
二、探究新知
解:
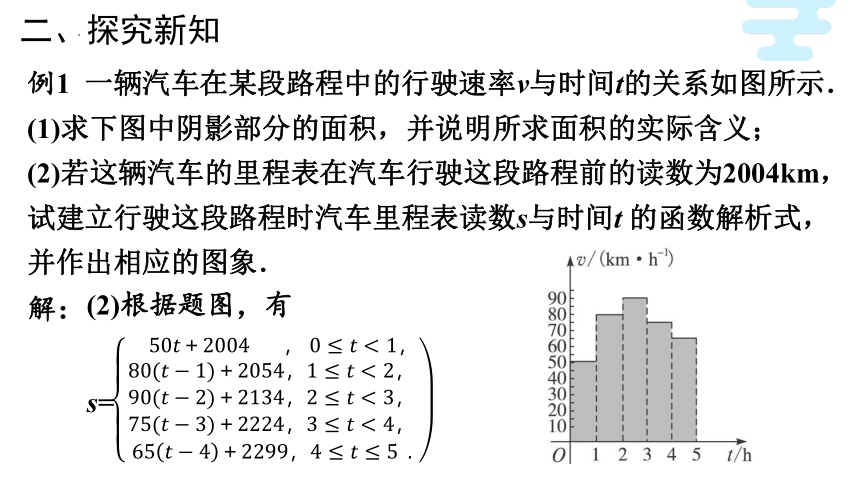
(2)根据题图,有
s=
例1 一辆汽车在某段路程中的行驶速率v与时间t的关系如图所示.
(1)求下图中阴影部分的面积,并说明所求面积的实际含义;
(2)若这辆汽车的里程表在汽车行驶这段路程前的读数为2004km,
试建立行驶这段路程时汽车里程表读数s与时间t 的函数解析式,
并作出相应的图象.
二、探究新知
例1 一辆汽车在某段路程中的行驶速率v与时间t的关系如图所示.
(1)求下图中阴影部分的面积,并说明所求面积的实际含义;
(2)若这辆汽车的里程表在汽车行驶这段路程前的读数为2004km,
试建立行驶这段路程时汽车里程表读数s与时间t 的函数解析式,
并作出相应的图象.
解:
(2)这个函数的图象如下图所示.
1.解决函数应用问题的步骤
(1)审题:弄清题意,分清条件和结论,理顺数量关系,初步选择数学模型.
(2)建模:将自然语言转化为数学语言,将文字语言转化为符号语言,利用数学知识,建立相应的数学模型.
(3)解模:求解数学模型,得出数学结论.
(4)还原:将数学问题还原为实际问题的意义.
三、强化理解
注意定义域.
函数模型 函数解析式
一次函数模型 f(x)=ax+b(a,b为常数,a≠0)
二次函数模型 f(x)=ax2+bx+c(a,b,c为常数,a≠0)
反比例函数模型 f(x)=(k为常数,且k≠0)
幂函数模型 f(x)=xα(α为常数,α≠0)
2.几种常见的函数模型
三、强化理解
例2 为了保护环境,发展低碳经济,某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本 y(单位:元)与月处理量x(单位:吨)之间的函数关系可近似的表示为 y=x2-200x+80 000,且每处理一吨二氧化碳得到可利用的化工产品的价值为100元,则该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?
四、新知应用
解:设该单位每月获利为S,则
S=100x-y
=100x-(x2-200x+80 000)
=-x2+300x-80 000
=-(x-300)2-35 000,
因为400≤x≤600,所以当x=400时,S有最大值-40 000.
故该单位不获利,需要国家每月至少补贴40 000元,才能
不亏损.
四、新知应用
某厂生产某种产品x(单位:百台),总成本为C(x)(单位:万元),其中固定成本为2万元,每生产1百台,成本增加1万元,销售收入为R(x)(单位:万元),且R(x)=假定该产品产销平衡.
(1)若要该厂不亏本,产量x应控制在什么范围内?
(2)该厂生产多少台时,可使利润最大?
(3)求该厂利润最大时产品的售价.
五、课堂练习
解:由题意得,成本函数C(x)=2+x,从而利润函数
L(x)=R(x)-C(x)=
(1)要使该厂不亏本,只要L(x)≥0.
①当0≤x≤4时,由L(x)≥0,得3x-0.5x2-2.5≥0,解得1≤x≤4;
②当x>4时,由L(x)≥0,得5.5-x≥0,解得4综上,1≤x≤5.5.
故若要该厂不亏本,产量x应控制在100台到550台之间.
五、课堂练习
(2)当0≤x≤4时,L(x)=-0.5(x-3)2+2,
故当x=3时,L(x)max=2;
当x>4时,L(x)<1.5<2.
综上,当生产300台时,可使利润最大.
(3)由(2)知 x=3时,利润最大,
此时的售价P==2.33(万元/百台)=233(元/台).
五、课堂练习
回顾讨论,总结本节课学习内容:
1.知识:函数的应用;
2.思想:数形结合.
六、归纳小结
第三章 函数的概念与性质
3.4 函数的应用(一)
1.能够利用给定的函数模型或建立函数模型解决实际问题.
2.经历建立函数模型解决实际问题的过程,提高综合运用数学知识和方法解决实际问题的能力.
3.体会函数模型在现实世界中的重要性.
学习目标
(1)我市有甲、乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同.甲家每张球台每小时5元;乙家按月计费,一个月中30小时以内(含30小时)每张球台90元,超过30小时的部分每张球台每小时2元.小张准备下个月从这两家中的一家租一张球台开展活动,其活动时间不少于15小时,也不超过40小时.
设在甲家租一张球台开展活动x小时的收费为f(x)元(15≤x≤40),在乙家租一张球台开展活动x小时的收费为g(x)元(15≤x≤40),试求f(x)和g(x).
一、引入新课
解:(1)f(x)=5x(15≤x≤40);
g(x)=
一、引入新课
(2)A、B两城相距100 km,在两地之间距A城x km处D地建一核电站给A、B两城供电.为保证城市安全,核电站距城市距离不得少于10 km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数λ=0.25.若A城供电量为20亿度/月,B城为10亿度/月.把月供电总费用 y表示成 x的函数,并求定义域.
一、引入新课
解:(2)y=5x2+(100—x)2(10≤x≤90).
解:(3)分别属于一次函数模型、分段函数、二次函数模型.
(3)分析以上实例属于哪种函数模型.
解:(1)阴影部分的面积为50×1+80×1+90×1+75×1+65×1=360.
阴影部分的面积表示汽车在这5小时内行驶的路程为 360 km.
横、纵坐标含义?
二、探究新知
例1 一辆汽车在某段路程中的行驶速率v与时间t的关系如图所示.
(1)求下图中阴影部分的面积,并说明所求面积的实际含义;
(2)若这辆汽车的里程表在汽车行驶这段路程前的读数为2004km,
试建立行驶这段路程时汽车里程表读数s与时间t 的函数解析式,
并作出相应的图象.
二、探究新知
解:
(2)根据题图,有
s=
例1 一辆汽车在某段路程中的行驶速率v与时间t的关系如图所示.
(1)求下图中阴影部分的面积,并说明所求面积的实际含义;
(2)若这辆汽车的里程表在汽车行驶这段路程前的读数为2004km,
试建立行驶这段路程时汽车里程表读数s与时间t 的函数解析式,
并作出相应的图象.
二、探究新知
例1 一辆汽车在某段路程中的行驶速率v与时间t的关系如图所示.
(1)求下图中阴影部分的面积,并说明所求面积的实际含义;
(2)若这辆汽车的里程表在汽车行驶这段路程前的读数为2004km,
试建立行驶这段路程时汽车里程表读数s与时间t 的函数解析式,
并作出相应的图象.
解:
(2)这个函数的图象如下图所示.
1.解决函数应用问题的步骤
(1)审题:弄清题意,分清条件和结论,理顺数量关系,初步选择数学模型.
(2)建模:将自然语言转化为数学语言,将文字语言转化为符号语言,利用数学知识,建立相应的数学模型.
(3)解模:求解数学模型,得出数学结论.
(4)还原:将数学问题还原为实际问题的意义.
三、强化理解
注意定义域.
函数模型 函数解析式
一次函数模型 f(x)=ax+b(a,b为常数,a≠0)
二次函数模型 f(x)=ax2+bx+c(a,b,c为常数,a≠0)
反比例函数模型 f(x)=(k为常数,且k≠0)
幂函数模型 f(x)=xα(α为常数,α≠0)
2.几种常见的函数模型
三、强化理解
例2 为了保护环境,发展低碳经济,某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本 y(单位:元)与月处理量x(单位:吨)之间的函数关系可近似的表示为 y=x2-200x+80 000,且每处理一吨二氧化碳得到可利用的化工产品的价值为100元,则该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?
四、新知应用
解:设该单位每月获利为S,则
S=100x-y
=100x-(x2-200x+80 000)
=-x2+300x-80 000
=-(x-300)2-35 000,
因为400≤x≤600,所以当x=400时,S有最大值-40 000.
故该单位不获利,需要国家每月至少补贴40 000元,才能
不亏损.
四、新知应用
某厂生产某种产品x(单位:百台),总成本为C(x)(单位:万元),其中固定成本为2万元,每生产1百台,成本增加1万元,销售收入为R(x)(单位:万元),且R(x)=假定该产品产销平衡.
(1)若要该厂不亏本,产量x应控制在什么范围内?
(2)该厂生产多少台时,可使利润最大?
(3)求该厂利润最大时产品的售价.
五、课堂练习
解:由题意得,成本函数C(x)=2+x,从而利润函数
L(x)=R(x)-C(x)=
(1)要使该厂不亏本,只要L(x)≥0.
①当0≤x≤4时,由L(x)≥0,得3x-0.5x2-2.5≥0,解得1≤x≤4;
②当x>4时,由L(x)≥0,得5.5-x≥0,解得4
故若要该厂不亏本,产量x应控制在100台到550台之间.
五、课堂练习
(2)当0≤x≤4时,L(x)=-0.5(x-3)2+2,
故当x=3时,L(x)max=2;
当x>4时,L(x)<1.5<2.
综上,当生产300台时,可使利润最大.
(3)由(2)知 x=3时,利润最大,
此时的售价P==2.33(万元/百台)=233(元/台).
五、课堂练习
回顾讨论,总结本节课学习内容:
1.知识:函数的应用;
2.思想:数形结合.
六、归纳小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
