2023-2024学年河北省秦皇岛市新世纪高级中学高二(上)开学数学试卷(含解析)
文档属性
| 名称 | 2023-2024学年河北省秦皇岛市新世纪高级中学高二(上)开学数学试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 384.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-23 13:45:49 | ||
图片预览




文档简介
2023-2024学年河北省秦皇岛市新世纪高级中学高二(上)开学数学试卷
一、单选题(本大题共8小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1. 已知,为虚数单位,则( )
A. B. C. D.
2. 在中,内角,,所对的边为,,,若,,,则( )
A. B. 或 C. D. 或
3. 若一个样本容量为的样本的平均数为,方差为现样本中又加入一个新数据,此时样本容量为,平均数为,方差为,则( )
A. , B. , C. , D. ,
4. 如图,在梯形中,,,设,,则( )
A. B. C. D.
5. 若,,则( )
A. B. C. D.
6. 已知,则( )
A. B.
C. D.
7. 海伦公式是利用三角形的三条边的边长,,直接求三角形面积的公式,表达式为:,;它的特点是形式漂亮,便于记忆.中国宋代的数学家秦九韶在年独立提出了“三斜求积术”,虽然它与海伦公式形式上有所不同,但它与海伦公式完全等价,因此海伦公式又译作海伦秦九韶公式.现在有周长为的满足::::,则用以上给出的公式求得的面积为( )
A. B. C. D.
8. 已知函数, 为的零点,为图象的对称轴,且在上单调,则的最大值为( )
A. B. C. D.
二、多选题(本大题共4小题,共20.0分。在每小题有多项符合题目要求)
9. 复数,是虚数单位,则下列结论正确的是( )
A. B. 的共轭复数为
C. 的实部与虚部之和为 D. 在复平面内的对应点位于第一象限
10. 下列函数中是奇函数,且最小正周期是的函数是( )
A. B.
C. D.
11. 已知函数的部分图象如图所示,下列说法正确的是( )
A. 函数的最小正周期为
B. 函数在单调递减
C. 函数的图象关于直线对称
D. 该图象向右平移个单位可得的图象
12. 三角形的三边,,所对的角为,,,,则下列说法正确的是( )
A.
B. 若面积为,则周长的最小值为
C. 当,时,
D. 若,,则面积为
三、填空题(本大题共4小题,共20.0分)
13. 某校共有师生人,其中教师人,男学生人,女学生人.现用比例分配的分层随机抽样方法从所有师生中抽取一个容量为的样本,已知从女学生中抽取的人数为,那么______.
14. ______ .
15. 在边长为的正中,若点满足,则 ______ .
16. 在中,,,为边上的中点,且的长度为,则 ______ .
四、解答题(本大题共6小题,共70.0分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
设向量满足,,.
求向量,的夹角及;
若,则实数的值.
18. 本小题分
的内角,,的对边分别为,,,已知.
Ⅰ求;
Ⅱ若,,求,的值.
19. 本小题分
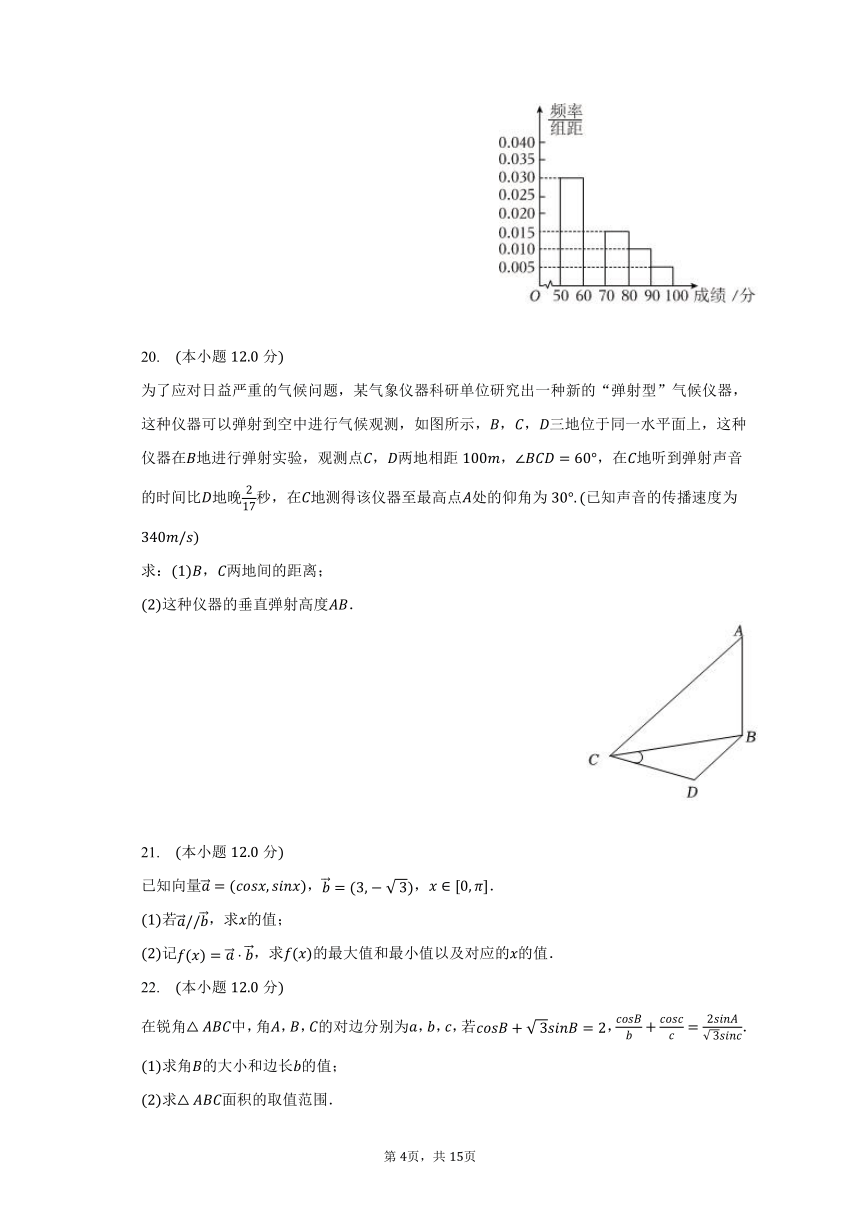
年月日,神舟十五号载人飞船返回舱在预定区域成功着陆,航天员费俊龙,邓清明,张陆顺利出舱,神舟十五号载人飞行任务圆满完成为纪念中国航天事业所取得的成就,发扬并传承中国航天精神,某市随机抽取名学生进行了航天知识竞赛并记录得分满分:分,将学生的成绩整理后分成五组,从左到右依次记为,,,,,并绘制成如图所示的频率分布直方图.
请补全频率分布直方图;
估计这名学生成绩的众数、平均数和计算分位数求平均值时同一组数据用该组区间的中点值作代表,分位数小数点后面保留两位有效数字.
20. 本小题分
为了应对日益严重的气候问题,某气象仪器科研单位研究出一种新的“弹射型”气候仪器,这种仪器可以弹射到空中进行气候观测,如图所示,,,三地位于同一水平面上,这种仪器在地进行弹射实验,观测点,两地相距,,在地听到弹射声音的时间比地晚秒,在地测得该仪器至最高点处的仰角为已知声音的传播速度为
求:,两地间的距离;
这种仪器的垂直弹射高度.
21. 本小题分
已知向量,,.
若,求的值;
记,求的最大值和最小值以及对应的的值.
22. 本小题分
在锐角中,角,,的对边分别为,,,若,.
求角的大小和边长的值;
求面积的取值范围.
答案和解析
1.【答案】
【解析】解:因为,即,
由复数相等的定义可得,,即.
故选:.
利用复数相等的定义求解即可.
本题考查了复数相等定义的理解和应用,属于基础题.
2.【答案】
【解析】解:因为,,,
所以由正弦定理有:,
所以,
因为,所以,
所以.
故选:.
由正弦定理可得,再结合大边对大角即可求得.
本题考查正弦定理的应用,属于基础题.
3.【答案】
【解析】解:某个数据的平均数为,方差为,现又加入一个新数据,
此时这个数的平均数为,方差为,
,.
故选:.
利用平均数、方差的定义直接求解.
本题考查平均数、方差的求法,考查推理论证能力、运算求解能力,考查化归与转化思想,是基础题.
4.【答案】
【解析】【分析】
本题主要考查了平面向量的基本运算,属于基础试题.
取中点,由可知,从而可得四边形为平行四边形,结合向量的基本运算即可求解.
【解答】
解:取中点,由可知,
四边形为平行四边形,
则.
故选:.
5.【答案】
【解析】解:因为,,
所以,,
所以.
故选:.
由已知利用同角三角函数基本关系式可求的值,进而利用诱导公式,二倍角的正切函数公式即可计算得解.
本题主要考查了同角三角函数基本关系式,诱导公式,二倍角的正切函数公式在三角函数化简求值中的应用,考查了转化思想,属于基础题.
6.【答案】
【解析】【分析】
利用三角形法则可求得,由向量共线条件可得与共线,从而可得结论.本题考查向量共线的条件,属基础题,熟记向量共线的充要条件是解决问题的关键.
【解答】
解:,
又,所以,则与共线,
又与有公共点,
所以、、三点共线.
故选A.
7.【答案】
【解析】解:::::,::::,
周长为,即,
,,,,
的面积.
故选:.
由正弦定理得三角形三边之比,由周长求出三边,代入公式即可.
本题考查了数学文化,考查了正弦定理、三角形面积公式在解三角形中的应用,考查了计算能力和转化思想,属于基础题.
8.【答案】
【解析】【分析】
本题考查三角函数的图象和性质的综合运用,属于较难题目.
结合为的零点,为图象的对称轴,可得为正奇数,且,结合在上单调,可得的最大值.
【解答】
解:为的零点,为图象的对称轴,
,即,,
即,,即为正奇数,
在上单调,则,
即,解得:,
当时,,,
,,
此时在不单调,不满足题意;
当时,,,
,,
此时在单调,满足题意;
故的最大值为,
故选B.
9.【答案】
【解析】解:,
对于,,故A错误,
对于,的共轭复数为,故B错误,
对于,的实部与虚部之和为,故C正确,
对于,在复平面内的对应点位于第一象限,故D正确.
故选:.
根据已知条件,先对化简,再结合复数模公式,共轭复数的定义,实部和虚部的定义,复数的几何意义,即可求解.
本题主要考查复数模公式,共轭复数的定义,实部和虚部的定义,复数的几何意义,属于基础题.
10.【答案】
【解析】解:对于,函数既是奇函数,函数的最小正周期也为,故A正确;
对于:函数不是周期函数,故B错误;
对于:既是奇函数,函数的最小正周期也为,故C正确;
对于:函数为偶函数,故D错误.
故选:.
直接利用函数的奇偶性和周期性判断结果.
本题考查的知识要点:函数的奇偶性和周期性,主要考查学生的理解能力和计算能力,属于中档题.
11.【答案】
【解析】解:由图象可知:,周期,
;
由,解得:,
故函数.
对于:,故A错误;
对于:当时,因为上正弦函数先减后增,不单调,所以在上不单调,故B错误;
对于:当时,即直线是的一条对称轴,故C正确;
对于:的图像向右平移个单位得到的图像,故D正确.
故选:.
先根据图象求出的解析式,再分别验证、、、是否正确,根据图象得到的周期进行判定;求得的取值范围,然后利用正弦函数的单调性结合复合函数单调性法则判定;计算,看是否经过顶点从而判定是否为对称轴从而判定;利用“左加右减”求得平移后的函数解析式即可判断.
本题考查了由的部分图象确定其解析式,考查了正弦函数的性质的应用,考查了函数思想,属于中档题.
12.【答案】
【解析】解:对于:,,
,由正弦定理可得,
由余弦定理得,
,,故A正确;
对于:,,
由余弦定理可得,,
,当且仅当,等号成立,
故周长的最小值为,故B正确.
对于:由余弦定理可得,
,,解得或舍去,故C错误;
对于:由正弦定理得,,面积
故D正确;
故选:.
由正弦定理可得,再由余弦定理可得,可求可判断;由面积可得,进而由余弦定理可得,进而可得周长的最小值可判断;由余弦定理可得,可求判断;由正弦定理可求,进而可求面积判断.
本题考查正余弦定理在解三角形中的应用,考查三角形的面积,考查运算求解能力,属中档题.
13.【答案】
【解析】解:由题意,因为::::,
所以女学生中抽取总人数的,
故.
故答案为:.
先求三层的比例,然后求得女学生中抽取总人数的比例,从而求出抽取样本容量.
本题考查了分层抽样方法的应用问题,是基础题.
14.【答案】
【解析】解:.
故答案为:.
根据已知条件,结合三角函数的诱导公式,以及正弦的两角和公式,即可求解.
本题主要考查正弦的两角和公式,属于基础题.
15.【答案】
【解析】解:,
则.
故答案为:.
根据已知条件,结合平面向量的线性运算,以及平面向量的数量积公式,即可求解.
本题主要考查平面向量的线性运算,以及平面向量的数量积公式,属于基础题.
16.【答案】
【解析】解:在中,;
在中,;
,,又,
,
整理,可得,即,
,,
在中,,
,解得舍或,
.
故答案为:.
根据,结合余弦定理,列方程组可求得.
本题考查了余弦定理在解三角形中的应用,考查了转化思想和方程思想,属中档题.
17.【答案】解:由,可得,又,,
则,
又,所以,
;
由,可得,
即,
由可得:,解得.
【解析】由夹角公式及模长计算公式计算即可;
由向量垂直的性质,利用数量积为建立方程,求得值.
本题考查平面向量数量积的运算和性质,考查向量垂直的性质,属基础题.
18.【答案】解:Ⅰ因为,
由正弦定理可得,
所以,
因为为三角形内角,,
所以,
所以;
Ⅱ因为,,,
所以,
由正弦定理,可得,
所以,
.
【解析】Ⅰ由正弦定理,两角和的正弦公式化简已知等式可得,进而可求的值;
Ⅱ由已知利用三角形内角和定理可求的值,进而利用正弦定理即可求解,的值.
本题考查了正弦定理,两角和的正弦公式,三角形内角和定理在解三角形中的综合应用,考查了计算能力和转化思想,属于中档题.
19.【答案】解:成绩落在的频率为,
补全的频率分布直方图,如图所示:
估计这名学生成绩的众数是,
平均数是分,
设分位数为,则,
解得分.
【解析】由频率和为,求出成绩落在的频率;
由频率分布直方图计算样本的众数、平均数和百分位数.
本题考查百分位数等基础知识,考查运算求解能力,是基础题.
20.【答案】解:设,
在地听到弹射声音的时间比地晚秒,
,
在中,由余弦定理,得,
,解得,
故B,两地间的距离为米.
在中,,,
米.
故该仪器的垂直弹射高度为米.
【解析】设,利用在地听到弹射声音的时间比地晚秒,表示出,再由余弦定理,即可得解;
在中,由正切函数的定义,即可得解.
本题考查解三角形的实际应用,熟练掌握余弦定理是解题的关键,考查逻辑推理能力和运算能力,属于基础题.
21.【答案】解:,,,
,
当时,,不合题意,
当时,,
,;
,
,,
,
当时,有最大值,最大值为,
当时,有最小值,最小值为.
【解析】本题考查了向量的平行和向量的数量积以及三角函数的化简和三角函数的性质,属于基础题.
根据向量的平行分和两种情况讨论即可得到,问题得以解决.
根据向量的数量积和两角和余弦公式和余弦函数的性质即可求出.
22.【答案】解:,
,
,
,,
为锐角,
,
,
由正余弦定理可得,
整理可得,
解得.
,
,,
,
,
,
,,,
,
,
,
【解析】利用两角和的正弦公式化简已知等式可得,结合为锐角,可得的值,由正余弦定理化简已知等式即可求解的值.
利用正弦定理,三角函数恒等变换的应用,三角形的面积公式可求,由题意可求范围,利用正弦函数的性质即可求解其范围.
本题主要考查了正弦定理,余弦定理,三角函数恒等变换,三角形的面积公式以及正弦函数的性质在解三角形中的综合应用,考查了转化思想和函数思想,属于中档题.
第1页,共1页
一、单选题(本大题共8小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1. 已知,为虚数单位,则( )
A. B. C. D.
2. 在中,内角,,所对的边为,,,若,,,则( )
A. B. 或 C. D. 或
3. 若一个样本容量为的样本的平均数为,方差为现样本中又加入一个新数据,此时样本容量为,平均数为,方差为,则( )
A. , B. , C. , D. ,
4. 如图,在梯形中,,,设,,则( )
A. B. C. D.
5. 若,,则( )
A. B. C. D.
6. 已知,则( )
A. B.
C. D.
7. 海伦公式是利用三角形的三条边的边长,,直接求三角形面积的公式,表达式为:,;它的特点是形式漂亮,便于记忆.中国宋代的数学家秦九韶在年独立提出了“三斜求积术”,虽然它与海伦公式形式上有所不同,但它与海伦公式完全等价,因此海伦公式又译作海伦秦九韶公式.现在有周长为的满足::::,则用以上给出的公式求得的面积为( )
A. B. C. D.
8. 已知函数, 为的零点,为图象的对称轴,且在上单调,则的最大值为( )
A. B. C. D.
二、多选题(本大题共4小题,共20.0分。在每小题有多项符合题目要求)
9. 复数,是虚数单位,则下列结论正确的是( )
A. B. 的共轭复数为
C. 的实部与虚部之和为 D. 在复平面内的对应点位于第一象限
10. 下列函数中是奇函数,且最小正周期是的函数是( )
A. B.
C. D.
11. 已知函数的部分图象如图所示,下列说法正确的是( )
A. 函数的最小正周期为
B. 函数在单调递减
C. 函数的图象关于直线对称
D. 该图象向右平移个单位可得的图象
12. 三角形的三边,,所对的角为,,,,则下列说法正确的是( )
A.
B. 若面积为,则周长的最小值为
C. 当,时,
D. 若,,则面积为
三、填空题(本大题共4小题,共20.0分)
13. 某校共有师生人,其中教师人,男学生人,女学生人.现用比例分配的分层随机抽样方法从所有师生中抽取一个容量为的样本,已知从女学生中抽取的人数为,那么______.
14. ______ .
15. 在边长为的正中,若点满足,则 ______ .
16. 在中,,,为边上的中点,且的长度为,则 ______ .
四、解答题(本大题共6小题,共70.0分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
设向量满足,,.
求向量,的夹角及;
若,则实数的值.
18. 本小题分
的内角,,的对边分别为,,,已知.
Ⅰ求;
Ⅱ若,,求,的值.
19. 本小题分
年月日,神舟十五号载人飞船返回舱在预定区域成功着陆,航天员费俊龙,邓清明,张陆顺利出舱,神舟十五号载人飞行任务圆满完成为纪念中国航天事业所取得的成就,发扬并传承中国航天精神,某市随机抽取名学生进行了航天知识竞赛并记录得分满分:分,将学生的成绩整理后分成五组,从左到右依次记为,,,,,并绘制成如图所示的频率分布直方图.
请补全频率分布直方图;
估计这名学生成绩的众数、平均数和计算分位数求平均值时同一组数据用该组区间的中点值作代表,分位数小数点后面保留两位有效数字.
20. 本小题分
为了应对日益严重的气候问题,某气象仪器科研单位研究出一种新的“弹射型”气候仪器,这种仪器可以弹射到空中进行气候观测,如图所示,,,三地位于同一水平面上,这种仪器在地进行弹射实验,观测点,两地相距,,在地听到弹射声音的时间比地晚秒,在地测得该仪器至最高点处的仰角为已知声音的传播速度为
求:,两地间的距离;
这种仪器的垂直弹射高度.
21. 本小题分
已知向量,,.
若,求的值;
记,求的最大值和最小值以及对应的的值.
22. 本小题分
在锐角中,角,,的对边分别为,,,若,.
求角的大小和边长的值;
求面积的取值范围.
答案和解析
1.【答案】
【解析】解:因为,即,
由复数相等的定义可得,,即.
故选:.
利用复数相等的定义求解即可.
本题考查了复数相等定义的理解和应用,属于基础题.
2.【答案】
【解析】解:因为,,,
所以由正弦定理有:,
所以,
因为,所以,
所以.
故选:.
由正弦定理可得,再结合大边对大角即可求得.
本题考查正弦定理的应用,属于基础题.
3.【答案】
【解析】解:某个数据的平均数为,方差为,现又加入一个新数据,
此时这个数的平均数为,方差为,
,.
故选:.
利用平均数、方差的定义直接求解.
本题考查平均数、方差的求法,考查推理论证能力、运算求解能力,考查化归与转化思想,是基础题.
4.【答案】
【解析】【分析】
本题主要考查了平面向量的基本运算,属于基础试题.
取中点,由可知,从而可得四边形为平行四边形,结合向量的基本运算即可求解.
【解答】
解:取中点,由可知,
四边形为平行四边形,
则.
故选:.
5.【答案】
【解析】解:因为,,
所以,,
所以.
故选:.
由已知利用同角三角函数基本关系式可求的值,进而利用诱导公式,二倍角的正切函数公式即可计算得解.
本题主要考查了同角三角函数基本关系式,诱导公式,二倍角的正切函数公式在三角函数化简求值中的应用,考查了转化思想,属于基础题.
6.【答案】
【解析】【分析】
利用三角形法则可求得,由向量共线条件可得与共线,从而可得结论.本题考查向量共线的条件,属基础题,熟记向量共线的充要条件是解决问题的关键.
【解答】
解:,
又,所以,则与共线,
又与有公共点,
所以、、三点共线.
故选A.
7.【答案】
【解析】解:::::,::::,
周长为,即,
,,,,
的面积.
故选:.
由正弦定理得三角形三边之比,由周长求出三边,代入公式即可.
本题考查了数学文化,考查了正弦定理、三角形面积公式在解三角形中的应用,考查了计算能力和转化思想,属于基础题.
8.【答案】
【解析】【分析】
本题考查三角函数的图象和性质的综合运用,属于较难题目.
结合为的零点,为图象的对称轴,可得为正奇数,且,结合在上单调,可得的最大值.
【解答】
解:为的零点,为图象的对称轴,
,即,,
即,,即为正奇数,
在上单调,则,
即,解得:,
当时,,,
,,
此时在不单调,不满足题意;
当时,,,
,,
此时在单调,满足题意;
故的最大值为,
故选B.
9.【答案】
【解析】解:,
对于,,故A错误,
对于,的共轭复数为,故B错误,
对于,的实部与虚部之和为,故C正确,
对于,在复平面内的对应点位于第一象限,故D正确.
故选:.
根据已知条件,先对化简,再结合复数模公式,共轭复数的定义,实部和虚部的定义,复数的几何意义,即可求解.
本题主要考查复数模公式,共轭复数的定义,实部和虚部的定义,复数的几何意义,属于基础题.
10.【答案】
【解析】解:对于,函数既是奇函数,函数的最小正周期也为,故A正确;
对于:函数不是周期函数,故B错误;
对于:既是奇函数,函数的最小正周期也为,故C正确;
对于:函数为偶函数,故D错误.
故选:.
直接利用函数的奇偶性和周期性判断结果.
本题考查的知识要点:函数的奇偶性和周期性,主要考查学生的理解能力和计算能力,属于中档题.
11.【答案】
【解析】解:由图象可知:,周期,
;
由,解得:,
故函数.
对于:,故A错误;
对于:当时,因为上正弦函数先减后增,不单调,所以在上不单调,故B错误;
对于:当时,即直线是的一条对称轴,故C正确;
对于:的图像向右平移个单位得到的图像,故D正确.
故选:.
先根据图象求出的解析式,再分别验证、、、是否正确,根据图象得到的周期进行判定;求得的取值范围,然后利用正弦函数的单调性结合复合函数单调性法则判定;计算,看是否经过顶点从而判定是否为对称轴从而判定;利用“左加右减”求得平移后的函数解析式即可判断.
本题考查了由的部分图象确定其解析式,考查了正弦函数的性质的应用,考查了函数思想,属于中档题.
12.【答案】
【解析】解:对于:,,
,由正弦定理可得,
由余弦定理得,
,,故A正确;
对于:,,
由余弦定理可得,,
,当且仅当,等号成立,
故周长的最小值为,故B正确.
对于:由余弦定理可得,
,,解得或舍去,故C错误;
对于:由正弦定理得,,面积
故D正确;
故选:.
由正弦定理可得,再由余弦定理可得,可求可判断;由面积可得,进而由余弦定理可得,进而可得周长的最小值可判断;由余弦定理可得,可求判断;由正弦定理可求,进而可求面积判断.
本题考查正余弦定理在解三角形中的应用,考查三角形的面积,考查运算求解能力,属中档题.
13.【答案】
【解析】解:由题意,因为::::,
所以女学生中抽取总人数的,
故.
故答案为:.
先求三层的比例,然后求得女学生中抽取总人数的比例,从而求出抽取样本容量.
本题考查了分层抽样方法的应用问题,是基础题.
14.【答案】
【解析】解:.
故答案为:.
根据已知条件,结合三角函数的诱导公式,以及正弦的两角和公式,即可求解.
本题主要考查正弦的两角和公式,属于基础题.
15.【答案】
【解析】解:,
则.
故答案为:.
根据已知条件,结合平面向量的线性运算,以及平面向量的数量积公式,即可求解.
本题主要考查平面向量的线性运算,以及平面向量的数量积公式,属于基础题.
16.【答案】
【解析】解:在中,;
在中,;
,,又,
,
整理,可得,即,
,,
在中,,
,解得舍或,
.
故答案为:.
根据,结合余弦定理,列方程组可求得.
本题考查了余弦定理在解三角形中的应用,考查了转化思想和方程思想,属中档题.
17.【答案】解:由,可得,又,,
则,
又,所以,
;
由,可得,
即,
由可得:,解得.
【解析】由夹角公式及模长计算公式计算即可;
由向量垂直的性质,利用数量积为建立方程,求得值.
本题考查平面向量数量积的运算和性质,考查向量垂直的性质,属基础题.
18.【答案】解:Ⅰ因为,
由正弦定理可得,
所以,
因为为三角形内角,,
所以,
所以;
Ⅱ因为,,,
所以,
由正弦定理,可得,
所以,
.
【解析】Ⅰ由正弦定理,两角和的正弦公式化简已知等式可得,进而可求的值;
Ⅱ由已知利用三角形内角和定理可求的值,进而利用正弦定理即可求解,的值.
本题考查了正弦定理,两角和的正弦公式,三角形内角和定理在解三角形中的综合应用,考查了计算能力和转化思想,属于中档题.
19.【答案】解:成绩落在的频率为,
补全的频率分布直方图,如图所示:
估计这名学生成绩的众数是,
平均数是分,
设分位数为,则,
解得分.
【解析】由频率和为,求出成绩落在的频率;
由频率分布直方图计算样本的众数、平均数和百分位数.
本题考查百分位数等基础知识,考查运算求解能力,是基础题.
20.【答案】解:设,
在地听到弹射声音的时间比地晚秒,
,
在中,由余弦定理,得,
,解得,
故B,两地间的距离为米.
在中,,,
米.
故该仪器的垂直弹射高度为米.
【解析】设,利用在地听到弹射声音的时间比地晚秒,表示出,再由余弦定理,即可得解;
在中,由正切函数的定义,即可得解.
本题考查解三角形的实际应用,熟练掌握余弦定理是解题的关键,考查逻辑推理能力和运算能力,属于基础题.
21.【答案】解:,,,
,
当时,,不合题意,
当时,,
,;
,
,,
,
当时,有最大值,最大值为,
当时,有最小值,最小值为.
【解析】本题考查了向量的平行和向量的数量积以及三角函数的化简和三角函数的性质,属于基础题.
根据向量的平行分和两种情况讨论即可得到,问题得以解决.
根据向量的数量积和两角和余弦公式和余弦函数的性质即可求出.
22.【答案】解:,
,
,
,,
为锐角,
,
,
由正余弦定理可得,
整理可得,
解得.
,
,,
,
,
,
,,,
,
,
,
【解析】利用两角和的正弦公式化简已知等式可得,结合为锐角,可得的值,由正余弦定理化简已知等式即可求解的值.
利用正弦定理,三角函数恒等变换的应用,三角形的面积公式可求,由题意可求范围,利用正弦函数的性质即可求解其范围.
本题主要考查了正弦定理,余弦定理,三角函数恒等变换,三角形的面积公式以及正弦函数的性质在解三角形中的综合应用,考查了转化思想和函数思想,属于中档题.
第1页,共1页
同课章节目录
