【核心素养目标】人教A版高中数学 选择性必修一 《3.1.2椭圆的简单几何性质(2)》 教案(含教学反思)
文档属性
| 名称 | 【核心素养目标】人教A版高中数学 选择性必修一 《3.1.2椭圆的简单几何性质(2)》 教案(含教学反思) |

|
|
| 格式 | docx | ||
| 文件大小 | 605.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-26 00:00:00 | ||
图片预览




文档简介
人教A版高中数学选择性必修一
《3.1.2椭圆的简单几何性质(2)》教学设计
【教材分析】
本节课选自《2019人教A版高中数学选择性必修第一册》第二章《直线和圆的方程》,本节课主要学习椭圆的简单几何性质,教材的地位和作用地位:本节课是在椭圆的概念和标准方程的基础上,运用代数的方法,研究椭圆的简单几何性质及简单应用 . 本节课内容的掌握程度直接影响学习双曲线和抛物线几何性质.作用:提高学生的数学素质,培养学生的数形结合思想,及分析问题和解决问题的能力.因此,内容在解析几何中占有非常重要的地位.
【学情分析】
椭圆是高中数学课程内容中较难的一章节,需要学生具备良好的解析几何思维以及综合计算能力,通过学习椭圆,理解其几何意义,掌握其标准方程和几何性质,并会综合应用解决问题,在本节课程学习中,要注重学生对概念的理解,从简单的题目入手,直接应用性质解题,循序渐进,逐步掌握综合应用题目的解题思路和方法.
【教学目标与核心素养】
教学目标:
A.根据几何条件求出椭圆的方程.
B. 进一步掌握椭圆的方程及其性质的应用;
C.会判断直线与椭圆的位置关系.
核心素养:
1.数学抽象:椭圆的几何性质
2.逻辑推理:利用椭圆的方程研究椭圆的几何性
3.数学运算:直线与椭圆位置关系的判断
4.数学建模:利用椭圆的知识解决应用问题
【教学重点】
椭圆的方程及其性质的应用
【教学难点】
直线与椭圆的位置关系
【教学方法】
启发教学法,讲授法
【教学过程】
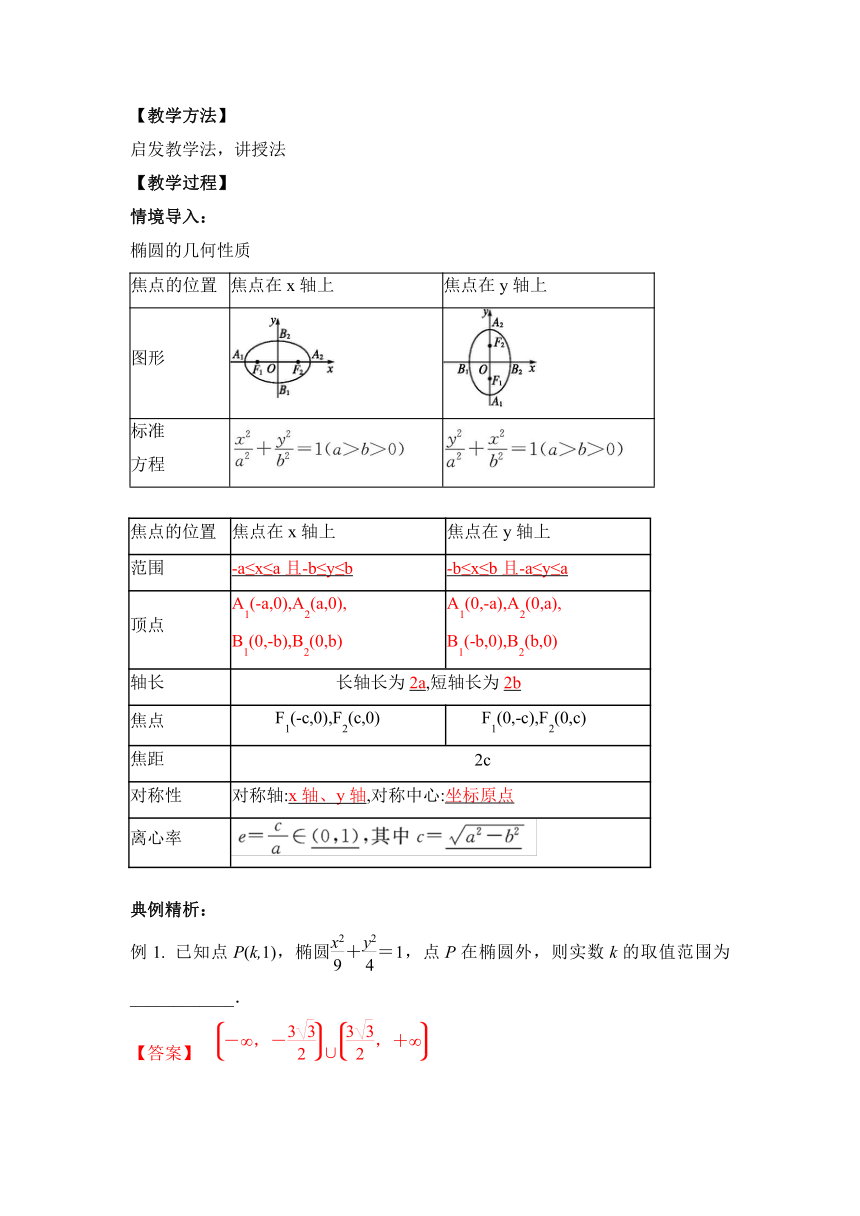
情境导入:
椭圆的几何性质
焦点的位置 焦点在x轴上 焦点在y轴上
图形
标准 方程
焦点的位置 焦点在x轴上 焦点在y轴上
范围 -a≤x≤a且-b≤y≤b -b≤x≤b且-a≤y≤a
顶点 A1(-a,0),A2(a,0), B1(0,-b),B2(0,b) A1(0,-a),A2(0,a), B1(-b,0),B2(b,0)
轴长 长轴长为2a,短轴长为2b
焦点 F1(-c,0),F2(c,0) F1(0,-c),F2(0,c)
焦距 2c
对称性 对称轴:x轴、y轴,对称中心:坐标原点
离心率
典例精析:
例1. 已知点P(k,1),椭圆+=1,点P在椭圆外,则实数k的取值范围为____________.
【答案】 ∪
【解析】 依题意得,+>1,解得k<-或k>.
课堂练习:
跟踪训练1.已知点(1,2)在椭圆+=1(n>m>0)上,则m+n的最小值为________.
【答案】 9
【解析】 依题意得,+=1,而m+n=(m+n)=1+++4=5++≥5+2=9,当且仅当n=2m时等号成立,故m+n的最小值为9.
典例精析:
例2. 已知直线l:y=2x+m,椭圆C:+=1.试问当m取何值时,直线l与椭圆C:
(1)有两个公共点;
(2)有且只有一个公共点;
(3)没有公共点.
[思路探究] →
→→得出结论
[解] 直线l的方程与椭圆C的方程联立,得方程组消去y,
得9x2+8mx+2m2-4=0 ①.
方程①的判别式Δ=(8m)2-4×9×(2m2-4)=-8m2+144.
(1)当Δ>0,即-3<m<3时,方程①有两个不同的实数根,可知原方程组有两组不同的实数解.这时直线l与椭圆C有两个公共点.
(2)当Δ=0,即m=±3时,方程①有两个相同的实数解,可知原方程组有两组相同的实数解.这时直线l与椭圆C有且只有一个公共点.
(3)当Δ<0,即m<-3或m>3时,方程①没有实数解,可知原方程组没有实数解.这时直线l与椭圆C没有公共点.
归纳总结:
代数法判断直线与椭圆的位置关系
判断直线与椭圆的位置关系,通过解直线方程与椭圆方程组成的方程组,消去方程组中的一个变量,得到关于另一个变量的一元二次方程,则
Δ>0 直线与椭圆相交;
Δ=0 直线与椭圆相切;
Δ<0 直线与椭圆相离.
提醒:注意方程组的解与交点个数之间的等价关系.
课堂练习:
跟踪训练2.若直线y=kx+1(k∈R)与椭圆+=1恒有公共点,求实数m的取值范围.
[解] 因为y=kx+1(k∈R)恒过点(0,1),则点(0,1)在椭圆+=1内或椭圆上时,直线与椭圆恒有公共点,所以≤1,即m≥1.
当m=5时,+=1不是椭圆,它是以原点为圆心,半径为的圆.
因此,m的取值范围为[1,5)∪(5,+∞).
典例精析:
例3. 已知椭圆及直线:
(1)当直线与该椭圆有公共点时,求实数的取值范围;
(2)当时,求直线被椭圆截得的弦长.
【答案】(1);(2).
【解析】(1)由消去,
并整理得……①
∵直线与椭圆有公共点
∴,可解得:
故所求实数的取值范围为.
(2)设直线与椭圆的交点为,
由①得: ,
当时,直线被椭圆截得的弦长为.
课堂练习:
跟踪训练3.斜率为1的直线与椭圆相交于两点,则的最大值为_____.
【答案】
【解析】
斜率是1的直线L:y=x+b代入,化简得,
设,则,
且,解得.
,
∴b=0时,|AB|的最大值为,故答案为:.
典例精析:
例4.(1)直线与圆相交于两点,,弦的中点为,则直线的方程为__________.
已知椭圆E:,的右焦点为,过点F的直线交椭圆E于A、B两点.若AB的中点坐标为,则E的方程为__________.
(3)直线y=x+1与椭圆mx2+ny2=1(m>n>0)相交于A,B两点,若弦AB的中点的横坐标等于,则椭圆的离心率等于_________.
【答案】(1).(2)(3)
【解析】(1)设圆心,直线的斜率为,弦AB的中点为,的斜率为,则,所以
由点斜式得.
(2)已知,设,,则①,②,
已知AB的中点坐标为,,
①-②得,
∴,
∵,∴,即,
又,
∴,,即E的方程为.
(3)设A(x1,y1),B(x2,y2),AB的中点为M(x0,y0),x0=-,代入y=x+1得y0=.
所以m x12+n y12=1,(1)m x22+n y22=1,(2)
由(1)-(2)得:,
,∴,
∴e2,∴e=.故答案为:.
课堂练习:
跟踪训练4.如果椭圆的弦被点(4,2)平分,则这条弦所在的直线方程是________.
【答案】 y=-0.5x+4
【解析】设弦为,且,代入椭圆方程得
,两式作差并化简得,即弦的斜率为,由点斜式得,化简得.
达标检测:
1.已知椭圆+=1(a>b>0)与椭圆+=1有相同的长轴,
椭圆+=1(a>b>0)的短轴长与+=1的短轴长相等,则( )
A.a2=15,b2=16 B.a2=9,b2=25
C.a2=25,b2=9或a2=9,b2=25 D.a2=25,b2=9
【答案】D
[由题意得,椭圆+=1的焦点在x轴上,且a2=25,b2=9.]
2.若点P(a,1)在椭圆+=1的外部,则a的取值范围为( )
A. B.∪
C. D.
B [由题意知+>1,即a2>,解得a>或a<-.]
3.(2018·全国高考)已知椭圆:的一个焦点为,则的离心率为( )
A. B. C. D.
【答案】C
【解析】根据题意,可知,因为,所以,
即,所以椭圆的离心率为,故选C.
4.(2019·全国高考)已知椭圆C的焦点为,过F2的直线与C交于A,B两点.若,,则C的方程为
A. B.
C. D.
【答案】B
【解析】法一:如图,由已知可设,则,由椭圆的定义有.在中,
由余弦定理推论得.在中,由余弦定理得,解得.
所求椭圆方程为,故选B.
法二:由已知可设,则,由椭圆的定义有.在和中,由余弦定理得,又互补,,
两式消去,得,解得
所求椭圆方程为,故选B.
5.椭圆x2+4y2=16被直线y=x+1截得的弦长为________.
[由
消去y并化简得x2+2x-6=0.
设直线与椭圆的交点为M(x1,y1),N(x2,y2),
则x1+x2=-2,x1x2=-6.
∴弦长|MN|=|x1-x2|===.]
6.设椭圆C:+=1(a>b>0)过点(0,4),离心率为.
(1)求椭圆C的方程;
(2)求过点(3,0)且斜率为的直线被C所截线段的中点的坐标.
[解] (1)将(0,4)代入C的方程,得=1,∴b=4.
由e==,得=,即1-=,∴a=5,
∴椭圆C的方程为+=1.
(2)过点(3,0)且斜率为的直线方程为y=(x-3).
设直线与C的交点为A(x1,y1),B(x2,y2),
将直线AB的方程y=(x-3)代入C的方程,
得+=1,即x2-3x-8=0,
则x1+x2=3,∴=,=(x1+x2-6)=-,
即中点的坐标为.
【课后小结】
【板书设计】
【教学反思】
通过对椭圆几何性质的应用,培养学生数学建模能力,并向学生介绍椭圆的定义二定义,体会圆锥曲线的统一性.在直线与椭圆学习过程中,注意类比直线与圆的位置关系的判断方法.
《3.1.2椭圆的简单几何性质(2)》教学设计
【教材分析】
本节课选自《2019人教A版高中数学选择性必修第一册》第二章《直线和圆的方程》,本节课主要学习椭圆的简单几何性质,教材的地位和作用地位:本节课是在椭圆的概念和标准方程的基础上,运用代数的方法,研究椭圆的简单几何性质及简单应用 . 本节课内容的掌握程度直接影响学习双曲线和抛物线几何性质.作用:提高学生的数学素质,培养学生的数形结合思想,及分析问题和解决问题的能力.因此,内容在解析几何中占有非常重要的地位.
【学情分析】
椭圆是高中数学课程内容中较难的一章节,需要学生具备良好的解析几何思维以及综合计算能力,通过学习椭圆,理解其几何意义,掌握其标准方程和几何性质,并会综合应用解决问题,在本节课程学习中,要注重学生对概念的理解,从简单的题目入手,直接应用性质解题,循序渐进,逐步掌握综合应用题目的解题思路和方法.
【教学目标与核心素养】
教学目标:
A.根据几何条件求出椭圆的方程.
B. 进一步掌握椭圆的方程及其性质的应用;
C.会判断直线与椭圆的位置关系.
核心素养:
1.数学抽象:椭圆的几何性质
2.逻辑推理:利用椭圆的方程研究椭圆的几何性
3.数学运算:直线与椭圆位置关系的判断
4.数学建模:利用椭圆的知识解决应用问题
【教学重点】
椭圆的方程及其性质的应用
【教学难点】
直线与椭圆的位置关系
【教学方法】
启发教学法,讲授法
【教学过程】
情境导入:
椭圆的几何性质
焦点的位置 焦点在x轴上 焦点在y轴上
图形
标准 方程
焦点的位置 焦点在x轴上 焦点在y轴上
范围 -a≤x≤a且-b≤y≤b -b≤x≤b且-a≤y≤a
顶点 A1(-a,0),A2(a,0), B1(0,-b),B2(0,b) A1(0,-a),A2(0,a), B1(-b,0),B2(b,0)
轴长 长轴长为2a,短轴长为2b
焦点 F1(-c,0),F2(c,0) F1(0,-c),F2(0,c)
焦距 2c
对称性 对称轴:x轴、y轴,对称中心:坐标原点
离心率
典例精析:
例1. 已知点P(k,1),椭圆+=1,点P在椭圆外,则实数k的取值范围为____________.
【答案】 ∪
【解析】 依题意得,+>1,解得k<-或k>.
课堂练习:
跟踪训练1.已知点(1,2)在椭圆+=1(n>m>0)上,则m+n的最小值为________.
【答案】 9
【解析】 依题意得,+=1,而m+n=(m+n)=1+++4=5++≥5+2=9,当且仅当n=2m时等号成立,故m+n的最小值为9.
典例精析:
例2. 已知直线l:y=2x+m,椭圆C:+=1.试问当m取何值时,直线l与椭圆C:
(1)有两个公共点;
(2)有且只有一个公共点;
(3)没有公共点.
[思路探究] →
→→得出结论
[解] 直线l的方程与椭圆C的方程联立,得方程组消去y,
得9x2+8mx+2m2-4=0 ①.
方程①的判别式Δ=(8m)2-4×9×(2m2-4)=-8m2+144.
(1)当Δ>0,即-3<m<3时,方程①有两个不同的实数根,可知原方程组有两组不同的实数解.这时直线l与椭圆C有两个公共点.
(2)当Δ=0,即m=±3时,方程①有两个相同的实数解,可知原方程组有两组相同的实数解.这时直线l与椭圆C有且只有一个公共点.
(3)当Δ<0,即m<-3或m>3时,方程①没有实数解,可知原方程组没有实数解.这时直线l与椭圆C没有公共点.
归纳总结:
代数法判断直线与椭圆的位置关系
判断直线与椭圆的位置关系,通过解直线方程与椭圆方程组成的方程组,消去方程组中的一个变量,得到关于另一个变量的一元二次方程,则
Δ>0 直线与椭圆相交;
Δ=0 直线与椭圆相切;
Δ<0 直线与椭圆相离.
提醒:注意方程组的解与交点个数之间的等价关系.
课堂练习:
跟踪训练2.若直线y=kx+1(k∈R)与椭圆+=1恒有公共点,求实数m的取值范围.
[解] 因为y=kx+1(k∈R)恒过点(0,1),则点(0,1)在椭圆+=1内或椭圆上时,直线与椭圆恒有公共点,所以≤1,即m≥1.
当m=5时,+=1不是椭圆,它是以原点为圆心,半径为的圆.
因此,m的取值范围为[1,5)∪(5,+∞).
典例精析:
例3. 已知椭圆及直线:
(1)当直线与该椭圆有公共点时,求实数的取值范围;
(2)当时,求直线被椭圆截得的弦长.
【答案】(1);(2).
【解析】(1)由消去,
并整理得……①
∵直线与椭圆有公共点
∴,可解得:
故所求实数的取值范围为.
(2)设直线与椭圆的交点为,
由①得: ,
当时,直线被椭圆截得的弦长为.
课堂练习:
跟踪训练3.斜率为1的直线与椭圆相交于两点,则的最大值为_____.
【答案】
【解析】
斜率是1的直线L:y=x+b代入,化简得,
设,则,
且,解得.
,
∴b=0时,|AB|的最大值为,故答案为:.
典例精析:
例4.(1)直线与圆相交于两点,,弦的中点为,则直线的方程为__________.
已知椭圆E:,的右焦点为,过点F的直线交椭圆E于A、B两点.若AB的中点坐标为,则E的方程为__________.
(3)直线y=x+1与椭圆mx2+ny2=1(m>n>0)相交于A,B两点,若弦AB的中点的横坐标等于,则椭圆的离心率等于_________.
【答案】(1).(2)(3)
【解析】(1)设圆心,直线的斜率为,弦AB的中点为,的斜率为,则,所以
由点斜式得.
(2)已知,设,,则①,②,
已知AB的中点坐标为,,
①-②得,
∴,
∵,∴,即,
又,
∴,,即E的方程为.
(3)设A(x1,y1),B(x2,y2),AB的中点为M(x0,y0),x0=-,代入y=x+1得y0=.
所以m x12+n y12=1,(1)m x22+n y22=1,(2)
由(1)-(2)得:,
,∴,
∴e2,∴e=.故答案为:.
课堂练习:
跟踪训练4.如果椭圆的弦被点(4,2)平分,则这条弦所在的直线方程是________.
【答案】 y=-0.5x+4
【解析】设弦为,且,代入椭圆方程得
,两式作差并化简得,即弦的斜率为,由点斜式得,化简得.
达标检测:
1.已知椭圆+=1(a>b>0)与椭圆+=1有相同的长轴,
椭圆+=1(a>b>0)的短轴长与+=1的短轴长相等,则( )
A.a2=15,b2=16 B.a2=9,b2=25
C.a2=25,b2=9或a2=9,b2=25 D.a2=25,b2=9
【答案】D
[由题意得,椭圆+=1的焦点在x轴上,且a2=25,b2=9.]
2.若点P(a,1)在椭圆+=1的外部,则a的取值范围为( )
A. B.∪
C. D.
B [由题意知+>1,即a2>,解得a>或a<-.]
3.(2018·全国高考)已知椭圆:的一个焦点为,则的离心率为( )
A. B. C. D.
【答案】C
【解析】根据题意,可知,因为,所以,
即,所以椭圆的离心率为,故选C.
4.(2019·全国高考)已知椭圆C的焦点为,过F2的直线与C交于A,B两点.若,,则C的方程为
A. B.
C. D.
【答案】B
【解析】法一:如图,由已知可设,则,由椭圆的定义有.在中,
由余弦定理推论得.在中,由余弦定理得,解得.
所求椭圆方程为,故选B.
法二:由已知可设,则,由椭圆的定义有.在和中,由余弦定理得,又互补,,
两式消去,得,解得
所求椭圆方程为,故选B.
5.椭圆x2+4y2=16被直线y=x+1截得的弦长为________.
[由
消去y并化简得x2+2x-6=0.
设直线与椭圆的交点为M(x1,y1),N(x2,y2),
则x1+x2=-2,x1x2=-6.
∴弦长|MN|=|x1-x2|===.]
6.设椭圆C:+=1(a>b>0)过点(0,4),离心率为.
(1)求椭圆C的方程;
(2)求过点(3,0)且斜率为的直线被C所截线段的中点的坐标.
[解] (1)将(0,4)代入C的方程,得=1,∴b=4.
由e==,得=,即1-=,∴a=5,
∴椭圆C的方程为+=1.
(2)过点(3,0)且斜率为的直线方程为y=(x-3).
设直线与C的交点为A(x1,y1),B(x2,y2),
将直线AB的方程y=(x-3)代入C的方程,
得+=1,即x2-3x-8=0,
则x1+x2=3,∴=,=(x1+x2-6)=-,
即中点的坐标为.
【课后小结】
【板书设计】
【教学反思】
通过对椭圆几何性质的应用,培养学生数学建模能力,并向学生介绍椭圆的定义二定义,体会圆锥曲线的统一性.在直线与椭圆学习过程中,注意类比直线与圆的位置关系的判断方法.
