3.1.2椭圆的简单几何性质(2) 课件(共29张PPT)
文档属性
| 名称 | 3.1.2椭圆的简单几何性质(2) 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-26 09:38:54 | ||
图片预览








文档简介
(共29张PPT)
人教A版数学选择性必修第一册
3.1.2椭圆的简单几何性质(2)
1.根据几何条件求出椭圆的方程;
2.进一步掌握椭圆的方程及其性质的应用;
3.会判断直线与椭圆的位置关系.
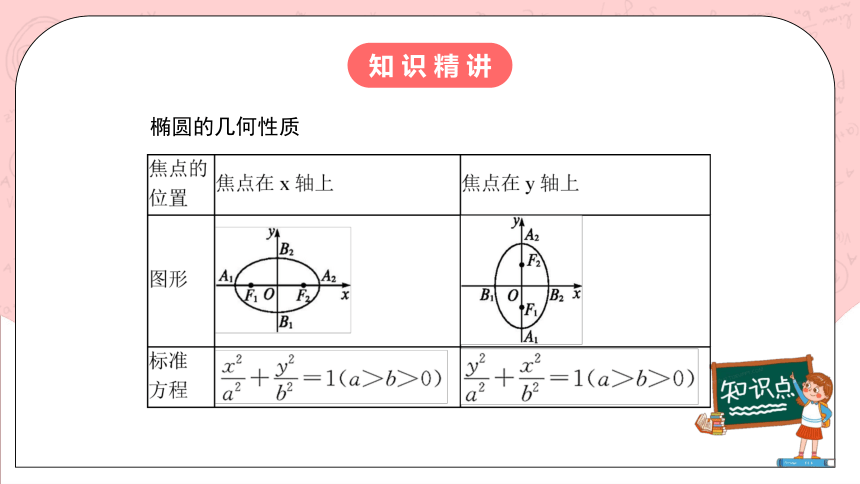
椭圆的几何性质
焦点的位置 焦点在x轴上 焦点在y轴上
范围 -a≤x≤a且-b≤y≤b -b≤x≤b且-a≤y≤a
顶点 A1(-a,0),A2(a,0), B1(0,-b),B2(0,b) A1(0,-a),A2(0,a),
B1(-b,0),B2(b,0)
轴长 长轴长为2a,短轴长为2b 焦点 F1(-c,0),F2(c,0) F1(0,-c),F2(0,c)
焦距 2c 对称性 对称轴:x轴、y轴,对称中心:坐标原点 离心率 例3. 已知椭圆及直线:.
(1)当直线与该椭圆有公共点时,求实数的取值范围;
(2)当时,求直线被椭圆截得的弦长.
【解析】(1)由 消去,并整理得……①
∵直线与椭圆有公共点,∴,可解得:
故所求实数的取值范围为.
(2)设直线与椭圆的交点为,
由①得: ,
当时,直线被椭圆截得的弦长为.
跟踪训练3.斜率为1的直线与椭圆相交于两点,则的最大值为_____.
【解析】斜率是1的直线L:y=x+b代入,化简得,
设,则,
且,解得.
,
∴b=0时,|AB|的最大值为,故答案为:.
例4.(1)直线与圆相交于两点,,弦的中点为,则直线的方程为__________.
【答案】(1).(2)(3)
【解析】(1)设圆心,直线的斜率为,弦AB的中点为,的斜率为,则,所以
由点斜式得.
(2)已知椭圆E:,的右焦点为,过点F的直线交椭圆E于A、B两点.若AB的中点坐标为,则E的方程为__________.
【解析】已知,设,,则①,②,
已知AB的中点坐标为,,
①-②得,∴,
∵,∴,即,又,
∴,,即E的方程为.
(3)直线y=x+1与椭圆mx2+ny2=1(m>n>0)相交于A,B两点,若弦AB的中点的横坐标等于,则椭圆的离心率等于_________.
【解析】设A(x1,y1),B(x2,y2),AB的中点为M(x0,y0),x0=-,代入y=x+1得y0=.
所以m x12+n y12=1,(1)m x22+n y22=1,(2)
由(1)-(2)得:,
,∴,∴e2,∴e=.
故答案为:.
跟踪训练4.如果椭圆的弦被点(4,2)平分,则这条弦所在的直线方程是________.
【答案】 y=-0.5x+4
【解析】设弦为,且,代入椭圆方程得
,两式作差并化简得,
即弦的斜率为,由点斜式得,化简得.
3.(2018·全国高考)已知椭圆:的一个焦点为,则的离心率为( )
A. B. C. D.
【答案】C
【解析】根据题意,可知,因为,所以,
即,所以椭圆的离心率为,故选C.
4.(2019·全国高考)已知椭圆C的焦点为,过F2的直线与C交于A,B两点.若,,则C的方程为( )
A. B.
C. D.
【答案】B
【解析】法一:如图,由已知可设,
则,由椭圆的定义有
.在中,
由余弦定理推论得.在中,
由余弦定理得,解得.
所求椭圆方程为,故选B.
法二:由已知可设,则,
由椭圆的定义有.
在和中,由余弦定理得,
又互补,,
两式消去,得,解得.
所求椭圆方程为,故选B.
课程结束
人教A版数学选择性必修第一册
3.1.2椭圆的简单几何性质(2)
1.根据几何条件求出椭圆的方程;
2.进一步掌握椭圆的方程及其性质的应用;
3.会判断直线与椭圆的位置关系.
椭圆的几何性质
焦点的位置 焦点在x轴上 焦点在y轴上
范围 -a≤x≤a且-b≤y≤b -b≤x≤b且-a≤y≤a
顶点 A1(-a,0),A2(a,0), B1(0,-b),B2(0,b) A1(0,-a),A2(0,a),
B1(-b,0),B2(b,0)
轴长 长轴长为2a,短轴长为2b 焦点 F1(-c,0),F2(c,0) F1(0,-c),F2(0,c)
焦距 2c 对称性 对称轴:x轴、y轴,对称中心:坐标原点 离心率 例3. 已知椭圆及直线:.
(1)当直线与该椭圆有公共点时,求实数的取值范围;
(2)当时,求直线被椭圆截得的弦长.
【解析】(1)由 消去,并整理得……①
∵直线与椭圆有公共点,∴,可解得:
故所求实数的取值范围为.
(2)设直线与椭圆的交点为,
由①得: ,
当时,直线被椭圆截得的弦长为.
跟踪训练3.斜率为1的直线与椭圆相交于两点,则的最大值为_____.
【解析】斜率是1的直线L:y=x+b代入,化简得,
设,则,
且,解得.
,
∴b=0时,|AB|的最大值为,故答案为:.
例4.(1)直线与圆相交于两点,,弦的中点为,则直线的方程为__________.
【答案】(1).(2)(3)
【解析】(1)设圆心,直线的斜率为,弦AB的中点为,的斜率为,则,所以
由点斜式得.
(2)已知椭圆E:,的右焦点为,过点F的直线交椭圆E于A、B两点.若AB的中点坐标为,则E的方程为__________.
【解析】已知,设,,则①,②,
已知AB的中点坐标为,,
①-②得,∴,
∵,∴,即,又,
∴,,即E的方程为.
(3)直线y=x+1与椭圆mx2+ny2=1(m>n>0)相交于A,B两点,若弦AB的中点的横坐标等于,则椭圆的离心率等于_________.
【解析】设A(x1,y1),B(x2,y2),AB的中点为M(x0,y0),x0=-,代入y=x+1得y0=.
所以m x12+n y12=1,(1)m x22+n y22=1,(2)
由(1)-(2)得:,
,∴,∴e2,∴e=.
故答案为:.
跟踪训练4.如果椭圆的弦被点(4,2)平分,则这条弦所在的直线方程是________.
【答案】 y=-0.5x+4
【解析】设弦为,且,代入椭圆方程得
,两式作差并化简得,
即弦的斜率为,由点斜式得,化简得.
3.(2018·全国高考)已知椭圆:的一个焦点为,则的离心率为( )
A. B. C. D.
【答案】C
【解析】根据题意,可知,因为,所以,
即,所以椭圆的离心率为,故选C.
4.(2019·全国高考)已知椭圆C的焦点为,过F2的直线与C交于A,B两点.若,,则C的方程为( )
A. B.
C. D.
【答案】B
【解析】法一:如图,由已知可设,
则,由椭圆的定义有
.在中,
由余弦定理推论得.在中,
由余弦定理得,解得.
所求椭圆方程为,故选B.
法二:由已知可设,则,
由椭圆的定义有.
在和中,由余弦定理得,
又互补,,
两式消去,得,解得.
所求椭圆方程为,故选B.
课程结束
