2022-2023学年沪教版数学八年级上册19.6 轨迹课件(共29张PPT)
文档属性
| 名称 | 2022-2023学年沪教版数学八年级上册19.6 轨迹课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-24 00:00:00 | ||
图片预览






文档简介
(共29张PPT)
19.6 轨迹
教学目标
1、 了解轨迹的意义,知道“线段的垂直平分线”,“角的平分线”和“圆”三条基本轨迹;
2、 会用三条基本轨迹解释简单的轨迹问题并用图形语言表示;
3、 通过轨迹的学习,初步感知集合的思想,体会用运动变化的观点,提高探索、归纳、概括新知识的能力.
教学难点
教学重点:用数学语言归纳出三条基本轨迹,并用于解释简单的轨迹问题.
教学难点:轨迹上的任意一点都符合“某些条件”和凡是符合“某些条件”的点都在轨迹上
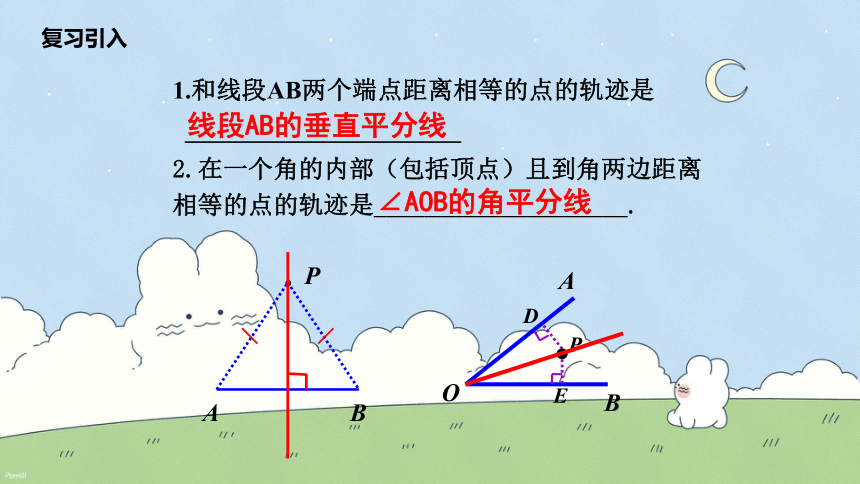
1.和线段AB两个端点距离相等的点的轨迹是
______________________
线段AB的垂直平分线
A
B
P
2.在一个角的内部(包括顶点)且到角两边距离
相等的点的轨迹是____________________.
∠AOB的角平分线
O
A
B
P
E
D
复习引入
3.到定点的距离等于定长的点的轨迹是
____________________________________________________________
1.和线段AB两个端点距离相等的点的轨迹是
______________________
线段AB的垂直平分线
2.在一个角的内部(包括顶点)且到角两边距离
相等的点的轨迹是____________________.
∠AOB的角平分线
以这个定点为圆心、定长为半径的圆
运动的路线给我们以点的轨迹的形象
探究新知
●
●
A
B
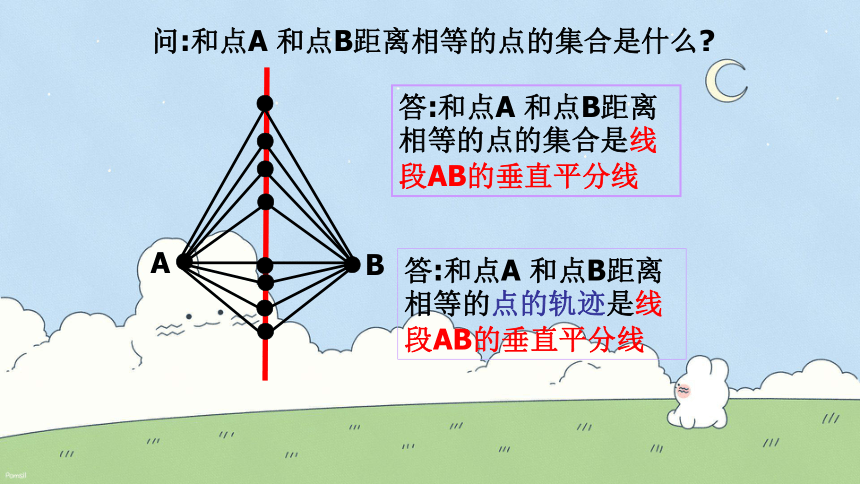
问:和点A 和点B距离相等的点的集合是什么
●
●
●
●
●
●
●
●
答:和点A 和点B距离相等的点的集合是线段AB的垂直平分线
答:和点A 和点B距离相等的点的轨迹是线段AB的垂直平分线
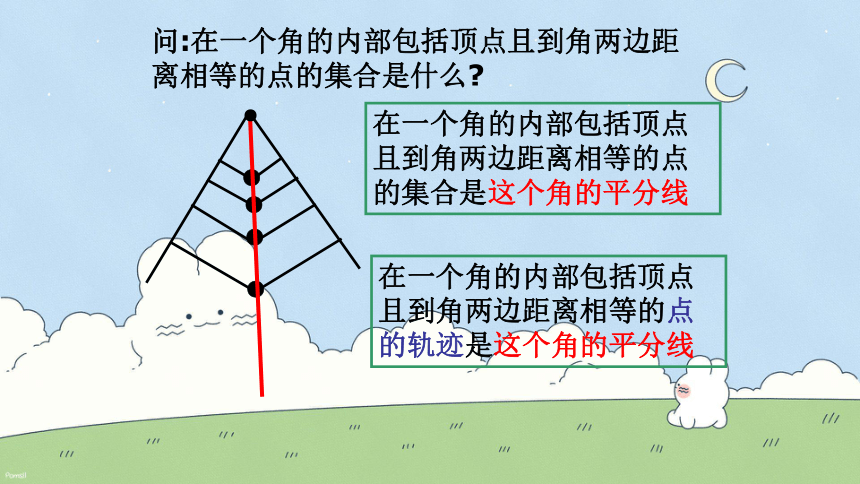
问:在一个角的内部包括顶点且到角两边距离相等的点的集合是什么
●
●
●
●
●
在一个角的内部包括顶点且到角两边距离相等的点的集合是这个角的平分线
在一个角的内部包括顶点且到角两边距离相等的点的轨迹是这个角的平分线
符合某些条件的所有点的集合叫做点的轨迹.
P109
典例精析
例题1 作图并说明符合下列条件的点的轨迹(不要求证明)
⑴底边为AB的等腰三角形的顶角顶点的轨迹.
例题1 作图并说明符合下列条件的点的轨迹(不要求证明)
⑴底边为AB的等腰三角形的顶角顶点的轨迹.
例题1 作图并说明符合下列条件的点的轨迹(不要求证明)
⑴底边为AB的等腰三角形的顶角顶点的轨迹.
轨迹是线段AB的垂直平分线(线段AB的中点除外)
⑵经过定点A且半径为3厘米的圆的圆心的轨迹.
轨迹是以点A为圆心,3厘米长为半径的圆.
⑶已知两个定点A、B的距离为4厘米,这时到点
A、B的距离之和为4厘米的点的轨迹.
轨迹是线段AB
⑷与已知直线CD的距离为3厘米的点的轨迹.
轨迹是平行于直线CD且和CD距离为3厘米的两条直线
例题2 已知:∠AOB和∠AOB内一点C.
求作:点P,使PC=PO,
且点P到∠AOB的两边OA、OB的距离相等.
作法:
1.联结OC,
作线段OC的垂直平分线.
点P在∠AOB的平分线上
2.作∠AOB的平分线,
3.∠AOB的平分线与OC的
垂直平分线相交于点P,
P
∴点P就是所求作的点.
利用轨迹相交进行作图的方法
叫做交轨法.
巩固练习
1.作图并说明符合下列条件的点的轨迹
以线段AB为腰的等腰三角形的顶点C的轨迹;
分别以A、B为圆心,以AB为半径的两个圆
(除与直线AB的交点外).
以AB为对角线的正方形的另一条对角线
(除端点及AB中点外)
2.作图并说明符合下列条件的点的轨迹
以线段AB为底边的等腰三角形的两底角平分线交点D的轨迹;
3.作图并说明符合下列条件的点的轨迹.
和△ABM面积相等的△BCM的顶点M的轨迹.
利用轨迹相交进行作图的方法叫做交轨法.
步骤:
①先找出符合一部分作图要求的点的轨迹;
②再找出符合另一部分作图要求的点的轨迹;
③然后得出这两个轨迹的交点.
练习1 如图,已知∠AOB及点E、F,求作点P,
使点P到OA、OB的距离相等,且PE=PF.
A
E
O
B
F
P
牛刀小试
∴点P就是所求作的点.
作法:
2.联结EF,作线段EF
的垂直平分线
1.作∠AOB的平分线.
3.线段EF的垂直平分线
与∠AOB的平分线交于
点P.
练习2 如图,已知∠MON及线段a,点G在OM上,
作点P,使点P到OM、ON的距离相等,且PG=a.
a
O
M
N
G
P1
P2
∴点P1,P2就是所求作的点.
牛刀小试
作法:
2.以点G为圆心,
a为半径作圆
1.作∠MON的平分线.
3.∠MON的平分线与圆
交于点P1,P2.
问1:画一个三角形关键是确定其三个顶点,
本题中可先确定哪些顶点?
例题4 已知线段 a、h,求作等腰三角形,使其底边长
为a,底边上的高为h.
例题讲解
可先确定等腰三角形的底边的两个端点,
设为BC,BC=a.
问2:顶点A满足什么条件?
AB=AC.
说明点A在线段BC的垂直平分线上,
问3:底边上的高为h?
说明AD=h
∴△ABC就是所
求作的三角形.
例题讲解
例题5 要在某天然气管道MN上修建一个泵站,
分别向A、B两镇供气,泵站修在管道的什么地方,
可使所用的输气管线最短?
B
N
A
M
P
联结线段AB,
交直线MN于点P.
作法:
∴点P就是所求作的点.
P
两点之间线段最短.
理由:
PA+PB最小?
例题讲解
变式 要在某天然气管道MN上修建一个泵站,
分别向A、B两镇供气,泵站修在管道的什么地方,
可使所用的输气管线最短?
B
N
M
A
作法:
1.作点A关于MN的对称点A’.
A’
P
PA+PB最小?
PA'+PB最小?
√
√
P
2.联结A’B,与MN交于点P.
∴点P就是所求作的点.
利用轨迹相交进行作图的方法叫做交轨法.
步骤:
①先找出符合一部分作图要求的点的轨迹;
②再找出符合另一部分作图要求的点的轨迹;
③然后得出这两个轨迹的交点.
作图时,保留作图痕迹
归纳
再见
19.6 轨迹
教学目标
1、 了解轨迹的意义,知道“线段的垂直平分线”,“角的平分线”和“圆”三条基本轨迹;
2、 会用三条基本轨迹解释简单的轨迹问题并用图形语言表示;
3、 通过轨迹的学习,初步感知集合的思想,体会用运动变化的观点,提高探索、归纳、概括新知识的能力.
教学难点
教学重点:用数学语言归纳出三条基本轨迹,并用于解释简单的轨迹问题.
教学难点:轨迹上的任意一点都符合“某些条件”和凡是符合“某些条件”的点都在轨迹上
1.和线段AB两个端点距离相等的点的轨迹是
______________________
线段AB的垂直平分线
A
B
P
2.在一个角的内部(包括顶点)且到角两边距离
相等的点的轨迹是____________________.
∠AOB的角平分线
O
A
B
P
E
D
复习引入
3.到定点的距离等于定长的点的轨迹是
____________________________________________________________
1.和线段AB两个端点距离相等的点的轨迹是
______________________
线段AB的垂直平分线
2.在一个角的内部(包括顶点)且到角两边距离
相等的点的轨迹是____________________.
∠AOB的角平分线
以这个定点为圆心、定长为半径的圆
运动的路线给我们以点的轨迹的形象
探究新知
●
●
A
B
问:和点A 和点B距离相等的点的集合是什么
●
●
●
●
●
●
●
●
答:和点A 和点B距离相等的点的集合是线段AB的垂直平分线
答:和点A 和点B距离相等的点的轨迹是线段AB的垂直平分线
问:在一个角的内部包括顶点且到角两边距离相等的点的集合是什么
●
●
●
●
●
在一个角的内部包括顶点且到角两边距离相等的点的集合是这个角的平分线
在一个角的内部包括顶点且到角两边距离相等的点的轨迹是这个角的平分线
符合某些条件的所有点的集合叫做点的轨迹.
P109
典例精析
例题1 作图并说明符合下列条件的点的轨迹(不要求证明)
⑴底边为AB的等腰三角形的顶角顶点的轨迹.
例题1 作图并说明符合下列条件的点的轨迹(不要求证明)
⑴底边为AB的等腰三角形的顶角顶点的轨迹.
例题1 作图并说明符合下列条件的点的轨迹(不要求证明)
⑴底边为AB的等腰三角形的顶角顶点的轨迹.
轨迹是线段AB的垂直平分线(线段AB的中点除外)
⑵经过定点A且半径为3厘米的圆的圆心的轨迹.
轨迹是以点A为圆心,3厘米长为半径的圆.
⑶已知两个定点A、B的距离为4厘米,这时到点
A、B的距离之和为4厘米的点的轨迹.
轨迹是线段AB
⑷与已知直线CD的距离为3厘米的点的轨迹.
轨迹是平行于直线CD且和CD距离为3厘米的两条直线
例题2 已知:∠AOB和∠AOB内一点C.
求作:点P,使PC=PO,
且点P到∠AOB的两边OA、OB的距离相等.
作法:
1.联结OC,
作线段OC的垂直平分线.
点P在∠AOB的平分线上
2.作∠AOB的平分线,
3.∠AOB的平分线与OC的
垂直平分线相交于点P,
P
∴点P就是所求作的点.
利用轨迹相交进行作图的方法
叫做交轨法.
巩固练习
1.作图并说明符合下列条件的点的轨迹
以线段AB为腰的等腰三角形的顶点C的轨迹;
分别以A、B为圆心,以AB为半径的两个圆
(除与直线AB的交点外).
以AB为对角线的正方形的另一条对角线
(除端点及AB中点外)
2.作图并说明符合下列条件的点的轨迹
以线段AB为底边的等腰三角形的两底角平分线交点D的轨迹;
3.作图并说明符合下列条件的点的轨迹.
和△ABM面积相等的△BCM的顶点M的轨迹.
利用轨迹相交进行作图的方法叫做交轨法.
步骤:
①先找出符合一部分作图要求的点的轨迹;
②再找出符合另一部分作图要求的点的轨迹;
③然后得出这两个轨迹的交点.
练习1 如图,已知∠AOB及点E、F,求作点P,
使点P到OA、OB的距离相等,且PE=PF.
A
E
O
B
F
P
牛刀小试
∴点P就是所求作的点.
作法:
2.联结EF,作线段EF
的垂直平分线
1.作∠AOB的平分线.
3.线段EF的垂直平分线
与∠AOB的平分线交于
点P.
练习2 如图,已知∠MON及线段a,点G在OM上,
作点P,使点P到OM、ON的距离相等,且PG=a.
a
O
M
N
G
P1
P2
∴点P1,P2就是所求作的点.
牛刀小试
作法:
2.以点G为圆心,
a为半径作圆
1.作∠MON的平分线.
3.∠MON的平分线与圆
交于点P1,P2.
问1:画一个三角形关键是确定其三个顶点,
本题中可先确定哪些顶点?
例题4 已知线段 a、h,求作等腰三角形,使其底边长
为a,底边上的高为h.
例题讲解
可先确定等腰三角形的底边的两个端点,
设为BC,BC=a.
问2:顶点A满足什么条件?
AB=AC.
说明点A在线段BC的垂直平分线上,
问3:底边上的高为h?
说明AD=h
∴△ABC就是所
求作的三角形.
例题讲解
例题5 要在某天然气管道MN上修建一个泵站,
分别向A、B两镇供气,泵站修在管道的什么地方,
可使所用的输气管线最短?
B
N
A
M
P
联结线段AB,
交直线MN于点P.
作法:
∴点P就是所求作的点.
P
两点之间线段最短.
理由:
PA+PB最小?
例题讲解
变式 要在某天然气管道MN上修建一个泵站,
分别向A、B两镇供气,泵站修在管道的什么地方,
可使所用的输气管线最短?
B
N
M
A
作法:
1.作点A关于MN的对称点A’.
A’
P
PA+PB最小?
PA'+PB最小?
√
√
P
2.联结A’B,与MN交于点P.
∴点P就是所求作的点.
利用轨迹相交进行作图的方法叫做交轨法.
步骤:
①先找出符合一部分作图要求的点的轨迹;
②再找出符合另一部分作图要求的点的轨迹;
③然后得出这两个轨迹的交点.
作图时,保留作图痕迹
归纳
再见
