22.1.2二次函数y=ax2的图象与性质课件 (共19张PPT) 2023-2024学年人教版数学九年级上册
文档属性
| 名称 | 22.1.2二次函数y=ax2的图象与性质课件 (共19张PPT) 2023-2024学年人教版数学九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 605.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-24 00:00:00 | ||
图片预览



文档简介
(共19张PPT)
第2课 二次函数y=ax2的图象与性质
第二十二章 二次函数
回顾旧知
1、二次函数的一般形式是:
y=ax2+bx+c(a≠0)
强调:
①、二次项系数a不等于0
②、自变量x的最高次数为2
③、一定是整式。
2、学习一次函数时,我们是通过画出函数的图象来研究它的性质,那么画图的步骤有哪些?
回顾旧知
列表、描点、连线
回顾旧知
3、你认为最简单的二次函数的形式是什么?
y=ax2(a≠0)
此时 b=0,c=0
研究二次函数 y=ax2(a≠0)也是从画图开始。
讲授新知
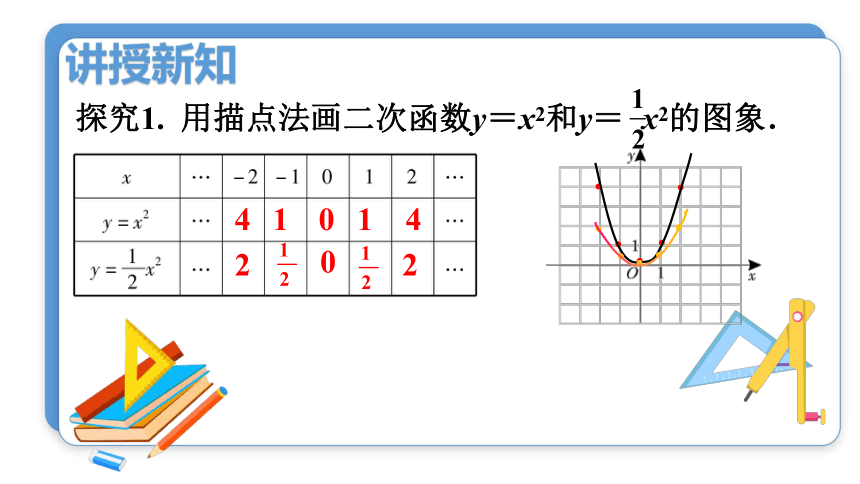
探究1. 用描点法画二次函数y=x2和y= x2的图象.
4
1
0
1
4
2
0
2
·
·
·
·
·
·
·
·
·
·
讲授新知
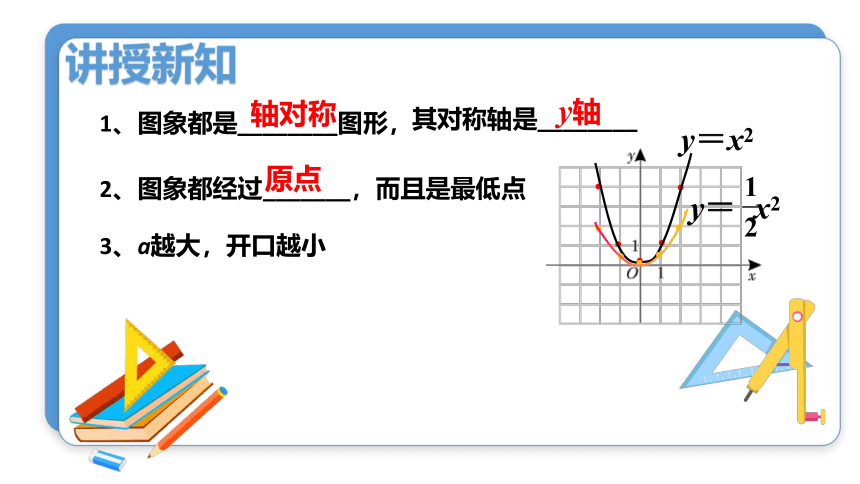
2、图象都经过_______,而且是最低点
原点
1、图象都是________图形,
轴对称
其对称轴是________
y轴
·
·
·
·
·
·
·
·
·
·
y=x2
y= x2
3、a越大,开口越小
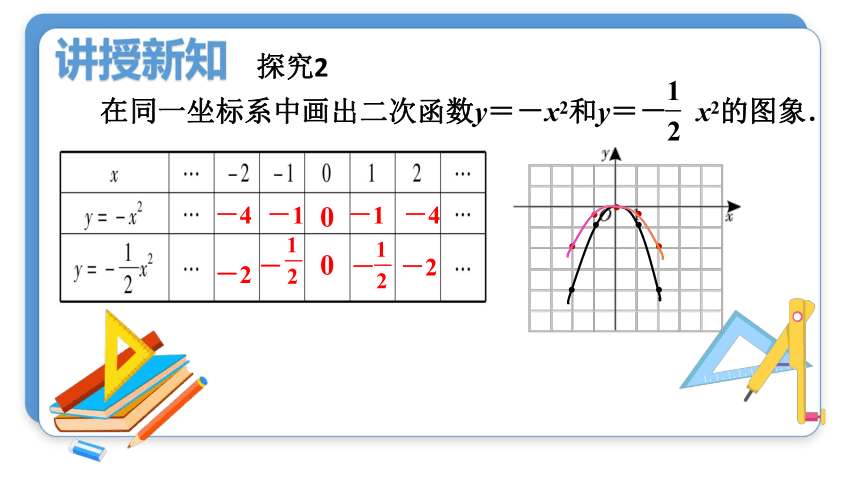
在同一坐标系中画出二次函数y=-x2和y=- x2的图象.
讲授新知
-4
-1
0
-1
-4
-2
-
0
-
-2
探究2
·
·
·
·
·
·
·
·
·
·
在同一坐标系中画出二次函数y=-x2和y=- x2的图象.
讲授新知
探究2
·
·
·
·
·
·
·
·
·
·
1、图象都是________图形,
轴对称
其对称轴是______
y轴
2、图象都经过_______,而且是最高点
原点
3、|a|越大,开口越小
总结:二次函数y=ax2的图象叫做_______.
抛物线
向上
向下
(0,0)
(0,0)
y轴
y轴
0
0
0
0
增大
减小
减小
增大
巩固新知
1、二次函数y=2x2的图象如图所示,则:
(1) 开口向___; (2)对称轴是____; (3)顶点坐标是______; (4)当x=___时,y的最小值=____;
(5)当x>0时,y随x的增大而______.
x
y
O
上
y轴
(0,0)
0
0
增大
2. 已知抛物线y=- x2,则:
(1)开口向___;
(2)对称轴是______; (3)顶点坐标是______; (4)当x=___时,y的最___值=___; (5)当x_____时,y随x的增大而增大.
巩固新知
下
y轴
(0,0)
0
大
0
<0
x
y
O
3.抛物线y=2x2,y=-2x2,y= x2共有的性质是 ( )
A.开口向下
B.对称轴是y轴
C.都有最低点
D.y随x的增大而减小
巩固新知
B
考虑a的正负
考虑顶点和开口方向
对称轴把抛物线一分为二,分开考虑。
巩固新知
4、已知二次函数y=(a-1)x2,当x>0时,y随x增大而增大,则实数a的取值范围是 ( )
A.a>0
B.a>1
C.a≠1
D.a<1
B
5、当x>0时,y随x增大而减小的函数是 ( )
A.y=x
B.y=2x-2
C.y=-x2
D.y=x2
巩固新知
C
通过画图象简图
6、已知点(x1,y1)与(x2,y2)在抛物线y=-2x2上,若x1<x2<0,则y1____y2.
巩固新知
所以当x<0时,y随x的增大而增大
a=-2<0,开口向下
<
拓展新知
如图,二次函数y=ax2(a≠0)与一次函数y=kx-2的图象相交于A,B两点,其中A(-1,-1),求 AOB的面积。
O
A
G
B
拓展新知
解:把A(-1,-1)代入y=kx-2,得
-k-2=-1
∴ k=-1
故一次函数的解析式为y=-x-2
把A(-1,-1)代入y=ax2,得
∴ a=-1
故二次函数的解析式为y=-x2
O
A
G
B
拓展新知
y=-x-2
y=-x2
解方程组 得
x1=-1
y1=-1
x2=2
y2=-4
∴ G的坐标为(0,-2)
O
A
G
B
当x=0时,y=-x-2=0-2=-2
∴ B的坐标为(2,-4)
拓展新知
O
A
G
B
∴ S AOB=S AOG+S BOG
=|-2|×|-1|÷2+|-2|×2÷2
=1+2=3
思考:还有其它的解法吗?
第2课 二次函数y=ax2的图象与性质
第二十二章 二次函数
回顾旧知
1、二次函数的一般形式是:
y=ax2+bx+c(a≠0)
强调:
①、二次项系数a不等于0
②、自变量x的最高次数为2
③、一定是整式。
2、学习一次函数时,我们是通过画出函数的图象来研究它的性质,那么画图的步骤有哪些?
回顾旧知
列表、描点、连线
回顾旧知
3、你认为最简单的二次函数的形式是什么?
y=ax2(a≠0)
此时 b=0,c=0
研究二次函数 y=ax2(a≠0)也是从画图开始。
讲授新知
探究1. 用描点法画二次函数y=x2和y= x2的图象.
4
1
0
1
4
2
0
2
·
·
·
·
·
·
·
·
·
·
讲授新知
2、图象都经过_______,而且是最低点
原点
1、图象都是________图形,
轴对称
其对称轴是________
y轴
·
·
·
·
·
·
·
·
·
·
y=x2
y= x2
3、a越大,开口越小
在同一坐标系中画出二次函数y=-x2和y=- x2的图象.
讲授新知
-4
-1
0
-1
-4
-2
-
0
-
-2
探究2
·
·
·
·
·
·
·
·
·
·
在同一坐标系中画出二次函数y=-x2和y=- x2的图象.
讲授新知
探究2
·
·
·
·
·
·
·
·
·
·
1、图象都是________图形,
轴对称
其对称轴是______
y轴
2、图象都经过_______,而且是最高点
原点
3、|a|越大,开口越小
总结:二次函数y=ax2的图象叫做_______.
抛物线
向上
向下
(0,0)
(0,0)
y轴
y轴
0
0
0
0
增大
减小
减小
增大
巩固新知
1、二次函数y=2x2的图象如图所示,则:
(1) 开口向___; (2)对称轴是____; (3)顶点坐标是______; (4)当x=___时,y的最小值=____;
(5)当x>0时,y随x的增大而______.
x
y
O
上
y轴
(0,0)
0
0
增大
2. 已知抛物线y=- x2,则:
(1)开口向___;
(2)对称轴是______; (3)顶点坐标是______; (4)当x=___时,y的最___值=___; (5)当x_____时,y随x的增大而增大.
巩固新知
下
y轴
(0,0)
0
大
0
<0
x
y
O
3.抛物线y=2x2,y=-2x2,y= x2共有的性质是 ( )
A.开口向下
B.对称轴是y轴
C.都有最低点
D.y随x的增大而减小
巩固新知
B
考虑a的正负
考虑顶点和开口方向
对称轴把抛物线一分为二,分开考虑。
巩固新知
4、已知二次函数y=(a-1)x2,当x>0时,y随x增大而增大,则实数a的取值范围是 ( )
A.a>0
B.a>1
C.a≠1
D.a<1
B
5、当x>0时,y随x增大而减小的函数是 ( )
A.y=x
B.y=2x-2
C.y=-x2
D.y=x2
巩固新知
C
通过画图象简图
6、已知点(x1,y1)与(x2,y2)在抛物线y=-2x2上,若x1<x2<0,则y1____y2.
巩固新知
所以当x<0时,y随x的增大而增大
a=-2<0,开口向下
<
拓展新知
如图,二次函数y=ax2(a≠0)与一次函数y=kx-2的图象相交于A,B两点,其中A(-1,-1),求 AOB的面积。
O
A
G
B
拓展新知
解:把A(-1,-1)代入y=kx-2,得
-k-2=-1
∴ k=-1
故一次函数的解析式为y=-x-2
把A(-1,-1)代入y=ax2,得
∴ a=-1
故二次函数的解析式为y=-x2
O
A
G
B
拓展新知
y=-x-2
y=-x2
解方程组 得
x1=-1
y1=-1
x2=2
y2=-4
∴ G的坐标为(0,-2)
O
A
G
B
当x=0时,y=-x-2=0-2=-2
∴ B的坐标为(2,-4)
拓展新知
O
A
G
B
∴ S AOB=S AOG+S BOG
=|-2|×|-1|÷2+|-2|×2÷2
=1+2=3
思考:还有其它的解法吗?
同课章节目录
