高二(上)期中数学试卷(含答案)
文档属性
| 名称 | 高二(上)期中数学试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 943.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-24 06:03:13 | ||
图片预览



文档简介
高二(上)期中数学试卷
一.选择题(共8小题,满分40分,每小题5分)
1.(5分)已知空间向量,则向量在坐标平面Oyz上的投影向量是( )
A.(0,2,3) B.(0,2,﹣3) C.(1,2,0) D.(1,2,﹣3)
2.(5分)已知过坐标原点的直线l经过点,直线n的倾斜角是直线l的2倍,则直线n的斜率是( )
A. B. C. D.
3.(5分)平面α的法向量=(1,2,﹣1),平面β的法向量=(λ2,2,8),若α⊥β,则λ的值是( )
A.2 B.﹣2 C.±2 D.不存在
4.(5分)过A(0,1),B(0,3)两点,且与直线y=x﹣1相切的圆的方程可以是( )
A.(x+1)2+(y﹣2)2=2 B.(x﹣2)2+(y﹣2)2=5
C.(x﹣1)2+(y﹣2)2=2 D.(x+2)2+(y﹣2)2=5
5.(5分)在长方体ABCD﹣A1B1C1D1中,M为棱CC1的中点.若=,=,=,则等于( )
A.++ B.﹣+ C.++ D.﹣+
6.(5分)已知直线l与圆C:x2+y2﹣6x+5=0交于A,B两点,且线段AB的中点坐标为D(2,),则|AB|=( )
A.2 B.3 C.4 D.5
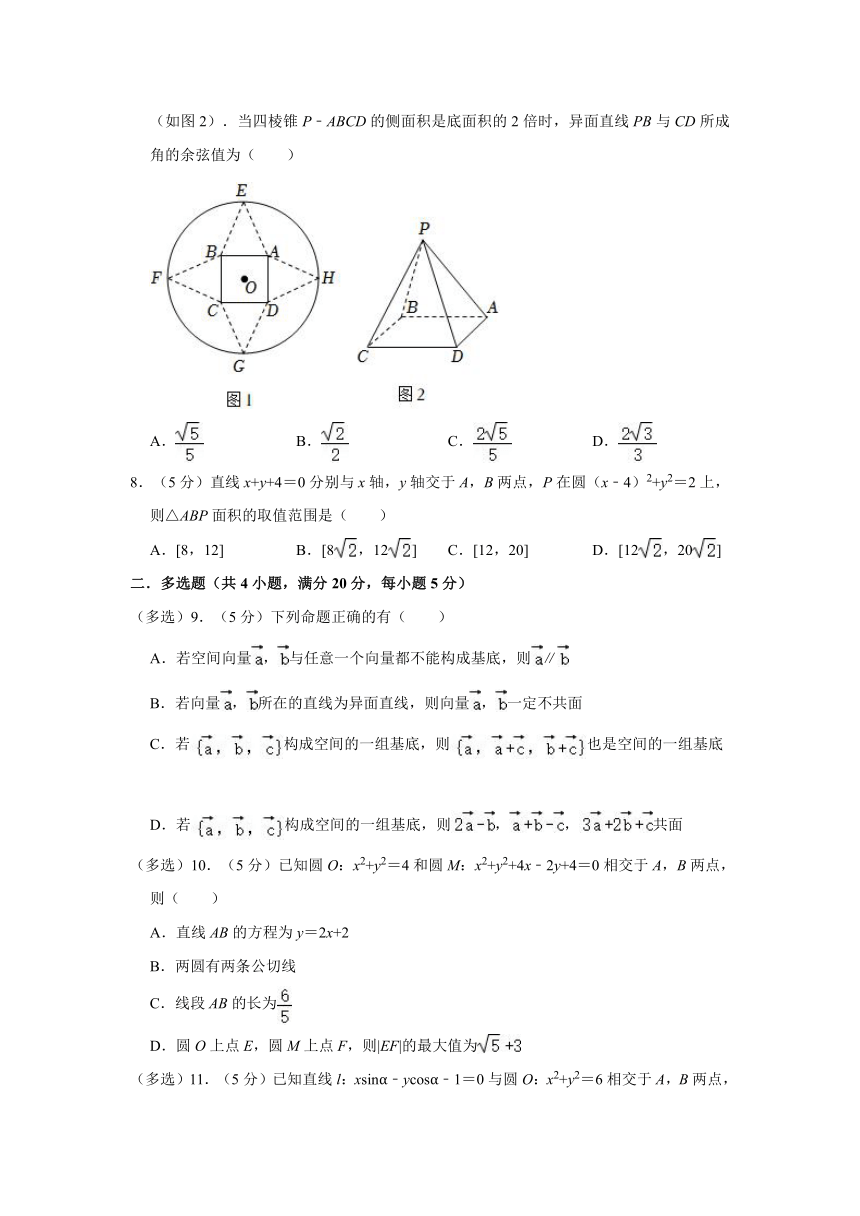
7.(5分)如图1,圆形纸片的圆心为O,半径为6cm,该纸片上的正方形ABCD的中心为O.点E,F,G,H为圆O上的点,△ABE,△BCF,△CDG,△ADH分别是以AB,BC,CD,DA为底边的等腰三角形.沿虚线剪开后,分别以AB,BC,CD,DA为折痕折起△ABE,△BCF,△CDG,△ADH,使得E,F,G,H重合得到一个四棱锥P﹣ABCD(如图2).当四棱锥P﹣ABCD的侧面积是底面积的2倍时,异面直线PB与CD所成角的余弦值为( )
A. B. C. D.
8.(5分)直线x+y+4=0分别与x轴,y轴交于A,B两点,P在圆(x﹣4)2+y2=2上,则△ABP面积的取值范围是( )
A.[8,12] B.[8,12] C.[12,20] D.[12,20]
二.多选题(共4小题,满分20分,每小题5分)
(多选)9.(5分)下列命题正确的有( )
A.若空间向量,与任意一个向量都不能构成基底,则∥
B.若向量,所在的直线为异面直线,则向量,一定不共面
C.若构成空间的一组基底,则也是空间的一组基底
D.若构成空间的一组基底,则,,共面
(多选)10.(5分)已知圆O:x2+y2=4和圆M:x2+y2+4x﹣2y+4=0相交于A,B两点,则( )
A.直线AB的方程为y=2x+2
B.两圆有两条公切线
C.线段AB的长为
D.圆O上点E,圆M上点F,则|EF|的最大值为
(多选)11.(5分)已知直线l:xsinα﹣ycosα﹣1=0与圆O:x2+y2=6相交于A,B两点,则( )
A.△AOB的面积为定值
B.cos∠AOB=﹣
C.圆O上总存在3个点到直线l的距离为2
D.线段AB中点的轨迹方程是x2+y2=1
(多选)12.(5分)如图,在正四棱柱ABCD﹣A1B1C1D1中,底面边长,侧棱长,P为底面ABCD内的动点,且A1P与BB1所成角为30°,则下列命题正确的是( )
A.动点P的轨迹长度为
B.当B1P∥平面A1C1D时,B1P与平面A1C1D的距离为
C.直线C1P与底面ABCD所成角的最大值为
D.二面角P﹣A1C1﹣D的范围是
三.填空题(共4小题,满分20分,每小题5分)
13.(5分)已知直线l1:ax+2y+3a﹣2=0与l2:x+(a+1)y+4=0平行,则实数a的值为 .
14.(5分)给出以下命题:
①空间任意两个共起点的向量是共面的;
②两个相等向量就是相等长度的两条有向线段表示的向量;
③空间向量的加法满足结合律:(+)+=+(+);
④首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.
上述命题中,真命题的序号是 .
15.(5分)已知直线l1与直线l2:3x+4y﹣6=0平行,且与圆x2+y2+2y=0相切,则直线l1的方程是 .
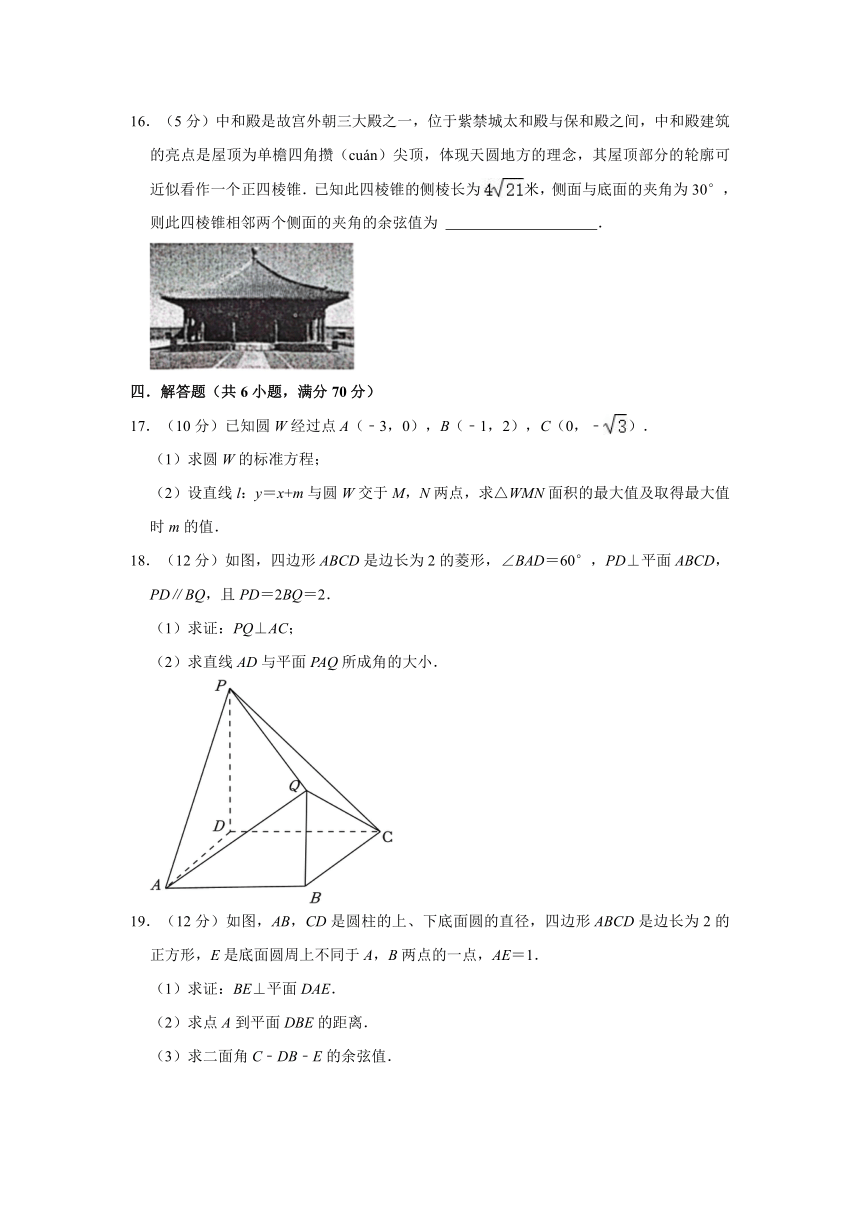
16.(5分)中和殿是故宫外朝三大殿之一,位于紫禁城太和殿与保和殿之间,中和殿建筑的亮点是屋顶为单檐四角攒(cuán)尖顶,体现天圆地方的理念,其屋顶部分的轮廓可近似看作一个正四棱锥.已知此四棱锥的侧棱长为米,侧面与底面的夹角为30°,则此四棱锥相邻两个侧面的夹角的余弦值为 .
四.解答题(共6小题,满分70分)
17.(10分)已知圆W经过点A(﹣3,0),B(﹣1,2),C(0,﹣).
(1)求圆W的标准方程;
(2)设直线l:y=x+m与圆W交于M,N两点,求△WMN面积的最大值及取得最大值时m的值.
18.(12分)如图,四边形ABCD是边长为2的菱形,∠BAD=60°,PD⊥平面ABCD,PD∥BQ,且PD=2BQ=2.
(1)求证:PQ⊥AC;
(2)求直线AD与平面PAQ所成角的大小.
19.(12分)如图,AB,CD是圆柱的上、下底面圆的直径,四边形ABCD是边长为2的正方形,E是底面圆周上不同于A,B两点的一点,AE=1.
(1)求证:BE⊥平面DAE.
(2)求点A到平面DBE的距离.
(3)求二面角C﹣DB﹣E的余弦值.
20.(12分)已知圆C:x2+y2﹣2x﹣4y+m=0.
(1)若圆C与圆x2+y2﹣8x﹣12y+36=0外切,求m的值;
(2)当m=1时,由直线l:x﹣y+4=0上任意一点P作圆C的两条切线PA,PB(A,B为切点),试探究四边形PACB的外接圆是否过定点?若过,求出该点的坐标;若不过,请说明理由.
21.(12分)如图,四棱锥E﹣ABCD,,CD=CB=1,AC=2,平面EAC⊥平面ABCD,平面ABE∩平面CDE=l.
(1)若点M为线段AE中点,求证:BM∥l;
(2)若∠ACE=60°,CE=1,求直线BC与平面ADE所成角的正弦值.
22.(12分)已知圆C过点A(6,0),B(1,5),且圆心在直线l:2x﹣7y+8=0上.
(1)求圆C的标准方程;
(2)过点D(0,5)且斜率为k的直线l与圆C有两个不同的交点M,N,若,其中O为坐标原点,求直线l的方程.
高二(上)期中数学试卷
参考答案与解析
一.选择题(共8小题,满分40分,每小题5分)
1.B.
2.A.
3.C.
4.C.
5.A.
6.A.
7.A.
8.C.
二.多选题(共4小题,满分20分,每小题5分)
9.AC.
10.BD.
11.ABD.
12.AC.
三.填空题(共4小题,满分20分,每小题5分)
13.1.
14.①③④.
15.3x+4y﹣1=0或3x+4y+9=0.
16..
四.解答题(共6小题,满分70分)
17.解:(1)设圆W的标准方程为(x﹣a)2+(y﹣b)2=r2(r>0),
则有,解得,
所以圆W的标准方程为(x+1)2+y2=4;
(2)圆W的圆心W(﹣1,0),半径r=2,圆心W到直线l的距离d=,
因为直线1:y=x+m与圆W交于M,N两点,
所以0<<2,解得﹣2+1<m<2+1且m≠1,
|MN|=2=2,
则S△WMN=d|MN|=d =,
所以令t=d2,t∈(0,4),
则S△WMN==≤2,
所以当t=2时,即d=,此时=,即m=3或﹣1时,
△WMN面积取得最大值2,
所以当m=3或﹣1时,△WMN面积取得最大值2.
18.(1)证明:连接BD,因为四边形ABCD是菱形,
所以AC⊥BD,
又因为PD⊥平面ABCD,AC 平面ABCD,
所以AC⊥PD,
又BD∩PD=D,所以AC⊥平面PDBQ,
因为PQ 平面PDBQ,所以PQ⊥AC.
解:(2)设AC∩BD=O,取PQ的中点M,则OM∥PD,
由(1)知,AC⊥BD,AC⊥OM.
以O为坐标原点,以OA,OB,OM所在直线为x,y,z轴建立空间直角坐标系,
则.
所以,,
设平面PAQ的一个法向量,则,所以,
所以,取.
设直线AD与平面PAQ夹角为α,
所以,,
所以,
即直线AD与平面PAQ夹角的大小为.
19.解:(1)证明:AB,CD是圆柱的上、下底面圆的直径,四边形ABCD是边长为2的正方形,
E是底面圆周上不同于A,B两点的一点,AE=1.
∴BE⊥AE,BE⊥AD,
∵AE∩AD=A,∴BE⊥平面DAE.
(2)解法一:∵边形ABCD是边长为2的正方形,AE=1.
∴BE==,DE==,
设点A到平面DBE的距离为h,
∵VD﹣ABE=VA﹣BDE,∴=,
∴h===.
∴点A到平面DBE的距离.
解法二:∵BE⊥平面DAE,∴AE⊥BE,
∴点A到DE的距离即点A到平面BDE的距离,
在Rt△ADE中,点A到BD的距离为:
d===,
∴点A到平面DBE的距离为.
(3)解:以E为原点,EB为x轴,EA为y轴,过点E作平面ABE的垂线为z轴,建立空间直角坐标系,
B(,0,0),D(0,1,2),C(,0,2),E(0,0,0),
=(﹣,1,2),=(0,0,2),=(,0,0),=(0,1,2),
设平面BCD的法向量为=(x,y,z),
则,取x=1,得=(1,,0),
设平面BDE的法向量=(a,b,c),
则,取b=2,得=(0,2,﹣1),
设二面角C﹣DB﹣E的平面角为θ,
则cosθ===.
∴二面角C﹣DB﹣E的余弦值为.
20.解:(1)∵圆C方程可化为:(x﹣1)2+(y﹣2)2=5﹣m,(m<5),
∴圆心C(1,2),半径r=,
又圆D:x2+y2﹣8x﹣12y+36=0可化为:(x﹣4)2+(y﹣6)2=16,
∴圆心D(4,6),半径R=4,又两圆外切,
∴|CD|=r+R,
∴,(m<5),
解得m=4;
(2)当m=1时,圆C方程可化为:(x﹣1)2+(y﹣2)2=4,
由圆的切线的性质易得:四边形PACB的外接圆为以PC为直径的圆,
∴四边形PACB的外接圆是过定点C(1,2).
21.解:(1)证明:如图,设AD,AC中点分别为F,G,连接MF,FG,GB,又点M为线段AE中点,
∴MF∥ED,FG∥DC,又GC=AC=1=BC,又由,CD=CB=1,AC=2,得cos∠ACD=cos,∴∠ACD=,
∴△BCG为等边三角形,∴,又∠AGF=∠ACD=,∴∠AGF=CGB=,∴F,G,B三点共线,
∴MF∥ED,FB∥DC,又MF∩FB=B,∴平面MBG∥平面EDC,又MB 平面MBG,
∴MB∥平面EDC,又MB 平面ABE,且平面ABE∩平面CDE=l,
∴BM∥l;
(2)如图,由题意知AC⊥BD,又平面EAC⊥平面ABCD,过E作EO垂直AC于点O,则EO⊥平面ABCD,
又∠ACE=60°,CE=1,∴OE=CE sin60°=,OC=CE cos60°==,∴O为GC的中点,易知四边形GBCD为一个角为60°的菱形,∴O在BD上,
且AO=AC﹣OC=2﹣=,OD=OB=,
分别以直线DB,AC,OE为x,y,z轴建立空间右手直角坐标系,则B(,0,0),C(0,,0),A(0,,0),D(,0,0),E(0,0,),
∴=(,,0),=(0,,),=(,,0),设平面ADE的一个法向量为:,
则,令,则y=2,,∴,设直线BC与平面ADE所成角为θ,
∴sinθ===,
∴直线BC与平面ADE所成角的正弦值为.
22.解:(1)∵A(6,0),B(1,5),
∴AB的中点为(,),AB的斜率为=﹣1,
∴AB的垂直平分线方程为:y﹣=x﹣,即x﹣y﹣1=0,
联立,解得,
∴圆心C为(3,2),半径r=CA==,
∴圆C的标准方程为(x﹣3)2+(y﹣2)2=13;
(2)根据题意可设直线l方程为y=kx+5,
联立圆C:(x﹣3)2+(y﹣2)2=13可得:
(k2+1)x2+6(k﹣1)x+5=0,设M(x1,y1),N(x2,y2),
则,,
∴y1y2=(kx1+5)(kx2+5)=k2x1x2+5k(x1+x2)+25,
∴=x1x2+y1y2=(k2+1)x1x2+5k(x1+x2)+25=30,
∴,
解得k=0或k=1,经检验k=1时,直线与圆相切,不满足题意,
∴k=0,
∴直线l的方程为y=5
一.选择题(共8小题,满分40分,每小题5分)
1.(5分)已知空间向量,则向量在坐标平面Oyz上的投影向量是( )
A.(0,2,3) B.(0,2,﹣3) C.(1,2,0) D.(1,2,﹣3)
2.(5分)已知过坐标原点的直线l经过点,直线n的倾斜角是直线l的2倍,则直线n的斜率是( )
A. B. C. D.
3.(5分)平面α的法向量=(1,2,﹣1),平面β的法向量=(λ2,2,8),若α⊥β,则λ的值是( )
A.2 B.﹣2 C.±2 D.不存在
4.(5分)过A(0,1),B(0,3)两点,且与直线y=x﹣1相切的圆的方程可以是( )
A.(x+1)2+(y﹣2)2=2 B.(x﹣2)2+(y﹣2)2=5
C.(x﹣1)2+(y﹣2)2=2 D.(x+2)2+(y﹣2)2=5
5.(5分)在长方体ABCD﹣A1B1C1D1中,M为棱CC1的中点.若=,=,=,则等于( )
A.++ B.﹣+ C.++ D.﹣+
6.(5分)已知直线l与圆C:x2+y2﹣6x+5=0交于A,B两点,且线段AB的中点坐标为D(2,),则|AB|=( )
A.2 B.3 C.4 D.5
7.(5分)如图1,圆形纸片的圆心为O,半径为6cm,该纸片上的正方形ABCD的中心为O.点E,F,G,H为圆O上的点,△ABE,△BCF,△CDG,△ADH分别是以AB,BC,CD,DA为底边的等腰三角形.沿虚线剪开后,分别以AB,BC,CD,DA为折痕折起△ABE,△BCF,△CDG,△ADH,使得E,F,G,H重合得到一个四棱锥P﹣ABCD(如图2).当四棱锥P﹣ABCD的侧面积是底面积的2倍时,异面直线PB与CD所成角的余弦值为( )
A. B. C. D.
8.(5分)直线x+y+4=0分别与x轴,y轴交于A,B两点,P在圆(x﹣4)2+y2=2上,则△ABP面积的取值范围是( )
A.[8,12] B.[8,12] C.[12,20] D.[12,20]
二.多选题(共4小题,满分20分,每小题5分)
(多选)9.(5分)下列命题正确的有( )
A.若空间向量,与任意一个向量都不能构成基底,则∥
B.若向量,所在的直线为异面直线,则向量,一定不共面
C.若构成空间的一组基底,则也是空间的一组基底
D.若构成空间的一组基底,则,,共面
(多选)10.(5分)已知圆O:x2+y2=4和圆M:x2+y2+4x﹣2y+4=0相交于A,B两点,则( )
A.直线AB的方程为y=2x+2
B.两圆有两条公切线
C.线段AB的长为
D.圆O上点E,圆M上点F,则|EF|的最大值为
(多选)11.(5分)已知直线l:xsinα﹣ycosα﹣1=0与圆O:x2+y2=6相交于A,B两点,则( )
A.△AOB的面积为定值
B.cos∠AOB=﹣
C.圆O上总存在3个点到直线l的距离为2
D.线段AB中点的轨迹方程是x2+y2=1
(多选)12.(5分)如图,在正四棱柱ABCD﹣A1B1C1D1中,底面边长,侧棱长,P为底面ABCD内的动点,且A1P与BB1所成角为30°,则下列命题正确的是( )
A.动点P的轨迹长度为
B.当B1P∥平面A1C1D时,B1P与平面A1C1D的距离为
C.直线C1P与底面ABCD所成角的最大值为
D.二面角P﹣A1C1﹣D的范围是
三.填空题(共4小题,满分20分,每小题5分)
13.(5分)已知直线l1:ax+2y+3a﹣2=0与l2:x+(a+1)y+4=0平行,则实数a的值为 .
14.(5分)给出以下命题:
①空间任意两个共起点的向量是共面的;
②两个相等向量就是相等长度的两条有向线段表示的向量;
③空间向量的加法满足结合律:(+)+=+(+);
④首尾相接的若干向量之和,等于由起始向量的起点指向末尾向量的终点的向量.
上述命题中,真命题的序号是 .
15.(5分)已知直线l1与直线l2:3x+4y﹣6=0平行,且与圆x2+y2+2y=0相切,则直线l1的方程是 .
16.(5分)中和殿是故宫外朝三大殿之一,位于紫禁城太和殿与保和殿之间,中和殿建筑的亮点是屋顶为单檐四角攒(cuán)尖顶,体现天圆地方的理念,其屋顶部分的轮廓可近似看作一个正四棱锥.已知此四棱锥的侧棱长为米,侧面与底面的夹角为30°,则此四棱锥相邻两个侧面的夹角的余弦值为 .
四.解答题(共6小题,满分70分)
17.(10分)已知圆W经过点A(﹣3,0),B(﹣1,2),C(0,﹣).
(1)求圆W的标准方程;
(2)设直线l:y=x+m与圆W交于M,N两点,求△WMN面积的最大值及取得最大值时m的值.
18.(12分)如图,四边形ABCD是边长为2的菱形,∠BAD=60°,PD⊥平面ABCD,PD∥BQ,且PD=2BQ=2.
(1)求证:PQ⊥AC;
(2)求直线AD与平面PAQ所成角的大小.
19.(12分)如图,AB,CD是圆柱的上、下底面圆的直径,四边形ABCD是边长为2的正方形,E是底面圆周上不同于A,B两点的一点,AE=1.
(1)求证:BE⊥平面DAE.
(2)求点A到平面DBE的距离.
(3)求二面角C﹣DB﹣E的余弦值.
20.(12分)已知圆C:x2+y2﹣2x﹣4y+m=0.
(1)若圆C与圆x2+y2﹣8x﹣12y+36=0外切,求m的值;
(2)当m=1时,由直线l:x﹣y+4=0上任意一点P作圆C的两条切线PA,PB(A,B为切点),试探究四边形PACB的外接圆是否过定点?若过,求出该点的坐标;若不过,请说明理由.
21.(12分)如图,四棱锥E﹣ABCD,,CD=CB=1,AC=2,平面EAC⊥平面ABCD,平面ABE∩平面CDE=l.
(1)若点M为线段AE中点,求证:BM∥l;
(2)若∠ACE=60°,CE=1,求直线BC与平面ADE所成角的正弦值.
22.(12分)已知圆C过点A(6,0),B(1,5),且圆心在直线l:2x﹣7y+8=0上.
(1)求圆C的标准方程;
(2)过点D(0,5)且斜率为k的直线l与圆C有两个不同的交点M,N,若,其中O为坐标原点,求直线l的方程.
高二(上)期中数学试卷
参考答案与解析
一.选择题(共8小题,满分40分,每小题5分)
1.B.
2.A.
3.C.
4.C.
5.A.
6.A.
7.A.
8.C.
二.多选题(共4小题,满分20分,每小题5分)
9.AC.
10.BD.
11.ABD.
12.AC.
三.填空题(共4小题,满分20分,每小题5分)
13.1.
14.①③④.
15.3x+4y﹣1=0或3x+4y+9=0.
16..
四.解答题(共6小题,满分70分)
17.解:(1)设圆W的标准方程为(x﹣a)2+(y﹣b)2=r2(r>0),
则有,解得,
所以圆W的标准方程为(x+1)2+y2=4;
(2)圆W的圆心W(﹣1,0),半径r=2,圆心W到直线l的距离d=,
因为直线1:y=x+m与圆W交于M,N两点,
所以0<<2,解得﹣2+1<m<2+1且m≠1,
|MN|=2=2,
则S△WMN=d|MN|=d =,
所以令t=d2,t∈(0,4),
则S△WMN==≤2,
所以当t=2时,即d=,此时=,即m=3或﹣1时,
△WMN面积取得最大值2,
所以当m=3或﹣1时,△WMN面积取得最大值2.
18.(1)证明:连接BD,因为四边形ABCD是菱形,
所以AC⊥BD,
又因为PD⊥平面ABCD,AC 平面ABCD,
所以AC⊥PD,
又BD∩PD=D,所以AC⊥平面PDBQ,
因为PQ 平面PDBQ,所以PQ⊥AC.
解:(2)设AC∩BD=O,取PQ的中点M,则OM∥PD,
由(1)知,AC⊥BD,AC⊥OM.
以O为坐标原点,以OA,OB,OM所在直线为x,y,z轴建立空间直角坐标系,
则.
所以,,
设平面PAQ的一个法向量,则,所以,
所以,取.
设直线AD与平面PAQ夹角为α,
所以,,
所以,
即直线AD与平面PAQ夹角的大小为.
19.解:(1)证明:AB,CD是圆柱的上、下底面圆的直径,四边形ABCD是边长为2的正方形,
E是底面圆周上不同于A,B两点的一点,AE=1.
∴BE⊥AE,BE⊥AD,
∵AE∩AD=A,∴BE⊥平面DAE.
(2)解法一:∵边形ABCD是边长为2的正方形,AE=1.
∴BE==,DE==,
设点A到平面DBE的距离为h,
∵VD﹣ABE=VA﹣BDE,∴=,
∴h===.
∴点A到平面DBE的距离.
解法二:∵BE⊥平面DAE,∴AE⊥BE,
∴点A到DE的距离即点A到平面BDE的距离,
在Rt△ADE中,点A到BD的距离为:
d===,
∴点A到平面DBE的距离为.
(3)解:以E为原点,EB为x轴,EA为y轴,过点E作平面ABE的垂线为z轴,建立空间直角坐标系,
B(,0,0),D(0,1,2),C(,0,2),E(0,0,0),
=(﹣,1,2),=(0,0,2),=(,0,0),=(0,1,2),
设平面BCD的法向量为=(x,y,z),
则,取x=1,得=(1,,0),
设平面BDE的法向量=(a,b,c),
则,取b=2,得=(0,2,﹣1),
设二面角C﹣DB﹣E的平面角为θ,
则cosθ===.
∴二面角C﹣DB﹣E的余弦值为.
20.解:(1)∵圆C方程可化为:(x﹣1)2+(y﹣2)2=5﹣m,(m<5),
∴圆心C(1,2),半径r=,
又圆D:x2+y2﹣8x﹣12y+36=0可化为:(x﹣4)2+(y﹣6)2=16,
∴圆心D(4,6),半径R=4,又两圆外切,
∴|CD|=r+R,
∴,(m<5),
解得m=4;
(2)当m=1时,圆C方程可化为:(x﹣1)2+(y﹣2)2=4,
由圆的切线的性质易得:四边形PACB的外接圆为以PC为直径的圆,
∴四边形PACB的外接圆是过定点C(1,2).
21.解:(1)证明:如图,设AD,AC中点分别为F,G,连接MF,FG,GB,又点M为线段AE中点,
∴MF∥ED,FG∥DC,又GC=AC=1=BC,又由,CD=CB=1,AC=2,得cos∠ACD=cos,∴∠ACD=,
∴△BCG为等边三角形,∴,又∠AGF=∠ACD=,∴∠AGF=CGB=,∴F,G,B三点共线,
∴MF∥ED,FB∥DC,又MF∩FB=B,∴平面MBG∥平面EDC,又MB 平面MBG,
∴MB∥平面EDC,又MB 平面ABE,且平面ABE∩平面CDE=l,
∴BM∥l;
(2)如图,由题意知AC⊥BD,又平面EAC⊥平面ABCD,过E作EO垂直AC于点O,则EO⊥平面ABCD,
又∠ACE=60°,CE=1,∴OE=CE sin60°=,OC=CE cos60°==,∴O为GC的中点,易知四边形GBCD为一个角为60°的菱形,∴O在BD上,
且AO=AC﹣OC=2﹣=,OD=OB=,
分别以直线DB,AC,OE为x,y,z轴建立空间右手直角坐标系,则B(,0,0),C(0,,0),A(0,,0),D(,0,0),E(0,0,),
∴=(,,0),=(0,,),=(,,0),设平面ADE的一个法向量为:,
则,令,则y=2,,∴,设直线BC与平面ADE所成角为θ,
∴sinθ===,
∴直线BC与平面ADE所成角的正弦值为.
22.解:(1)∵A(6,0),B(1,5),
∴AB的中点为(,),AB的斜率为=﹣1,
∴AB的垂直平分线方程为:y﹣=x﹣,即x﹣y﹣1=0,
联立,解得,
∴圆心C为(3,2),半径r=CA==,
∴圆C的标准方程为(x﹣3)2+(y﹣2)2=13;
(2)根据题意可设直线l方程为y=kx+5,
联立圆C:(x﹣3)2+(y﹣2)2=13可得:
(k2+1)x2+6(k﹣1)x+5=0,设M(x1,y1),N(x2,y2),
则,,
∴y1y2=(kx1+5)(kx2+5)=k2x1x2+5k(x1+x2)+25,
∴=x1x2+y1y2=(k2+1)x1x2+5k(x1+x2)+25=30,
∴,
解得k=0或k=1,经检验k=1时,直线与圆相切,不满足题意,
∴k=0,
∴直线l的方程为y=5
同课章节目录
