五四制鲁教版八年级上册期末测试数学卷(含解析)
文档属性
| 名称 | 五四制鲁教版八年级上册期末测试数学卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 7.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-23 22:33:04 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
五四制鲁教版数学八年级上册期末测试卷
一、选择题(本大题共36分,每小题3分)
1 . 2022年,中国航天迈着大步向浩瀚宇宙不断探索,神舟十四号载人飞船成功发射,世界首幅1:250 万月球全月地质图完成,我国首颗陆地生态系统碳监测卫星“句芒号”成功发射 下列航天图标,是中心对称图形的是( )
2.下列由左到右变形,属于因式分解且分解正确的是( )
3.若把x,y的值同时扩大为原来的2倍,则下列分式的值保持不变的是( )
4.若正多边形的内角和是1260°,则该正多边形的一个外角为( )
A.30° B.40° C.45° D.60°
5.某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是( )
A.甲种方案所用铁丝最长 B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长 D.三种方案所用铁丝一样长
6.四边形 ABCD中,对角线AC,BD相交于点O,给出下列四个条件:
①AD∥BC;②AD=BC;③OA=OC;④OB=OD.
从中任选两个条件能使四边形 ABCD为平行四边形的选法有( )
A.3种 B.4种 C.5种 D.6种
7.小明家1月至6月的用水量统计图如图所示,关于这组数据,下列说法错误的是( )
A.中位数是 5 吨 B.众数是6吨 C.平均数是 5吨 D.方差是
8.假期正是读书的好时候,小颖同学到重庆图书馆借了一本书,共280页,要在两周借期内读完,当她读了一半时,发现以后平均每天要多读21页才能在借期内读完,她读前一半时,平均每天读多少页 如果设读前一半时,平均每天读x页,则下面所列方程中,正确的是( )
9.如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE 是△ABC 的中位线,延长 DE 交△ABC
的外角∠ACM的平分线于点 F,则线段 DF的长为( )
A.7 B.8 C.9 D.10
第9题图 第10题图
10.如图,在平行四边形 ABCD中,∠B=60°,将△ABC沿AC 折叠,点 B的对应点落在点 E处,且点 B,A,E在一条直线上,CE交AD于点 F,则图中等边三角形共有( )
A.4个 B.3个 C.2个 D.1个
11.若 m+n-p=0,则 的值是( )
A.-3 B.-1 C.1 D.3
12.如图,在等腰直角三角形ABC中,∠C=90°,点O是AB的中点,且 将一块直角三角板的直角顶点放在点 O 处,将直角三角板绕点O 旋转,且在旋转过程中始终保持该直角三角板的两直角边分别与 AC,BC 相交,交点分别为点 D,E,则CD+CE=( )
A. C.2 D.
二、填空题(本大题共12分,每小题2分)
13.代数式 有意义时,x应满足的条件为_____________.
14 如图,在 ABCD中,点 E在 BC 边上,且AE⊥BC于点 E,DE 平分∠CDA.若 BE:EC=1:2,则∠BCD 的度数为____________.
15.某次跳绳比赛中,统计甲、乙两班学生每分钟跳绳的成绩(单位:次)情况如下表:
班级 参加人数 平均次数 中位数 方差
甲班 45 135 149 180
乙班 45 135 151 130
有下面三个命题:
①甲班平均成绩低于乙班平均成绩;
②甲班成绩的波动比乙班成绩的波动大;
③甲班成绩优秀人数少于乙班成绩优秀人数.(每分钟跳绳的成绩大于等于 150次为优秀).
其中正确的命题是_______________.(只填序号)
16.若关于x的分式方程 的解为非负数,则m的取值范围是__________.
17.如图,边长为4的等边三角形 ABC中,E是对称轴AD上的一个动点,连接 CE,将线段 CE 绕点C顺时针旋转60°得到CF,连接 DF,则在点 E运动过程中,DF的最小值是____________.
第17题图 第18题图
18.某快递公司快递员甲匀速骑车去距公司6000米的某小区取物件,出发几分钟后,该公司快递员乙发现甲的手机落在公司,于是立马匀速骑车去追赶甲,乙出发几分钟后,甲也发现自己的手机落在了公司,立即调头以原速的2倍原路返回,1分钟后遇到了乙,乙把手机给甲后,乙以原速的一半原路返回公司,甲以返回时的速度继续去小区取物件,刚好在事先预计的时间到达该小区.甲、乙两人相距的路程y(米)与甲出发的时间x(分)之间的关系如图所示(给手机及中途其他耽误时间忽略不计),则甲到小区时,乙距公司的路程是___________米.
三、解答题(本大题共72分.解答应写出文字说明、演算步骤或证明过程)
19.(6分)(1)计算:(x+5)·(x-1)+(x-2) .
(2)因式分解:a (b-1)+b -b .
(3)解方程:
20.(6分)(1)计算:
(2)计算:
(3)先化简 然后从-1,1,2三个数中任选一个合适的a代入求值.
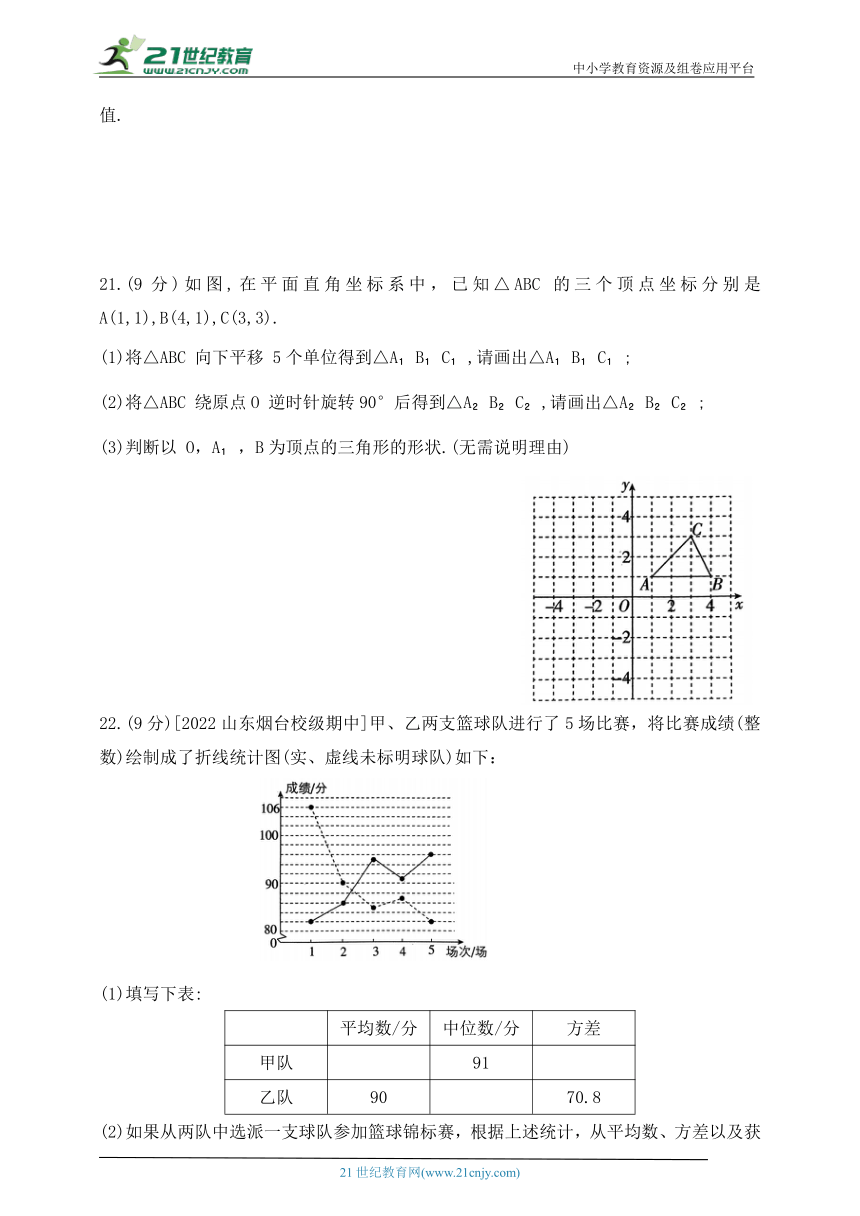
21.(9分)如图,在平面直角坐标系中,已知△ABC 的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC 向下平移 5个单位得到△A B C ,请画出△A B C ;
(2)将△ABC 绕原点O 逆时针旋转90°后得到△A B C ,请画出△A B C ;
(3)判断以 O,A ,B为顶点的三角形的形状.(无需说明理由)
22.(9分)[2022山东烟台校级期中]甲、乙两支篮球队进行了5场比赛,将比赛成绩(整数)绘制成了折线统计图(实、虚线未标明球队)如下:
(1)填写下表:
平均数/分 中位数/分 方差
甲队 91
乙队 90 70.8
(2)如果从两队中选派一支球队参加篮球锦标赛,根据上述统计,从平均数、方差以及获胜场数这三个方面分别进行简要分析,你认为选派哪支球队参赛更有可能取得好成绩
23.(10分)如图,在平面直角坐标系xOy中,点A的坐标为(-2,0),等边三角形 AOC 经过平移或轴对称或旋转都可以得到△OBD.
(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是_______个单位长度;△AOC与△BOD关于某直线对称,则对称轴是________;△AOC 绕原点 O 顺时针旋转得到△DOB,则最小旋转角是__________.
(2)如图,连接AD,交 OC于点E,求∠AEO 的度数.
24.(10分)近年来,电商平台直播带货成了一个火热的新兴职业. 春节期间,某直播销售员销售一种童装.这种童装的进价为每套 150元,若按原标价销售,则每周销售额为10000 元;若按原标价的八五折销售,则每周多卖出20套,且销售额还增加1900元.
(1)求每套童装的原标价为多少元;
(2)若按原标价的九折销售,该直播销售员想要每周获利不低于 2700元,求该直播销售员每周至少需卖出这种童装多少套.
25.(10分)如图,在 ABCD中,对角线 AC,BD相交于点O,AB⊥AC,AB=3cm,BC=5cm .点P从 A 点出发沿 AD 方向匀速运动,速度为1 cm/s,连接 PO 并延长交 BC 于点 Q.设运动时间为 ts(0(1)当t为何值时,四边形 ABQP 是平行四边形
(2)设四边形 OQCD 的面积为 y cm ,当t=4时,求y的值.
26.(12分)已知点 O 是等边△ABC 内的任意一点,连接 OA,OB,OC.
(1)如图所示,已知∠AOB=150°,∠BOC=120°,将△BOC绕点C按顺时针方向旋转60°得△ADC.
①求∠DAO的度数;
②猜想线段 OA,OB,OC之间的数量关系,并证明.
(2)设∠AOB=α,∠BOC=β.当α,β满足什么关系时,OA+OB+OC有最小值 并说明理由.
参考答案
1. B【解析】只有选项B能找到这样的一个点,使图形绕该点旋转180度后和原图形完全重合,所以是中心对称图形,故选B.
2. D 【解析】
A原变形是整式的乘法,不是因式分解,不符合题意;
B原变形错误,正确的是2x +4=2(x +2),不符合题意
C原变形错误,正确的是 不符合题意
D原变形符合因式分解的定义,且分解正确,符合题意
3. A【解析】 故选项 A的值保持不变. 故选项B的值不能保持不变.故选项 C的值不能保持不变. 故选项D的值不能保持不变.故选 A.
4. B【解析】设该正多边形的边数为 n.根据题意,得(n-2)·180°=1260°,解得 n=9,∴该正多边形的边数是9.∵多边形的外角和为360°,360°÷9=40°,∴该正多边形的一个外角为40°.故选B.
5. D【解析】题图中三个图形通过平移线段都可以得到边长分别为 a,b的长方形,所以其周长相等,所以三种方案用的铁丝的长度一样.
6. B【解析】从四个中任选两个,共有6种情况,具体如下表:
条件 四边形 ABCD是否为平行四边形
①② 是
①③ 是
①④ 是
②③ 否
②④ 否
③④ 是
7. A【解析】A 选项,这组数据按照从小到大的顺序排列为3,4,5,6,6,6,则这组数据的中位数是(5+6)÷2=5.5(吨),原来的说法错误,符合题意;B选项,众数是6吨,是正确的,不符合题意;C 选项,平均数为(4+6+3+5+6+6)÷6=(5)吨,是正确的,不符合题意;D选项,方差是 是正确的,不符合题意.故选A.
8. C【解析】读前一半用的时间为 天,读后一半用的时间为 天.由题意得, 故选C.
9. B【解析】∵∠ABC=90°,DE 是△ABC的中位线,AB=8,BC=6,∴DE 平行且等于 BC,AC=10,∴DE=3,CE = 5,∠FCM =∠CFE. ∵CF 平分∠ACM,∴∠ECF=∠FCM,∴∠ECF=∠CFE,∴EF=CE=5,∴DF=DE+EF=3+5=8.故选B.
10. B【解析】∵∠B=60°,将△ABC沿AC折叠,点B落在点E处,且点B,A,E在一条直线上,∴△BCE为等边三角形.∵AD∥BC,AB∥CD,易得△AEF和△CDF为等边三角形.故选B.
11. A【解析】原式 n=p,∴原式=-1-1-1=-3.故选A.
12. B【解析】连接 CO.由题意可知AC=BC,∠ACB=90°,且点O 为AB的中点,∴CO⊥AB,∠DCO=∠BCO = 45°=∠EBO,∴CO=BO.∵∠DOE =∠COB=90°,∴∠COD+∠COE=∠COE+∠BOE,∴∠COD =∠BOE. 在△COD 和△BOE 中,
∴CD=BE,∴CE+CD=CE+BE=BC.在Rt△ABC中, 故选B.
13. x≠1 【解析】由题意得 x-1≠0,解得x≠1.
14.120°【解析】∵DE 平分∠CDA,AD∥BC,∴∠ADE=∠CED,∠ADE =∠CDE,∴∠CED=∠CDE,∴ CE= CD.∵BE:EC = 1:2,AB = CD,∴BE:AB=1:2.∵AE⊥BC,∴∠BAE=30°,∠B=60°,∴∠BCD=120°.
15.②③【解析】两班成绩的平均数相同,①错误;甲班成绩的方差比乙班成绩的方差大,故甲班成绩的波动比乙班成绩的波动大,②正确;③甲、乙两班参加人数相同,乙班成绩的中位数大于150次,甲班成绩的中位数小于150次,则甲班成绩优秀人数少于乙班成绩优秀人数,③正确.
16.m≤-1且m≠-2 【解析】去分母得2x-(x-1)=-m,解得x=-m-1.∵关于x的分式方程 的解为非负数,且x≠1,∴-m-1≥0且-m-1≠1,解得m≤-1且m≠-2.
17.1 【解析】如图,取 AC 的中点G,连接 BG,FG,则CG=CD.∵将线段 CE绕点C顺时针旋转60°得到 CF,∴CE=CF,∠ECF=60°.∵△ABC是等边三角形,∴∠ACB= 60°,∴∠DCE=∠ACF,∴ △CDE≌△CGF(SAS),∴∠FGC=∠EDC=90°,∴点F在直线 BG上运动.作DH⊥BG于点H,此时DF的最小值即为DH的值. 且易得∠CBG= 30°,故答案为1.
18.1500 【解析】设甲开始的速度为 a米/分,则甲后来的速度为 2a米/分.由题意可得 9+ 解得 a=500.设乙开始的速度为 b米/分.由甲、乙相遇知, 2a·1=(9-1)a,∴b=1000,∴甲、乙相遇时乙距公司的路程为 (米),甲到达小区所用时间为 (分),∴甲到小区时,乙距公司的路程为 1500(米),故答案为 1500.
19.【解】(1)原式=x -x+5x-5+x -4x+4=2x -1.
(2)原式=a (b-1)-b (b-1)=(b-1)(a -b )=(b-1)(a+b)(a-b).
(3)去分母,得4-(6x-2)= 3,去括号,得4-6x+2=3,解得 检验:当 时,6x-2≠0,∴分式方程的解为
20.【解】(1)原式
(2)原式
(3)原式 原式
21.【解】(1)如图所示,△A B C 即为所求.
(2)如图所示,△A B C 即为所求.
(3)如图所示,以O,A ,B为顶点的三角形为等腰直角三角形.
22.【解】(1)由表格及统计图中数据可知,实、虚线分别代表甲队、乙队,则甲队的平均数 86+95+91+96)= 90(分);甲队的方差是 [(82-90) +(86-90) +(95-90) +(91-90) +(96-90) ]=28.4;把乙队的成绩从小到大排列,中位数是87分.故答案为90,28.4,87.
(2)从平均数来看,甲、乙两队平均数相同;从方差来看,甲队方差小,乙队方差大,说明甲队成绩比较稳定;从获胜场数来看,甲队胜3场,乙队胜2场,说明甲队成绩较好.因此选派甲球队参赛更有可能取得好成绩.
23.(1)2 y轴 120°
(2)【解】由旋转得 OA=OD,∠AOD=120°.
∵△AOC是等边三角形,∴∠AOC=60°,∴∠COD=∠AOD-∠AOC=60°,∴∠COD=∠AOC.
又∵OA=OD,∴OC⊥AD,即∠AEO=90°.
24.【解】(1)设每套童装的原标价为x元.
根据题意,得 解得 x=200.
经检验,x=200是原方程的解,且符合题意.
答:每套童装的原标价为 200元.
(2)设该直播销售员每周需卖出这种童装 y套.
根据题意,得(200×0.9-150)y≥2700,解得y≥90.
答:该直播销售员每周至少需卖出这种童装90套.
25.【解】(1)当 t=2.5 时,四边形 ABQP 是平行四边形.理由:
∵四边形 ABCD 是平行四边形,∴AD∥BC,AB=CD=3c m,AD=BC=5cm,AO=CO,BO = OD,
∴∠PAO=∠QCO.在△APO 和△CQO中 ∴△APO≌△CQO(ASA),
∴AP=CQ=2.5cm .
∵BC=5cm ,∴BQ=5-2.5=2.5(cm),即 AP=BQ,AP∥BQ,∴四边形 ABQP 是平行四边形,即当
t=2.5时,四边形 ABQP 是平行四边形.
(2)如图,过A作AM⊥BC 于M,过O作ON⊥BC于 N.
∵AB⊥AC,AB=3c m,BC=5cm ,∴在 Rt△ABC中,由勾股定理得 AC=4 cm.∵由三角形的面积公式得 AM,∴AM= 2. 4 cm. ∵ BO 为△ABC 的中线, 即 ∵四边形 ABCD 是平行四边形,∴ 当t=4时,AP=CQ=4 cm,∴ △OQC 的面积为
2.4(cm ),∴y=3+2.4=5.4.
26.【解】(1)①∵∠AOB=150°,∠BOC=120°,
∴∠AOC=90°.由旋转的性质可知,∠OCD=60°,∠ADC=∠BOC=120°,
∴∠DAO=360°-60°-90°-120°=90°.
②线段 OA,OB,OC之间的数量关系是OA +OB =OC .证明如下:如图(1),连接OD.
∵△BOC绕点C按顺时针方向旋转60°得△ADC,∴△ADC≌△BOC,∠OCD=60°,∴CD=OC,∠ADC=∠BOC=120°,AD=OB,∴△OCD 是等边三角形,∴OC=OD=CD.
由①知∠DAO=90°,在 Rt△ADO中,OA +AD =OD ,∴OA +OB =OC .
(2)当α=β=120°时,OA+OB+OC 有最小值.理由如下:
如图(2),将△AOC 绕点 C 按顺时针方向旋转60°得 连接 是等边三角形, 点B,O,O',A'共线,. BA',此时OA+OB+OC 的值最小.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
五四制鲁教版数学八年级上册期末测试卷
一、选择题(本大题共36分,每小题3分)
1 . 2022年,中国航天迈着大步向浩瀚宇宙不断探索,神舟十四号载人飞船成功发射,世界首幅1:250 万月球全月地质图完成,我国首颗陆地生态系统碳监测卫星“句芒号”成功发射 下列航天图标,是中心对称图形的是( )
2.下列由左到右变形,属于因式分解且分解正确的是( )
3.若把x,y的值同时扩大为原来的2倍,则下列分式的值保持不变的是( )
4.若正多边形的内角和是1260°,则该正多边形的一个外角为( )
A.30° B.40° C.45° D.60°
5.某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是( )
A.甲种方案所用铁丝最长 B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长 D.三种方案所用铁丝一样长
6.四边形 ABCD中,对角线AC,BD相交于点O,给出下列四个条件:
①AD∥BC;②AD=BC;③OA=OC;④OB=OD.
从中任选两个条件能使四边形 ABCD为平行四边形的选法有( )
A.3种 B.4种 C.5种 D.6种
7.小明家1月至6月的用水量统计图如图所示,关于这组数据,下列说法错误的是( )
A.中位数是 5 吨 B.众数是6吨 C.平均数是 5吨 D.方差是
8.假期正是读书的好时候,小颖同学到重庆图书馆借了一本书,共280页,要在两周借期内读完,当她读了一半时,发现以后平均每天要多读21页才能在借期内读完,她读前一半时,平均每天读多少页 如果设读前一半时,平均每天读x页,则下面所列方程中,正确的是( )
9.如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE 是△ABC 的中位线,延长 DE 交△ABC
的外角∠ACM的平分线于点 F,则线段 DF的长为( )
A.7 B.8 C.9 D.10
第9题图 第10题图
10.如图,在平行四边形 ABCD中,∠B=60°,将△ABC沿AC 折叠,点 B的对应点落在点 E处,且点 B,A,E在一条直线上,CE交AD于点 F,则图中等边三角形共有( )
A.4个 B.3个 C.2个 D.1个
11.若 m+n-p=0,则 的值是( )
A.-3 B.-1 C.1 D.3
12.如图,在等腰直角三角形ABC中,∠C=90°,点O是AB的中点,且 将一块直角三角板的直角顶点放在点 O 处,将直角三角板绕点O 旋转,且在旋转过程中始终保持该直角三角板的两直角边分别与 AC,BC 相交,交点分别为点 D,E,则CD+CE=( )
A. C.2 D.
二、填空题(本大题共12分,每小题2分)
13.代数式 有意义时,x应满足的条件为_____________.
14 如图,在 ABCD中,点 E在 BC 边上,且AE⊥BC于点 E,DE 平分∠CDA.若 BE:EC=1:2,则∠BCD 的度数为____________.
15.某次跳绳比赛中,统计甲、乙两班学生每分钟跳绳的成绩(单位:次)情况如下表:
班级 参加人数 平均次数 中位数 方差
甲班 45 135 149 180
乙班 45 135 151 130
有下面三个命题:
①甲班平均成绩低于乙班平均成绩;
②甲班成绩的波动比乙班成绩的波动大;
③甲班成绩优秀人数少于乙班成绩优秀人数.(每分钟跳绳的成绩大于等于 150次为优秀).
其中正确的命题是_______________.(只填序号)
16.若关于x的分式方程 的解为非负数,则m的取值范围是__________.
17.如图,边长为4的等边三角形 ABC中,E是对称轴AD上的一个动点,连接 CE,将线段 CE 绕点C顺时针旋转60°得到CF,连接 DF,则在点 E运动过程中,DF的最小值是____________.
第17题图 第18题图
18.某快递公司快递员甲匀速骑车去距公司6000米的某小区取物件,出发几分钟后,该公司快递员乙发现甲的手机落在公司,于是立马匀速骑车去追赶甲,乙出发几分钟后,甲也发现自己的手机落在了公司,立即调头以原速的2倍原路返回,1分钟后遇到了乙,乙把手机给甲后,乙以原速的一半原路返回公司,甲以返回时的速度继续去小区取物件,刚好在事先预计的时间到达该小区.甲、乙两人相距的路程y(米)与甲出发的时间x(分)之间的关系如图所示(给手机及中途其他耽误时间忽略不计),则甲到小区时,乙距公司的路程是___________米.
三、解答题(本大题共72分.解答应写出文字说明、演算步骤或证明过程)
19.(6分)(1)计算:(x+5)·(x-1)+(x-2) .
(2)因式分解:a (b-1)+b -b .
(3)解方程:
20.(6分)(1)计算:
(2)计算:
(3)先化简 然后从-1,1,2三个数中任选一个合适的a代入求值.
21.(9分)如图,在平面直角坐标系中,已知△ABC 的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC 向下平移 5个单位得到△A B C ,请画出△A B C ;
(2)将△ABC 绕原点O 逆时针旋转90°后得到△A B C ,请画出△A B C ;
(3)判断以 O,A ,B为顶点的三角形的形状.(无需说明理由)
22.(9分)[2022山东烟台校级期中]甲、乙两支篮球队进行了5场比赛,将比赛成绩(整数)绘制成了折线统计图(实、虚线未标明球队)如下:
(1)填写下表:
平均数/分 中位数/分 方差
甲队 91
乙队 90 70.8
(2)如果从两队中选派一支球队参加篮球锦标赛,根据上述统计,从平均数、方差以及获胜场数这三个方面分别进行简要分析,你认为选派哪支球队参赛更有可能取得好成绩
23.(10分)如图,在平面直角坐标系xOy中,点A的坐标为(-2,0),等边三角形 AOC 经过平移或轴对称或旋转都可以得到△OBD.
(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是_______个单位长度;△AOC与△BOD关于某直线对称,则对称轴是________;△AOC 绕原点 O 顺时针旋转得到△DOB,则最小旋转角是__________.
(2)如图,连接AD,交 OC于点E,求∠AEO 的度数.
24.(10分)近年来,电商平台直播带货成了一个火热的新兴职业. 春节期间,某直播销售员销售一种童装.这种童装的进价为每套 150元,若按原标价销售,则每周销售额为10000 元;若按原标价的八五折销售,则每周多卖出20套,且销售额还增加1900元.
(1)求每套童装的原标价为多少元;
(2)若按原标价的九折销售,该直播销售员想要每周获利不低于 2700元,求该直播销售员每周至少需卖出这种童装多少套.
25.(10分)如图,在 ABCD中,对角线 AC,BD相交于点O,AB⊥AC,AB=3cm,BC=5cm .点P从 A 点出发沿 AD 方向匀速运动,速度为1 cm/s,连接 PO 并延长交 BC 于点 Q.设运动时间为 ts(0
(2)设四边形 OQCD 的面积为 y cm ,当t=4时,求y的值.
26.(12分)已知点 O 是等边△ABC 内的任意一点,连接 OA,OB,OC.
(1)如图所示,已知∠AOB=150°,∠BOC=120°,将△BOC绕点C按顺时针方向旋转60°得△ADC.
①求∠DAO的度数;
②猜想线段 OA,OB,OC之间的数量关系,并证明.
(2)设∠AOB=α,∠BOC=β.当α,β满足什么关系时,OA+OB+OC有最小值 并说明理由.
参考答案
1. B【解析】只有选项B能找到这样的一个点,使图形绕该点旋转180度后和原图形完全重合,所以是中心对称图形,故选B.
2. D 【解析】
A原变形是整式的乘法,不是因式分解,不符合题意;
B原变形错误,正确的是2x +4=2(x +2),不符合题意
C原变形错误,正确的是 不符合题意
D原变形符合因式分解的定义,且分解正确,符合题意
3. A【解析】 故选项 A的值保持不变. 故选项B的值不能保持不变.故选项 C的值不能保持不变. 故选项D的值不能保持不变.故选 A.
4. B【解析】设该正多边形的边数为 n.根据题意,得(n-2)·180°=1260°,解得 n=9,∴该正多边形的边数是9.∵多边形的外角和为360°,360°÷9=40°,∴该正多边形的一个外角为40°.故选B.
5. D【解析】题图中三个图形通过平移线段都可以得到边长分别为 a,b的长方形,所以其周长相等,所以三种方案用的铁丝的长度一样.
6. B【解析】从四个中任选两个,共有6种情况,具体如下表:
条件 四边形 ABCD是否为平行四边形
①② 是
①③ 是
①④ 是
②③ 否
②④ 否
③④ 是
7. A【解析】A 选项,这组数据按照从小到大的顺序排列为3,4,5,6,6,6,则这组数据的中位数是(5+6)÷2=5.5(吨),原来的说法错误,符合题意;B选项,众数是6吨,是正确的,不符合题意;C 选项,平均数为(4+6+3+5+6+6)÷6=(5)吨,是正确的,不符合题意;D选项,方差是 是正确的,不符合题意.故选A.
8. C【解析】读前一半用的时间为 天,读后一半用的时间为 天.由题意得, 故选C.
9. B【解析】∵∠ABC=90°,DE 是△ABC的中位线,AB=8,BC=6,∴DE 平行且等于 BC,AC=10,∴DE=3,CE = 5,∠FCM =∠CFE. ∵CF 平分∠ACM,∴∠ECF=∠FCM,∴∠ECF=∠CFE,∴EF=CE=5,∴DF=DE+EF=3+5=8.故选B.
10. B【解析】∵∠B=60°,将△ABC沿AC折叠,点B落在点E处,且点B,A,E在一条直线上,∴△BCE为等边三角形.∵AD∥BC,AB∥CD,易得△AEF和△CDF为等边三角形.故选B.
11. A【解析】原式 n=p,∴原式=-1-1-1=-3.故选A.
12. B【解析】连接 CO.由题意可知AC=BC,∠ACB=90°,且点O 为AB的中点,∴CO⊥AB,∠DCO=∠BCO = 45°=∠EBO,∴CO=BO.∵∠DOE =∠COB=90°,∴∠COD+∠COE=∠COE+∠BOE,∴∠COD =∠BOE. 在△COD 和△BOE 中,
∴CD=BE,∴CE+CD=CE+BE=BC.在Rt△ABC中, 故选B.
13. x≠1 【解析】由题意得 x-1≠0,解得x≠1.
14.120°【解析】∵DE 平分∠CDA,AD∥BC,∴∠ADE=∠CED,∠ADE =∠CDE,∴∠CED=∠CDE,∴ CE= CD.∵BE:EC = 1:2,AB = CD,∴BE:AB=1:2.∵AE⊥BC,∴∠BAE=30°,∠B=60°,∴∠BCD=120°.
15.②③【解析】两班成绩的平均数相同,①错误;甲班成绩的方差比乙班成绩的方差大,故甲班成绩的波动比乙班成绩的波动大,②正确;③甲、乙两班参加人数相同,乙班成绩的中位数大于150次,甲班成绩的中位数小于150次,则甲班成绩优秀人数少于乙班成绩优秀人数,③正确.
16.m≤-1且m≠-2 【解析】去分母得2x-(x-1)=-m,解得x=-m-1.∵关于x的分式方程 的解为非负数,且x≠1,∴-m-1≥0且-m-1≠1,解得m≤-1且m≠-2.
17.1 【解析】如图,取 AC 的中点G,连接 BG,FG,则CG=CD.∵将线段 CE绕点C顺时针旋转60°得到 CF,∴CE=CF,∠ECF=60°.∵△ABC是等边三角形,∴∠ACB= 60°,∴∠DCE=∠ACF,∴ △CDE≌△CGF(SAS),∴∠FGC=∠EDC=90°,∴点F在直线 BG上运动.作DH⊥BG于点H,此时DF的最小值即为DH的值. 且易得∠CBG= 30°,故答案为1.
18.1500 【解析】设甲开始的速度为 a米/分,则甲后来的速度为 2a米/分.由题意可得 9+ 解得 a=500.设乙开始的速度为 b米/分.由甲、乙相遇知, 2a·1=(9-1)a,∴b=1000,∴甲、乙相遇时乙距公司的路程为 (米),甲到达小区所用时间为 (分),∴甲到小区时,乙距公司的路程为 1500(米),故答案为 1500.
19.【解】(1)原式=x -x+5x-5+x -4x+4=2x -1.
(2)原式=a (b-1)-b (b-1)=(b-1)(a -b )=(b-1)(a+b)(a-b).
(3)去分母,得4-(6x-2)= 3,去括号,得4-6x+2=3,解得 检验:当 时,6x-2≠0,∴分式方程的解为
20.【解】(1)原式
(2)原式
(3)原式 原式
21.【解】(1)如图所示,△A B C 即为所求.
(2)如图所示,△A B C 即为所求.
(3)如图所示,以O,A ,B为顶点的三角形为等腰直角三角形.
22.【解】(1)由表格及统计图中数据可知,实、虚线分别代表甲队、乙队,则甲队的平均数 86+95+91+96)= 90(分);甲队的方差是 [(82-90) +(86-90) +(95-90) +(91-90) +(96-90) ]=28.4;把乙队的成绩从小到大排列,中位数是87分.故答案为90,28.4,87.
(2)从平均数来看,甲、乙两队平均数相同;从方差来看,甲队方差小,乙队方差大,说明甲队成绩比较稳定;从获胜场数来看,甲队胜3场,乙队胜2场,说明甲队成绩较好.因此选派甲球队参赛更有可能取得好成绩.
23.(1)2 y轴 120°
(2)【解】由旋转得 OA=OD,∠AOD=120°.
∵△AOC是等边三角形,∴∠AOC=60°,∴∠COD=∠AOD-∠AOC=60°,∴∠COD=∠AOC.
又∵OA=OD,∴OC⊥AD,即∠AEO=90°.
24.【解】(1)设每套童装的原标价为x元.
根据题意,得 解得 x=200.
经检验,x=200是原方程的解,且符合题意.
答:每套童装的原标价为 200元.
(2)设该直播销售员每周需卖出这种童装 y套.
根据题意,得(200×0.9-150)y≥2700,解得y≥90.
答:该直播销售员每周至少需卖出这种童装90套.
25.【解】(1)当 t=2.5 时,四边形 ABQP 是平行四边形.理由:
∵四边形 ABCD 是平行四边形,∴AD∥BC,AB=CD=3c m,AD=BC=5cm,AO=CO,BO = OD,
∴∠PAO=∠QCO.在△APO 和△CQO中 ∴△APO≌△CQO(ASA),
∴AP=CQ=2.5cm .
∵BC=5cm ,∴BQ=5-2.5=2.5(cm),即 AP=BQ,AP∥BQ,∴四边形 ABQP 是平行四边形,即当
t=2.5时,四边形 ABQP 是平行四边形.
(2)如图,过A作AM⊥BC 于M,过O作ON⊥BC于 N.
∵AB⊥AC,AB=3c m,BC=5cm ,∴在 Rt△ABC中,由勾股定理得 AC=4 cm.∵由三角形的面积公式得 AM,∴AM= 2. 4 cm. ∵ BO 为△ABC 的中线, 即 ∵四边形 ABCD 是平行四边形,∴ 当t=4时,AP=CQ=4 cm,∴ △OQC 的面积为
2.4(cm ),∴y=3+2.4=5.4.
26.【解】(1)①∵∠AOB=150°,∠BOC=120°,
∴∠AOC=90°.由旋转的性质可知,∠OCD=60°,∠ADC=∠BOC=120°,
∴∠DAO=360°-60°-90°-120°=90°.
②线段 OA,OB,OC之间的数量关系是OA +OB =OC .证明如下:如图(1),连接OD.
∵△BOC绕点C按顺时针方向旋转60°得△ADC,∴△ADC≌△BOC,∠OCD=60°,∴CD=OC,∠ADC=∠BOC=120°,AD=OB,∴△OCD 是等边三角形,∴OC=OD=CD.
由①知∠DAO=90°,在 Rt△ADO中,OA +AD =OD ,∴OA +OB =OC .
(2)当α=β=120°时,OA+OB+OC 有最小值.理由如下:
如图(2),将△AOC 绕点 C 按顺时针方向旋转60°得 连接 是等边三角形, 点B,O,O',A'共线,. BA',此时OA+OB+OC 的值最小.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
