4.1整式提升练习(含答案)冀教版数学七年级上册
文档属性
| 名称 | 4.1整式提升练习(含答案)冀教版数学七年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 334.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-24 00:00:00 | ||
图片预览


文档简介
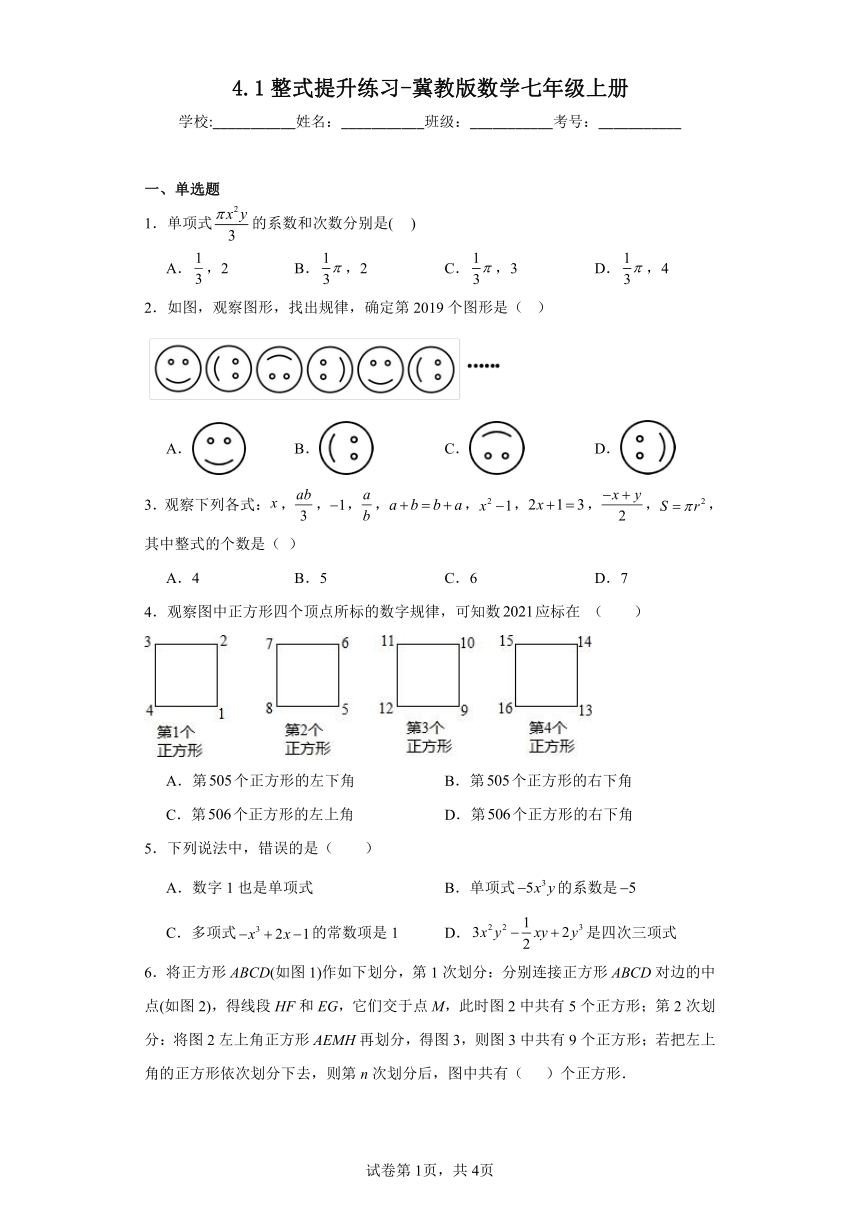
4.1整式提升练习-冀教版数学七年级上册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.单项式的系数和次数分别是( )
A.,2 B.,2 C.,3 D.,4
2.如图,观察图形,找出规律,确定第2019个图形是( )
A. B. C. D.
3.观察下列各式:,,,,,,,,,其中整式的个数是( )
A.4 B.5 C.6 D.7
4.观察图中正方形四个顶点所标的数字规律,可知数应标在 ( )
A.第个正方形的左下角 B.第个正方形的右下角
C.第个正方形的左上角 D.第个正方形的右下角
5.下列说法中,错误的是( )
A.数字1也是单项式 B.单项式的系数是
C.多项式的常数项是1 D.是四次三项式
6.将正方形ABCD(如图1)作如下划分,第1次划分:分别连接正方形ABCD对边的中点(如图2),得线段HF和EG,它们交于点M,此时图2中共有5个正方形;第2次划分:将图2左上角正方形AEMH再划分,得图3,则图3中共有9个正方形;若把左上角的正方形依次划分下去,则第n次划分后,图中共有( )个正方形.
A. B. C. D.
7.下列说法中,正确的是( )
A.不是整式 B.的系数是,次数是
C.是单项式 D.多项式的次数是
8.已知a=2,b=,则代数式的值是( )
A.0 B.1 C.3 D.4
9.已知整数…满足下列条件:, , ,,,…,,则的值为( )
A.-10 B.-50 C.-1009 D.-1005
10.单项式的系数和次数分别是( )
A., B., C., D.,
二、填空题
11.已知多项式kx2+4x﹣x2﹣5是关于x的一次多项式,则k= .
12.次数最高项是 ,项数是 ,常数项是 .
13.观察下列各式:1+1×3=22,1+2×4=32,1+3×5=42,…,第n个式子是 (n为正整数).
14.一列数、、、、…,按照如此规律第六个数应是 .
15.在图中每个小方格内填入一个数,使每一行、每一列都有1、2、3、4、5.那么,右下角的小方格(用粗线围出的方格)内填入的数应是 .
16.一个自然数的立方,可以分裂成若干个连续奇数的和,例如:23、33和43分别可以“分裂”成2个、3个和4个连续奇数的和,即23=3+5,33=7+9+11,43=13+15+17+19,…若1003也按照此规律来进行“分裂”,则1003“分裂”出的奇数中,最小的奇数是 .
17.观察下列算式31=3,32=9, 33=27,34=81,35=243,36=729,37=2187,38=6561 …… 则32011的末位数字是 .
18.考查下列式子,归纳规律并填空:
1=(-1)2×1;
1-3=(-1)3×2;
1-3+5=(-1)4×3;
… ……… … ……
1-3+5-7+…+(-1)(2n-1)= (n≥1且为整数).
19.按一定规律排列的一列数依次为,,,,,…,按此规律排列下去,这列数的第n个数是 .(n是正整数)
20.四个小朋友站成一排,老师按图中所示的规则数数,数到2015时对应的小朋友可得一朵红花.那么,得红花的小朋友是
三、解答题
21.阅读下文,寻找规律:
已知时, ,,…
(1)填空: .
(2)观察上式,并猜想:
①______.
②_________.
(3)根据你的猜想,计算:
①______.
②的值.
22.定义:a是不为1的有理数,我们把称为a的差倒数.如:2的差倒数是= 1,-1的差倒数是=.已知a1=,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数.
(1)计算:a2=__________,a3=__________.
(2)这列数有什么规律?根据你发现的规律计算a2015的值.
23.观察下面三行数:
-2,4,-8,16,-32,64,…;①
-1,5,-9,13,-17,21,…;②
-1,4,-9,16,-25,36,….③
(1)第①行第十个数是_______;
(2)第②行第十个数是________;
(3)取每行数的第十个数,计算这三个数的和是_________.
24.老师在黑板上写了三个算式,请同学们认真观察,发现规律,并结合这些算式解答下列问题.
请观察以下算式:①;②;③;……
(1)请结合上达三个算式的规律 ,写出第④个算式:______;
(2)写出你猜想的第n个等式(用含n的式子表示),并验证其正确性.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
2.C
3.B
4.D
5.C
6.C
7.C
8.D
9.C
10.C
11.1.
12. 4
13.
14.
15.3
16.9901
17.7
18.
19.
20.小李
21.(1)
(2)①;②
(3)①;②.
22.(1),;(2)规律:这列数每三个循环一次;a2015=.
23.(1)1024;(2)37;(3)1161
24.(1)
(2)
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.单项式的系数和次数分别是( )
A.,2 B.,2 C.,3 D.,4
2.如图,观察图形,找出规律,确定第2019个图形是( )
A. B. C. D.
3.观察下列各式:,,,,,,,,,其中整式的个数是( )
A.4 B.5 C.6 D.7
4.观察图中正方形四个顶点所标的数字规律,可知数应标在 ( )
A.第个正方形的左下角 B.第个正方形的右下角
C.第个正方形的左上角 D.第个正方形的右下角
5.下列说法中,错误的是( )
A.数字1也是单项式 B.单项式的系数是
C.多项式的常数项是1 D.是四次三项式
6.将正方形ABCD(如图1)作如下划分,第1次划分:分别连接正方形ABCD对边的中点(如图2),得线段HF和EG,它们交于点M,此时图2中共有5个正方形;第2次划分:将图2左上角正方形AEMH再划分,得图3,则图3中共有9个正方形;若把左上角的正方形依次划分下去,则第n次划分后,图中共有( )个正方形.
A. B. C. D.
7.下列说法中,正确的是( )
A.不是整式 B.的系数是,次数是
C.是单项式 D.多项式的次数是
8.已知a=2,b=,则代数式的值是( )
A.0 B.1 C.3 D.4
9.已知整数…满足下列条件:, , ,,,…,,则的值为( )
A.-10 B.-50 C.-1009 D.-1005
10.单项式的系数和次数分别是( )
A., B., C., D.,
二、填空题
11.已知多项式kx2+4x﹣x2﹣5是关于x的一次多项式,则k= .
12.次数最高项是 ,项数是 ,常数项是 .
13.观察下列各式:1+1×3=22,1+2×4=32,1+3×5=42,…,第n个式子是 (n为正整数).
14.一列数、、、、…,按照如此规律第六个数应是 .
15.在图中每个小方格内填入一个数,使每一行、每一列都有1、2、3、4、5.那么,右下角的小方格(用粗线围出的方格)内填入的数应是 .
16.一个自然数的立方,可以分裂成若干个连续奇数的和,例如:23、33和43分别可以“分裂”成2个、3个和4个连续奇数的和,即23=3+5,33=7+9+11,43=13+15+17+19,…若1003也按照此规律来进行“分裂”,则1003“分裂”出的奇数中,最小的奇数是 .
17.观察下列算式31=3,32=9, 33=27,34=81,35=243,36=729,37=2187,38=6561 …… 则32011的末位数字是 .
18.考查下列式子,归纳规律并填空:
1=(-1)2×1;
1-3=(-1)3×2;
1-3+5=(-1)4×3;
… ……… … ……
1-3+5-7+…+(-1)(2n-1)= (n≥1且为整数).
19.按一定规律排列的一列数依次为,,,,,…,按此规律排列下去,这列数的第n个数是 .(n是正整数)
20.四个小朋友站成一排,老师按图中所示的规则数数,数到2015时对应的小朋友可得一朵红花.那么,得红花的小朋友是
三、解答题
21.阅读下文,寻找规律:
已知时, ,,…
(1)填空: .
(2)观察上式,并猜想:
①______.
②_________.
(3)根据你的猜想,计算:
①______.
②的值.
22.定义:a是不为1的有理数,我们把称为a的差倒数.如:2的差倒数是= 1,-1的差倒数是=.已知a1=,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数.
(1)计算:a2=__________,a3=__________.
(2)这列数有什么规律?根据你发现的规律计算a2015的值.
23.观察下面三行数:
-2,4,-8,16,-32,64,…;①
-1,5,-9,13,-17,21,…;②
-1,4,-9,16,-25,36,….③
(1)第①行第十个数是_______;
(2)第②行第十个数是________;
(3)取每行数的第十个数,计算这三个数的和是_________.
24.老师在黑板上写了三个算式,请同学们认真观察,发现规律,并结合这些算式解答下列问题.
请观察以下算式:①;②;③;……
(1)请结合上达三个算式的规律 ,写出第④个算式:______;
(2)写出你猜想的第n个等式(用含n的式子表示),并验证其正确性.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
2.C
3.B
4.D
5.C
6.C
7.C
8.D
9.C
10.C
11.1.
12. 4
13.
14.
15.3
16.9901
17.7
18.
19.
20.小李
21.(1)
(2)①;②
(3)①;②.
22.(1),;(2)规律:这列数每三个循环一次;a2015=.
23.(1)1024;(2)37;(3)1161
24.(1)
(2)
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
