1.1 回归分析的基本思想及其初步应用(2)(浙江省嘉兴市)
文档属性
| 名称 | 1.1 回归分析的基本思想及其初步应用(2)(浙江省嘉兴市) |  | |
| 格式 | rar | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-01-15 18:39:00 | ||
图片预览





文档简介
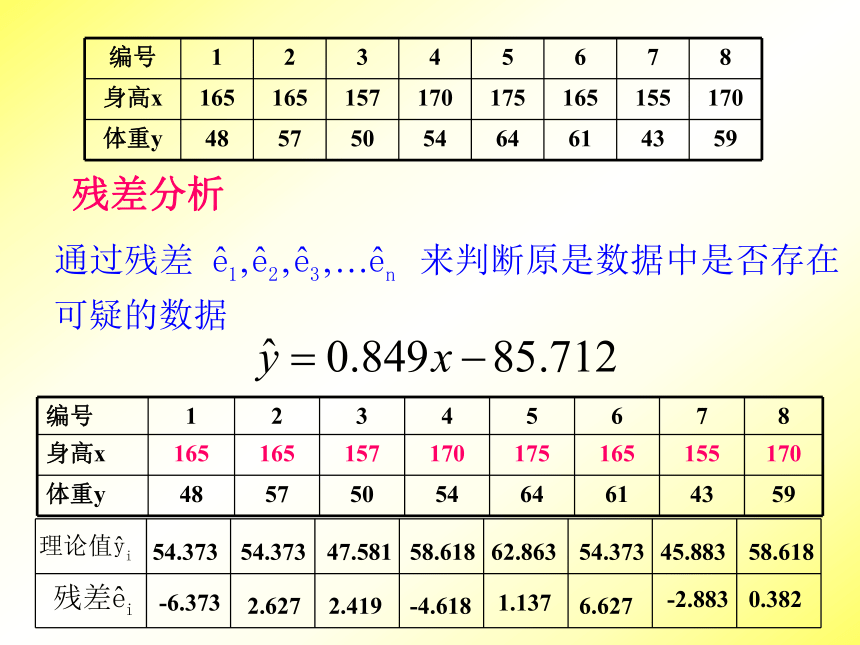
课件14张PPT。统计案例之回归方程表示解释变量(x)和 随机误差(e)的 总效应。 :表示随机误差的效应.(列表法)练:某种产品的广告费支出x与销售额y之间有如表所示数据:(1)求x,y之间的相关系数;
(2)求线性回归方程;
(3)求总偏差平方和及残差平方和;
(4)求R2,说明模型的拟合效果,残差变量对销售额的影响百分比.残差分析54.37354.37347.58158.61862.86354.37345.88358.618-6.3732.6272.419-4.6181.1376.627-2.8830.382-6.3732.6272.419-4.6181.1376.627-2.8830.382我们利用图形来分析残差特性,作图时纵坐标为残差,横坐
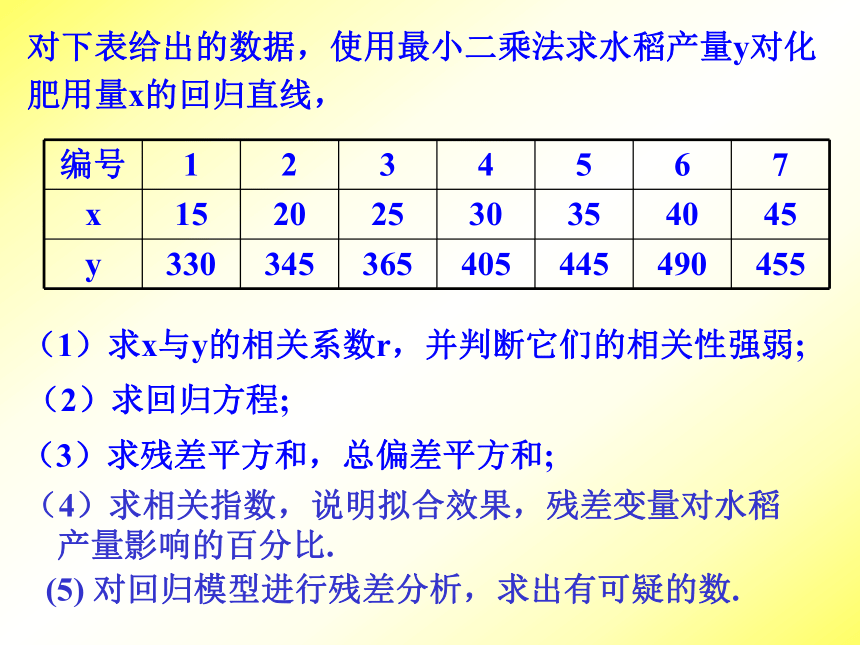
标可以选为样本编号、身高等,这样作出的图形叫做残差图可以看出第1个样本点和第6样本点的残差比较大,对下表给出的数据,使用最小二乘法求水稻产量y对化
肥用量x的回归直线,(1)求x与y的相关系数r,并判断它们的相关性强弱;(3)求残差平方和,总偏差平方和;(2)求回归方程;(4)求相关指数,说明拟合效果,残差变量对水稻产量影响的百分比. (5) 对回归模型进行残差分析,求出有可疑的数. 一只红铃虫的产卵数y和温度x有关,现收集了7组数据,试建立y与x的回归方程(1)收集数据,作散点图。 求y,关键求a,b 两边取自然对数,得 回归方程1.9462.3983.0453.1784.1904.7455.784方法:把非线性的回归问题化为线性问题来考虑,
通过变换来实现。(1)根据数据,作散点图 ;(2)由经验确定回归方程的类型(如观察到数据呈
线性关系,则选用线性回归方程y=bx+a) ;(3)若呈指数关系,则设为练习:下表时1957年美国旧轿车价格的调查资料,今以x表示使用年限,y表示年均价格(1)画散点图,观察图形呈什么函数模型?
(2)求该变量间的是否有显著相关关系?
(3)求该模型回归方程.
(4)预测使用10年时,年均价格为多少?由散点图看出y与x呈指数关系7.8837.5727.3096.9916.6406.2886.1825.6705.420
(2)求线性回归方程;
(3)求总偏差平方和及残差平方和;
(4)求R2,说明模型的拟合效果,残差变量对销售额的影响百分比.残差分析54.37354.37347.58158.61862.86354.37345.88358.618-6.3732.6272.419-4.6181.1376.627-2.8830.382-6.3732.6272.419-4.6181.1376.627-2.8830.382我们利用图形来分析残差特性,作图时纵坐标为残差,横坐
标可以选为样本编号、身高等,这样作出的图形叫做残差图可以看出第1个样本点和第6样本点的残差比较大,对下表给出的数据,使用最小二乘法求水稻产量y对化
肥用量x的回归直线,(1)求x与y的相关系数r,并判断它们的相关性强弱;(3)求残差平方和,总偏差平方和;(2)求回归方程;(4)求相关指数,说明拟合效果,残差变量对水稻产量影响的百分比. (5) 对回归模型进行残差分析,求出有可疑的数. 一只红铃虫的产卵数y和温度x有关,现收集了7组数据,试建立y与x的回归方程(1)收集数据,作散点图。 求y,关键求a,b 两边取自然对数,得 回归方程1.9462.3983.0453.1784.1904.7455.784方法:把非线性的回归问题化为线性问题来考虑,
通过变换来实现。(1)根据数据,作散点图 ;(2)由经验确定回归方程的类型(如观察到数据呈
线性关系,则选用线性回归方程y=bx+a) ;(3)若呈指数关系,则设为练习:下表时1957年美国旧轿车价格的调查资料,今以x表示使用年限,y表示年均价格(1)画散点图,观察图形呈什么函数模型?
(2)求该变量间的是否有显著相关关系?
(3)求该模型回归方程.
(4)预测使用10年时,年均价格为多少?由散点图看出y与x呈指数关系7.8837.5727.3096.9916.6406.2886.1825.6705.420
