第二十二章 二次函数 基础知识测试题(含解析)
文档属性
| 名称 | 第二十二章 二次函数 基础知识测试题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-25 10:19:52 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十二章 二次函数基础知识测试题
一、单选题
1.抛物线
与
轴的交点坐标为( )
A.
B.
C.
D.
2.一元二次方程3x2-2x-1=0的二次项系数、一次项系数、常数项分别为( ).
A.3,2,1 B.-3,2,1 C.3,-2,-1 D.-3,-2,-1
3.下列关系式中,属于二次函数的是(x为自变量)( ).
A. B. C. D.
4.在下列函数表达式中,一定为二次函数的是( )
A.y=x+3 B.y=ax2+bx+c C.y=t2-2t+2 D.y=x2+
5.下列各式中,y是x的二次函数的是( )
A. B. C. D.
6.将抛物线y=2(x﹣4)2﹣1先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线的解析式为( )
A.y=2x2+1 B.y=2x2﹣3
C.y=2(x﹣8)2+1 D.y=2(x﹣8)2﹣3
7.如图,水平线l1∥l2,铅垂线l3∥l4,l1⊥l3,若选择l1、l2其中一条当成x轴,且向右为正方向,再选择l3、l4其中一条当成y轴,且向上为正方向,并在此平面直角坐标系中画出二次函数y=ax2﹣ax﹣a的图象,则下列关于x、y轴的叙述,正确的是( )
A.l1为x轴,l3为y轴 B.l1为x轴,l4为y轴
C.l2为x轴,l3为y轴 D.l2为x轴,l4为y轴
8.已知抛物线,,,是抛物线上三点,则,,由小到大序排列是( )
A. B. C. D.
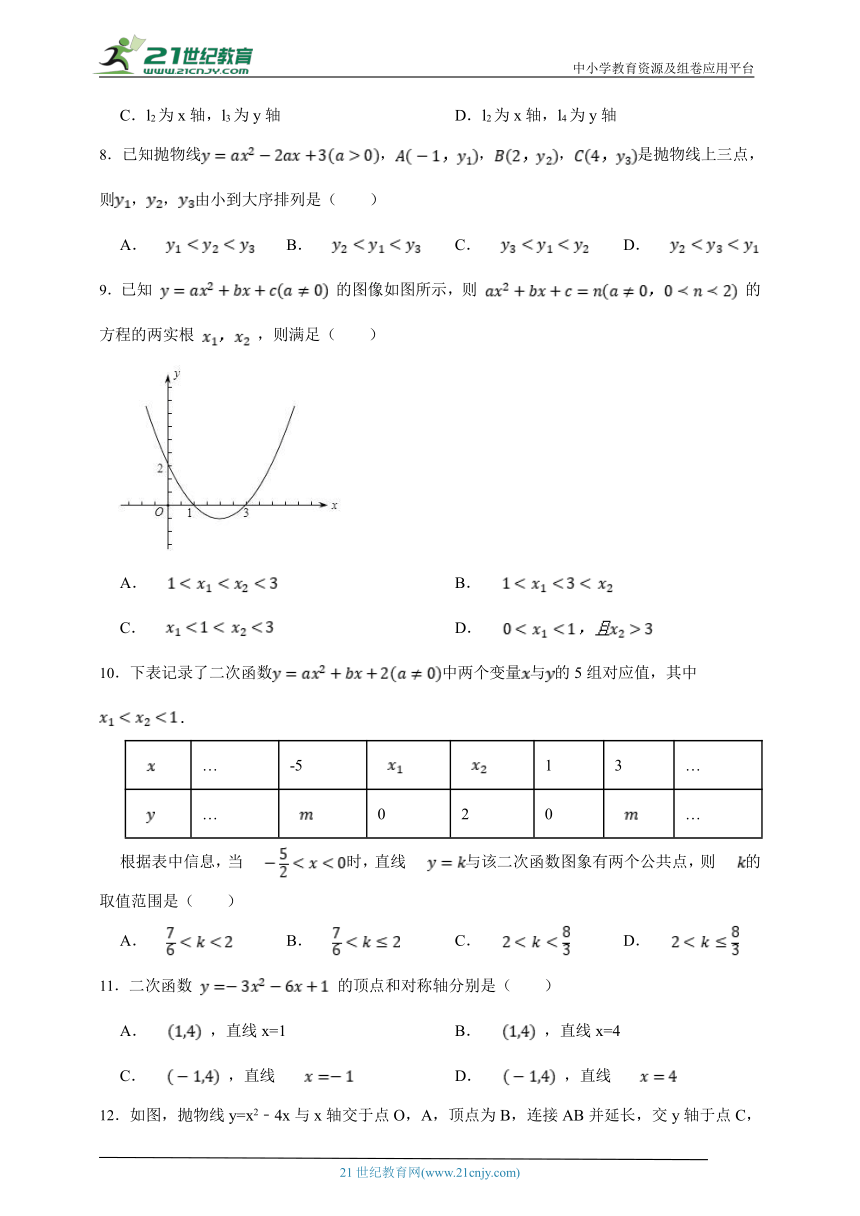
9.已知 的图像如图所示,则 的方程的两实根 ,则满足( )
A. B.
C. D.
10.下表记录了二次函数中两个变量与的5组对应值,其中.
… -5 1 3 …
… 0 2 0 …
根据表中信息,当时,直线与该二次函数图象有两个公共点,则的取值范围是( )
A. B. C. D.
11.二次函数 的顶点和对称轴分别是( )
A. ,直线x=1 B. ,直线x=4
C. ,直线 D. ,直线
12.如图,抛物线y=x2﹣4x与x轴交于点O,A,顶点为B,连接AB并延长,交y轴于点C,则图中阴影部分的面积和为( )
A.4 B.8 C.16 D.32
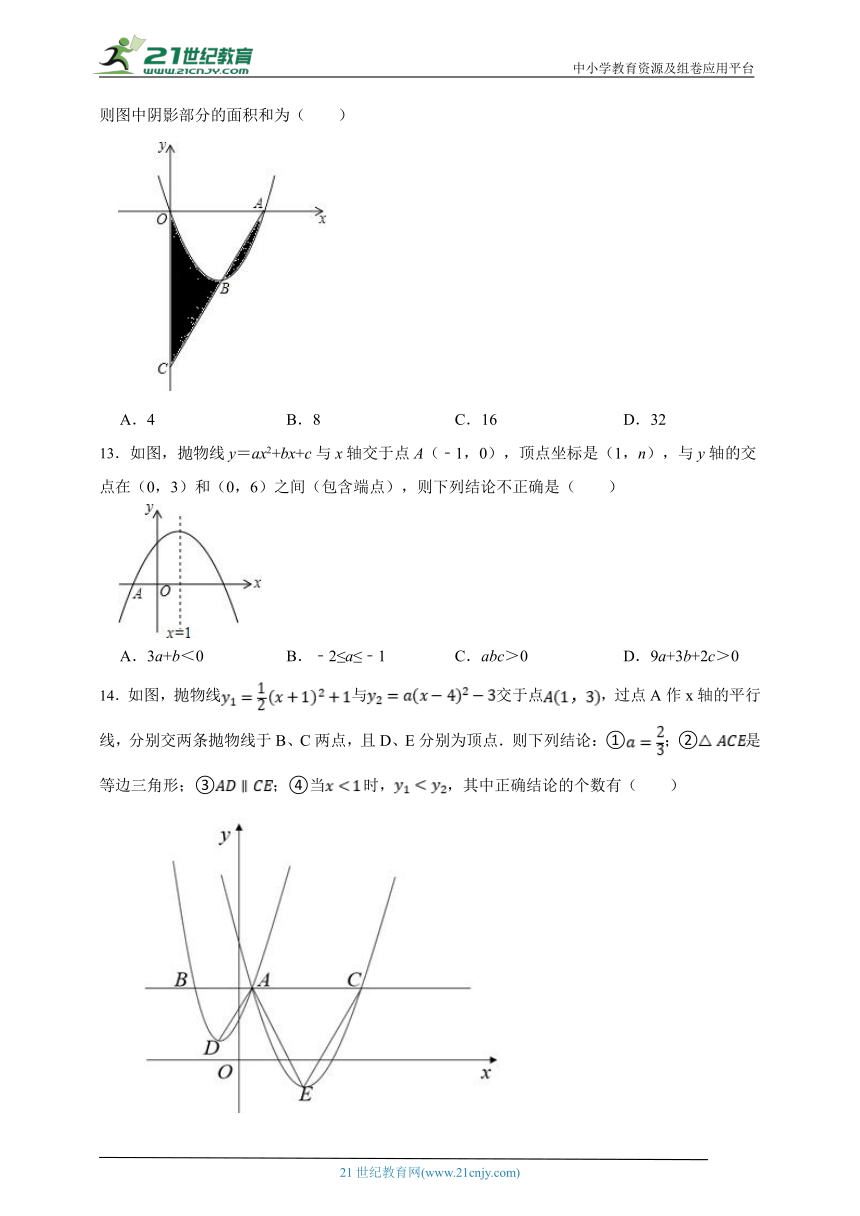
13.如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标是(1,n),与y轴的交点在(0,3)和(0,6)之间(包含端点),则下列结论不正确是( )
A.3a+b<0 B.﹣2≤a≤﹣1 C.abc>0 D.9a+3b+2c>0
14.如图,抛物线与交于点,过点A作x轴的平行线,分别交两条抛物线于B、C两点,且D、E分别为顶点.则下列结论:①;②是等边三角形;③;④当时,,其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
15.已知二次函数 的图象如图所示,有下列4个结论:
① ;② ;③ ;④ ;⑤2c<3b
其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
二、填空题
16.将抛物线 向右平移2个单位长度,再向上平移1个单位长度,所得抛物线的函数表达式是 .
17.抛物线 与直线 交于(1, ),则 = ;抛物线的解析式为
三、计算题
18. 计算题
(1)解方程:2x2﹣4x﹣6=0.
(2)①直接写出函数y=2x2﹣4x﹣6的图象与x轴交点坐标;
②求函数y=2x2﹣4x﹣6的图象的顶点坐标.
四、解答题
19.已知二次函数y=k(x+1)(x﹣)的图象与x轴交于点A,B,与y轴交于点C.
(1)写出点C的坐标;
(2)若△ABC为等腰三角形,求k的值.
五、作图题
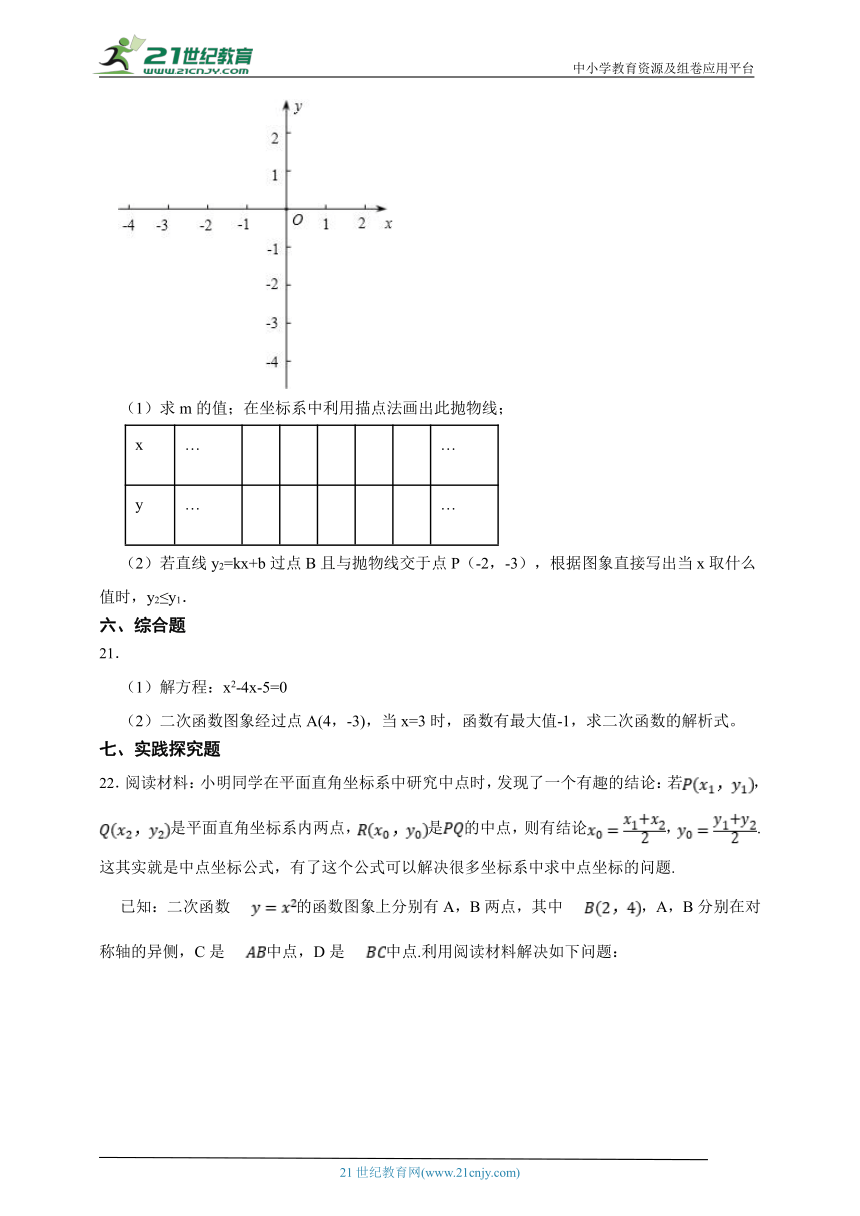
20.已知抛物线y1=x2+2(m+2)x+m-2与x轴交于A,B两点(点A在点B左侧),对称轴为直线x=-1.
(1)求m的值;在坐标系中利用描点法画出此抛物线;
x … …
y … …
(2)若直线y2=kx+b过点B且与抛物线交于点P(-2,-3),根据图象直接写出当x取什么值时,y2≤y1.
六、综合题
21.
(1)解方程:x2-4x-5=0
(2)二次函数图象经过点A(4,-3),当x=3时,函数有最大值-1,求二次函数的解析式。
七、实践探究题
22.阅读材料:小明同学在平面直角坐标系中研究中点时,发现了一个有趣的结论:若,是平面直角坐标系内两点,是的中点,则有结论,.这其实就是中点坐标公式,有了这个公式可以解决很多坐标系中求中点坐标的问题.
已知:二次函数的函数图象上分别有A,B两点,其中,A,B分别在对称轴的异侧,C是中点,D是中点.利用阅读材料解决如下问题:
(1) 概念理解:
如图1,若,求出C,D的坐标.
(2) 解决问题:
如图2,点A是B关于y轴的对称点,作轴交抛物线于点E.延长至F,使得.试判断F是否在x轴上,并说明理由.
(3) 拓展探究:
如图3,是一个动点,作轴交抛物线于点E.延长至F,使得.
①令,试探究值是否为定值,若是,求出这个定值;若不是,请说明理由.
②在①条件下,y轴上一点,抛物线上任意一点H,连接,,直接写出的最小值.
答案解析部分
1.【答案】C
【解析】【解答】解:因为抛物线
与y轴交点的横坐标为
,所以
,即交点坐标为(0,7)
故答案为:C.
【分析】若函数图象与y轴相交,则x=0,因此将x=0代入函数解析式,可求出对应的y的值,即可求解.
2.【答案】C
【解析】【解答】观察数字因数,给出的方程二次项系数、一次项系数、常数项分别为3,-2,-1.
故答案为:C.
【分析】利用二次函数的解析式直接写出二次项系数、一次项系数、常数项。
3.【答案】D
【解析】【解答】解:A选项没说明a,b,c是常数,故A不是二次函数;
B选项等号右边不是整式,也不是二次函数;
C选项等号右边不是整式也不是二次函数;
D选项符合定义,故D选项所给关系式是二次函数.
故答案为:D.
【分析】我们把形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做二次函数,据此进行判断.
4.【答案】C
【解析】【解答】解:A、y=x+3此函数是一次函数,故A不符合题意;
B、y=ax2+bx+c,当a=0,b≠0时,此函数是一次函数,当a≠0时,此函数是二次函数,故B不符合题意
C、y=t2-2t+2,此函数是二次函数,故C符合题意;
D、,此函数不是二次函数,故D不符合题意;
故答案为:C.
【分析】利用二次函数的定义:形如y=ax2+bx+c=0(a,b,c是常数且a≠0)则y是x的二次函数,再对各选项逐一判断。
5.【答案】B
【解析】【解答】解:A. 是一次函数,不符合题意;
B. 是二次函数,符合题意;
C. 不是二次函数,不符合题意;
D. 含有分式,不是二次函数,不符合题意;
故答案为:B.
【分析】根据二次函数的定义逐项判定即可。
6.【答案】A
【解析】【详解】抛物线y=2(x-4)2-1先向左平移4个单位长度,得到的抛物线解析式为y=2(x-4+4)2-1,即y=2x2-1,再向上平移2个单位长度得到的抛物线解析式为y=2x2-1+2,即y=2x2+1;
故答案为:A
【分析】根据抛物线平移的规律:左右平移在h后左加右减,上下平移在k后上加下减即可求出.
7.【答案】A
【解析】【解答】解:∵抛物线的开口向上,
∴a>0,
∴﹣a<0,
∴抛物线与y轴的负半轴相交,
∴l1为x轴,l3为y轴.
故选A.
【分析】根据抛物线的开口向上,可得a>0,则﹣a<0,可确定l1为x轴,再根据左同右异的法则,可得出l3为y轴,即可得出答案.
8.【答案】B
9.【答案】D
【解析】【解答】根据题意画出图形,如图所示:
在图形中作出y=n(0<n<2),两交点的横坐标分别为x1,x2,
则0<x1<1,且x2>3.
故答案为:D.
【分析】根据题意知,方程ax2+bx+c=n ( a ≠ 0 , 0 n 2 ) 的两实根 x1 , x2分别代表了二次函数 y=ax2+bx+c( a ≠ 0 ) 和y=n(0<n<2)的图像的交点的x坐标,故画出大致图像,可直接判断出答案为D。
10.【答案】C
【解析】【解答】解:由可得抛物线对称轴,
又由以及对称轴可得,
,则设抛物线交点式为,
与对比可得,解得,
二次函数表达式为,
当时,;
当时,;
当时,,
,当时,直线y=k与该二次函数图象有两个公共点,
,
故答案为:C
【分析】先利用待定系数法求出二次函数解析式,再利用二次函数的性质求解即可。
11.【答案】C
【解析】【解答】解: ,
∴抛物线的顶点坐标为(-1,4),对称轴为x=-1.
故答案为:C.
【分析】将二次函数的一般式配方为顶点式,可求顶点坐标及对称轴.
12.【答案】B
【解析】【解答】解:当y=0时,x2﹣4x=0,解得x1=0,x2=4,则A(4,0),
∵y=x2﹣4x=(x﹣2)2﹣4,
∴B(2,﹣4),
设直线AB的解析式为y=kx+b,
把A(4,0),B(2,﹣4)代入得 ,解得 ,
∴直线AB的解析式为y=2x﹣8;
当x=0时,y=2x﹣8=﹣8,则C(0,﹣8),
∴图中阴影部分的面积和=S△OBC= ×8×2=8.
故选B.
【分析】先通过解方程x2﹣4x=0得到A(4,0),再把解析式配成顶点式得到B(2,﹣4),接着利用待定系数法求出直线AB的解析式为y=2x﹣8,则可得到C(0,﹣8),然后利用抛物线的对称性得到图中阴影部分的面积和=S△OBC,最后根据三角形面积公式求解.
13.【答案】C
【解析】【解答】解:A.根据图示知,抛物线开口方向向下,则a<0.
∵对称轴x= =1,
∴b=﹣2a,
∴3a+b=3a﹣2a=a<0,即3a+b<0.
故A不符合题意;
B.抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),对称轴直线是x=1,
∴该抛物线与x轴的另一个交点的坐标是(3,0),
∴﹣1×3=﹣3,
∴ =﹣3,则a=﹣ .
∵抛物线与y轴的交点在(0,3)、(0,6)之间(包含端点),
∴3≤c≤6,
∴﹣2≤﹣ ≤﹣1,即﹣2≤a≤﹣1.
故B不符合题意;
C.∵抛物线开口方向向下,则a<0,
∵与y轴的交点在(0,3)和(0,6)之间,则c>0,
∵对称轴直线是x=1,则a与b异号,即b>0,
∴abc<0,
故C符合题意;
D.∵则a=﹣ ,即c=﹣3a,b=﹣2a,
∴9a+3b+2c=9a+(﹣6a)+(﹣6a)=﹣3a,、
∵a<0,
∴9a+3b+2c=﹣3a>0
故D不符合题意,
故答案为:C
【分析】根据二次函数图象的性质进行判断即可.
14.【答案】B
【解析】【解答】将点代入可得:,
解得:,故①正确;
∵D、E分别为顶点,
∴,,
又∵过点A作x轴的平行线,分别交两条抛物线于B、C两点,
设,代入中可得:,
∴,
∴,
∴,
∴,故②错误;
设直线AD的解析式为,
∵,,
∴,解得:,
∴;
设直线CE的解析式为,
∵,,
∴,解得:,
∴;
∵,
∴AD与CE不平行,故③错误;
令,
解得:,,
∴当或时,,故④正确;
故正确的是①④;
故答案为:B.
【分析】将点代入y2中可求出a值,即可判断①;先分别求出顶点D、E的坐标,过点A作x轴的平行线,分别交两条抛物线于B、C两点,将y=3代入y2中求出x值,即得,然后分别求出AC、AE的长,即可判断②;利用待定系数法分求出直线AD、CE的解析式,根据“k相同,线平行”即可判断③;先令y1=y2求出x值,即得量抛物线交点的横坐标,利用图象可得时所对应的x范围,从而判断④.
15.【答案】B
【解析】【解答】解: ①∵图象的开口向下,∴a<0, 又∵图象与y轴的交点在y正半轴,∴c>0, ∵对称轴x==1, ∴b=-2a>0, ∴abc<0, 错误;
② 如图,当x=-1时,y=a-b+c<0, ∴b>a+c, 错误;
③ ∵,∴当x=0时y>0, 当x=2时,y=4a+2b+c>0,正确;
④ 当x=1时,y=a+b+c,函数有最大值,而x=m时,y=am2+bm+c,则a+b+c>am2+bm+c,
∴a+b>m(am+b),正确;
⑤当x=3时,y=9a+3b+c<0, 且x==2, 得a=-, 代入得9(-)+3b+c<0, 得2c<3b, 正确.
综上,正确的有3项.
故答案为:B.
【分析】由抛物线的开口方向判断a的符号,由抛物线与轴的交点判断c的符号,然后根据对称轴及抛物线与x轴的交点情况进行推理,进而对所得结论进行判断.
16.【答案】
【解析】【解答】解:抛物线 的顶点坐标为(0,0),再利用点的平移规律得到点(0,0)平移后对应的点的坐标为(2,1),所以平移后的抛物线解析式为: .
故答案为: .
【分析】利用平移规律“上加下减,左加右减”即可得到结论。
17.【答案】-1;y=-x2
【解析】【解答】解:根据题意,m=-1
抛物线y=ax2过(1,-1)
所以a=-1
抛物线的解析式为y=-x2.
故答案为:-1;y=-x2
【分析】根据点(1,m)在直线y=-x上可求得m的值,由题意将点(1, m )代入抛物线的解析式即可求得a的值。
18.【答案】(1)解:解方程2x2﹣4x﹣6=0,
整理得x2﹣2x﹣3=0,
(x﹣3)(x+1)=0,
x﹣3=0或x+1=0,
所以x1=3,x2=﹣1;
(2)解:①函数y=2x2﹣4x﹣6的图象与x轴交点坐标(3,0),(﹣1,0);
②y=2(x2﹣2x)﹣6
=2(x2﹣2x+1﹣1)﹣6
=2(x﹣1)2﹣8,
所以抛物线的顶点(1,﹣8).
【解析】【分析】(1)根据因式分解法求出x的值;(2)根据(1)中的解直接写出函数的图象与x轴交点坐标;由顶点式得到抛物线的顶点坐标.
19.【答案】解:(1)当x=0时,y=k(x+1)(x﹣)=k (﹣)=﹣3,
所以C点坐标为(0,﹣3);
(2)当y=0时,k(x+1)(x﹣)=0,解得x1=﹣1,x2=,
设A(﹣1,0),B(,0),
AC= =
若k>0,
当CA=CB,则OA=OB,即=1,解得k=3;
当AB=AC,解+1=,解得k= ;
当BA=BC时,即+1= ,解得k=;
若k<0时,AB=AC,即﹣1﹣=,解得k=﹣,
综上所述,k的值为3或或﹣或.
【解析】【分析】(1)计算自变量为0时的函数值即可得到C点坐标;
(2)先通过解方程k(x+1)(x﹣)=0得点A、B坐标,讨论:若k>0,当CA=CB,则OA=OB;当AB=AC;当BA=BC时;若k<0时,AB=AC,利用两点间的距离公式分别得到关于k的方程,然后解方程求出对应的k的值.
20.【答案】(1)解:抛物线对称轴为直线x=- =-1,
解得m=-1
函数解析式为y=x2+2x-3,
x … -3 -2 -1 0 1 …
y … 0 -3 -4 -3 0 …
(2)解:∵直线y2=kx+b过点B且与抛物线交于点P(-2,-3),
∴x<-2或x>1时,y2≤y1.
【解析】【分析】(1)由抛物线的对称轴x=1,可以求得m的值,取x与y的值分别填入表中,然后再描点,连线,画出函数的图象;
(2)由图可知,直线y2过点B(1,0)与P(-2,-3),利用待定系数法可以求得k与b的值,画出图像,即可写出y2≤y1时,x的取值。
21.【答案】(1)解:(x-5)(x+1)=0
x1=5,x2=1
(2)解:由题意可知此抛顶点坐标为(a,-1)
设其解析式为=a(x-3)2-1
将点(4,-3)代入得:-3=a-1
解得:a=-2
∴此抛物线解析式为y=-2(x-3)2-1
【解析】【分析】(1)根据解方程的步骤进行计算即可;
(2)根据题意,设出抛物线的解析式,根据待定系数法,得到答案即可。
22.【答案】(1)解:∵,,C是中点,
∴,,
;
,,D是中点
,,
;
(2)解:F是在x轴上,理由如下:
,点A是B关于y轴的对称点,
,
是中点,D是中点,
,则;
轴交抛物线于点,
,
把代入得,,,
,,
轴,且,
是在x轴上;
(3)解:①,,C是中点,
;
是中点,
;
轴交抛物线于点E,
,
把代入得,,
轴交抛物线于点E.延长至F,使得,
,,
,即,
,,
,
点在上,,
,
轴,,
即,,,
综上是一个定值;
②
【解析】【解答】解:(3)②∵是y轴上一点,H是抛物线上任意一点,,
∴当点G、H、F共线时,最小,最小值为的长度,
∵,
∴
,
∵,
∴当时,最小,最小值为,
此时,最小为,
故的最小值为.
【分析】(1)根据中点坐标公式进行解答;
(2)关于y轴对称的点:横坐标互为相反数,纵坐标相同,据此可得点A的坐标,由C是AB的中点,D是BC的中点可得点C、D的坐标,由DE∥y轴可得xE=xD=1,将xE=1代入抛物线解析式中求出yE,得到点E的坐标,然后求出DE、EF的值,据此解答;
(3)①根据中点坐标公式可得点C、D的坐标,由DE∥y轴可得xE=xD,将xE代入抛物线解析式中求出yE,表示出点E的坐标,然后表示出yF,根据点A(m,n)在抛物线上可得n=m2,据此解答;
②由题意可得:当点G、H、F共线时,GH+HF最小,最小值为GF的长度,根据勾股定理表示出GF2,然后根据二次函数的性质进行解答.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第二十二章 二次函数基础知识测试题
一、单选题
1.抛物线
与
轴的交点坐标为( )
A.
B.
C.
D.
2.一元二次方程3x2-2x-1=0的二次项系数、一次项系数、常数项分别为( ).
A.3,2,1 B.-3,2,1 C.3,-2,-1 D.-3,-2,-1
3.下列关系式中,属于二次函数的是(x为自变量)( ).
A. B. C. D.
4.在下列函数表达式中,一定为二次函数的是( )
A.y=x+3 B.y=ax2+bx+c C.y=t2-2t+2 D.y=x2+
5.下列各式中,y是x的二次函数的是( )
A. B. C. D.
6.将抛物线y=2(x﹣4)2﹣1先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线的解析式为( )
A.y=2x2+1 B.y=2x2﹣3
C.y=2(x﹣8)2+1 D.y=2(x﹣8)2﹣3
7.如图,水平线l1∥l2,铅垂线l3∥l4,l1⊥l3,若选择l1、l2其中一条当成x轴,且向右为正方向,再选择l3、l4其中一条当成y轴,且向上为正方向,并在此平面直角坐标系中画出二次函数y=ax2﹣ax﹣a的图象,则下列关于x、y轴的叙述,正确的是( )
A.l1为x轴,l3为y轴 B.l1为x轴,l4为y轴
C.l2为x轴,l3为y轴 D.l2为x轴,l4为y轴
8.已知抛物线,,,是抛物线上三点,则,,由小到大序排列是( )
A. B. C. D.
9.已知 的图像如图所示,则 的方程的两实根 ,则满足( )
A. B.
C. D.
10.下表记录了二次函数中两个变量与的5组对应值,其中.
… -5 1 3 …
… 0 2 0 …
根据表中信息,当时,直线与该二次函数图象有两个公共点,则的取值范围是( )
A. B. C. D.
11.二次函数 的顶点和对称轴分别是( )
A. ,直线x=1 B. ,直线x=4
C. ,直线 D. ,直线
12.如图,抛物线y=x2﹣4x与x轴交于点O,A,顶点为B,连接AB并延长,交y轴于点C,则图中阴影部分的面积和为( )
A.4 B.8 C.16 D.32
13.如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标是(1,n),与y轴的交点在(0,3)和(0,6)之间(包含端点),则下列结论不正确是( )
A.3a+b<0 B.﹣2≤a≤﹣1 C.abc>0 D.9a+3b+2c>0
14.如图,抛物线与交于点,过点A作x轴的平行线,分别交两条抛物线于B、C两点,且D、E分别为顶点.则下列结论:①;②是等边三角形;③;④当时,,其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
15.已知二次函数 的图象如图所示,有下列4个结论:
① ;② ;③ ;④ ;⑤2c<3b
其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
二、填空题
16.将抛物线 向右平移2个单位长度,再向上平移1个单位长度,所得抛物线的函数表达式是 .
17.抛物线 与直线 交于(1, ),则 = ;抛物线的解析式为
三、计算题
18. 计算题
(1)解方程:2x2﹣4x﹣6=0.
(2)①直接写出函数y=2x2﹣4x﹣6的图象与x轴交点坐标;
②求函数y=2x2﹣4x﹣6的图象的顶点坐标.
四、解答题
19.已知二次函数y=k(x+1)(x﹣)的图象与x轴交于点A,B,与y轴交于点C.
(1)写出点C的坐标;
(2)若△ABC为等腰三角形,求k的值.
五、作图题
20.已知抛物线y1=x2+2(m+2)x+m-2与x轴交于A,B两点(点A在点B左侧),对称轴为直线x=-1.
(1)求m的值;在坐标系中利用描点法画出此抛物线;
x … …
y … …
(2)若直线y2=kx+b过点B且与抛物线交于点P(-2,-3),根据图象直接写出当x取什么值时,y2≤y1.
六、综合题
21.
(1)解方程:x2-4x-5=0
(2)二次函数图象经过点A(4,-3),当x=3时,函数有最大值-1,求二次函数的解析式。
七、实践探究题
22.阅读材料:小明同学在平面直角坐标系中研究中点时,发现了一个有趣的结论:若,是平面直角坐标系内两点,是的中点,则有结论,.这其实就是中点坐标公式,有了这个公式可以解决很多坐标系中求中点坐标的问题.
已知:二次函数的函数图象上分别有A,B两点,其中,A,B分别在对称轴的异侧,C是中点,D是中点.利用阅读材料解决如下问题:
(1) 概念理解:
如图1,若,求出C,D的坐标.
(2) 解决问题:
如图2,点A是B关于y轴的对称点,作轴交抛物线于点E.延长至F,使得.试判断F是否在x轴上,并说明理由.
(3) 拓展探究:
如图3,是一个动点,作轴交抛物线于点E.延长至F,使得.
①令,试探究值是否为定值,若是,求出这个定值;若不是,请说明理由.
②在①条件下,y轴上一点,抛物线上任意一点H,连接,,直接写出的最小值.
答案解析部分
1.【答案】C
【解析】【解答】解:因为抛物线
与y轴交点的横坐标为
,所以
,即交点坐标为(0,7)
故答案为:C.
【分析】若函数图象与y轴相交,则x=0,因此将x=0代入函数解析式,可求出对应的y的值,即可求解.
2.【答案】C
【解析】【解答】观察数字因数,给出的方程二次项系数、一次项系数、常数项分别为3,-2,-1.
故答案为:C.
【分析】利用二次函数的解析式直接写出二次项系数、一次项系数、常数项。
3.【答案】D
【解析】【解答】解:A选项没说明a,b,c是常数,故A不是二次函数;
B选项等号右边不是整式,也不是二次函数;
C选项等号右边不是整式也不是二次函数;
D选项符合定义,故D选项所给关系式是二次函数.
故答案为:D.
【分析】我们把形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做二次函数,据此进行判断.
4.【答案】C
【解析】【解答】解:A、y=x+3此函数是一次函数,故A不符合题意;
B、y=ax2+bx+c,当a=0,b≠0时,此函数是一次函数,当a≠0时,此函数是二次函数,故B不符合题意
C、y=t2-2t+2,此函数是二次函数,故C符合题意;
D、,此函数不是二次函数,故D不符合题意;
故答案为:C.
【分析】利用二次函数的定义:形如y=ax2+bx+c=0(a,b,c是常数且a≠0)则y是x的二次函数,再对各选项逐一判断。
5.【答案】B
【解析】【解答】解:A. 是一次函数,不符合题意;
B. 是二次函数,符合题意;
C. 不是二次函数,不符合题意;
D. 含有分式,不是二次函数,不符合题意;
故答案为:B.
【分析】根据二次函数的定义逐项判定即可。
6.【答案】A
【解析】【详解】抛物线y=2(x-4)2-1先向左平移4个单位长度,得到的抛物线解析式为y=2(x-4+4)2-1,即y=2x2-1,再向上平移2个单位长度得到的抛物线解析式为y=2x2-1+2,即y=2x2+1;
故答案为:A
【分析】根据抛物线平移的规律:左右平移在h后左加右减,上下平移在k后上加下减即可求出.
7.【答案】A
【解析】【解答】解:∵抛物线的开口向上,
∴a>0,
∴﹣a<0,
∴抛物线与y轴的负半轴相交,
∴l1为x轴,l3为y轴.
故选A.
【分析】根据抛物线的开口向上,可得a>0,则﹣a<0,可确定l1为x轴,再根据左同右异的法则,可得出l3为y轴,即可得出答案.
8.【答案】B
9.【答案】D
【解析】【解答】根据题意画出图形,如图所示:
在图形中作出y=n(0<n<2),两交点的横坐标分别为x1,x2,
则0<x1<1,且x2>3.
故答案为:D.
【分析】根据题意知,方程ax2+bx+c=n ( a ≠ 0 , 0 n 2 ) 的两实根 x1 , x2分别代表了二次函数 y=ax2+bx+c( a ≠ 0 ) 和y=n(0<n<2)的图像的交点的x坐标,故画出大致图像,可直接判断出答案为D。
10.【答案】C
【解析】【解答】解:由可得抛物线对称轴,
又由以及对称轴可得,
,则设抛物线交点式为,
与对比可得,解得,
二次函数表达式为,
当时,;
当时,;
当时,,
,当时,直线y=k与该二次函数图象有两个公共点,
,
故答案为:C
【分析】先利用待定系数法求出二次函数解析式,再利用二次函数的性质求解即可。
11.【答案】C
【解析】【解答】解: ,
∴抛物线的顶点坐标为(-1,4),对称轴为x=-1.
故答案为:C.
【分析】将二次函数的一般式配方为顶点式,可求顶点坐标及对称轴.
12.【答案】B
【解析】【解答】解:当y=0时,x2﹣4x=0,解得x1=0,x2=4,则A(4,0),
∵y=x2﹣4x=(x﹣2)2﹣4,
∴B(2,﹣4),
设直线AB的解析式为y=kx+b,
把A(4,0),B(2,﹣4)代入得 ,解得 ,
∴直线AB的解析式为y=2x﹣8;
当x=0时,y=2x﹣8=﹣8,则C(0,﹣8),
∴图中阴影部分的面积和=S△OBC= ×8×2=8.
故选B.
【分析】先通过解方程x2﹣4x=0得到A(4,0),再把解析式配成顶点式得到B(2,﹣4),接着利用待定系数法求出直线AB的解析式为y=2x﹣8,则可得到C(0,﹣8),然后利用抛物线的对称性得到图中阴影部分的面积和=S△OBC,最后根据三角形面积公式求解.
13.【答案】C
【解析】【解答】解:A.根据图示知,抛物线开口方向向下,则a<0.
∵对称轴x= =1,
∴b=﹣2a,
∴3a+b=3a﹣2a=a<0,即3a+b<0.
故A不符合题意;
B.抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),对称轴直线是x=1,
∴该抛物线与x轴的另一个交点的坐标是(3,0),
∴﹣1×3=﹣3,
∴ =﹣3,则a=﹣ .
∵抛物线与y轴的交点在(0,3)、(0,6)之间(包含端点),
∴3≤c≤6,
∴﹣2≤﹣ ≤﹣1,即﹣2≤a≤﹣1.
故B不符合题意;
C.∵抛物线开口方向向下,则a<0,
∵与y轴的交点在(0,3)和(0,6)之间,则c>0,
∵对称轴直线是x=1,则a与b异号,即b>0,
∴abc<0,
故C符合题意;
D.∵则a=﹣ ,即c=﹣3a,b=﹣2a,
∴9a+3b+2c=9a+(﹣6a)+(﹣6a)=﹣3a,、
∵a<0,
∴9a+3b+2c=﹣3a>0
故D不符合题意,
故答案为:C
【分析】根据二次函数图象的性质进行判断即可.
14.【答案】B
【解析】【解答】将点代入可得:,
解得:,故①正确;
∵D、E分别为顶点,
∴,,
又∵过点A作x轴的平行线,分别交两条抛物线于B、C两点,
设,代入中可得:,
∴,
∴,
∴,
∴,故②错误;
设直线AD的解析式为,
∵,,
∴,解得:,
∴;
设直线CE的解析式为,
∵,,
∴,解得:,
∴;
∵,
∴AD与CE不平行,故③错误;
令,
解得:,,
∴当或时,,故④正确;
故正确的是①④;
故答案为:B.
【分析】将点代入y2中可求出a值,即可判断①;先分别求出顶点D、E的坐标,过点A作x轴的平行线,分别交两条抛物线于B、C两点,将y=3代入y2中求出x值,即得,然后分别求出AC、AE的长,即可判断②;利用待定系数法分求出直线AD、CE的解析式,根据“k相同,线平行”即可判断③;先令y1=y2求出x值,即得量抛物线交点的横坐标,利用图象可得时所对应的x范围,从而判断④.
15.【答案】B
【解析】【解答】解: ①∵图象的开口向下,∴a<0, 又∵图象与y轴的交点在y正半轴,∴c>0, ∵对称轴x==1, ∴b=-2a>0, ∴abc<0, 错误;
② 如图,当x=-1时,y=a-b+c<0, ∴b>a+c, 错误;
③ ∵,∴当x=0时y>0, 当x=2时,y=4a+2b+c>0,正确;
④ 当x=1时,y=a+b+c,函数有最大值,而x=m时,y=am2+bm+c,则a+b+c>am2+bm+c,
∴a+b>m(am+b),正确;
⑤当x=3时,y=9a+3b+c<0, 且x==2, 得a=-, 代入得9(-)+3b+c<0, 得2c<3b, 正确.
综上,正确的有3项.
故答案为:B.
【分析】由抛物线的开口方向判断a的符号,由抛物线与轴的交点判断c的符号,然后根据对称轴及抛物线与x轴的交点情况进行推理,进而对所得结论进行判断.
16.【答案】
【解析】【解答】解:抛物线 的顶点坐标为(0,0),再利用点的平移规律得到点(0,0)平移后对应的点的坐标为(2,1),所以平移后的抛物线解析式为: .
故答案为: .
【分析】利用平移规律“上加下减,左加右减”即可得到结论。
17.【答案】-1;y=-x2
【解析】【解答】解:根据题意,m=-1
抛物线y=ax2过(1,-1)
所以a=-1
抛物线的解析式为y=-x2.
故答案为:-1;y=-x2
【分析】根据点(1,m)在直线y=-x上可求得m的值,由题意将点(1, m )代入抛物线的解析式即可求得a的值。
18.【答案】(1)解:解方程2x2﹣4x﹣6=0,
整理得x2﹣2x﹣3=0,
(x﹣3)(x+1)=0,
x﹣3=0或x+1=0,
所以x1=3,x2=﹣1;
(2)解:①函数y=2x2﹣4x﹣6的图象与x轴交点坐标(3,0),(﹣1,0);
②y=2(x2﹣2x)﹣6
=2(x2﹣2x+1﹣1)﹣6
=2(x﹣1)2﹣8,
所以抛物线的顶点(1,﹣8).
【解析】【分析】(1)根据因式分解法求出x的值;(2)根据(1)中的解直接写出函数的图象与x轴交点坐标;由顶点式得到抛物线的顶点坐标.
19.【答案】解:(1)当x=0时,y=k(x+1)(x﹣)=k (﹣)=﹣3,
所以C点坐标为(0,﹣3);
(2)当y=0时,k(x+1)(x﹣)=0,解得x1=﹣1,x2=,
设A(﹣1,0),B(,0),
AC= =
若k>0,
当CA=CB,则OA=OB,即=1,解得k=3;
当AB=AC,解+1=,解得k= ;
当BA=BC时,即+1= ,解得k=;
若k<0时,AB=AC,即﹣1﹣=,解得k=﹣,
综上所述,k的值为3或或﹣或.
【解析】【分析】(1)计算自变量为0时的函数值即可得到C点坐标;
(2)先通过解方程k(x+1)(x﹣)=0得点A、B坐标,讨论:若k>0,当CA=CB,则OA=OB;当AB=AC;当BA=BC时;若k<0时,AB=AC,利用两点间的距离公式分别得到关于k的方程,然后解方程求出对应的k的值.
20.【答案】(1)解:抛物线对称轴为直线x=- =-1,
解得m=-1
函数解析式为y=x2+2x-3,
x … -3 -2 -1 0 1 …
y … 0 -3 -4 -3 0 …
(2)解:∵直线y2=kx+b过点B且与抛物线交于点P(-2,-3),
∴x<-2或x>1时,y2≤y1.
【解析】【分析】(1)由抛物线的对称轴x=1,可以求得m的值,取x与y的值分别填入表中,然后再描点,连线,画出函数的图象;
(2)由图可知,直线y2过点B(1,0)与P(-2,-3),利用待定系数法可以求得k与b的值,画出图像,即可写出y2≤y1时,x的取值。
21.【答案】(1)解:(x-5)(x+1)=0
x1=5,x2=1
(2)解:由题意可知此抛顶点坐标为(a,-1)
设其解析式为=a(x-3)2-1
将点(4,-3)代入得:-3=a-1
解得:a=-2
∴此抛物线解析式为y=-2(x-3)2-1
【解析】【分析】(1)根据解方程的步骤进行计算即可;
(2)根据题意,设出抛物线的解析式,根据待定系数法,得到答案即可。
22.【答案】(1)解:∵,,C是中点,
∴,,
;
,,D是中点
,,
;
(2)解:F是在x轴上,理由如下:
,点A是B关于y轴的对称点,
,
是中点,D是中点,
,则;
轴交抛物线于点,
,
把代入得,,,
,,
轴,且,
是在x轴上;
(3)解:①,,C是中点,
;
是中点,
;
轴交抛物线于点E,
,
把代入得,,
轴交抛物线于点E.延长至F,使得,
,,
,即,
,,
,
点在上,,
,
轴,,
即,,,
综上是一个定值;
②
【解析】【解答】解:(3)②∵是y轴上一点,H是抛物线上任意一点,,
∴当点G、H、F共线时,最小,最小值为的长度,
∵,
∴
,
∵,
∴当时,最小,最小值为,
此时,最小为,
故的最小值为.
【分析】(1)根据中点坐标公式进行解答;
(2)关于y轴对称的点:横坐标互为相反数,纵坐标相同,据此可得点A的坐标,由C是AB的中点,D是BC的中点可得点C、D的坐标,由DE∥y轴可得xE=xD=1,将xE=1代入抛物线解析式中求出yE,得到点E的坐标,然后求出DE、EF的值,据此解答;
(3)①根据中点坐标公式可得点C、D的坐标,由DE∥y轴可得xE=xD,将xE代入抛物线解析式中求出yE,表示出点E的坐标,然后表示出yF,根据点A(m,n)在抛物线上可得n=m2,据此解答;
②由题意可得:当点G、H、F共线时,GH+HF最小,最小值为GF的长度,根据勾股定理表示出GF2,然后根据二次函数的性质进行解答.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
