23.2.3 关于原点对称的点的坐标一课一练(含解析)
文档属性
| 名称 | 23.2.3 关于原点对称的点的坐标一课一练(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 475.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-25 16:29:14 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
23.2.3 关于原点对称的点的坐标一课一练
一、填空题
1.如图,将等边放在平面直角坐标系中,点A的坐标为,点B在第一象限,将等边绕点O顺时针旋转得到,则点的坐标是 .
二、单选题
2.若点关于原点对称的点在第一象限,则a的整数解有( )
A.1个 B.2个 C.3个 D.4个
3.如图所示,边长为2的正三角形ABO的边OB在x轴上,将△ABO绕原点O逆时针旋转30°得到三角形OA1B1,则点A1的坐标为( )
A.( ,1) B.( ,-1) C.(1,- ) D.(2,-1)
4.在平面直角坐标系中,点 关于原点对称的点的坐标是( )
A. B. C. D.
5.已知点A(a,2013)与点A′(﹣2014,b)是关于原点O的对称点,则a+b的值为( )
A.1 B.5 C.6 D.4
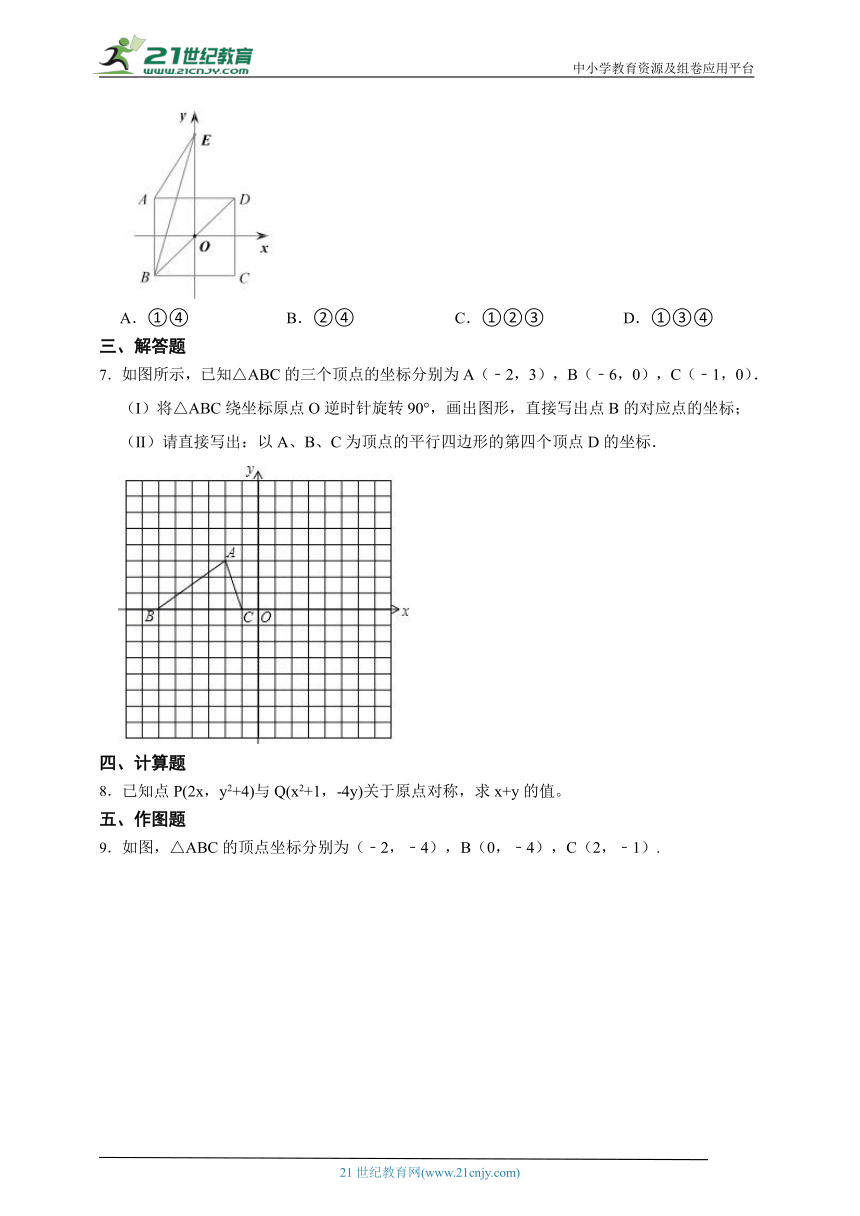
6.如图,正方形ABCD对角线的交点刚好在坐标原点,其中点D坐标为(1,1),若将对角线BD绕点B逆时针旋转30°后所在的直线交y轴于点E,连接AE.下列4个结论:
①点O到直线BE的距离为;②OE的长为;③AB=AE;④直线AE的解析
式为y=x++1.其中正确的是( )
A.①④ B.②④ C.①②③ D.①③④
三、解答题
7.如图所示,已知△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0).
(Ⅰ)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点的坐标;
(Ⅱ)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
四、计算题
8.已知点P(2x,y2+4)与Q(x2+1,-4y)关于原点对称,求x+y的值。
五、作图题
9.如图,△ABC的顶点坐标分别为(﹣2,﹣4),B(0,﹣4),C(2,﹣1).
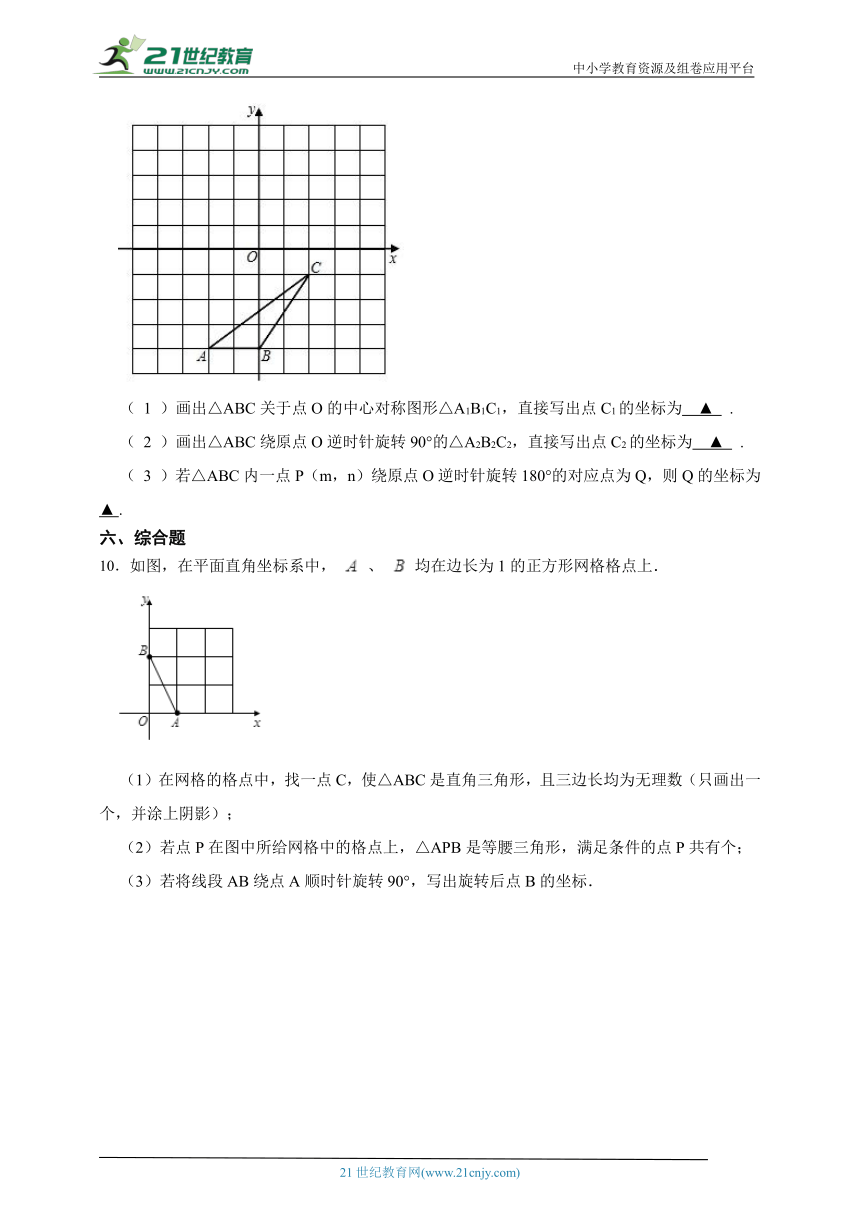
( 1 )画出△ABC关于点O的中心对称图形△A1B1C1,直接写出点C1的坐标为 ▲ .
( 2 )画出△ABC绕原点O逆时针旋转90°的△A2B2C2,直接写出点C2的坐标为 ▲ .
( 3 )若△ABC内一点P(m,n)绕原点O逆时针旋转180°的对应点为Q,则Q的坐标为 ▲ .
六、综合题
10.如图,在平面直角坐标系中, 、 均在边长为1的正方形网格格点上.
(1)在网格的格点中,找一点C,使△ABC是直角三角形,且三边长均为无理数(只画出一个,并涂上阴影);
(2)若点P在图中所给网格中的格点上,△APB是等腰三角形,满足条件的点P共有个;
(3)若将线段AB绕点A顺时针旋转90°,写出旋转后点B的坐标.
答案解析部分
1.【答案】
【解析】【解答】解:作B′H⊥x轴于H,如图
∵△OA′B′为等边三角形,
∴OH=A′H=2,∠B′OA′=60°,
∴B′H=
OH=
,
∴B′点坐标为(2,
),
故答案为:(2,
).
【分析】作B′H⊥x轴于H,求出OH=A′H=2,B′H=
OH=
,可得B′点坐标为(2,
)。
2.【答案】B
【解析】【解答】解:根据题意得点A在第三象限,
,
解得
<a<3,
则a的整数解是1,2.
故答案为:B.
【分析】根据关于原点对称的点坐标的特征及点坐标与象限的关系可得
,再求出a的取值范围即可。
3.【答案】B
【解析】【解答】如图,设A1B1与x轴相交于C,
∵△ABO是等边三角形,旋转角为30°,
∴∠A1OC=60°-30°=30°,
∴A1B1⊥x轴,
∵等边△ABO的边长为2,
∴OC= ×2= ,
A1C= ×2=1,
又∵A1在第四象限,
∴点A1的坐标为( ,-1).
故答案为:B.
【分析】由点A1在坐标系上的位置,排除A;再根据等边三角形的性质求出OC、A1C的长度,再又根据A1在第四象限可得答案。
4.【答案】D
【解析】【解答】解:点 关于原点对称的点的坐标是
故答案为:D.
【分析】关于原点对称的点的坐标特征:横纵坐标分别互为相反数,据此解答即可.
5.【答案】A
【解析】【解答】解:∵点A(a,2013)与点A′(﹣2014,b)是关于原点O的对称点,
∴a=2014,b=﹣2013,
则a+b的值为:2014﹣2013=1.
故选:A.
【分析】根据关于原点对称的点,横坐标与纵坐标都互为相反数解答.
6.【答案】D
【解析】【解答】解:如图,过点O作OH⊥BE于点H,BC交y轴于点F,AD与y轴交于点G,
∴∠OHB=90°,
∵正方形ABCD,D(1,1),
∴GO=1,B(-1,-1),
∴BF=OF=1,BO=,BD=2,
∵∠OBH=30°,
∴OH=BO=,BH=OH=,
∴点O到直线BE的距离为,
∴①说法符合题意;
在Rt△OHE中和Rt△BFE中,
∵∠OEH=∠FEB,
∴△OHE∽△BFE,
∴OH:BF=:1=OE:BE,
设OE=x(x>1),则BE=x,
在Rt△EFB中,BE2=BF2+EF2,
∴2x2=1+(x+1)2,整理得:(x-1)2=3,
解得:x=+1或x=-1(不符合,舍去),
∴OE=+1,
∴②说法不符合题意;
在Rt△AEG中,AG=1,EG=OE-OG= ,
∴AE==2,
又∵AB=2,
∴AB=AE,
∴③说法符合题意;
设直线AE的关系式为y=kx+b,
∵A(-1,1),E(0,+1),
∴
解得 :
∴直线AE的关系式为y=x++1,
∴④说法符合题意,
∴正确的结论有:①③④.
故答案为:D.
【分析】过点O作OH⊥BE于点H,设BC交y轴于点F,AD与y轴交于点G,由正方形性质可得GO=1,B(-1,-1),从而得BF=OF=1,BO=,BD=2,由含30°角直角三角形性质得OH=BO=,BH=OH=,即点O到直线BE的距离为;易证出△OHE∽△BFE,由相似三角形对应比成比例得:1=OE:BE,设OE=x(x>1),则BE=x,由勾股定理得2x2=1+(x+1)2,整理得:(x-1)2=3,解得:x=+1或x=-1(不符合,舍去),即得OE=+1,;在Rt△AEG中,AG=1,EG=OE-OG= ,由勾股定理得AE=2,得AB=AE;设直线AE关系式为y=kx+b,利用待定系数法求得,即得直线AE的关系式为y=x++1. 据此逐项分析,即可得出符合题意的选项.
7.【答案】(Ⅰ)所作图形如图所示:
,
(Ⅱ)点B'的坐标为:(0,-6);
当以AB为对角线时,点D坐标为(-7,3);
当以AC为对角线时,点D坐标为(3,3);
当以BC为对角线时,点D坐标为(-5,-3).
【解析】【分析】(Ⅰ)分别作出点A、B、C绕坐标原点O逆时针旋转90°后的点,然后顺次连接,并写出点B的对应点的坐标;(Ⅱ)分别以AB、BC、AC为对角线,写出第四个顶点D的坐标.
8.【答案】解:依题意:
且
【解析】【分析】利用关于原点对称的点的坐标特征列出方程,求解即可。
9.【答案】解:(1)如图,△A1B1C1即为所求,点C1的坐标为(﹣2,1).
故答案为:(﹣2,1).
(2)如图,△A2B2C2即为所求,点C2的坐标为(1,2),
故答案为:(1,2).
(3)(﹣m,﹣n)
【解析】【解答】解:(3)若△ABC内一点P(m,n)绕原点O逆时针旋转180°的对应点为Q,则Q的坐标为(﹣m,﹣n).
故答案为:(﹣m,﹣n).
【分析】(1)利用关于原点对称点的坐标特点:横纵坐标都互为相反数,可得到点A,B,C关于原点对称的点A1,B1,C1,画出 △A1B1C1,写出点C1的坐标.
(2)利用旋转的性质将△ABC绕原点O逆时针旋转90°,画出旋转后的△A2B2C2,写出点C2的坐标.
(3)将△ABC内一点P(m,n)绕原点O逆时针旋转180°的对应点为Q,可知点P和点Q关于原点对称,可得到点Q的坐标.
10.【答案】(1)解:直角△ABC如图1所示
(2)解:如图,点P共有4个;
(3)解:点B的对应点的坐标为(3,1)
【解析】【分析】(1)根据网格结构及勾股定理作出以点B为直角顶点作边即可解决;
(2)根据等腰三角形的性质,分别以点A,B为顶点作图即可;
(3)根据网格结构找出点B的对应点的位置,然后写出坐标即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
23.2.3 关于原点对称的点的坐标一课一练
一、填空题
1.如图,将等边放在平面直角坐标系中,点A的坐标为,点B在第一象限,将等边绕点O顺时针旋转得到,则点的坐标是 .
二、单选题
2.若点关于原点对称的点在第一象限,则a的整数解有( )
A.1个 B.2个 C.3个 D.4个
3.如图所示,边长为2的正三角形ABO的边OB在x轴上,将△ABO绕原点O逆时针旋转30°得到三角形OA1B1,则点A1的坐标为( )
A.( ,1) B.( ,-1) C.(1,- ) D.(2,-1)
4.在平面直角坐标系中,点 关于原点对称的点的坐标是( )
A. B. C. D.
5.已知点A(a,2013)与点A′(﹣2014,b)是关于原点O的对称点,则a+b的值为( )
A.1 B.5 C.6 D.4
6.如图,正方形ABCD对角线的交点刚好在坐标原点,其中点D坐标为(1,1),若将对角线BD绕点B逆时针旋转30°后所在的直线交y轴于点E,连接AE.下列4个结论:
①点O到直线BE的距离为;②OE的长为;③AB=AE;④直线AE的解析
式为y=x++1.其中正确的是( )
A.①④ B.②④ C.①②③ D.①③④
三、解答题
7.如图所示,已知△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0).
(Ⅰ)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点的坐标;
(Ⅱ)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
四、计算题
8.已知点P(2x,y2+4)与Q(x2+1,-4y)关于原点对称,求x+y的值。
五、作图题
9.如图,△ABC的顶点坐标分别为(﹣2,﹣4),B(0,﹣4),C(2,﹣1).
( 1 )画出△ABC关于点O的中心对称图形△A1B1C1,直接写出点C1的坐标为 ▲ .
( 2 )画出△ABC绕原点O逆时针旋转90°的△A2B2C2,直接写出点C2的坐标为 ▲ .
( 3 )若△ABC内一点P(m,n)绕原点O逆时针旋转180°的对应点为Q,则Q的坐标为 ▲ .
六、综合题
10.如图,在平面直角坐标系中, 、 均在边长为1的正方形网格格点上.
(1)在网格的格点中,找一点C,使△ABC是直角三角形,且三边长均为无理数(只画出一个,并涂上阴影);
(2)若点P在图中所给网格中的格点上,△APB是等腰三角形,满足条件的点P共有个;
(3)若将线段AB绕点A顺时针旋转90°,写出旋转后点B的坐标.
答案解析部分
1.【答案】
【解析】【解答】解:作B′H⊥x轴于H,如图
∵△OA′B′为等边三角形,
∴OH=A′H=2,∠B′OA′=60°,
∴B′H=
OH=
,
∴B′点坐标为(2,
),
故答案为:(2,
).
【分析】作B′H⊥x轴于H,求出OH=A′H=2,B′H=
OH=
,可得B′点坐标为(2,
)。
2.【答案】B
【解析】【解答】解:根据题意得点A在第三象限,
,
解得
<a<3,
则a的整数解是1,2.
故答案为:B.
【分析】根据关于原点对称的点坐标的特征及点坐标与象限的关系可得
,再求出a的取值范围即可。
3.【答案】B
【解析】【解答】如图,设A1B1与x轴相交于C,
∵△ABO是等边三角形,旋转角为30°,
∴∠A1OC=60°-30°=30°,
∴A1B1⊥x轴,
∵等边△ABO的边长为2,
∴OC= ×2= ,
A1C= ×2=1,
又∵A1在第四象限,
∴点A1的坐标为( ,-1).
故答案为:B.
【分析】由点A1在坐标系上的位置,排除A;再根据等边三角形的性质求出OC、A1C的长度,再又根据A1在第四象限可得答案。
4.【答案】D
【解析】【解答】解:点 关于原点对称的点的坐标是
故答案为:D.
【分析】关于原点对称的点的坐标特征:横纵坐标分别互为相反数,据此解答即可.
5.【答案】A
【解析】【解答】解:∵点A(a,2013)与点A′(﹣2014,b)是关于原点O的对称点,
∴a=2014,b=﹣2013,
则a+b的值为:2014﹣2013=1.
故选:A.
【分析】根据关于原点对称的点,横坐标与纵坐标都互为相反数解答.
6.【答案】D
【解析】【解答】解:如图,过点O作OH⊥BE于点H,BC交y轴于点F,AD与y轴交于点G,
∴∠OHB=90°,
∵正方形ABCD,D(1,1),
∴GO=1,B(-1,-1),
∴BF=OF=1,BO=,BD=2,
∵∠OBH=30°,
∴OH=BO=,BH=OH=,
∴点O到直线BE的距离为,
∴①说法符合题意;
在Rt△OHE中和Rt△BFE中,
∵∠OEH=∠FEB,
∴△OHE∽△BFE,
∴OH:BF=:1=OE:BE,
设OE=x(x>1),则BE=x,
在Rt△EFB中,BE2=BF2+EF2,
∴2x2=1+(x+1)2,整理得:(x-1)2=3,
解得:x=+1或x=-1(不符合,舍去),
∴OE=+1,
∴②说法不符合题意;
在Rt△AEG中,AG=1,EG=OE-OG= ,
∴AE==2,
又∵AB=2,
∴AB=AE,
∴③说法符合题意;
设直线AE的关系式为y=kx+b,
∵A(-1,1),E(0,+1),
∴
解得 :
∴直线AE的关系式为y=x++1,
∴④说法符合题意,
∴正确的结论有:①③④.
故答案为:D.
【分析】过点O作OH⊥BE于点H,设BC交y轴于点F,AD与y轴交于点G,由正方形性质可得GO=1,B(-1,-1),从而得BF=OF=1,BO=,BD=2,由含30°角直角三角形性质得OH=BO=,BH=OH=,即点O到直线BE的距离为;易证出△OHE∽△BFE,由相似三角形对应比成比例得:1=OE:BE,设OE=x(x>1),则BE=x,由勾股定理得2x2=1+(x+1)2,整理得:(x-1)2=3,解得:x=+1或x=-1(不符合,舍去),即得OE=+1,;在Rt△AEG中,AG=1,EG=OE-OG= ,由勾股定理得AE=2,得AB=AE;设直线AE关系式为y=kx+b,利用待定系数法求得,即得直线AE的关系式为y=x++1. 据此逐项分析,即可得出符合题意的选项.
7.【答案】(Ⅰ)所作图形如图所示:
,
(Ⅱ)点B'的坐标为:(0,-6);
当以AB为对角线时,点D坐标为(-7,3);
当以AC为对角线时,点D坐标为(3,3);
当以BC为对角线时,点D坐标为(-5,-3).
【解析】【分析】(Ⅰ)分别作出点A、B、C绕坐标原点O逆时针旋转90°后的点,然后顺次连接,并写出点B的对应点的坐标;(Ⅱ)分别以AB、BC、AC为对角线,写出第四个顶点D的坐标.
8.【答案】解:依题意:
且
【解析】【分析】利用关于原点对称的点的坐标特征列出方程,求解即可。
9.【答案】解:(1)如图,△A1B1C1即为所求,点C1的坐标为(﹣2,1).
故答案为:(﹣2,1).
(2)如图,△A2B2C2即为所求,点C2的坐标为(1,2),
故答案为:(1,2).
(3)(﹣m,﹣n)
【解析】【解答】解:(3)若△ABC内一点P(m,n)绕原点O逆时针旋转180°的对应点为Q,则Q的坐标为(﹣m,﹣n).
故答案为:(﹣m,﹣n).
【分析】(1)利用关于原点对称点的坐标特点:横纵坐标都互为相反数,可得到点A,B,C关于原点对称的点A1,B1,C1,画出 △A1B1C1,写出点C1的坐标.
(2)利用旋转的性质将△ABC绕原点O逆时针旋转90°,画出旋转后的△A2B2C2,写出点C2的坐标.
(3)将△ABC内一点P(m,n)绕原点O逆时针旋转180°的对应点为Q,可知点P和点Q关于原点对称,可得到点Q的坐标.
10.【答案】(1)解:直角△ABC如图1所示
(2)解:如图,点P共有4个;
(3)解:点B的对应点的坐标为(3,1)
【解析】【分析】(1)根据网格结构及勾股定理作出以点B为直角顶点作边即可解决;
(2)根据等腰三角形的性质,分别以点A,B为顶点作图即可;
(3)根据网格结构找出点B的对应点的位置,然后写出坐标即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
