23.2 中心对称基础知识测试题(含解析)
文档属性
| 名称 | 23.2 中心对称基础知识测试题(含解析) |

|
|
| 格式 | doc | ||
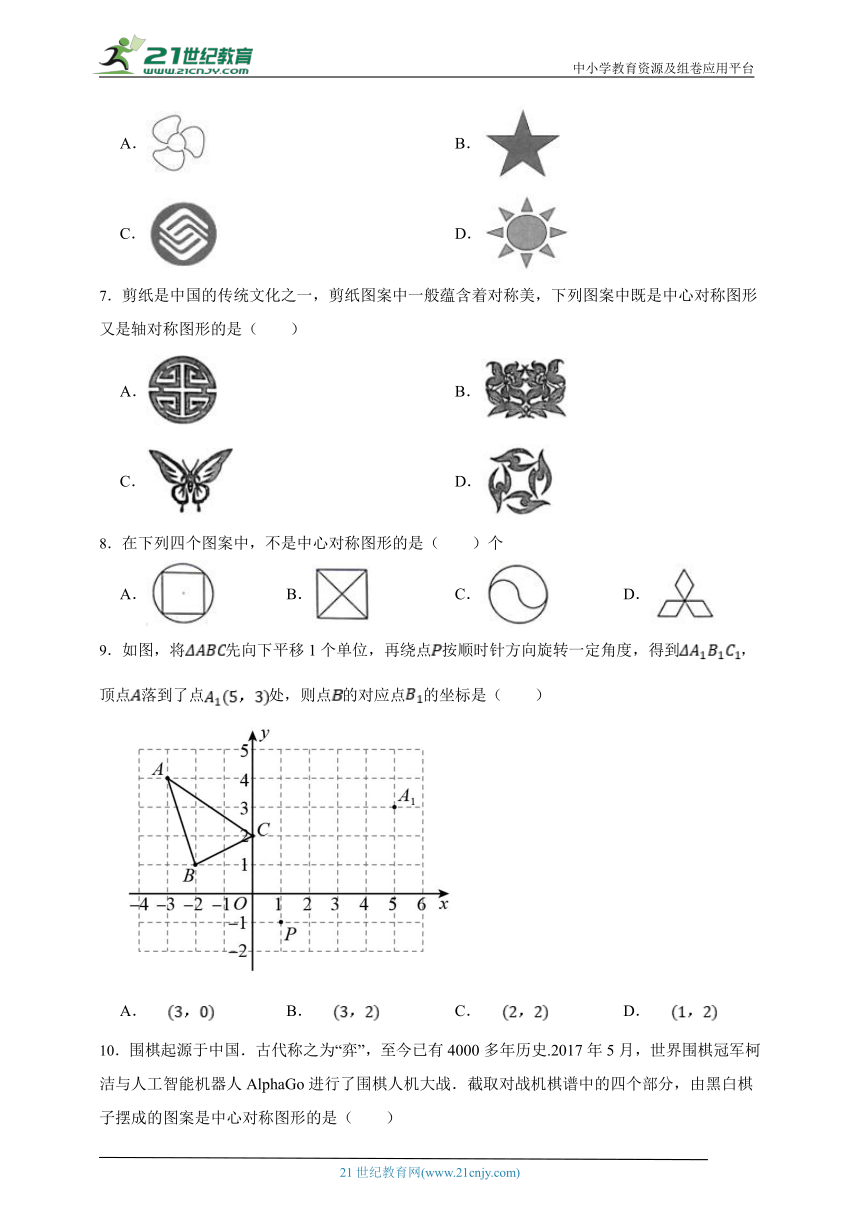
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-25 16:37:14 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
23.2 中心对称基础知识测试题
一、单选题
1.随着国民经济快速发展,我国涌现出一批规模大、效益高的企业,如大疆、国家核电、华为、凤凰光学等,以上四个企业的标志是中心对称图形的是( )
A. B.
C. D.
2.下列汽车标志中既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
3.下面的图形既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
4.在平面直角坐标系 中,点 的坐标是 ,连接 ,将线段 绕原点 旋转 ,得到对应线段 ,则点 的坐标是( )
A. B. C. D.
5.下列图形中,是中心对称图形的是( )
A. B.
C. D.
6.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
7.剪纸是中国的传统文化之一,剪纸图案中一般蕴含着对称美,下列图案中既是中心对称图形又是轴对称图形的是( )
A. B.
C. D.
8.在下列四个图案中,不是中心对称图形的是( )个
A. B. C. D.
9.如图,将先向下平移1个单位,再绕点按顺时针方向旋转一定角度,得到,顶点落到了点处,则点的对应点的坐标是( )
A. B. C. D.
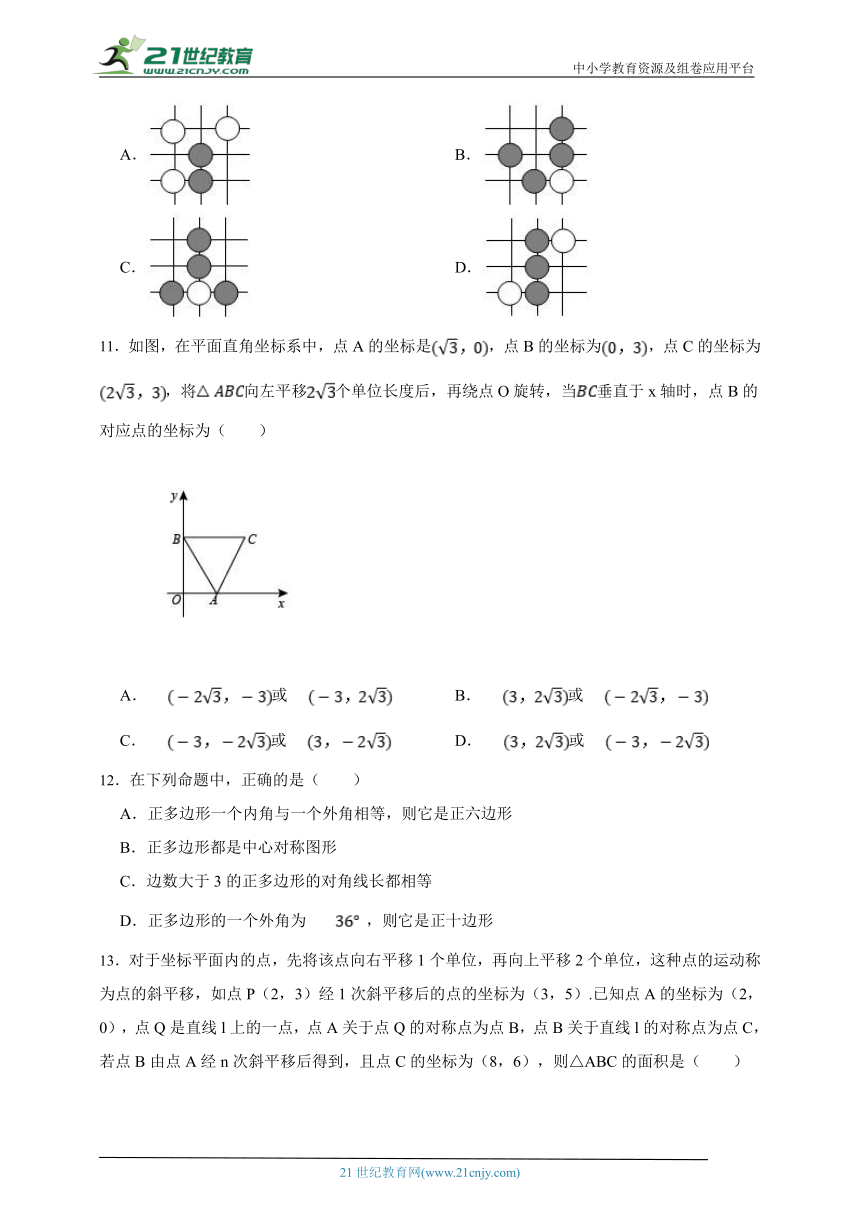
10.围棋起源于中国.古代称之为“弈”,至今已有4000多年历史.2017年5月,世界围棋冠军柯洁与人工智能机器人AlphaGo进行了围棋人机大战.截取对战机棋谱中的四个部分,由黑白棋子摆成的图案是中心对称图形的是( )
A. B.
C. D.
11.如图,在平面直角坐标系中,点A的坐标是,点B的坐标为,点C的坐标为,将向左平移个单位长度后,再绕点O旋转,当垂直于x轴时,点B的对应点的坐标为( )
A.或 B.或
C.或 D.或
12.在下列命题中,正确的是( )
A.正多边形一个内角与一个外角相等,则它是正六边形
B.正多边形都是中心对称图形
C.边数大于3的正多边形的对角线长都相等
D.正多边形的一个外角为 ,则它是正十边形
13.对于坐标平面内的点,先将该点向右平移1个单位,再向上平移2个单位,这种点的运动称为点的斜平移,如点P(2,3)经1次斜平移后的点的坐标为(3,5).已知点A的坐标为(2,0),点Q是直线l上的一点,点A关于点Q的对称点为点B,点B关于直线l的对称点为点C,若点B由点A经n次斜平移后得到,且点C的坐标为(8,6),则△ABC的面积是( )
A.12 B.14 C.16 D.18
二、填空题
14.如图,将n个边长都为1cm的正方形按如图所示摆放,点A1, A2,…,An分别是正方形的中心,则n个正方形重叠形成的重叠部分的面积和为
三、计算题
15.已知点P(2x,y2+4)与Q(x2+1,-4y)关于原点对称,求x+y的值。
四、解答题
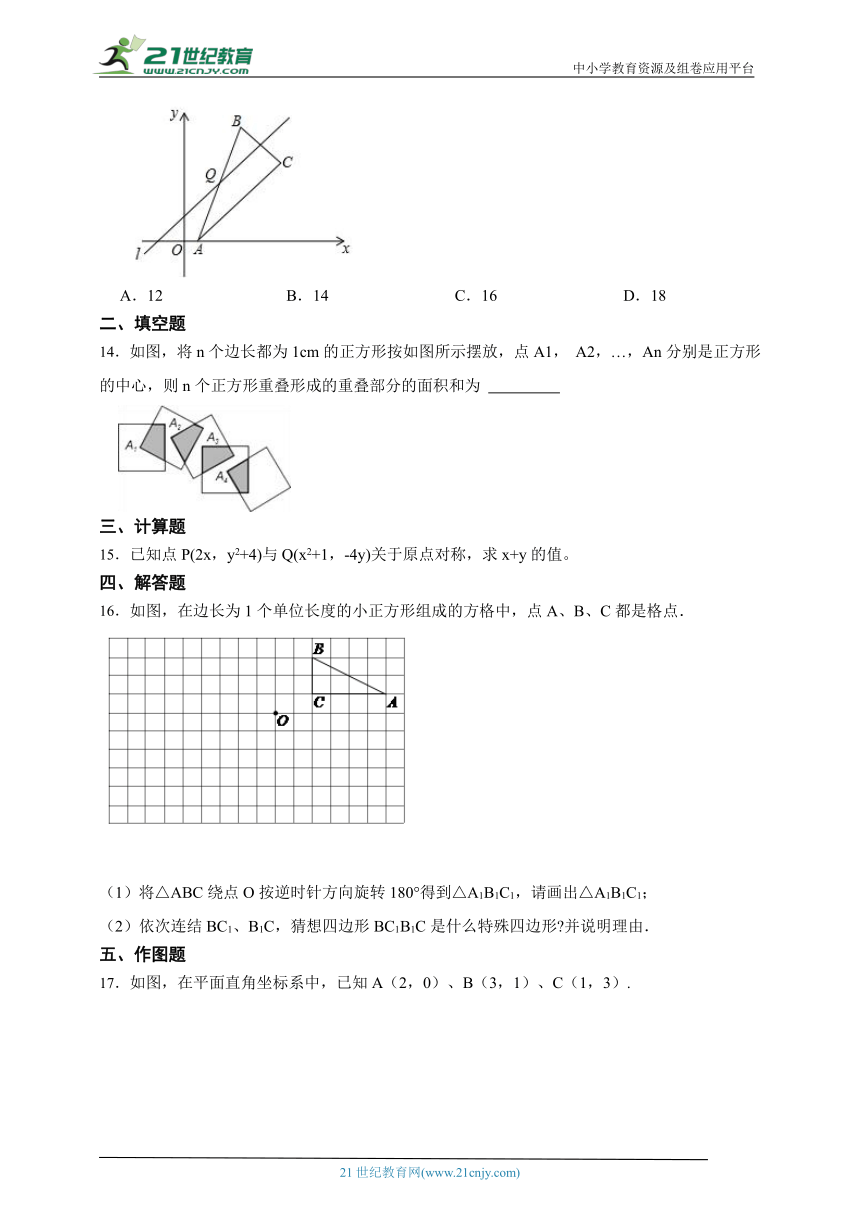
16.如图,在边长为1个单位长度的小正方形组成的方格中,点A、B、C都是格点.
(1)将△ABC绕点O按逆时针方向旋转180°得到△A1B1C1,请画出△A1B1C1;
(2)依次连结BC1、B1C,猜想四边形BC1B1C是什么特殊四边形 并说明理由.
五、作图题
17.如图,在平面直角坐标系中,已知A(2,0)、B(3,1)、C(1,3).
(1)①将△ABC沿x轴负方向移动2个单位长度至△A1B1C1,画图并写出点C1的坐标;
②以点A1为旋转中心,将△A1B1C1逆时针方向旋转90°得到△A2B2C2,画图并写出点C2的坐标;
(2)以B、C1、C2为顶点的三角形是 三角形,其外接圆的半径R= .
六、综合题
18.如图,△ABC在平面直角坐标系内,顶点的坐标分别为A(﹣4,4),B(﹣2,5),C(﹣2,1).
(1)①平移△ABC,使点C移到点C1(﹣2,﹣4),画出平移后的△A1B1C1,并写出点A1,B1的坐标;
②将△ABC绕点(0,3)旋转180°,得到△A2B2C2,画出旋转后的△A2B2C2;
(2)求(1)②中的点C旋转到点C2时,点C经过的路径长(结果保留π).
七、实践探究题
19.阅读材料,并回答下列问题:
如图1,以AB为轴,把△ABC翻折180°,可以变换到△ABD的位置;如图2,把△ABC沿射线AC平移,可以变换到△DEF的位置.像这样,其中的一个三角形是另一个三角形经翻折、平移等方法变换成的,这种只改变位置,不改变形状大小的图形变换,叫三角形的全等变换.
(1)请你写出一种全等变换的方法(除翻折、平移外). ;
(2)如图2,△ABC沿射线AC平移到△DEF,若平移的距离为2,且AC=3,则DC= ;
(3)如图3,D、E分别是△ABC的边AB、AC上的点,把△ADE沿DE翻折,当点A落在四边形BCED内部变为F时,则∠F和∠BDF+∠CEF之间的数量关系始终保持不变,请你直接写出它们之间的关系式: .
答案解析部分
1.【答案】B
【解析】【分析】在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,据此依次判断即可.
2.【答案】C
【解析】【解答】解:A是轴对称图形,B既不是轴对称图形也不是中心对称图形,C既是轴对称图形又是中心对称图形,D是轴对称图形.故答案为:C.
【分析】把一个平面图形,沿着某一条直线折叠,直线两旁的部分能完全重合的平面图形就是轴对称图形;把一个平面图像绕着某一点旋转180°后能与自身重合的图形就是中心对称图形,根据定义即可一一判断得出答案。
3.【答案】D
【解析】【解答】解:A.不是轴对称图形,是中心对称图形,故此选项不合题意;
B.是轴对称图形,不是中心对称图形,故此选项不合题意;
C.不是轴对称图形,也不是中心对称图形,故此选项不合题意;
D.是轴对称图形,也是中心对称图形,故此选项符合题意;
故答案为:D.
【分析】中心对称图形是图形绕某一点旋转180°后与原来的图形完全重合,轴对称图形是将一个图形沿某直线折叠后直线两旁的部分互相重合,再对各选项逐一判断.
4.【答案】A
【解析】【解答】解:如图,观察图象可知,B(2,-1).
故答案为:A.
【分析】 将线段 绕原点 旋转 得到对应线段 ,则OA与OB关于原点对称,于是根据关于原点对称的坐标特点即可得出B点坐标.
5.【答案】D
【解析】【解答】解:A、不是中心对称图形,故不符合题意;
B、不是中心对称图形,故不符合题意;
C、不是中心对称图形,故不符合题意;
D、是中心对称图形,故符合题意;
故答案为:D.
【分析】把一个平面图形,沿着某一点旋转180°后,能与自身重合的图形就是中心对称图形,根据定义即可一一判断得出答案.
6.【答案】D
【解析】【解答】解:A、不是轴对称图形,也不是中心对称图形,故本选项错误;
B、是轴对称图形,不是中心对称图形,故本选项错误;
C、不是轴对称图形,是中心对称图形,故本选项错误;
D、是轴对称图形,也是中心对称图形,故本选项正确.
故答案为:D.
【分析】中心对称图形是图形绕某一点旋转180°后与原来的图形完全重合;轴对称图形是将一个图形沿某直线折叠后直线两旁的部分互相重合,据此再对各选项逐一判断.
7.【答案】A
【解析】【解答】解:A.既是轴对称图形,又是中心对称图形,故本选项符合题意;
B.是轴对称图形,不是中心对称图形,故本选项不符合题意;
C.是轴对称图形,不是中心对称图形,故本选项不符合题意;
D.不是轴对称图形,是中心对称图形,故本选项不符合题意.
故答案为:A.
【分析】根据轴对称图形和中心对称图形的定义逐项判断即可。
8.【答案】D
【解析】【解答】解:A、.是中心对称图形,故不符合题意;
B、是中心对称图形,故不符合题意;
C、 是中心对称图形,故不符合题意;
D、不是中心对称图形,符合题意.
故答案为:D.
【分析】中心对称图形,就是一个图形绕一个中心旋转180°后,能与原来的图形完全重合的图形,根据定义分别判断即可.
9.【答案】C
【解析】【解答】解:如图,点的对应点的坐标是,
故答案为:C.
【分析】根据点坐标平移及旋转的特征求解即可。
10.【答案】D
【解析】【解答】解:A中图形不是中心对称图形,不符合题意;
B中图形不是中心对称图形,不符合题意;
C中图形不是中心对称图形,不符合题意;
D中图形是中心对称图形,符合题意;
故答案为:D.
【分析】根据中心对称图形的定义逐项判断即可。
11.【答案】D
【解析】【解答】解:如图,将向左平移个单位长度后,得到,
将绕点O逆时针旋转90°后,得到,此时B1C1⊥x轴,
∵C′(0,3),∴C1(-3,0),∵B1C1=,∴B1(-3,-);
将绕点O顺时针旋转90°后,得到,此时B2C2⊥x轴,
∵C′(0,3),∴C2(3,0),∵B2C2=,∴B2(3,);
∴点B的对应点的坐标为(-3,-)或(3,);
故答案为:D.
【分析】根据点坐标平移和点坐标旋转的性质求解即可。
12.【答案】D
【解析】【解答】A.正多边形一个内角与一个外角相等,则它是正六边形,故本选项错误;
B.正多边形不一定是中心对称图形,故本选项错误;
C.边数大于3的正多边形的对角线长不一定相等,故本选项错误;
D.正多边形的一个外角为 ,则它是正十边形,故本选项正确.
故答案为:D.
【分析】分析是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案.
13.【答案】A
【解析】【解答】解:连接CQ,如图:
由中心对称可知,AQ=BQ,
由轴对称可知:BQ=CQ,
∴AQ=CQ=BQ,
∴∠QAC=∠ACQ,∠QBC=∠QCB,
∵∠QAC+∠ACQ+∠QBC+∠QCB=180°,
∴∠ACQ+∠QCB=90°,
∴∠ACB=90°,
∴△ABC是直角三角形,
延长BC交x轴于点E,过C点作CF⊥AE于点F,如图,
∵A(2,0),C(8,6),
∴AF=CF=6,
∴△ACF是等腰直角三角形,
∵,
∴∠AEC=45°,
∴E点坐标为(14,0),
设直线BE的解析式为y=kx+b,
∵C,E点在直线上,
可得:,
解得:,
∴y=﹣x+14,
∵点B由点A经n次斜平移得到,
∴点B(n+2,2n),由2n=﹣n﹣2+14,
解得:n=4,
∴B(6,8),
∴△ABC的面积=S△ABE﹣S△ACE=×12×8﹣×12×6=12,
故答案为:A.
【分析】连接CQ,根据中心对称性质得AQ=BQ,由轴对称性质得BQ=CQ,利用斜边中线性质定理逆定理可判定△ABC为直角三角形,即∠ACB=90°;延长BC交x轴于点E,过C点作CF⊥AE于点F,利用待定系数法求得直线BE解析式,根据B由A点经n次斜平移得到进而求出B点坐标,最后利用S△ABC=S△ABE﹣S△ACE求出面积。
14.【答案】
【解析】【解答】解:由题意可得阴影部分面积等于正方形面积的 ,即是 ,
5个这样的正方形重叠部分(阴影部分)的面积和为 ×4,
n个这样的正方形重叠部分(阴影部分)的面积和为 ×(n-1)= cm2.
【分析】根据题意可得出,阴影部分面积等于正方形面积的 ,已知两个正方形可得出一个阴影部分,则n个这样的正方形重叠部分为n-1阴影部分的和。
15.【答案】解:依题意:
且
【解析】【分析】利用关于原点对称的点的坐标特征列出方程,求解即可。
16.【答案】解:(1)如图:△A1B1C1为所求作的三角形;
(2)四边形BC1B1C是平行四边形
连结BB1,CC1,
∵点B与B1,点C与C1分别关于点O成中心对称,
∴OB= OB1,OC= OC1,
∴四边形BC1B1C是平行四边形.
【解析】【分析】(1)将点A、B、C分别绕点O按逆时针方向旋转180°,得出对应点,即可得出△A1B1C1;
(2)连结BC1、B1C,BB1,CC1,由(1)可得点B与B1,点C与C1分别关于点O成中心对称,继而得出OB=OB1,OC=OC1,可证明四边形BC1B1C是平行四边形.
17.【答案】(1)解:如图所示,△A1B1C1、△A2B2C2即为所求,其中C1的坐标为(﹣1,3),其中点C2的坐标为(﹣3,﹣1);
(2)直角;
【解析】【解答】解:(3)∵C1C22=BC12=22+42=20,BC22=22+62=40,
∴C1C22+BC12=BC22,
∴△BC1C2是直角三角形,
则外接圆的半径R= BC2= ×2 = .
故答案为:直角, .
【分析】(1)①将三个顶点分别向左平移2个单位得到其对应点,再顺次连接即可得;②将三个顶点分别以点A1为旋转中心,逆时针方向旋转90°得到对应点,再顺次连接即可得;(2)利用勾股定理及其逆定理(如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形)求解可得.
18.【答案】(1)解:如图所示,则△A1B1C1、△A2B2C2为所求作的三角形,
∴A1(-4,-1),B1(-2,0)
(2)解:点C经过的路径长:是以(0,3)为圆心,以CC2为直径的半圆,
由勾股定理得:CC2= ,
∴点C经过的路径长:
【解析】【分析】(1)根据点C移到点C1(﹣2,﹣4),可知向下平移了5个单位,分别作出A、B、C的对应点A1、B1、C1即可解决问题。
(2)根据中心对称的性质,作出A、B、C的对应点A2、B2、C2即可。
(3)利用勾股定理求出CC2的长,可得半径为2,根据圆的周长公式计算即可。
19.【答案】(1)旋转
(2)1
(3)∠BDF+∠CEF=2∠F
【解析】【解答】解:(1)旋转;
( 2 )∵AD=2,
∴DC=AC﹣AD=3﹣2=1;
( 3 )∵把△ADE沿DE翻折,得到△FDE,
∴∠ADE=∠FDE,∠AED=∠FED,
在△DEF中,∠F=180°﹣(∠FDE+∠FED);
由平角定义知,∠BDF=180°﹣∠FDA=180°﹣2∠FDE,
∠CEF=180°﹣∠FEA=180°﹣2∠FED,
∴∠BDF+∠CEF=180°﹣2∠FDE+180°﹣2∠FED=2[180°﹣(∠FDE+∠FED)]
∴∠BDF+∠CEF=2∠F.
【分析】(1)旋转变换是指一个图形围绕一个定点旋转一定的角度,得到另一个图形;于是可由平移得到全等变换;
(2)由平移的性质可知,AD=2,所以DC=AC-AD可求解;
(3)由轴对称的性质可得∠ADE=∠EDF,∠AED=∠FED,再结合三角形的内角和定理即可求解。
23.2 中心对称基础知识测试题
一、单选题
1.随着国民经济快速发展,我国涌现出一批规模大、效益高的企业,如大疆、国家核电、华为、凤凰光学等,以上四个企业的标志是中心对称图形的是( )
A. B.
C. D.
2.下列汽车标志中既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
3.下面的图形既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
4.在平面直角坐标系 中,点 的坐标是 ,连接 ,将线段 绕原点 旋转 ,得到对应线段 ,则点 的坐标是( )
A. B. C. D.
5.下列图形中,是中心对称图形的是( )
A. B.
C. D.
6.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
7.剪纸是中国的传统文化之一,剪纸图案中一般蕴含着对称美,下列图案中既是中心对称图形又是轴对称图形的是( )
A. B.
C. D.
8.在下列四个图案中,不是中心对称图形的是( )个
A. B. C. D.
9.如图,将先向下平移1个单位,再绕点按顺时针方向旋转一定角度,得到,顶点落到了点处,则点的对应点的坐标是( )
A. B. C. D.
10.围棋起源于中国.古代称之为“弈”,至今已有4000多年历史.2017年5月,世界围棋冠军柯洁与人工智能机器人AlphaGo进行了围棋人机大战.截取对战机棋谱中的四个部分,由黑白棋子摆成的图案是中心对称图形的是( )
A. B.
C. D.
11.如图,在平面直角坐标系中,点A的坐标是,点B的坐标为,点C的坐标为,将向左平移个单位长度后,再绕点O旋转,当垂直于x轴时,点B的对应点的坐标为( )
A.或 B.或
C.或 D.或
12.在下列命题中,正确的是( )
A.正多边形一个内角与一个外角相等,则它是正六边形
B.正多边形都是中心对称图形
C.边数大于3的正多边形的对角线长都相等
D.正多边形的一个外角为 ,则它是正十边形
13.对于坐标平面内的点,先将该点向右平移1个单位,再向上平移2个单位,这种点的运动称为点的斜平移,如点P(2,3)经1次斜平移后的点的坐标为(3,5).已知点A的坐标为(2,0),点Q是直线l上的一点,点A关于点Q的对称点为点B,点B关于直线l的对称点为点C,若点B由点A经n次斜平移后得到,且点C的坐标为(8,6),则△ABC的面积是( )
A.12 B.14 C.16 D.18
二、填空题
14.如图,将n个边长都为1cm的正方形按如图所示摆放,点A1, A2,…,An分别是正方形的中心,则n个正方形重叠形成的重叠部分的面积和为
三、计算题
15.已知点P(2x,y2+4)与Q(x2+1,-4y)关于原点对称,求x+y的值。
四、解答题
16.如图,在边长为1个单位长度的小正方形组成的方格中,点A、B、C都是格点.
(1)将△ABC绕点O按逆时针方向旋转180°得到△A1B1C1,请画出△A1B1C1;
(2)依次连结BC1、B1C,猜想四边形BC1B1C是什么特殊四边形 并说明理由.
五、作图题
17.如图,在平面直角坐标系中,已知A(2,0)、B(3,1)、C(1,3).
(1)①将△ABC沿x轴负方向移动2个单位长度至△A1B1C1,画图并写出点C1的坐标;
②以点A1为旋转中心,将△A1B1C1逆时针方向旋转90°得到△A2B2C2,画图并写出点C2的坐标;
(2)以B、C1、C2为顶点的三角形是 三角形,其外接圆的半径R= .
六、综合题
18.如图,△ABC在平面直角坐标系内,顶点的坐标分别为A(﹣4,4),B(﹣2,5),C(﹣2,1).
(1)①平移△ABC,使点C移到点C1(﹣2,﹣4),画出平移后的△A1B1C1,并写出点A1,B1的坐标;
②将△ABC绕点(0,3)旋转180°,得到△A2B2C2,画出旋转后的△A2B2C2;
(2)求(1)②中的点C旋转到点C2时,点C经过的路径长(结果保留π).
七、实践探究题
19.阅读材料,并回答下列问题:
如图1,以AB为轴,把△ABC翻折180°,可以变换到△ABD的位置;如图2,把△ABC沿射线AC平移,可以变换到△DEF的位置.像这样,其中的一个三角形是另一个三角形经翻折、平移等方法变换成的,这种只改变位置,不改变形状大小的图形变换,叫三角形的全等变换.
(1)请你写出一种全等变换的方法(除翻折、平移外). ;
(2)如图2,△ABC沿射线AC平移到△DEF,若平移的距离为2,且AC=3,则DC= ;
(3)如图3,D、E分别是△ABC的边AB、AC上的点,把△ADE沿DE翻折,当点A落在四边形BCED内部变为F时,则∠F和∠BDF+∠CEF之间的数量关系始终保持不变,请你直接写出它们之间的关系式: .
答案解析部分
1.【答案】B
【解析】【分析】在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,据此依次判断即可.
2.【答案】C
【解析】【解答】解:A是轴对称图形,B既不是轴对称图形也不是中心对称图形,C既是轴对称图形又是中心对称图形,D是轴对称图形.故答案为:C.
【分析】把一个平面图形,沿着某一条直线折叠,直线两旁的部分能完全重合的平面图形就是轴对称图形;把一个平面图像绕着某一点旋转180°后能与自身重合的图形就是中心对称图形,根据定义即可一一判断得出答案。
3.【答案】D
【解析】【解答】解:A.不是轴对称图形,是中心对称图形,故此选项不合题意;
B.是轴对称图形,不是中心对称图形,故此选项不合题意;
C.不是轴对称图形,也不是中心对称图形,故此选项不合题意;
D.是轴对称图形,也是中心对称图形,故此选项符合题意;
故答案为:D.
【分析】中心对称图形是图形绕某一点旋转180°后与原来的图形完全重合,轴对称图形是将一个图形沿某直线折叠后直线两旁的部分互相重合,再对各选项逐一判断.
4.【答案】A
【解析】【解答】解:如图,观察图象可知,B(2,-1).
故答案为:A.
【分析】 将线段 绕原点 旋转 得到对应线段 ,则OA与OB关于原点对称,于是根据关于原点对称的坐标特点即可得出B点坐标.
5.【答案】D
【解析】【解答】解:A、不是中心对称图形,故不符合题意;
B、不是中心对称图形,故不符合题意;
C、不是中心对称图形,故不符合题意;
D、是中心对称图形,故符合题意;
故答案为:D.
【分析】把一个平面图形,沿着某一点旋转180°后,能与自身重合的图形就是中心对称图形,根据定义即可一一判断得出答案.
6.【答案】D
【解析】【解答】解:A、不是轴对称图形,也不是中心对称图形,故本选项错误;
B、是轴对称图形,不是中心对称图形,故本选项错误;
C、不是轴对称图形,是中心对称图形,故本选项错误;
D、是轴对称图形,也是中心对称图形,故本选项正确.
故答案为:D.
【分析】中心对称图形是图形绕某一点旋转180°后与原来的图形完全重合;轴对称图形是将一个图形沿某直线折叠后直线两旁的部分互相重合,据此再对各选项逐一判断.
7.【答案】A
【解析】【解答】解:A.既是轴对称图形,又是中心对称图形,故本选项符合题意;
B.是轴对称图形,不是中心对称图形,故本选项不符合题意;
C.是轴对称图形,不是中心对称图形,故本选项不符合题意;
D.不是轴对称图形,是中心对称图形,故本选项不符合题意.
故答案为:A.
【分析】根据轴对称图形和中心对称图形的定义逐项判断即可。
8.【答案】D
【解析】【解答】解:A、.是中心对称图形,故不符合题意;
B、是中心对称图形,故不符合题意;
C、 是中心对称图形,故不符合题意;
D、不是中心对称图形,符合题意.
故答案为:D.
【分析】中心对称图形,就是一个图形绕一个中心旋转180°后,能与原来的图形完全重合的图形,根据定义分别判断即可.
9.【答案】C
【解析】【解答】解:如图,点的对应点的坐标是,
故答案为:C.
【分析】根据点坐标平移及旋转的特征求解即可。
10.【答案】D
【解析】【解答】解:A中图形不是中心对称图形,不符合题意;
B中图形不是中心对称图形,不符合题意;
C中图形不是中心对称图形,不符合题意;
D中图形是中心对称图形,符合题意;
故答案为:D.
【分析】根据中心对称图形的定义逐项判断即可。
11.【答案】D
【解析】【解答】解:如图,将向左平移个单位长度后,得到,
将绕点O逆时针旋转90°后,得到,此时B1C1⊥x轴,
∵C′(0,3),∴C1(-3,0),∵B1C1=,∴B1(-3,-);
将绕点O顺时针旋转90°后,得到,此时B2C2⊥x轴,
∵C′(0,3),∴C2(3,0),∵B2C2=,∴B2(3,);
∴点B的对应点的坐标为(-3,-)或(3,);
故答案为:D.
【分析】根据点坐标平移和点坐标旋转的性质求解即可。
12.【答案】D
【解析】【解答】A.正多边形一个内角与一个外角相等,则它是正六边形,故本选项错误;
B.正多边形不一定是中心对称图形,故本选项错误;
C.边数大于3的正多边形的对角线长不一定相等,故本选项错误;
D.正多边形的一个外角为 ,则它是正十边形,故本选项正确.
故答案为:D.
【分析】分析是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案.
13.【答案】A
【解析】【解答】解:连接CQ,如图:
由中心对称可知,AQ=BQ,
由轴对称可知:BQ=CQ,
∴AQ=CQ=BQ,
∴∠QAC=∠ACQ,∠QBC=∠QCB,
∵∠QAC+∠ACQ+∠QBC+∠QCB=180°,
∴∠ACQ+∠QCB=90°,
∴∠ACB=90°,
∴△ABC是直角三角形,
延长BC交x轴于点E,过C点作CF⊥AE于点F,如图,
∵A(2,0),C(8,6),
∴AF=CF=6,
∴△ACF是等腰直角三角形,
∵,
∴∠AEC=45°,
∴E点坐标为(14,0),
设直线BE的解析式为y=kx+b,
∵C,E点在直线上,
可得:,
解得:,
∴y=﹣x+14,
∵点B由点A经n次斜平移得到,
∴点B(n+2,2n),由2n=﹣n﹣2+14,
解得:n=4,
∴B(6,8),
∴△ABC的面积=S△ABE﹣S△ACE=×12×8﹣×12×6=12,
故答案为:A.
【分析】连接CQ,根据中心对称性质得AQ=BQ,由轴对称性质得BQ=CQ,利用斜边中线性质定理逆定理可判定△ABC为直角三角形,即∠ACB=90°;延长BC交x轴于点E,过C点作CF⊥AE于点F,利用待定系数法求得直线BE解析式,根据B由A点经n次斜平移得到进而求出B点坐标,最后利用S△ABC=S△ABE﹣S△ACE求出面积。
14.【答案】
【解析】【解答】解:由题意可得阴影部分面积等于正方形面积的 ,即是 ,
5个这样的正方形重叠部分(阴影部分)的面积和为 ×4,
n个这样的正方形重叠部分(阴影部分)的面积和为 ×(n-1)= cm2.
【分析】根据题意可得出,阴影部分面积等于正方形面积的 ,已知两个正方形可得出一个阴影部分,则n个这样的正方形重叠部分为n-1阴影部分的和。
15.【答案】解:依题意:
且
【解析】【分析】利用关于原点对称的点的坐标特征列出方程,求解即可。
16.【答案】解:(1)如图:△A1B1C1为所求作的三角形;
(2)四边形BC1B1C是平行四边形
连结BB1,CC1,
∵点B与B1,点C与C1分别关于点O成中心对称,
∴OB= OB1,OC= OC1,
∴四边形BC1B1C是平行四边形.
【解析】【分析】(1)将点A、B、C分别绕点O按逆时针方向旋转180°,得出对应点,即可得出△A1B1C1;
(2)连结BC1、B1C,BB1,CC1,由(1)可得点B与B1,点C与C1分别关于点O成中心对称,继而得出OB=OB1,OC=OC1,可证明四边形BC1B1C是平行四边形.
17.【答案】(1)解:如图所示,△A1B1C1、△A2B2C2即为所求,其中C1的坐标为(﹣1,3),其中点C2的坐标为(﹣3,﹣1);
(2)直角;
【解析】【解答】解:(3)∵C1C22=BC12=22+42=20,BC22=22+62=40,
∴C1C22+BC12=BC22,
∴△BC1C2是直角三角形,
则外接圆的半径R= BC2= ×2 = .
故答案为:直角, .
【分析】(1)①将三个顶点分别向左平移2个单位得到其对应点,再顺次连接即可得;②将三个顶点分别以点A1为旋转中心,逆时针方向旋转90°得到对应点,再顺次连接即可得;(2)利用勾股定理及其逆定理(如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形)求解可得.
18.【答案】(1)解:如图所示,则△A1B1C1、△A2B2C2为所求作的三角形,
∴A1(-4,-1),B1(-2,0)
(2)解:点C经过的路径长:是以(0,3)为圆心,以CC2为直径的半圆,
由勾股定理得:CC2= ,
∴点C经过的路径长:
【解析】【分析】(1)根据点C移到点C1(﹣2,﹣4),可知向下平移了5个单位,分别作出A、B、C的对应点A1、B1、C1即可解决问题。
(2)根据中心对称的性质,作出A、B、C的对应点A2、B2、C2即可。
(3)利用勾股定理求出CC2的长,可得半径为2,根据圆的周长公式计算即可。
19.【答案】(1)旋转
(2)1
(3)∠BDF+∠CEF=2∠F
【解析】【解答】解:(1)旋转;
( 2 )∵AD=2,
∴DC=AC﹣AD=3﹣2=1;
( 3 )∵把△ADE沿DE翻折,得到△FDE,
∴∠ADE=∠FDE,∠AED=∠FED,
在△DEF中,∠F=180°﹣(∠FDE+∠FED);
由平角定义知,∠BDF=180°﹣∠FDA=180°﹣2∠FDE,
∠CEF=180°﹣∠FEA=180°﹣2∠FED,
∴∠BDF+∠CEF=180°﹣2∠FDE+180°﹣2∠FED=2[180°﹣(∠FDE+∠FED)]
∴∠BDF+∠CEF=2∠F.
【分析】(1)旋转变换是指一个图形围绕一个定点旋转一定的角度,得到另一个图形;于是可由平移得到全等变换;
(2)由平移的性质可知,AD=2,所以DC=AC-AD可求解;
(3)由轴对称的性质可得∠ADE=∠EDF,∠AED=∠FED,再结合三角形的内角和定理即可求解。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
23.2 中心对称基础知识测试题
一、单选题
1.随着国民经济快速发展,我国涌现出一批规模大、效益高的企业,如大疆、国家核电、华为、凤凰光学等,以上四个企业的标志是中心对称图形的是( )
A. B.
C. D.
2.下列汽车标志中既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
3.下面的图形既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
4.在平面直角坐标系 中,点 的坐标是 ,连接 ,将线段 绕原点 旋转 ,得到对应线段 ,则点 的坐标是( )
A. B. C. D.
5.下列图形中,是中心对称图形的是( )
A. B.
C. D.
6.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
7.剪纸是中国的传统文化之一,剪纸图案中一般蕴含着对称美,下列图案中既是中心对称图形又是轴对称图形的是( )
A. B.
C. D.
8.在下列四个图案中,不是中心对称图形的是( )个
A. B. C. D.
9.如图,将先向下平移1个单位,再绕点按顺时针方向旋转一定角度,得到,顶点落到了点处,则点的对应点的坐标是( )
A. B. C. D.
10.围棋起源于中国.古代称之为“弈”,至今已有4000多年历史.2017年5月,世界围棋冠军柯洁与人工智能机器人AlphaGo进行了围棋人机大战.截取对战机棋谱中的四个部分,由黑白棋子摆成的图案是中心对称图形的是( )
A. B.
C. D.
11.如图,在平面直角坐标系中,点A的坐标是,点B的坐标为,点C的坐标为,将向左平移个单位长度后,再绕点O旋转,当垂直于x轴时,点B的对应点的坐标为( )
A.或 B.或
C.或 D.或
12.在下列命题中,正确的是( )
A.正多边形一个内角与一个外角相等,则它是正六边形
B.正多边形都是中心对称图形
C.边数大于3的正多边形的对角线长都相等
D.正多边形的一个外角为 ,则它是正十边形
13.对于坐标平面内的点,先将该点向右平移1个单位,再向上平移2个单位,这种点的运动称为点的斜平移,如点P(2,3)经1次斜平移后的点的坐标为(3,5).已知点A的坐标为(2,0),点Q是直线l上的一点,点A关于点Q的对称点为点B,点B关于直线l的对称点为点C,若点B由点A经n次斜平移后得到,且点C的坐标为(8,6),则△ABC的面积是( )
A.12 B.14 C.16 D.18
二、填空题
14.如图,将n个边长都为1cm的正方形按如图所示摆放,点A1, A2,…,An分别是正方形的中心,则n个正方形重叠形成的重叠部分的面积和为
三、计算题
15.已知点P(2x,y2+4)与Q(x2+1,-4y)关于原点对称,求x+y的值。
四、解答题
16.如图,在边长为1个单位长度的小正方形组成的方格中,点A、B、C都是格点.
(1)将△ABC绕点O按逆时针方向旋转180°得到△A1B1C1,请画出△A1B1C1;
(2)依次连结BC1、B1C,猜想四边形BC1B1C是什么特殊四边形 并说明理由.
五、作图题
17.如图,在平面直角坐标系中,已知A(2,0)、B(3,1)、C(1,3).
(1)①将△ABC沿x轴负方向移动2个单位长度至△A1B1C1,画图并写出点C1的坐标;
②以点A1为旋转中心,将△A1B1C1逆时针方向旋转90°得到△A2B2C2,画图并写出点C2的坐标;
(2)以B、C1、C2为顶点的三角形是 三角形,其外接圆的半径R= .
六、综合题
18.如图,△ABC在平面直角坐标系内,顶点的坐标分别为A(﹣4,4),B(﹣2,5),C(﹣2,1).
(1)①平移△ABC,使点C移到点C1(﹣2,﹣4),画出平移后的△A1B1C1,并写出点A1,B1的坐标;
②将△ABC绕点(0,3)旋转180°,得到△A2B2C2,画出旋转后的△A2B2C2;
(2)求(1)②中的点C旋转到点C2时,点C经过的路径长(结果保留π).
七、实践探究题
19.阅读材料,并回答下列问题:
如图1,以AB为轴,把△ABC翻折180°,可以变换到△ABD的位置;如图2,把△ABC沿射线AC平移,可以变换到△DEF的位置.像这样,其中的一个三角形是另一个三角形经翻折、平移等方法变换成的,这种只改变位置,不改变形状大小的图形变换,叫三角形的全等变换.
(1)请你写出一种全等变换的方法(除翻折、平移外). ;
(2)如图2,△ABC沿射线AC平移到△DEF,若平移的距离为2,且AC=3,则DC= ;
(3)如图3,D、E分别是△ABC的边AB、AC上的点,把△ADE沿DE翻折,当点A落在四边形BCED内部变为F时,则∠F和∠BDF+∠CEF之间的数量关系始终保持不变,请你直接写出它们之间的关系式: .
答案解析部分
1.【答案】B
【解析】【分析】在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,据此依次判断即可.
2.【答案】C
【解析】【解答】解:A是轴对称图形,B既不是轴对称图形也不是中心对称图形,C既是轴对称图形又是中心对称图形,D是轴对称图形.故答案为:C.
【分析】把一个平面图形,沿着某一条直线折叠,直线两旁的部分能完全重合的平面图形就是轴对称图形;把一个平面图像绕着某一点旋转180°后能与自身重合的图形就是中心对称图形,根据定义即可一一判断得出答案。
3.【答案】D
【解析】【解答】解:A.不是轴对称图形,是中心对称图形,故此选项不合题意;
B.是轴对称图形,不是中心对称图形,故此选项不合题意;
C.不是轴对称图形,也不是中心对称图形,故此选项不合题意;
D.是轴对称图形,也是中心对称图形,故此选项符合题意;
故答案为:D.
【分析】中心对称图形是图形绕某一点旋转180°后与原来的图形完全重合,轴对称图形是将一个图形沿某直线折叠后直线两旁的部分互相重合,再对各选项逐一判断.
4.【答案】A
【解析】【解答】解:如图,观察图象可知,B(2,-1).
故答案为:A.
【分析】 将线段 绕原点 旋转 得到对应线段 ,则OA与OB关于原点对称,于是根据关于原点对称的坐标特点即可得出B点坐标.
5.【答案】D
【解析】【解答】解:A、不是中心对称图形,故不符合题意;
B、不是中心对称图形,故不符合题意;
C、不是中心对称图形,故不符合题意;
D、是中心对称图形,故符合题意;
故答案为:D.
【分析】把一个平面图形,沿着某一点旋转180°后,能与自身重合的图形就是中心对称图形,根据定义即可一一判断得出答案.
6.【答案】D
【解析】【解答】解:A、不是轴对称图形,也不是中心对称图形,故本选项错误;
B、是轴对称图形,不是中心对称图形,故本选项错误;
C、不是轴对称图形,是中心对称图形,故本选项错误;
D、是轴对称图形,也是中心对称图形,故本选项正确.
故答案为:D.
【分析】中心对称图形是图形绕某一点旋转180°后与原来的图形完全重合;轴对称图形是将一个图形沿某直线折叠后直线两旁的部分互相重合,据此再对各选项逐一判断.
7.【答案】A
【解析】【解答】解:A.既是轴对称图形,又是中心对称图形,故本选项符合题意;
B.是轴对称图形,不是中心对称图形,故本选项不符合题意;
C.是轴对称图形,不是中心对称图形,故本选项不符合题意;
D.不是轴对称图形,是中心对称图形,故本选项不符合题意.
故答案为:A.
【分析】根据轴对称图形和中心对称图形的定义逐项判断即可。
8.【答案】D
【解析】【解答】解:A、.是中心对称图形,故不符合题意;
B、是中心对称图形,故不符合题意;
C、 是中心对称图形,故不符合题意;
D、不是中心对称图形,符合题意.
故答案为:D.
【分析】中心对称图形,就是一个图形绕一个中心旋转180°后,能与原来的图形完全重合的图形,根据定义分别判断即可.
9.【答案】C
【解析】【解答】解:如图,点的对应点的坐标是,
故答案为:C.
【分析】根据点坐标平移及旋转的特征求解即可。
10.【答案】D
【解析】【解答】解:A中图形不是中心对称图形,不符合题意;
B中图形不是中心对称图形,不符合题意;
C中图形不是中心对称图形,不符合题意;
D中图形是中心对称图形,符合题意;
故答案为:D.
【分析】根据中心对称图形的定义逐项判断即可。
11.【答案】D
【解析】【解答】解:如图,将向左平移个单位长度后,得到,
将绕点O逆时针旋转90°后,得到,此时B1C1⊥x轴,
∵C′(0,3),∴C1(-3,0),∵B1C1=,∴B1(-3,-);
将绕点O顺时针旋转90°后,得到,此时B2C2⊥x轴,
∵C′(0,3),∴C2(3,0),∵B2C2=,∴B2(3,);
∴点B的对应点的坐标为(-3,-)或(3,);
故答案为:D.
【分析】根据点坐标平移和点坐标旋转的性质求解即可。
12.【答案】D
【解析】【解答】A.正多边形一个内角与一个外角相等,则它是正六边形,故本选项错误;
B.正多边形不一定是中心对称图形,故本选项错误;
C.边数大于3的正多边形的对角线长不一定相等,故本选项错误;
D.正多边形的一个外角为 ,则它是正十边形,故本选项正确.
故答案为:D.
【分析】分析是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案.
13.【答案】A
【解析】【解答】解:连接CQ,如图:
由中心对称可知,AQ=BQ,
由轴对称可知:BQ=CQ,
∴AQ=CQ=BQ,
∴∠QAC=∠ACQ,∠QBC=∠QCB,
∵∠QAC+∠ACQ+∠QBC+∠QCB=180°,
∴∠ACQ+∠QCB=90°,
∴∠ACB=90°,
∴△ABC是直角三角形,
延长BC交x轴于点E,过C点作CF⊥AE于点F,如图,
∵A(2,0),C(8,6),
∴AF=CF=6,
∴△ACF是等腰直角三角形,
∵,
∴∠AEC=45°,
∴E点坐标为(14,0),
设直线BE的解析式为y=kx+b,
∵C,E点在直线上,
可得:,
解得:,
∴y=﹣x+14,
∵点B由点A经n次斜平移得到,
∴点B(n+2,2n),由2n=﹣n﹣2+14,
解得:n=4,
∴B(6,8),
∴△ABC的面积=S△ABE﹣S△ACE=×12×8﹣×12×6=12,
故答案为:A.
【分析】连接CQ,根据中心对称性质得AQ=BQ,由轴对称性质得BQ=CQ,利用斜边中线性质定理逆定理可判定△ABC为直角三角形,即∠ACB=90°;延长BC交x轴于点E,过C点作CF⊥AE于点F,利用待定系数法求得直线BE解析式,根据B由A点经n次斜平移得到进而求出B点坐标,最后利用S△ABC=S△ABE﹣S△ACE求出面积。
14.【答案】
【解析】【解答】解:由题意可得阴影部分面积等于正方形面积的 ,即是 ,
5个这样的正方形重叠部分(阴影部分)的面积和为 ×4,
n个这样的正方形重叠部分(阴影部分)的面积和为 ×(n-1)= cm2.
【分析】根据题意可得出,阴影部分面积等于正方形面积的 ,已知两个正方形可得出一个阴影部分,则n个这样的正方形重叠部分为n-1阴影部分的和。
15.【答案】解:依题意:
且
【解析】【分析】利用关于原点对称的点的坐标特征列出方程,求解即可。
16.【答案】解:(1)如图:△A1B1C1为所求作的三角形;
(2)四边形BC1B1C是平行四边形
连结BB1,CC1,
∵点B与B1,点C与C1分别关于点O成中心对称,
∴OB= OB1,OC= OC1,
∴四边形BC1B1C是平行四边形.
【解析】【分析】(1)将点A、B、C分别绕点O按逆时针方向旋转180°,得出对应点,即可得出△A1B1C1;
(2)连结BC1、B1C,BB1,CC1,由(1)可得点B与B1,点C与C1分别关于点O成中心对称,继而得出OB=OB1,OC=OC1,可证明四边形BC1B1C是平行四边形.
17.【答案】(1)解:如图所示,△A1B1C1、△A2B2C2即为所求,其中C1的坐标为(﹣1,3),其中点C2的坐标为(﹣3,﹣1);
(2)直角;
【解析】【解答】解:(3)∵C1C22=BC12=22+42=20,BC22=22+62=40,
∴C1C22+BC12=BC22,
∴△BC1C2是直角三角形,
则外接圆的半径R= BC2= ×2 = .
故答案为:直角, .
【分析】(1)①将三个顶点分别向左平移2个单位得到其对应点,再顺次连接即可得;②将三个顶点分别以点A1为旋转中心,逆时针方向旋转90°得到对应点,再顺次连接即可得;(2)利用勾股定理及其逆定理(如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形)求解可得.
18.【答案】(1)解:如图所示,则△A1B1C1、△A2B2C2为所求作的三角形,
∴A1(-4,-1),B1(-2,0)
(2)解:点C经过的路径长:是以(0,3)为圆心,以CC2为直径的半圆,
由勾股定理得:CC2= ,
∴点C经过的路径长:
【解析】【分析】(1)根据点C移到点C1(﹣2,﹣4),可知向下平移了5个单位,分别作出A、B、C的对应点A1、B1、C1即可解决问题。
(2)根据中心对称的性质,作出A、B、C的对应点A2、B2、C2即可。
(3)利用勾股定理求出CC2的长,可得半径为2,根据圆的周长公式计算即可。
19.【答案】(1)旋转
(2)1
(3)∠BDF+∠CEF=2∠F
【解析】【解答】解:(1)旋转;
( 2 )∵AD=2,
∴DC=AC﹣AD=3﹣2=1;
( 3 )∵把△ADE沿DE翻折,得到△FDE,
∴∠ADE=∠FDE,∠AED=∠FED,
在△DEF中,∠F=180°﹣(∠FDE+∠FED);
由平角定义知,∠BDF=180°﹣∠FDA=180°﹣2∠FDE,
∠CEF=180°﹣∠FEA=180°﹣2∠FED,
∴∠BDF+∠CEF=180°﹣2∠FDE+180°﹣2∠FED=2[180°﹣(∠FDE+∠FED)]
∴∠BDF+∠CEF=2∠F.
【分析】(1)旋转变换是指一个图形围绕一个定点旋转一定的角度,得到另一个图形;于是可由平移得到全等变换;
(2)由平移的性质可知,AD=2,所以DC=AC-AD可求解;
(3)由轴对称的性质可得∠ADE=∠EDF,∠AED=∠FED,再结合三角形的内角和定理即可求解。
23.2 中心对称基础知识测试题
一、单选题
1.随着国民经济快速发展,我国涌现出一批规模大、效益高的企业,如大疆、国家核电、华为、凤凰光学等,以上四个企业的标志是中心对称图形的是( )
A. B.
C. D.
2.下列汽车标志中既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
3.下面的图形既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
4.在平面直角坐标系 中,点 的坐标是 ,连接 ,将线段 绕原点 旋转 ,得到对应线段 ,则点 的坐标是( )
A. B. C. D.
5.下列图形中,是中心对称图形的是( )
A. B.
C. D.
6.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
7.剪纸是中国的传统文化之一,剪纸图案中一般蕴含着对称美,下列图案中既是中心对称图形又是轴对称图形的是( )
A. B.
C. D.
8.在下列四个图案中,不是中心对称图形的是( )个
A. B. C. D.
9.如图,将先向下平移1个单位,再绕点按顺时针方向旋转一定角度,得到,顶点落到了点处,则点的对应点的坐标是( )
A. B. C. D.
10.围棋起源于中国.古代称之为“弈”,至今已有4000多年历史.2017年5月,世界围棋冠军柯洁与人工智能机器人AlphaGo进行了围棋人机大战.截取对战机棋谱中的四个部分,由黑白棋子摆成的图案是中心对称图形的是( )
A. B.
C. D.
11.如图,在平面直角坐标系中,点A的坐标是,点B的坐标为,点C的坐标为,将向左平移个单位长度后,再绕点O旋转,当垂直于x轴时,点B的对应点的坐标为( )
A.或 B.或
C.或 D.或
12.在下列命题中,正确的是( )
A.正多边形一个内角与一个外角相等,则它是正六边形
B.正多边形都是中心对称图形
C.边数大于3的正多边形的对角线长都相等
D.正多边形的一个外角为 ,则它是正十边形
13.对于坐标平面内的点,先将该点向右平移1个单位,再向上平移2个单位,这种点的运动称为点的斜平移,如点P(2,3)经1次斜平移后的点的坐标为(3,5).已知点A的坐标为(2,0),点Q是直线l上的一点,点A关于点Q的对称点为点B,点B关于直线l的对称点为点C,若点B由点A经n次斜平移后得到,且点C的坐标为(8,6),则△ABC的面积是( )
A.12 B.14 C.16 D.18
二、填空题
14.如图,将n个边长都为1cm的正方形按如图所示摆放,点A1, A2,…,An分别是正方形的中心,则n个正方形重叠形成的重叠部分的面积和为
三、计算题
15.已知点P(2x,y2+4)与Q(x2+1,-4y)关于原点对称,求x+y的值。
四、解答题
16.如图,在边长为1个单位长度的小正方形组成的方格中,点A、B、C都是格点.
(1)将△ABC绕点O按逆时针方向旋转180°得到△A1B1C1,请画出△A1B1C1;
(2)依次连结BC1、B1C,猜想四边形BC1B1C是什么特殊四边形 并说明理由.
五、作图题
17.如图,在平面直角坐标系中,已知A(2,0)、B(3,1)、C(1,3).
(1)①将△ABC沿x轴负方向移动2个单位长度至△A1B1C1,画图并写出点C1的坐标;
②以点A1为旋转中心,将△A1B1C1逆时针方向旋转90°得到△A2B2C2,画图并写出点C2的坐标;
(2)以B、C1、C2为顶点的三角形是 三角形,其外接圆的半径R= .
六、综合题
18.如图,△ABC在平面直角坐标系内,顶点的坐标分别为A(﹣4,4),B(﹣2,5),C(﹣2,1).
(1)①平移△ABC,使点C移到点C1(﹣2,﹣4),画出平移后的△A1B1C1,并写出点A1,B1的坐标;
②将△ABC绕点(0,3)旋转180°,得到△A2B2C2,画出旋转后的△A2B2C2;
(2)求(1)②中的点C旋转到点C2时,点C经过的路径长(结果保留π).
七、实践探究题
19.阅读材料,并回答下列问题:
如图1,以AB为轴,把△ABC翻折180°,可以变换到△ABD的位置;如图2,把△ABC沿射线AC平移,可以变换到△DEF的位置.像这样,其中的一个三角形是另一个三角形经翻折、平移等方法变换成的,这种只改变位置,不改变形状大小的图形变换,叫三角形的全等变换.
(1)请你写出一种全等变换的方法(除翻折、平移外). ;
(2)如图2,△ABC沿射线AC平移到△DEF,若平移的距离为2,且AC=3,则DC= ;
(3)如图3,D、E分别是△ABC的边AB、AC上的点,把△ADE沿DE翻折,当点A落在四边形BCED内部变为F时,则∠F和∠BDF+∠CEF之间的数量关系始终保持不变,请你直接写出它们之间的关系式: .
答案解析部分
1.【答案】B
【解析】【分析】在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,据此依次判断即可.
2.【答案】C
【解析】【解答】解:A是轴对称图形,B既不是轴对称图形也不是中心对称图形,C既是轴对称图形又是中心对称图形,D是轴对称图形.故答案为:C.
【分析】把一个平面图形,沿着某一条直线折叠,直线两旁的部分能完全重合的平面图形就是轴对称图形;把一个平面图像绕着某一点旋转180°后能与自身重合的图形就是中心对称图形,根据定义即可一一判断得出答案。
3.【答案】D
【解析】【解答】解:A.不是轴对称图形,是中心对称图形,故此选项不合题意;
B.是轴对称图形,不是中心对称图形,故此选项不合题意;
C.不是轴对称图形,也不是中心对称图形,故此选项不合题意;
D.是轴对称图形,也是中心对称图形,故此选项符合题意;
故答案为:D.
【分析】中心对称图形是图形绕某一点旋转180°后与原来的图形完全重合,轴对称图形是将一个图形沿某直线折叠后直线两旁的部分互相重合,再对各选项逐一判断.
4.【答案】A
【解析】【解答】解:如图,观察图象可知,B(2,-1).
故答案为:A.
【分析】 将线段 绕原点 旋转 得到对应线段 ,则OA与OB关于原点对称,于是根据关于原点对称的坐标特点即可得出B点坐标.
5.【答案】D
【解析】【解答】解:A、不是中心对称图形,故不符合题意;
B、不是中心对称图形,故不符合题意;
C、不是中心对称图形,故不符合题意;
D、是中心对称图形,故符合题意;
故答案为:D.
【分析】把一个平面图形,沿着某一点旋转180°后,能与自身重合的图形就是中心对称图形,根据定义即可一一判断得出答案.
6.【答案】D
【解析】【解答】解:A、不是轴对称图形,也不是中心对称图形,故本选项错误;
B、是轴对称图形,不是中心对称图形,故本选项错误;
C、不是轴对称图形,是中心对称图形,故本选项错误;
D、是轴对称图形,也是中心对称图形,故本选项正确.
故答案为:D.
【分析】中心对称图形是图形绕某一点旋转180°后与原来的图形完全重合;轴对称图形是将一个图形沿某直线折叠后直线两旁的部分互相重合,据此再对各选项逐一判断.
7.【答案】A
【解析】【解答】解:A.既是轴对称图形,又是中心对称图形,故本选项符合题意;
B.是轴对称图形,不是中心对称图形,故本选项不符合题意;
C.是轴对称图形,不是中心对称图形,故本选项不符合题意;
D.不是轴对称图形,是中心对称图形,故本选项不符合题意.
故答案为:A.
【分析】根据轴对称图形和中心对称图形的定义逐项判断即可。
8.【答案】D
【解析】【解答】解:A、.是中心对称图形,故不符合题意;
B、是中心对称图形,故不符合题意;
C、 是中心对称图形,故不符合题意;
D、不是中心对称图形,符合题意.
故答案为:D.
【分析】中心对称图形,就是一个图形绕一个中心旋转180°后,能与原来的图形完全重合的图形,根据定义分别判断即可.
9.【答案】C
【解析】【解答】解:如图,点的对应点的坐标是,
故答案为:C.
【分析】根据点坐标平移及旋转的特征求解即可。
10.【答案】D
【解析】【解答】解:A中图形不是中心对称图形,不符合题意;
B中图形不是中心对称图形,不符合题意;
C中图形不是中心对称图形,不符合题意;
D中图形是中心对称图形,符合题意;
故答案为:D.
【分析】根据中心对称图形的定义逐项判断即可。
11.【答案】D
【解析】【解答】解:如图,将向左平移个单位长度后,得到,
将绕点O逆时针旋转90°后,得到,此时B1C1⊥x轴,
∵C′(0,3),∴C1(-3,0),∵B1C1=,∴B1(-3,-);
将绕点O顺时针旋转90°后,得到,此时B2C2⊥x轴,
∵C′(0,3),∴C2(3,0),∵B2C2=,∴B2(3,);
∴点B的对应点的坐标为(-3,-)或(3,);
故答案为:D.
【分析】根据点坐标平移和点坐标旋转的性质求解即可。
12.【答案】D
【解析】【解答】A.正多边形一个内角与一个外角相等,则它是正六边形,故本选项错误;
B.正多边形不一定是中心对称图形,故本选项错误;
C.边数大于3的正多边形的对角线长不一定相等,故本选项错误;
D.正多边形的一个外角为 ,则它是正十边形,故本选项正确.
故答案为:D.
【分析】分析是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案.
13.【答案】A
【解析】【解答】解:连接CQ,如图:
由中心对称可知,AQ=BQ,
由轴对称可知:BQ=CQ,
∴AQ=CQ=BQ,
∴∠QAC=∠ACQ,∠QBC=∠QCB,
∵∠QAC+∠ACQ+∠QBC+∠QCB=180°,
∴∠ACQ+∠QCB=90°,
∴∠ACB=90°,
∴△ABC是直角三角形,
延长BC交x轴于点E,过C点作CF⊥AE于点F,如图,
∵A(2,0),C(8,6),
∴AF=CF=6,
∴△ACF是等腰直角三角形,
∵,
∴∠AEC=45°,
∴E点坐标为(14,0),
设直线BE的解析式为y=kx+b,
∵C,E点在直线上,
可得:,
解得:,
∴y=﹣x+14,
∵点B由点A经n次斜平移得到,
∴点B(n+2,2n),由2n=﹣n﹣2+14,
解得:n=4,
∴B(6,8),
∴△ABC的面积=S△ABE﹣S△ACE=×12×8﹣×12×6=12,
故答案为:A.
【分析】连接CQ,根据中心对称性质得AQ=BQ,由轴对称性质得BQ=CQ,利用斜边中线性质定理逆定理可判定△ABC为直角三角形,即∠ACB=90°;延长BC交x轴于点E,过C点作CF⊥AE于点F,利用待定系数法求得直线BE解析式,根据B由A点经n次斜平移得到进而求出B点坐标,最后利用S△ABC=S△ABE﹣S△ACE求出面积。
14.【答案】
【解析】【解答】解:由题意可得阴影部分面积等于正方形面积的 ,即是 ,
5个这样的正方形重叠部分(阴影部分)的面积和为 ×4,
n个这样的正方形重叠部分(阴影部分)的面积和为 ×(n-1)= cm2.
【分析】根据题意可得出,阴影部分面积等于正方形面积的 ,已知两个正方形可得出一个阴影部分,则n个这样的正方形重叠部分为n-1阴影部分的和。
15.【答案】解:依题意:
且
【解析】【分析】利用关于原点对称的点的坐标特征列出方程,求解即可。
16.【答案】解:(1)如图:△A1B1C1为所求作的三角形;
(2)四边形BC1B1C是平行四边形
连结BB1,CC1,
∵点B与B1,点C与C1分别关于点O成中心对称,
∴OB= OB1,OC= OC1,
∴四边形BC1B1C是平行四边形.
【解析】【分析】(1)将点A、B、C分别绕点O按逆时针方向旋转180°,得出对应点,即可得出△A1B1C1;
(2)连结BC1、B1C,BB1,CC1,由(1)可得点B与B1,点C与C1分别关于点O成中心对称,继而得出OB=OB1,OC=OC1,可证明四边形BC1B1C是平行四边形.
17.【答案】(1)解:如图所示,△A1B1C1、△A2B2C2即为所求,其中C1的坐标为(﹣1,3),其中点C2的坐标为(﹣3,﹣1);
(2)直角;
【解析】【解答】解:(3)∵C1C22=BC12=22+42=20,BC22=22+62=40,
∴C1C22+BC12=BC22,
∴△BC1C2是直角三角形,
则外接圆的半径R= BC2= ×2 = .
故答案为:直角, .
【分析】(1)①将三个顶点分别向左平移2个单位得到其对应点,再顺次连接即可得;②将三个顶点分别以点A1为旋转中心,逆时针方向旋转90°得到对应点,再顺次连接即可得;(2)利用勾股定理及其逆定理(如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形)求解可得.
18.【答案】(1)解:如图所示,则△A1B1C1、△A2B2C2为所求作的三角形,
∴A1(-4,-1),B1(-2,0)
(2)解:点C经过的路径长:是以(0,3)为圆心,以CC2为直径的半圆,
由勾股定理得:CC2= ,
∴点C经过的路径长:
【解析】【分析】(1)根据点C移到点C1(﹣2,﹣4),可知向下平移了5个单位,分别作出A、B、C的对应点A1、B1、C1即可解决问题。
(2)根据中心对称的性质,作出A、B、C的对应点A2、B2、C2即可。
(3)利用勾股定理求出CC2的长,可得半径为2,根据圆的周长公式计算即可。
19.【答案】(1)旋转
(2)1
(3)∠BDF+∠CEF=2∠F
【解析】【解答】解:(1)旋转;
( 2 )∵AD=2,
∴DC=AC﹣AD=3﹣2=1;
( 3 )∵把△ADE沿DE翻折,得到△FDE,
∴∠ADE=∠FDE,∠AED=∠FED,
在△DEF中,∠F=180°﹣(∠FDE+∠FED);
由平角定义知,∠BDF=180°﹣∠FDA=180°﹣2∠FDE,
∠CEF=180°﹣∠FEA=180°﹣2∠FED,
∴∠BDF+∠CEF=180°﹣2∠FDE+180°﹣2∠FED=2[180°﹣(∠FDE+∠FED)]
∴∠BDF+∠CEF=2∠F.
【分析】(1)旋转变换是指一个图形围绕一个定点旋转一定的角度,得到另一个图形;于是可由平移得到全等变换;
(2)由平移的性质可知,AD=2,所以DC=AC-AD可求解;
(3)由轴对称的性质可得∠ADE=∠EDF,∠AED=∠FED,再结合三角形的内角和定理即可求解。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
