第十二章 三角形 全等三角形的基本模型(含解析)
文档属性
| 名称 | 第十二章 三角形 全等三角形的基本模型(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-24 14:38:30 | ||
图片预览

文档简介
第十二章 三角形 习题课 全等三角形的基本模型
【知识网络】
【同步练习】
类型1 平移模型
此模型的特征是有一组边共线或部分重合,另两组边分别平行,需要在移动方向上加(减)公共线段,构造线段相等,或利用平行线性质找到对应角相等.
1.如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF,∠A=40°,∠F=75°,则∠B= .
2.如图①,点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF.
(1)求证:△ABC≌△DEF;
(2)如图②,其他条件不变,△ABC≌△DEF还成立吗?试说明理由.
3. 如图,O是线段AB的中点,OD∥BC且OD=BC.
(1)求证:△AOD≌△OBC;
(2)若∠D=35°,求∠DOC的度数.
类型2 对称模型
所给图形可沿某一直线折叠,直线两旁的部分能完全重合,重合的顶点就是全等三角形的对应顶点,解题时要注意其隐含条件,即公共边或公共角相等.
4.如图,已知,BD平分∠ABC和∠ADC,若AB=3,则BC= .
5.如图,AC与BD相交于点O,AO=DO,∠B=∠C,AC=8,则BD= .
6.如图,∠A=∠D=90°,AC=DB,AC、DB相交于点O.求证:OB=OC.
7.如图,AB=AD,BC=DC,点E在AC上.求证:
(1)AC平分∠BAD;
(2)BE=DE.
类型3 旋转模型
8.如图,已知AE=AD,AB=AC,EC=DB,下列结论:①∠C=∠B;②∠D=∠E;③∠EAD=∠BAC;④∠B=∠E.其中错误的是 ( )
A.①② B.②③ C.③④ D.只有④
9.将两块全等的直角三角形如图①摆放,其中∠DCE=∠ACB=90°,∠D=∠A.
(1)求证:AB⊥DE;
(2)将图中的△DCE绕点C顺时针旋转45°得到图②,AB、CD交于点N,DE、BC交于M.求证:CM=CN.
10.复习“全等三角形”的知识时,老师布置了一道作业题:“如图①,在△ABC中,AB=AC,P是△ABC内任意一点,将AP绕点A顺时针旋转至AQ,使∠QAP=∠BAC,连接BQ,CP,则BQ=CP.”小亮是个爱动脑筋的同学,他通过对图①的分析,证明了△ABQ≌△ACP,从而证得BQ=CP.之后,他将点P移到△ABC外,原题中其他条件不变,发现“BQ=CP”仍然成立,请你就图②给出证明.
类型4 一线三等角模型
11.如图,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(-2,0),点A的坐标为(-6,3),则B点的坐标为 .
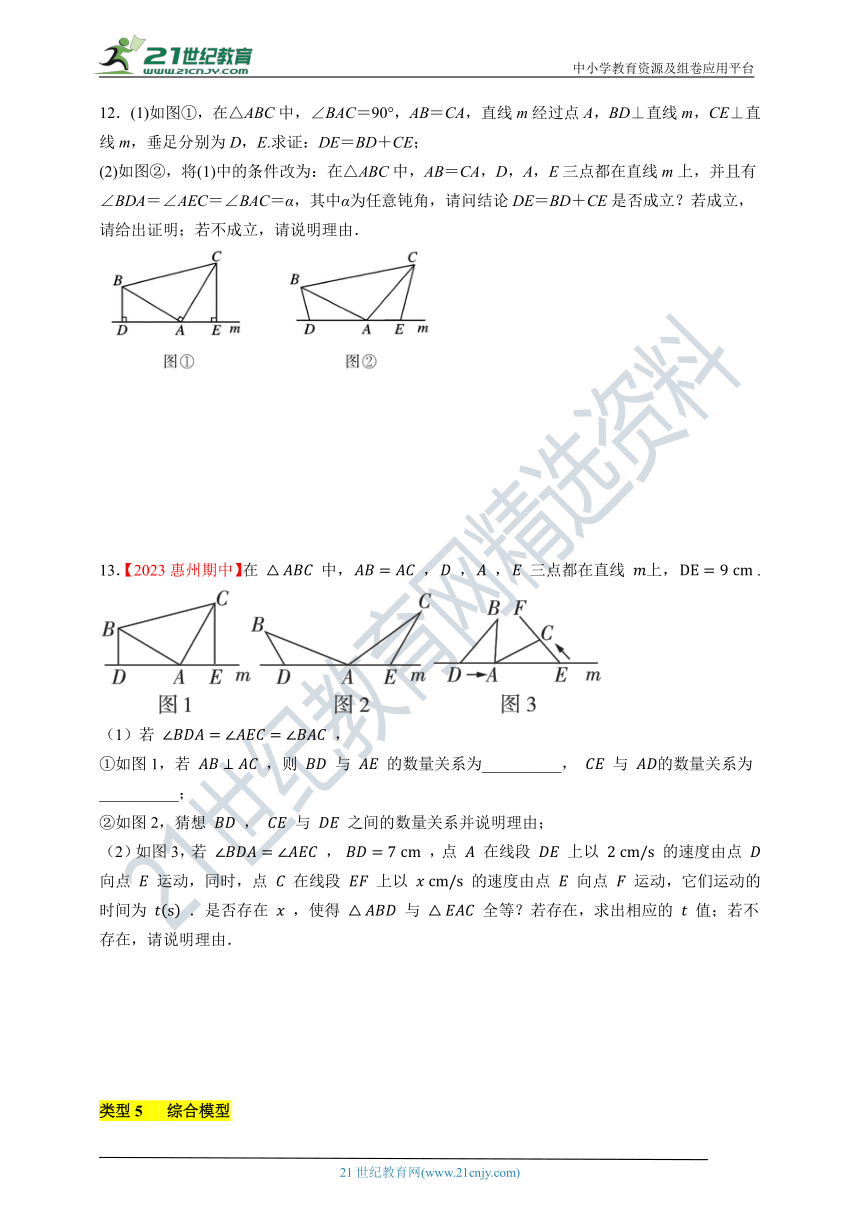
12.(1)如图①,在△ABC中,∠BAC=90°,AB=CA,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为D,E.求证:DE=BD+CE;
(2)如图②,将(1)中的条件改为:在△ABC中,AB=CA,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角,请问结论DE=BD+CE是否成立?若成立,请给出证明;若不成立,请说明理由.
13.【2023惠州期中】在 中, , , , 三点都在直线 上, .
(1)若 ,
①如图1,若 ,则 与 的数量关系为__________, 与 的数量关系为__________;
②如图2,猜想 , 与 之间的数量关系并说明理由;
(2)如图3,若 , ,点 在线段 上以 的速度由点 向点 运动,同时,点 在线段 上以 的速度由点 向点 运动,它们运动的时间为 .是否存在 ,使得 与 全等?若存在,求出相应的 值;若不存在,请说明理由.
类型5 综合模型
平移+旋转模型:
平移+对称模型:
14.如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,AD=7,BE=3.
(1)求证:△BEC≌△CDA;
(2)求△BDE的面积.
15.如图①,点A,B,C,D在同一直线上,AB=CD,DE∥AF,且DE=AF.
(1)求证:△AFC≌△DEB;
(2)如果将BD沿着AD边的方向平行移动至图②,③的位置时,其余条件不变,(1)中的结论是否依然成立?如果成立,请予以证明;如果不成立,请说明理由.
图① 图② 图③
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【同步练习】
类型1 平移模型
此模型的特征是有一组边共线或部分重合,另两组边分别平行,需要在移动方向上加(减)公共线段,构造线段相等,或利用平行线性质找到对应角相等.
1.如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF,∠A=40°,∠F=75°,则∠B= .
【答案】65°
2.如图①,点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF.
(1)求证:△ABC≌△DEF;
(2)如图②,其他条件不变,△ABC≌△DEF还成立吗?试说明理由.
(1)证明:∵BE=CF,∴BE+CE=CF+EC,∴BC=FE.在△ABC与△DEF中,∵AB=DE,AC=DF,BC=EF,∴△ABC≌△DEF;
(2)解:还成立.理由如下:∵BE=CF,∴BE-CE=CF-EC,∴BC=FE.在△ABC与△DEF中,∵AB=DE,AC=DF,BC=EF,∴△ABC≌△DEF.
3. 如图,O是线段AB的中点,OD∥BC且OD=BC.
(1)求证:△AOD≌△OBC;
(2)若∠D=35°,求∠DOC的度数.
解:(1)证明:∵O是线段AB的中点,∴AO=OB.
∵OD∥BC,∴∠AOD=∠B.
在△AOD和△OBC中,
∴△AOD≌△OBC(SAS).
(2)∵△AOD≌△OBC,∴∠D=∠C=35°.
∵OD∥BC,∴∠DOC=∠C=35°.
类型2 对称模型
所给图形可沿某一直线折叠,直线两旁的部分能完全重合,重合的顶点就是全等三角形的对应顶点,解题时要注意其隐含条件,即公共边或公共角相等.
4.如图,已知,BD平分∠ABC和∠ADC,若AB=3,则BC= .
【答案】3
5.如图,AC与BD相交于点O,AO=DO,∠B=∠C,AC=8,则BD= .
【答案】8
6.如图,∠A=∠D=90°,AC=DB,AC、DB相交于点O.求证:OB=OC.
证明:在Rt△ABC和Rt△DCB中,,∴Rt△ABC≌Rt△DCB(HL),∴AB=CD,∵∠AOB=∠DOC,∠A=∠D,∴△ABO≌△DCO(AAS),∴OB=OC.
7.如图,AB=AD,BC=DC,点E在AC上.求证:
(1)AC平分∠BAD;
(2)BE=DE.
证明:(1)在△ABC和△ADC中,
∴△ABC≌△ADC(SSS).
∴∠BAC=∠DAC.即AC平分∠BAD.
(2)由(1)知,∠BAE=∠DAE.
在△BAE和△DAE中,
∴△BAE≌△DAE(SAS).∴BE=DE.
类型3 旋转模型
8.如图,已知AE=AD,AB=AC,EC=DB,下列结论:①∠C=∠B;②∠D=∠E;③∠EAD=∠BAC;④∠B=∠E.其中错误的是 ( D )
A.①② B.②③ C.③④ D.只有④
9.将两块全等的直角三角形如图①摆放,其中∠DCE=∠ACB=90°,∠D=∠A.
(1)求证:AB⊥DE;
(2)将图中的△DCE绕点C顺时针旋转45°得到图②,AB、CD交于点N,DE、BC交于M.求证:CM=CN.
证明:(1)延长AB交DE于点F,∵∠A=∠D,∠CBA=∠DBF,∴∠DFB=∠ACB=90°,∴AB⊥DE;
(2)∵∠MCD=∠NCA=45°,∠A=∠D,CD=CA,∴△CMD≌△CNA(ASA),∴CM=CN.
10.复习“全等三角形”的知识时,老师布置了一道作业题:“如图①,在△ABC中,AB=AC,P是△ABC内任意一点,将AP绕点A顺时针旋转至AQ,使∠QAP=∠BAC,连接BQ,CP,则BQ=CP.”小亮是个爱动脑筋的同学,他通过对图①的分析,证明了△ABQ≌△ACP,从而证得BQ=CP.之后,他将点P移到△ABC外,原题中其他条件不变,发现“BQ=CP”仍然成立,请你就图②给出证明.
证明:∵∠QAP=∠BAC,
∴∠QAP+∠PAB=∠PAB+∠BAC,
即∠QAB=∠PAC.
在△ABQ和△ACP中,
∴△ABQ≌△ACP(SAS).∴BQ=CP.
类型4 一线三等角模型
11.如图,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(-2,0),点A的坐标为(-6,3),则B点的坐标为 .
【答案】(1,4)
12.(1)如图①,在△ABC中,∠BAC=90°,AB=CA,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为D,E.求证:DE=BD+CE;
(2)如图②,将(1)中的条件改为:在△ABC中,AB=CA,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角,请问结论DE=BD+CE是否成立?若成立,请给出证明;若不成立,请说明理由.
解:(1)证明:∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°.
∴∠BAD+∠ABD=90°.
∵∠BAC=90°,∴∠BAD+∠CAE=90°,
∴∠ABD=∠CAE.
在△ADB和△CEA中,
∴△ADB≌△CEA(AAS).
∴BD=AE,AD=CE.
∴DE=AE+AD=BD+CE.
(2)结论DE=BD+CE成立.
证明:∵∠BDA=∠BAC=α,
∠BAC+∠CAE=∠BDA+∠ABD,
∴∠ABD=∠CAE.
在△ADB和△CEA中,
∴△ADB≌△CEA(AAS).
∴BD=AE,AD=CE.
∴DE=AE+AD=BD+CE.
13.【2023惠州期中】在 中, , , , 三点都在直线 上, .
(1)若 ,
①如图1,若 ,则 与 的数量关系为__________, 与 的数量关系为__________;
【解析】 , , ,又 , , , , .
【答案】
②如图2,猜想 , 与 之间的数量关系并说明理由;
解: .理由如下:
由(1)同理可得 ,
, , .
(2)如图3,若 , ,点 在线段 上以 的速度由点 向点 运动,同时,点 在线段 上以 的速度由点 向点 运动,它们运动的时间为 .是否存在 ,使得 与 全等?若存在,求出相应的 值;若不存在,请说明理由.
解:存在.
当 时,
, ,
,此时 ;
当 时,
, ,
,此时 .综上,当 时, 或当 时, .
类型5 综合模型
平移+旋转模型:
平移+对称模型:
14.如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,AD=7,BE=3.
(1)求证:△BEC≌△CDA;
(2)求△BDE的面积.
(1)证明:∵∠ACB=90°,BE⊥CE,AD⊥CE,∴∠ADC=∠CEB,∠DAC=∠ECB,∵AC=BC,∴△BEC≌△CDA(AAS);
(2)解:由(1)得CD=BE=3,CE=AD=7,∴DE=CE-CD=4,∴S△BDE=×3×4=6.
15.如图①,点A,B,C,D在同一直线上,AB=CD,DE∥AF,且DE=AF.
(1)求证:△AFC≌△DEB;
(2)如果将BD沿着AD边的方向平行移动至图②,③的位置时,其余条件不变,(1)中的结论是否依然成立?如果成立,请予以证明;如果不成立,请说明理由.
图① 图② 图③
解:(1)证明:∵AB=CD,
∴AB+BC=CD+BC,即AC=BD.
∵DE∥AF,∴∠A=∠D.
在△AFC和△DEB中,
∴△AFC≌△DEB(SAS).
(2)在图②,③中结论依然成立.
证明:在图②中,∵DE∥AF,∴∠A=∠D.
在△AFC和△DEB中,
∴△AFC≌△DEB(SAS).
在图③中,∵AB=CD,
∴AB-BC=CD-BC,即AC=BD.
∵AF∥DE,∴∠A=∠D.
在△AFC和△DEB中,
∴△AFC≌△DEB(SAS).
【知识网络】
【同步练习】
类型1 平移模型
此模型的特征是有一组边共线或部分重合,另两组边分别平行,需要在移动方向上加(减)公共线段,构造线段相等,或利用平行线性质找到对应角相等.
1.如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF,∠A=40°,∠F=75°,则∠B= .
2.如图①,点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF.
(1)求证:△ABC≌△DEF;
(2)如图②,其他条件不变,△ABC≌△DEF还成立吗?试说明理由.
3. 如图,O是线段AB的中点,OD∥BC且OD=BC.
(1)求证:△AOD≌△OBC;
(2)若∠D=35°,求∠DOC的度数.
类型2 对称模型
所给图形可沿某一直线折叠,直线两旁的部分能完全重合,重合的顶点就是全等三角形的对应顶点,解题时要注意其隐含条件,即公共边或公共角相等.
4.如图,已知,BD平分∠ABC和∠ADC,若AB=3,则BC= .
5.如图,AC与BD相交于点O,AO=DO,∠B=∠C,AC=8,则BD= .
6.如图,∠A=∠D=90°,AC=DB,AC、DB相交于点O.求证:OB=OC.
7.如图,AB=AD,BC=DC,点E在AC上.求证:
(1)AC平分∠BAD;
(2)BE=DE.
类型3 旋转模型
8.如图,已知AE=AD,AB=AC,EC=DB,下列结论:①∠C=∠B;②∠D=∠E;③∠EAD=∠BAC;④∠B=∠E.其中错误的是 ( )
A.①② B.②③ C.③④ D.只有④
9.将两块全等的直角三角形如图①摆放,其中∠DCE=∠ACB=90°,∠D=∠A.
(1)求证:AB⊥DE;
(2)将图中的△DCE绕点C顺时针旋转45°得到图②,AB、CD交于点N,DE、BC交于M.求证:CM=CN.
10.复习“全等三角形”的知识时,老师布置了一道作业题:“如图①,在△ABC中,AB=AC,P是△ABC内任意一点,将AP绕点A顺时针旋转至AQ,使∠QAP=∠BAC,连接BQ,CP,则BQ=CP.”小亮是个爱动脑筋的同学,他通过对图①的分析,证明了△ABQ≌△ACP,从而证得BQ=CP.之后,他将点P移到△ABC外,原题中其他条件不变,发现“BQ=CP”仍然成立,请你就图②给出证明.
类型4 一线三等角模型
11.如图,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(-2,0),点A的坐标为(-6,3),则B点的坐标为 .
12.(1)如图①,在△ABC中,∠BAC=90°,AB=CA,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为D,E.求证:DE=BD+CE;
(2)如图②,将(1)中的条件改为:在△ABC中,AB=CA,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角,请问结论DE=BD+CE是否成立?若成立,请给出证明;若不成立,请说明理由.
13.【2023惠州期中】在 中, , , , 三点都在直线 上, .
(1)若 ,
①如图1,若 ,则 与 的数量关系为__________, 与 的数量关系为__________;
②如图2,猜想 , 与 之间的数量关系并说明理由;
(2)如图3,若 , ,点 在线段 上以 的速度由点 向点 运动,同时,点 在线段 上以 的速度由点 向点 运动,它们运动的时间为 .是否存在 ,使得 与 全等?若存在,求出相应的 值;若不存在,请说明理由.
类型5 综合模型
平移+旋转模型:
平移+对称模型:
14.如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,AD=7,BE=3.
(1)求证:△BEC≌△CDA;
(2)求△BDE的面积.
15.如图①,点A,B,C,D在同一直线上,AB=CD,DE∥AF,且DE=AF.
(1)求证:△AFC≌△DEB;
(2)如果将BD沿着AD边的方向平行移动至图②,③的位置时,其余条件不变,(1)中的结论是否依然成立?如果成立,请予以证明;如果不成立,请说明理由.
图① 图② 图③
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
【同步练习】
类型1 平移模型
此模型的特征是有一组边共线或部分重合,另两组边分别平行,需要在移动方向上加(减)公共线段,构造线段相等,或利用平行线性质找到对应角相等.
1.如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF,∠A=40°,∠F=75°,则∠B= .
【答案】65°
2.如图①,点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF.
(1)求证:△ABC≌△DEF;
(2)如图②,其他条件不变,△ABC≌△DEF还成立吗?试说明理由.
(1)证明:∵BE=CF,∴BE+CE=CF+EC,∴BC=FE.在△ABC与△DEF中,∵AB=DE,AC=DF,BC=EF,∴△ABC≌△DEF;
(2)解:还成立.理由如下:∵BE=CF,∴BE-CE=CF-EC,∴BC=FE.在△ABC与△DEF中,∵AB=DE,AC=DF,BC=EF,∴△ABC≌△DEF.
3. 如图,O是线段AB的中点,OD∥BC且OD=BC.
(1)求证:△AOD≌△OBC;
(2)若∠D=35°,求∠DOC的度数.
解:(1)证明:∵O是线段AB的中点,∴AO=OB.
∵OD∥BC,∴∠AOD=∠B.
在△AOD和△OBC中,
∴△AOD≌△OBC(SAS).
(2)∵△AOD≌△OBC,∴∠D=∠C=35°.
∵OD∥BC,∴∠DOC=∠C=35°.
类型2 对称模型
所给图形可沿某一直线折叠,直线两旁的部分能完全重合,重合的顶点就是全等三角形的对应顶点,解题时要注意其隐含条件,即公共边或公共角相等.
4.如图,已知,BD平分∠ABC和∠ADC,若AB=3,则BC= .
【答案】3
5.如图,AC与BD相交于点O,AO=DO,∠B=∠C,AC=8,则BD= .
【答案】8
6.如图,∠A=∠D=90°,AC=DB,AC、DB相交于点O.求证:OB=OC.
证明:在Rt△ABC和Rt△DCB中,,∴Rt△ABC≌Rt△DCB(HL),∴AB=CD,∵∠AOB=∠DOC,∠A=∠D,∴△ABO≌△DCO(AAS),∴OB=OC.
7.如图,AB=AD,BC=DC,点E在AC上.求证:
(1)AC平分∠BAD;
(2)BE=DE.
证明:(1)在△ABC和△ADC中,
∴△ABC≌△ADC(SSS).
∴∠BAC=∠DAC.即AC平分∠BAD.
(2)由(1)知,∠BAE=∠DAE.
在△BAE和△DAE中,
∴△BAE≌△DAE(SAS).∴BE=DE.
类型3 旋转模型
8.如图,已知AE=AD,AB=AC,EC=DB,下列结论:①∠C=∠B;②∠D=∠E;③∠EAD=∠BAC;④∠B=∠E.其中错误的是 ( D )
A.①② B.②③ C.③④ D.只有④
9.将两块全等的直角三角形如图①摆放,其中∠DCE=∠ACB=90°,∠D=∠A.
(1)求证:AB⊥DE;
(2)将图中的△DCE绕点C顺时针旋转45°得到图②,AB、CD交于点N,DE、BC交于M.求证:CM=CN.
证明:(1)延长AB交DE于点F,∵∠A=∠D,∠CBA=∠DBF,∴∠DFB=∠ACB=90°,∴AB⊥DE;
(2)∵∠MCD=∠NCA=45°,∠A=∠D,CD=CA,∴△CMD≌△CNA(ASA),∴CM=CN.
10.复习“全等三角形”的知识时,老师布置了一道作业题:“如图①,在△ABC中,AB=AC,P是△ABC内任意一点,将AP绕点A顺时针旋转至AQ,使∠QAP=∠BAC,连接BQ,CP,则BQ=CP.”小亮是个爱动脑筋的同学,他通过对图①的分析,证明了△ABQ≌△ACP,从而证得BQ=CP.之后,他将点P移到△ABC外,原题中其他条件不变,发现“BQ=CP”仍然成立,请你就图②给出证明.
证明:∵∠QAP=∠BAC,
∴∠QAP+∠PAB=∠PAB+∠BAC,
即∠QAB=∠PAC.
在△ABQ和△ACP中,
∴△ABQ≌△ACP(SAS).∴BQ=CP.
类型4 一线三等角模型
11.如图,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(-2,0),点A的坐标为(-6,3),则B点的坐标为 .
【答案】(1,4)
12.(1)如图①,在△ABC中,∠BAC=90°,AB=CA,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为D,E.求证:DE=BD+CE;
(2)如图②,将(1)中的条件改为:在△ABC中,AB=CA,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角,请问结论DE=BD+CE是否成立?若成立,请给出证明;若不成立,请说明理由.
解:(1)证明:∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°.
∴∠BAD+∠ABD=90°.
∵∠BAC=90°,∴∠BAD+∠CAE=90°,
∴∠ABD=∠CAE.
在△ADB和△CEA中,
∴△ADB≌△CEA(AAS).
∴BD=AE,AD=CE.
∴DE=AE+AD=BD+CE.
(2)结论DE=BD+CE成立.
证明:∵∠BDA=∠BAC=α,
∠BAC+∠CAE=∠BDA+∠ABD,
∴∠ABD=∠CAE.
在△ADB和△CEA中,
∴△ADB≌△CEA(AAS).
∴BD=AE,AD=CE.
∴DE=AE+AD=BD+CE.
13.【2023惠州期中】在 中, , , , 三点都在直线 上, .
(1)若 ,
①如图1,若 ,则 与 的数量关系为__________, 与 的数量关系为__________;
【解析】 , , ,又 , , , , .
【答案】
②如图2,猜想 , 与 之间的数量关系并说明理由;
解: .理由如下:
由(1)同理可得 ,
, , .
(2)如图3,若 , ,点 在线段 上以 的速度由点 向点 运动,同时,点 在线段 上以 的速度由点 向点 运动,它们运动的时间为 .是否存在 ,使得 与 全等?若存在,求出相应的 值;若不存在,请说明理由.
解:存在.
当 时,
, ,
,此时 ;
当 时,
, ,
,此时 .综上,当 时, 或当 时, .
类型5 综合模型
平移+旋转模型:
平移+对称模型:
14.如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,AD=7,BE=3.
(1)求证:△BEC≌△CDA;
(2)求△BDE的面积.
(1)证明:∵∠ACB=90°,BE⊥CE,AD⊥CE,∴∠ADC=∠CEB,∠DAC=∠ECB,∵AC=BC,∴△BEC≌△CDA(AAS);
(2)解:由(1)得CD=BE=3,CE=AD=7,∴DE=CE-CD=4,∴S△BDE=×3×4=6.
15.如图①,点A,B,C,D在同一直线上,AB=CD,DE∥AF,且DE=AF.
(1)求证:△AFC≌△DEB;
(2)如果将BD沿着AD边的方向平行移动至图②,③的位置时,其余条件不变,(1)中的结论是否依然成立?如果成立,请予以证明;如果不成立,请说明理由.
图① 图② 图③
解:(1)证明:∵AB=CD,
∴AB+BC=CD+BC,即AC=BD.
∵DE∥AF,∴∠A=∠D.
在△AFC和△DEB中,
∴△AFC≌△DEB(SAS).
(2)在图②,③中结论依然成立.
证明:在图②中,∵DE∥AF,∴∠A=∠D.
在△AFC和△DEB中,
∴△AFC≌△DEB(SAS).
在图③中,∵AB=CD,
∴AB-BC=CD-BC,即AC=BD.
∵AF∥DE,∴∠A=∠D.
在△AFC和△DEB中,
∴△AFC≌△DEB(SAS).
