轴对称再认识(一)(同步练习)-五年级上册数学 北师大版(含解析)
文档属性
| 名称 | 轴对称再认识(一)(同步练习)-五年级上册数学 北师大版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 276.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-24 14:20:09 | ||
图片预览


文档简介
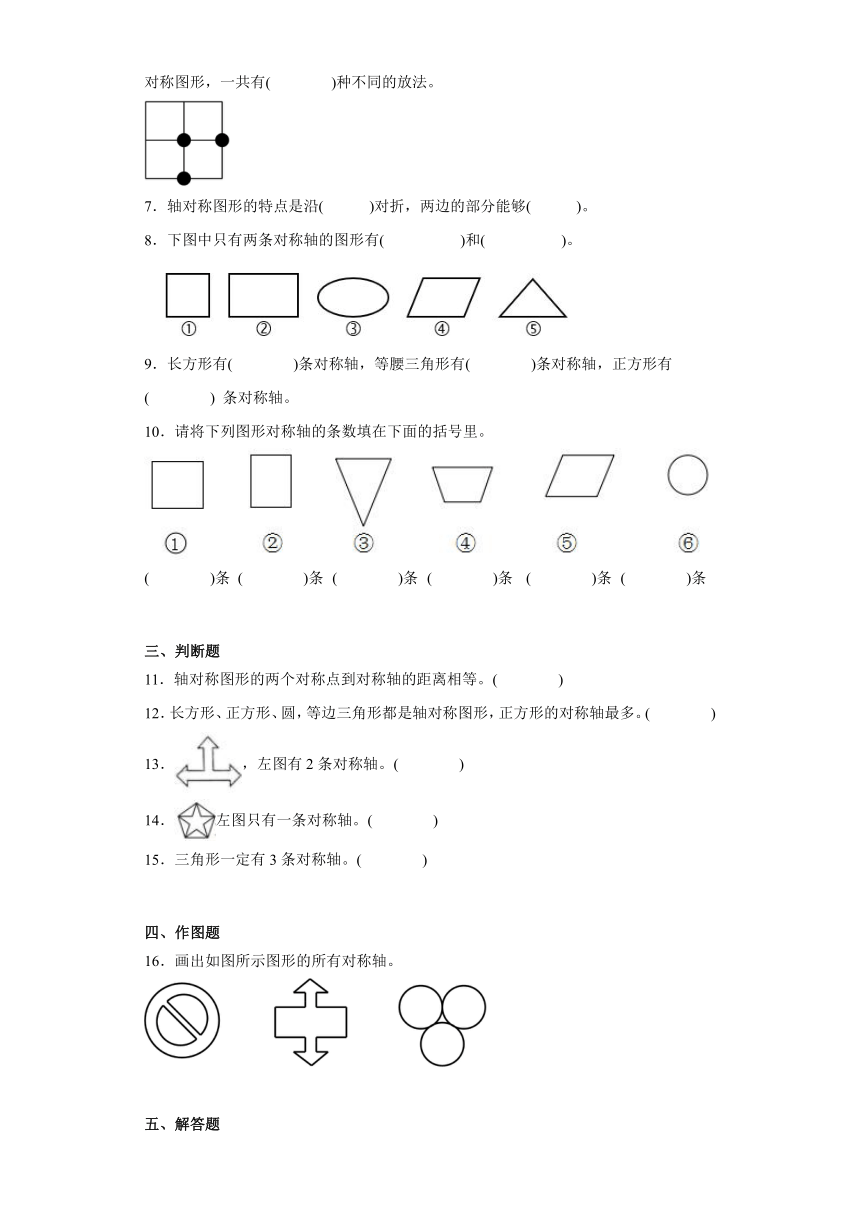
23年秋学期北师大版数学五年级上册第二单元《轴对称和平移》——《轴对称再认识(一)》课后练习一
学校:___________姓名:___________班级:___________
一、选择题
1.下面图形中,对称轴最多的是( )。
A.等边三角形 B.等腰梯形 C.长方形 D.正方形
2.下面的图案中,是轴对称图形的有( )个。
A.4 B.3 C.2 D.1
3.将一张正方形纸按下图所示的方式两次折叠,折叠后再按图所示沿MN剪开,则可得( )。
A.多个等腰直角三角形 B.一个等腰直角三角形和一个正方形
C.四个相同的正方形 D.两个相同的正方形
4.如图所示的标志中不是轴对称图形的是( )。
A. B. C. D.
5.下图是小明在镜子中看见身后墙上的钟,时间最接近8时的是( )。
A. B. C. D.
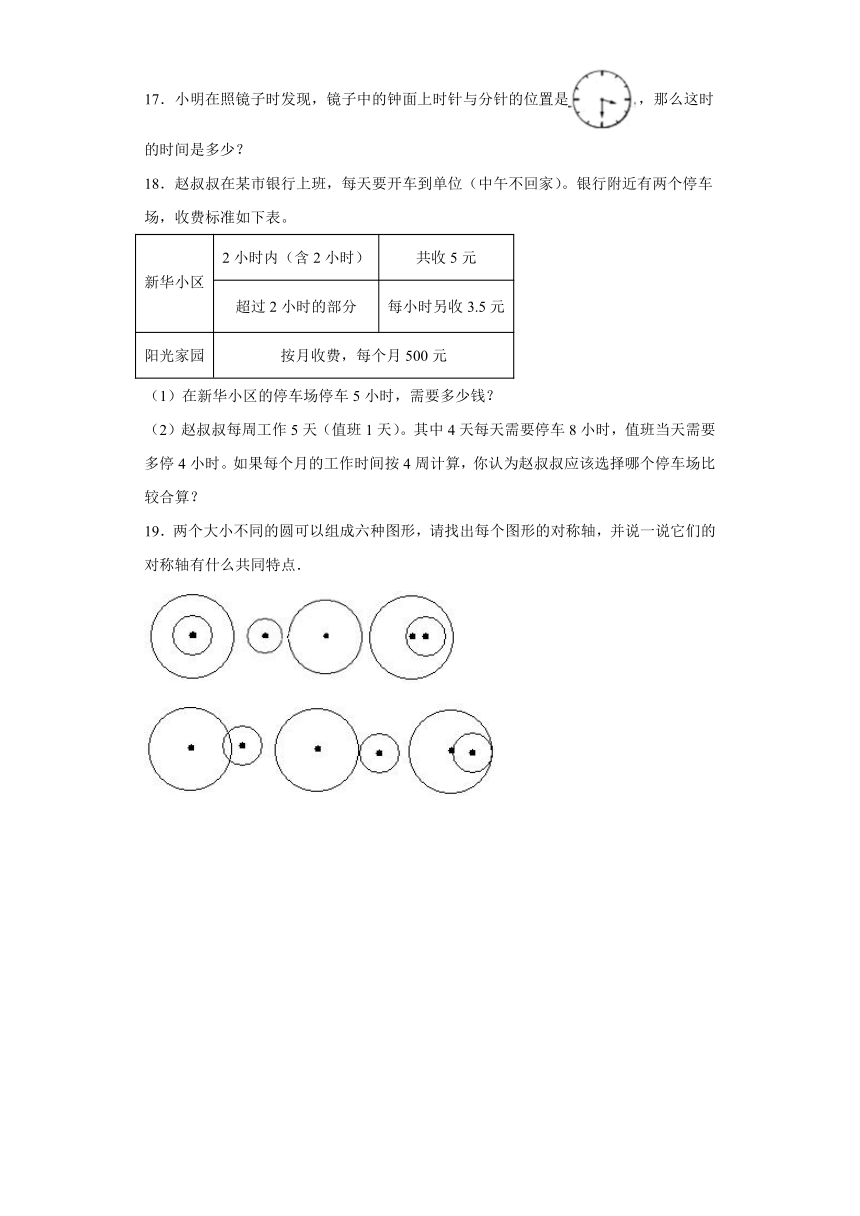
二、填空题
6.在田字格没有棋子的交叉点上再放一颗棋子,这颗棋子要与图上已有的棋子组成轴对称图形,一共有( )种不同的放法。
7.轴对称图形的特点是沿( )对折,两边的部分能够( )。
8.下图中只有两条对称轴的图形有( )和( )。
9.长方形有( )条对称轴,等腰三角形有( )条对称轴,正方形有( ) 条对称轴。
10.请将下列图形对称轴的条数填在下面的括号里。
( )条 ( )条 ( )条 ( )条 ( )条 ( )条
三、判断题
11.轴对称图形的两个对称点到对称轴的距离相等。( )
12.长方形、正方形、圆,等边三角形都是轴对称图形,正方形的对称轴最多。( )
13.,左图有2条对称轴。( )
14.左图只有一条对称轴。( )
15.三角形一定有3条对称轴。( )
四、作图题
16.画出如图所示图形的所有对称轴。
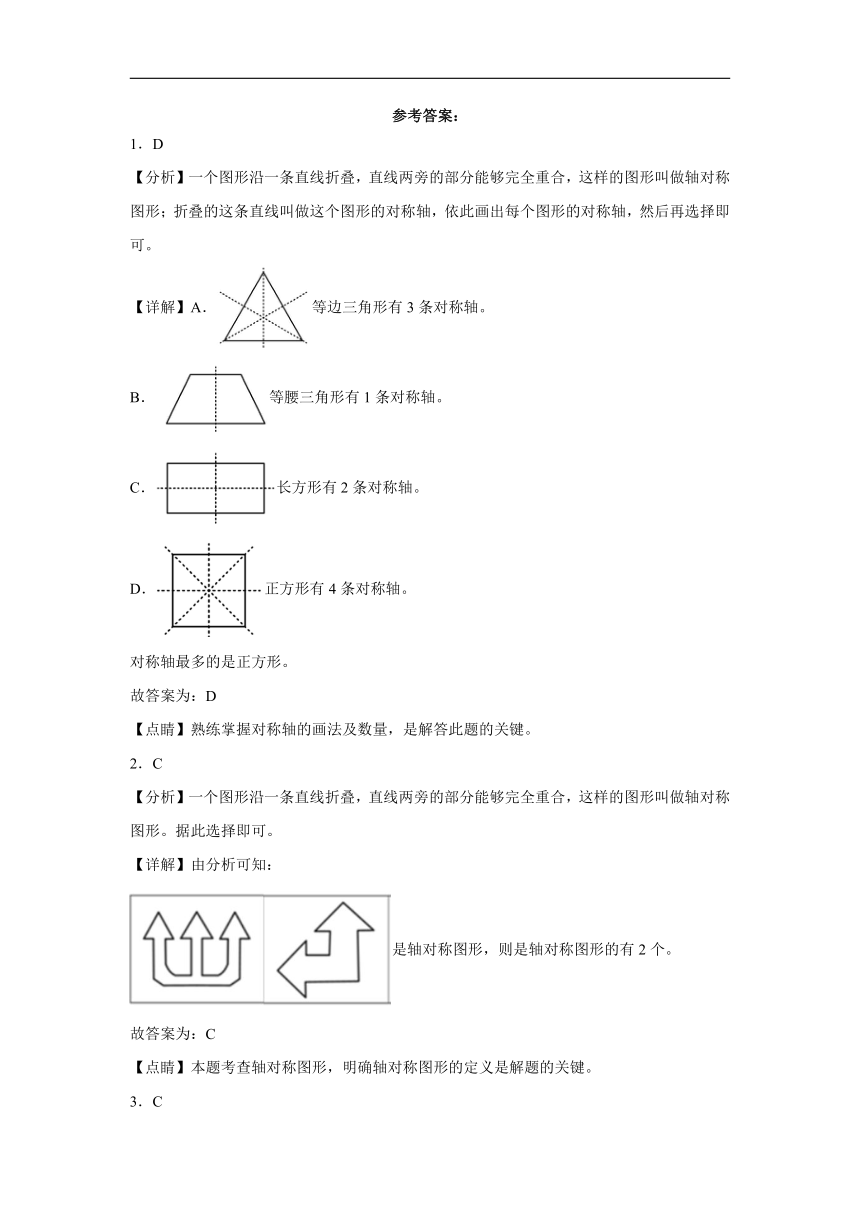
五、解答题
17.小明在照镜子时发现,镜子中的钟面上时针与分针的位置是,那么这时的时间是多少?
18.赵叔叔在某市银行上班,每天要开车到单位(中午不回家)。银行附近有两个停车场,收费标准如下表。
新华小区 2小时内(含2小时) 共收5元
超过2小时的部分 每小时另收3.5元
阳光家园 按月收费,每个月500元
(1)在新华小区的停车场停车5小时,需要多少钱?
(2)赵叔叔每周工作5天(值班1天)。其中4天每天需要停车8小时,值班当天需要多停4小时。如果每个月的工作时间按4周计算,你认为赵叔叔应该选择哪个停车场比较合算?
19.两个大小不同的圆可以组成六种图形,请找出每个图形的对称轴,并说一说它们的对称轴有什么共同特点.
参考答案:
1.D
【分析】一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形;折叠的这条直线叫做这个图形的对称轴,依此画出每个图形的对称轴,然后再选择即可。
【详解】A.等边三角形有3条对称轴。
B. 等腰三角形有1条对称轴。
C.长方形有2条对称轴。
D.正方形有4条对称轴。
对称轴最多的是正方形。
故答案为:D
【点睛】熟练掌握对称轴的画法及数量,是解答此题的关键。
2.C
【分析】一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形。据此选择即可。
【详解】由分析可知:
是轴对称图形,则是轴对称图形的有2个。
故答案为:C
【点睛】本题考查轴对称图形,明确轴对称图形的定义是解题的关键。
3.C
【分析】根据将一张正方形的纸片按如图所示的方式三次折叠,折叠后再按图所示沿折痕MN裁剪,可以动手折叠,再进行裁剪,即可得出答案。
【详解】严格按照图中的顺序向右上对折,向左上角对折,过直角顶点向对边引垂线,沿垂线剪开,展开后可得到四个相同的正方形。
故答案为:C
【点睛】本题主要考查学生的动手能力及空间想象能力。对于此类问题,学生只要亲自动手操作,答案就会很直观地呈现。
4.C
【分析】根据轴对称图形的定义:一个图形沿一条直线对折,直线两旁的部分能够完全重合,则这个图形就是轴对称图形,这条直线就是这个图形的一条对称轴,据此即可解答。
【详解】根据轴对称图形的定义可得:、和是轴对称图形,不是轴对称图形。
故答案为:C
【点睛】明确轴对称图形的定义,是解答此题的关键。
5.D
【分析】此题考查镜面对称,根据镜面对称的性质,在平面镜中的钟面上的时针、分针的位置和实物应关于过12时、6时的直线成轴对称。
【详解】8点的时钟,在镜子里看起来应该是4点,所以最接近8点的时间在镜子里看起来就更接近4点,所以应该是图D所示,最接近8点时间。
故答案为:D
【点睛】考查了镜面对称,这是一道开放性试题,解决此类题注意技巧;注意镜面反射的原理与性质。
6.4
【分析】如果将一个图形沿着一条直线对折,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴。
【详解】根据轴对称的意义可知:如图,、、、一共有4种不同的放法。
【点睛】轴对称图形被对称轴分成的两部分沿对称轴对折后能够完全重合。
7. 对称轴 完全重合
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;由此解答即可。
【详解】由分析可得:
轴对称图形的特点是沿对称轴对折,两边的部分能够完全重合。
【点睛】本题考查了轴对称图形的概念,需要熟练掌握,并且能准确的分辨。
8. ② ③
【分析】在平面内,如果一个图形沿一条直线对折,直线两旁的部分能够完全重合,这个图形就是轴对称图形,这条直线就是它的对称轴,由此即可判断这几个选项中组合图形的对称轴的条数及位置。
【详解】根据轴对称图形的定义可知:
①正方形,有4条对称轴;
②长方形,有2条对称轴;
③椭圆形,有2条对称轴;
④平行四边形不是轴对称图形,对称轴的条数是0条;
⑤等腰三角形,有1条对称轴;
下图中只有两条对称轴的图形有②和③。
【点睛】此题考查了利用轴对称图形的定义判断轴对称图形的对称轴的条数及位置的方法。
9. 2 1 4
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴。长方形有2条对称轴,等腰三角形有1条对称轴,正方形有3条对称轴,据此解答。
【详解】长方形有2条对称轴,等腰三角形有1条对称轴,正方形有4条对称轴。
【点睛】此题考查轴对称图形对称轴的求法,注意等腰三角形与等边三角形的对称轴数量的区别,等边三角形是3条对称轴,等腰三角形是1条对称轴。
10. 4 2 1 1 0 无数
【分析】如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;据此解答。
【详解】根据对称轴的定义可知:正方形有4条对称轴;
长方形有2条对称轴;
等腰三角形有1条对称轴;
等腰梯形有1条对称轴;
平行四边形没有对称轴;
圆有无数条对称轴。
【点睛】本题主要考查对称轴的数量,理解对称轴的意义是解题的关键。
11.√
【分析】轴对称图形是指一个图形沿一条直线折叠后直线两旁的部分能够完全重合,这条直线就是这个轴对称图形的对称轴,轴对称图形中,对称点到对称轴的距离相等。
【详解】在轴对称图形中,轴对称图形的两个对称点到对称轴的距离相等。
原题干说法正确。
故答案为:√
【点睛】掌握轴对称图形的意义及其特点是解答本题的关键。
12.×
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴,据此解答。
【详解】长方形有2条对称轴;
正方形有4条对称轴;
圆有无数条对称轴;
等边三角形有3条对称轴。
长方形、正方形、圆,等边三角形都是轴对称图形,圆的对称轴最多。
原题干说法错误。
故答案为:×
【点睛】熟记常见图形轴对称的条数是解答本题的关键。
13.×
【分析】如果一个平面图形沿着一条直线对折后,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形,这条直线就是这个图形的一条对称轴,由此分析图的对称轴条数,即可解答。
【详解】如图所示:
,有1条对称轴。原题说法错误。
故答案为:×
【点睛】此题主要考查轴对称图形的对称轴数量,掌握对称轴的定义是解题关键。
14.×
【分析】如果一个平面图形沿着一条直线对折后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线就是这个图形的一条对称轴,由此分析图的对称轴条数,即可解答。
【详解】由分析得:
有5条对称轴,如下图所示:
原题干说法错误。
故答案为:×
【点睛】此题主要考查轴对称图形的对称轴数量,掌握对称轴的定义是解题关键。
15.×
【分析】根据轴对称图形的定义,此题应分情况分析:一般三角形不是轴对称图形,没有对称轴;等腰三角形是轴对称图形,只有1条对称轴;等边三角形是轴对称图形,有3条对称轴。
【详解】由分析得:
等边三角形一定有3条对称轴。原题说法错误。
故答案为:×。
【点睛】本题考查轴对称图形的定义,注意本题应按照一般三角形、等腰三角形和等边三角形的情况分析解答。
16.见详解
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;据此画出对称轴。
【详解】
【点睛】此题主要考查轴对称图形的定义及对称轴的条数和画法。
17.8:30
【分析】从镜子中看到的时刻与真实的时刻是相反的,据此解答即可。
【详解】根据镜面对称的性质可知:小明在照镜子时发现,镜子中的钟面上时针与分针的位置是,那么这时的时间是8:30。
【点睛】掌握镜面的对称性是解题的关键。
18.(1)15.5元;(2)阳光家园停车场
【分析】(1)由题意可知,停车5小时分两个时间段收费,2小时内收费5元,超过2小时的部分即5-2=3小时,按每小时3.5元收费。
(2)由题意可知,要选择合算的停车场,需要求出在新华小区停车场的费用,然后与阳光家园停车场费用进行比较。赵叔叔4天每天需要停车8小时,每天停车费用是分两个时间段计算(2小时内和超过2小时),值班当天停12小时也分两个时间段计算(2小时内和超过2小时),然后算出一周的停车费用,接着算出一个月的停车费用,最后通过比较,得出赵叔叔应该选择阳光家园停车场比较合算。
【详解】(1)(5-2)×3.5+5
=3×3.5+5
=15.5(元)
答:需要15.5元。
(2)(8-2)×3.5+5
=6×3.5+5
=21+5
=26(元)
(8+4-2)×3.5+5
=10×3.5+5
=40(元)
(26×4+40)×4
=144×4
=576(元)
576元>500元
答:赵叔叔应该选择阳光家园停车场比较合算。
【点睛】找准数量关系,掌握小数四则混合运算的方法是解题的关键。
19.如图所示
(无数条)
共同点:大小不相同的两个圆所组成的图形,若圆心重合,则有无数条对称轴;若圆心不重合,则只有一条对称轴,这条对称轴是两个圆心相连所在的直线.
【分析】如果一个图形沿一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形,折痕所在的这条直线叫做对称轴.
【详解】如图所示
(无数条)
共同点:大小不相同的两个圆所组成的图形,若圆心重合,则有无数条对称轴;若圆心不重合,则只有一条对称轴,这条对称轴是两个圆心相连所在的直线.
学校:___________姓名:___________班级:___________
一、选择题
1.下面图形中,对称轴最多的是( )。
A.等边三角形 B.等腰梯形 C.长方形 D.正方形
2.下面的图案中,是轴对称图形的有( )个。
A.4 B.3 C.2 D.1
3.将一张正方形纸按下图所示的方式两次折叠,折叠后再按图所示沿MN剪开,则可得( )。
A.多个等腰直角三角形 B.一个等腰直角三角形和一个正方形
C.四个相同的正方形 D.两个相同的正方形
4.如图所示的标志中不是轴对称图形的是( )。
A. B. C. D.
5.下图是小明在镜子中看见身后墙上的钟,时间最接近8时的是( )。
A. B. C. D.
二、填空题
6.在田字格没有棋子的交叉点上再放一颗棋子,这颗棋子要与图上已有的棋子组成轴对称图形,一共有( )种不同的放法。
7.轴对称图形的特点是沿( )对折,两边的部分能够( )。
8.下图中只有两条对称轴的图形有( )和( )。
9.长方形有( )条对称轴,等腰三角形有( )条对称轴,正方形有( ) 条对称轴。
10.请将下列图形对称轴的条数填在下面的括号里。
( )条 ( )条 ( )条 ( )条 ( )条 ( )条
三、判断题
11.轴对称图形的两个对称点到对称轴的距离相等。( )
12.长方形、正方形、圆,等边三角形都是轴对称图形,正方形的对称轴最多。( )
13.,左图有2条对称轴。( )
14.左图只有一条对称轴。( )
15.三角形一定有3条对称轴。( )
四、作图题
16.画出如图所示图形的所有对称轴。
五、解答题
17.小明在照镜子时发现,镜子中的钟面上时针与分针的位置是,那么这时的时间是多少?
18.赵叔叔在某市银行上班,每天要开车到单位(中午不回家)。银行附近有两个停车场,收费标准如下表。
新华小区 2小时内(含2小时) 共收5元
超过2小时的部分 每小时另收3.5元
阳光家园 按月收费,每个月500元
(1)在新华小区的停车场停车5小时,需要多少钱?
(2)赵叔叔每周工作5天(值班1天)。其中4天每天需要停车8小时,值班当天需要多停4小时。如果每个月的工作时间按4周计算,你认为赵叔叔应该选择哪个停车场比较合算?
19.两个大小不同的圆可以组成六种图形,请找出每个图形的对称轴,并说一说它们的对称轴有什么共同特点.
参考答案:
1.D
【分析】一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形;折叠的这条直线叫做这个图形的对称轴,依此画出每个图形的对称轴,然后再选择即可。
【详解】A.等边三角形有3条对称轴。
B. 等腰三角形有1条对称轴。
C.长方形有2条对称轴。
D.正方形有4条对称轴。
对称轴最多的是正方形。
故答案为:D
【点睛】熟练掌握对称轴的画法及数量,是解答此题的关键。
2.C
【分析】一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形。据此选择即可。
【详解】由分析可知:
是轴对称图形,则是轴对称图形的有2个。
故答案为:C
【点睛】本题考查轴对称图形,明确轴对称图形的定义是解题的关键。
3.C
【分析】根据将一张正方形的纸片按如图所示的方式三次折叠,折叠后再按图所示沿折痕MN裁剪,可以动手折叠,再进行裁剪,即可得出答案。
【详解】严格按照图中的顺序向右上对折,向左上角对折,过直角顶点向对边引垂线,沿垂线剪开,展开后可得到四个相同的正方形。
故答案为:C
【点睛】本题主要考查学生的动手能力及空间想象能力。对于此类问题,学生只要亲自动手操作,答案就会很直观地呈现。
4.C
【分析】根据轴对称图形的定义:一个图形沿一条直线对折,直线两旁的部分能够完全重合,则这个图形就是轴对称图形,这条直线就是这个图形的一条对称轴,据此即可解答。
【详解】根据轴对称图形的定义可得:、和是轴对称图形,不是轴对称图形。
故答案为:C
【点睛】明确轴对称图形的定义,是解答此题的关键。
5.D
【分析】此题考查镜面对称,根据镜面对称的性质,在平面镜中的钟面上的时针、分针的位置和实物应关于过12时、6时的直线成轴对称。
【详解】8点的时钟,在镜子里看起来应该是4点,所以最接近8点的时间在镜子里看起来就更接近4点,所以应该是图D所示,最接近8点时间。
故答案为:D
【点睛】考查了镜面对称,这是一道开放性试题,解决此类题注意技巧;注意镜面反射的原理与性质。
6.4
【分析】如果将一个图形沿着一条直线对折,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴。
【详解】根据轴对称的意义可知:如图,、、、一共有4种不同的放法。
【点睛】轴对称图形被对称轴分成的两部分沿对称轴对折后能够完全重合。
7. 对称轴 完全重合
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;由此解答即可。
【详解】由分析可得:
轴对称图形的特点是沿对称轴对折,两边的部分能够完全重合。
【点睛】本题考查了轴对称图形的概念,需要熟练掌握,并且能准确的分辨。
8. ② ③
【分析】在平面内,如果一个图形沿一条直线对折,直线两旁的部分能够完全重合,这个图形就是轴对称图形,这条直线就是它的对称轴,由此即可判断这几个选项中组合图形的对称轴的条数及位置。
【详解】根据轴对称图形的定义可知:
①正方形,有4条对称轴;
②长方形,有2条对称轴;
③椭圆形,有2条对称轴;
④平行四边形不是轴对称图形,对称轴的条数是0条;
⑤等腰三角形,有1条对称轴;
下图中只有两条对称轴的图形有②和③。
【点睛】此题考查了利用轴对称图形的定义判断轴对称图形的对称轴的条数及位置的方法。
9. 2 1 4
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴。长方形有2条对称轴,等腰三角形有1条对称轴,正方形有3条对称轴,据此解答。
【详解】长方形有2条对称轴,等腰三角形有1条对称轴,正方形有4条对称轴。
【点睛】此题考查轴对称图形对称轴的求法,注意等腰三角形与等边三角形的对称轴数量的区别,等边三角形是3条对称轴,等腰三角形是1条对称轴。
10. 4 2 1 1 0 无数
【分析】如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;据此解答。
【详解】根据对称轴的定义可知:正方形有4条对称轴;
长方形有2条对称轴;
等腰三角形有1条对称轴;
等腰梯形有1条对称轴;
平行四边形没有对称轴;
圆有无数条对称轴。
【点睛】本题主要考查对称轴的数量,理解对称轴的意义是解题的关键。
11.√
【分析】轴对称图形是指一个图形沿一条直线折叠后直线两旁的部分能够完全重合,这条直线就是这个轴对称图形的对称轴,轴对称图形中,对称点到对称轴的距离相等。
【详解】在轴对称图形中,轴对称图形的两个对称点到对称轴的距离相等。
原题干说法正确。
故答案为:√
【点睛】掌握轴对称图形的意义及其特点是解答本题的关键。
12.×
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴,据此解答。
【详解】长方形有2条对称轴;
正方形有4条对称轴;
圆有无数条对称轴;
等边三角形有3条对称轴。
长方形、正方形、圆,等边三角形都是轴对称图形,圆的对称轴最多。
原题干说法错误。
故答案为:×
【点睛】熟记常见图形轴对称的条数是解答本题的关键。
13.×
【分析】如果一个平面图形沿着一条直线对折后,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形,这条直线就是这个图形的一条对称轴,由此分析图的对称轴条数,即可解答。
【详解】如图所示:
,有1条对称轴。原题说法错误。
故答案为:×
【点睛】此题主要考查轴对称图形的对称轴数量,掌握对称轴的定义是解题关键。
14.×
【分析】如果一个平面图形沿着一条直线对折后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线就是这个图形的一条对称轴,由此分析图的对称轴条数,即可解答。
【详解】由分析得:
有5条对称轴,如下图所示:
原题干说法错误。
故答案为:×
【点睛】此题主要考查轴对称图形的对称轴数量,掌握对称轴的定义是解题关键。
15.×
【分析】根据轴对称图形的定义,此题应分情况分析:一般三角形不是轴对称图形,没有对称轴;等腰三角形是轴对称图形,只有1条对称轴;等边三角形是轴对称图形,有3条对称轴。
【详解】由分析得:
等边三角形一定有3条对称轴。原题说法错误。
故答案为:×。
【点睛】本题考查轴对称图形的定义,注意本题应按照一般三角形、等腰三角形和等边三角形的情况分析解答。
16.见详解
【分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;据此画出对称轴。
【详解】
【点睛】此题主要考查轴对称图形的定义及对称轴的条数和画法。
17.8:30
【分析】从镜子中看到的时刻与真实的时刻是相反的,据此解答即可。
【详解】根据镜面对称的性质可知:小明在照镜子时发现,镜子中的钟面上时针与分针的位置是,那么这时的时间是8:30。
【点睛】掌握镜面的对称性是解题的关键。
18.(1)15.5元;(2)阳光家园停车场
【分析】(1)由题意可知,停车5小时分两个时间段收费,2小时内收费5元,超过2小时的部分即5-2=3小时,按每小时3.5元收费。
(2)由题意可知,要选择合算的停车场,需要求出在新华小区停车场的费用,然后与阳光家园停车场费用进行比较。赵叔叔4天每天需要停车8小时,每天停车费用是分两个时间段计算(2小时内和超过2小时),值班当天停12小时也分两个时间段计算(2小时内和超过2小时),然后算出一周的停车费用,接着算出一个月的停车费用,最后通过比较,得出赵叔叔应该选择阳光家园停车场比较合算。
【详解】(1)(5-2)×3.5+5
=3×3.5+5
=15.5(元)
答:需要15.5元。
(2)(8-2)×3.5+5
=6×3.5+5
=21+5
=26(元)
(8+4-2)×3.5+5
=10×3.5+5
=40(元)
(26×4+40)×4
=144×4
=576(元)
576元>500元
答:赵叔叔应该选择阳光家园停车场比较合算。
【点睛】找准数量关系,掌握小数四则混合运算的方法是解题的关键。
19.如图所示
(无数条)
共同点:大小不相同的两个圆所组成的图形,若圆心重合,则有无数条对称轴;若圆心不重合,则只有一条对称轴,这条对称轴是两个圆心相连所在的直线.
【分析】如果一个图形沿一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形,折痕所在的这条直线叫做对称轴.
【详解】如图所示
(无数条)
共同点:大小不相同的两个圆所组成的图形,若圆心重合,则有无数条对称轴;若圆心不重合,则只有一条对称轴,这条对称轴是两个圆心相连所在的直线.
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
