五四制鲁教版七年级上册期末测试数学卷(含答案)
文档属性
| 名称 | 五四制鲁教版七年级上册期末测试数学卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 7.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-25 21:55:55 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
五四制鲁教版数学七年级上册期末测试卷
(时间:120分钟 分值:150分)
一、选择题(每小题4分,共 40分)
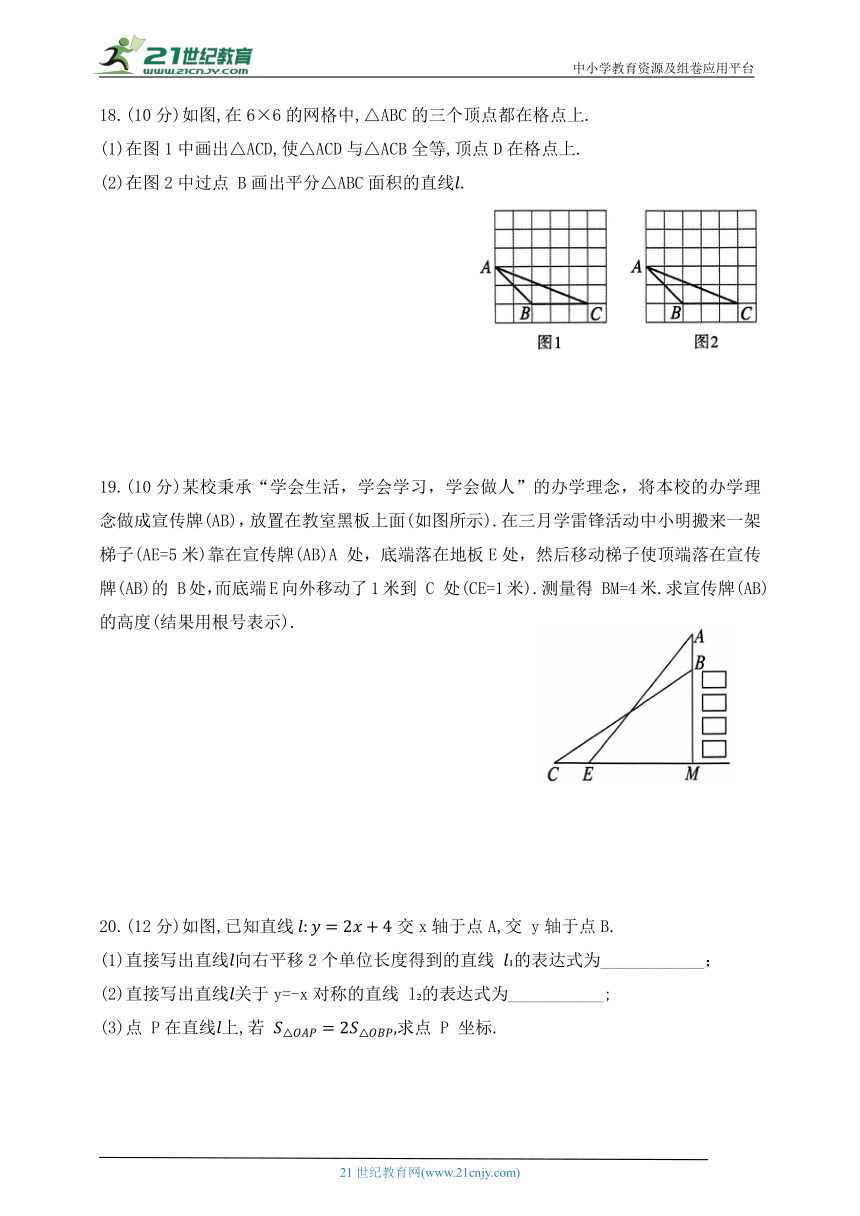
1.下列图形:
其中轴对称图形的个数是( )
A.4 B.3 C.2 D.1
2.下列实数中是无理数的是( )
A.
3.若点 A(-4,m-3),B(2n,1)关于x轴对称,则( )
A. m=2,n=0 B. m=2,n=-2 C. m=4,n=2 D. m=4,n=-2
4.如图,在△ABC 和△DEF 中,点 A,E,B,D在同一直线上,AC∥DF,AC=DF,只添加一个条件,能判定△ABC≌△DEF的是( )
A. BC=DE B. AE=DB C.∠A=∠DEF D.∠ABC=∠D
5.若ab<0且a>b,则函数 y=ax+b的图象可能是( )
6.如图,数轴上点 M所表示的数为m,则m的值是( )
7.已知 a,b,c是△ABC的三边长,如果那么 △ABC是( )
A.以a为斜边的直角三角形 B.以b为斜边的直角三角形
C.以c为斜边的直角三角形 D.不是直角三角形
8.如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段 AB 上任意一点(不包括端点),过点 P 分别作两坐标轴的垂线与两坐标轴围成的长方形的周长为8,则该直线的函数表达式是( )
第8题图 第9题图
9.如图,△ABC中,AB,AC的垂直平分线l ,l 相交于点O,若∠BAC=76°,则∠OBC=( )
A.14° B.76° C.28° D.38°
10.如图,一次函数 y=x+4的图象与 x轴,y轴分别交于点A,B,点C(-2,0)是 x轴上一点,点 E,F分别为直线 y=x+4和y轴上的两个动点,当△CEF周长最小时,点 E,F的坐标分别为( )
F(0,2)
B. E(-2,2),F(0,2)
二、填空题(每小题 5分,共30分)
的平方根是_____________.
12.如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别是A(-2,1)和 B(-2,-3),那么第一架轰炸机C的平面坐标是____________.
第12题图 第13题图
13.如图,与图中直线 y=-x+1关于x轴对称的直线的函数表达式是___________.
14.如图,在 Rt△ABC中,∠C=90°,AC=3,AB=5,以点 A为圆心,以任意长为半径作弧,分别交 AB,AC 于点M,N,再分别以M,N为圆心,以大于 的长为半径作弧,两弧交于点 P,作射线 AP 交 BC 于点 D,则 CD 的长是_____________.
第14题图 第15题图
15.如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且 DC=BC,AD=AO,若∠BAC=80°,则∠BCA 的度数为____________.
16.甲、乙两人沿同一条直路跑步,如果两人分别从这条路上的A,B两处同时出发,都以不变的速度相向而行,图1是甲离开A处后行走的路程y(单位:m)与行走时间x(单位:min)的函数图象,图2是甲、乙两人之间的距离(单位:m)与甲行走时间x(单位:min)的函数图象,则a-b=___________.
三、解答题(本大题共 7 小题,共 80分)
17.(10分)(1)计算:
(2)计算:
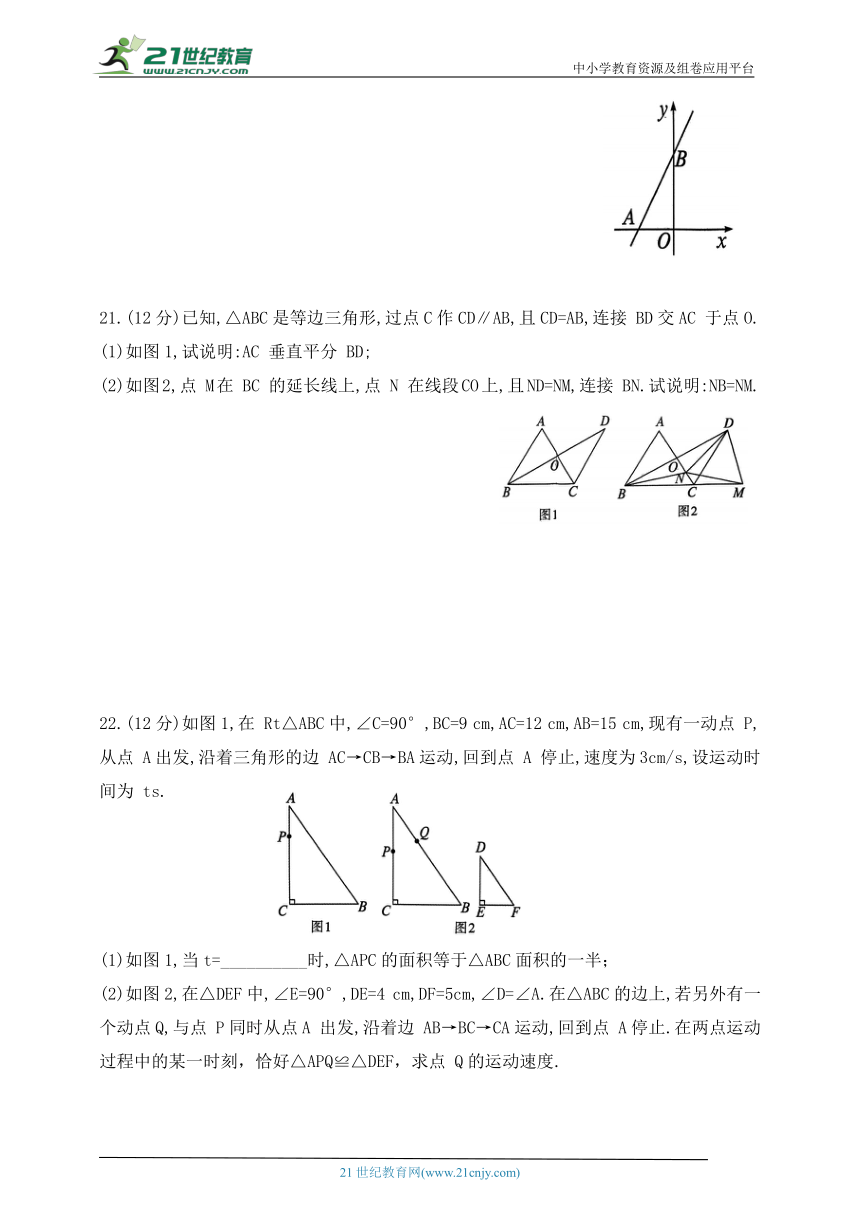
18.(10分)如图,在6×6的网格中,△ABC的三个顶点都在格点上.
(1)在图1中画出△ACD,使△ACD与△ACB全等,顶点D在格点上.
(2)在图2中过点 B画出平分△ABC面积的直线.
19.(10分)某校秉承“学会生活,学会学习,学会做人”的办学理念,将本校的办学理念做成宣传牌(AB),放置在教室黑板上面(如图所示).在三月学雷锋活动中小明搬来一架
梯子(AE=5米)靠在宣传牌(AB)A 处,底端落在地板E处,然后移动梯子使顶端落在宣传牌(AB)的 B处,而底端E向外移动了1米到 C 处(CE=1米).测量得 BM=4米.求宣传牌(AB)的高度(结果用根号表示).
20.(12分)如图,已知直线交x轴于点A,交 y轴于点B.
(1)直接写出直线向右平移2个单位长度得到的直线 的表达式为____________;
(2)直接写出直线关于y=-x对称的直线 l 的表达式为___________;
(3)点 P在直线上,若 求点 P 坐标.
21.(12分)已知,△ABC是等边三角形,过点C作CD∥AB,且CD=AB,连接 BD交AC 于点O.
(1)如图1,试说明:AC 垂直平分 BD;
(2)如图2,点 M在 BC 的延长线上,点 N 在线段CO上,且ND=NM,连接 BN.试说明:NB=NM.
22.(12分)如图1,在 Rt△ABC中,∠C=90°,BC=9 cm,AC=12 cm,AB=15 cm,现有一动点 P,从点 A出发,沿着三角形的边 AC→CB→BA运动,回到点 A 停止,速度为3cm/s,设运动时间为 ts.
(1)如图1,当t=__________时,△APC的面积等于△ABC面积的一半;
(2)如图2,在△DEF中,∠E=90°,DE=4 cm,DF=5cm,∠D=∠A.在△ABC的边上,若另外有一个动点Q,与点 P同时从点A 出发,沿着边 AB→BC→CA运动,回到点 A停止.在两点运动过程中的某一时刻,恰好△APQ≌△DEF,求点 Q的运动速度.
23.(14分)“五·一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.
根据以上信息,解答下列问题:
(1)设租车时间为 x小时,租用甲公司的车所需费用为 y 元,租用乙公司的车所需费用为 y 元,分别求出 y ,y 关于x的函数表达式;
(2)请你帮助小明计算选择哪个出游方式合算.
参考答案
一、选择题
1. B
2. D【解析】A项, 是分数,是有理数;B项,由于 所以 是整数,是有理数;C项, 是无限循环小数,是有理数;D项,由于 中分子是 是开方开不尽的方根,所以 是无理数.故选D.
3. B 【解析】关于x轴对称的两个点的纵坐标互为相反数,横坐标相等,所以m-3=-1,2n=-4,所以m=2,n=-2.故选B.
4. B【解析】因为AC∥DF,所以∠A=∠D.因为AC=DF,所以当添加AE=DB时,可得AB=DE,可根据“SAS”判定△ABC≌△DEF.故选B.
5. A【解析】因为 ab<0,且a>b,所以a>0,b<0.所以函数y=ax+b的图象经过第一、三、四象限.故选A.
6. B【解析】直角三角形的斜边长 所以点 M表示的数为 故选 B.
7. A【解析】因为a -26a+169=(a-13) ,所以
所以a=13,b=12,c=5.因为5 +12 =25+144=169=13 ,所以以a,b,c为三边的三角形是以a为斜边的直角三角形.故选A.
8. A 【解析】设点P坐标为(x,y).因为点P在第一象限,所以PC=x,PD=y.因为长方形 PDOC的周长为8;所以2(x+y)=8,x+y=4.所以该直线的函数表达式是 y=-x+4.故选 A.
9. A 【解析】连接OA.因为 AB,AC的垂直平分线 , 相交于点O,所以OA=OB,OA=OC.所以∠OBA=∠OAB,∠OCA=∠OAC,OB=OC.所以∠OBA+∠OCA=∠BAC=76°.所以∠OBC+ ∠OCB=180°-∠BAC-(∠OBA+∠OCA)=28°.因为OB=OC,所以∠OBC=∠OCB=14°.
故答案为 14°.故选A.
10. C【解析】作C(-2,0)关于y轴的对称点G(2,0),作C(-2,0)关于直线 y=x+4的对称点D,连接AD,连接DG交AB于点E,交y轴于点F,如图.
所以DE=CE,CF=GF,所以CE+CF+EF=DE+GF+EF=DG,此时△CEF 周长最小.
由y=x+4,得A的坐标为(-4,0),B的坐标为(0,4).所以OA = OB,△AOB 是等腰直角三角形.所以∠BAC=45°.
因为点C,D关于AB对称,所以∠DAB=∠BAC=45°.所以∠DAC=90°.因为C的坐标为(-2,0).所以AC=OA-OC=2=AD.所以点D的坐标为(-4,2).
由D(-4,2),G(2,0)可得直线 DG的表达式为
在 中,令x=0,得 所以点F的坐标为
由 得所以点E的坐标为
所以点E的坐标为 点F的坐标为 故选C.
二、填空题
12.(2,-1)【解析】由A,B两点的坐标知:每个单元格的边长恰为平面直角坐标系中的单位长度,网格线为坐标轴所在直线,原点在A点右边两个单位长度、下方一个单位长度的位置上.由此可建立平面直角坐标系,如图所示.显然C点的坐标为(2,-1).故答案为(2,-1).
13. y=x-1 【解析】因为关于x轴对称的点横坐标相等,纵坐标互为相反数,所以直线 y=-x+1关于x轴对称的直线的函数表达式是-y=-x+1,即y=x-1.故答案为y=x-1.
【解析】如图,作DH⊥AB于点H.由作图可知AD平分∠BAC,所以∠DAH=∠DAC.
因为∠AHD=∠C=90°,AD=AD,所以△ADH≌△ADC(AAS).所以DH=DC,AH=AC=3.
在Rt△ABC中,因为AB=5,AC=3,所以 设DC=DH=m,
在Rt△BHD中,因为BD =BH +DH ,所以(4-m) =2 +m ,
所以 所以
15.60°【解析】因为△ABC三个内角的平分线交于点O,所以∠ACO=∠BCO.在△COD 和△COB中,CD=CB,∠ACO=∠BCO,OC=OC,所以△COD≌△COB(SAS),所以∠D=∠CBO.因为∠BAC=80°,所以∠BAD=100°,∠BAO=40°.所以∠DAO=140°.因为AD=AO,所以∠D=20°.所以∠CBO=20°,所以∠ABC=40°,所以∠BCA=60°.故答案为60°.
16. 【解析】从图1可得甲的速度为
从图2可以看出,当 时,二人相遇,即(60+v )×解得
因为乙的速度快,从图2看出乙用了b分钟走完全程,甲用了a分钟走完全程, 故答案为
三、解答题
17.解: 4×9+(-6)÷(-2)=-1+36+3=38.
18.解:(1)如图1中,△ADC 即为所求.
(2)如图2中,直线 BT 即为所求.
19.解:由题意可得 AE=BC=5米,BM=4米,EC=1米.
在 Rt△MBC中, (米).则 EM=3-1=2(米).
在Rt△AEM中, (米),故 米.
答:宣传牌(AB)的高度为( 米.
20.解:(1)y=2x
【解析】因为(0,4),(-2,0)在直线:y=2x+4上,这两点关于y=-x的对称点为(-4,0),(0,2).设直线 的表达式为 y=kx+b(k≠0),
所以 解得 所以直线 的表达式为
故答案为
(3)因为直线l:y=2x+4交x轴于点A,交y轴于点B,所以A的坐标为(-2,0),B的坐标为(0,4).所以OA=2,OB=4.
设点 P的坐标为(x,2x+4),
因为 所以 |x|,即|2x+4|=4|x|.
解得 或2.当 时, 当x=2时,y=2x+4=8,
所以点 P的坐标为 或(2,8).
21.解:(1)因为△ABC是等边三角形,所以∠ABC=∠ACB=∠CAB=60°,AB=AC=BC.
因为 CD=AB,所以CD=CA=BC.
因为CD∥AB,所以∠ACD=∠BAC=60°.所以∠ACD=∠BCA=60°.
所以 BO=DO,CO⊥BD,即AC垂直平分 BD.
(2)由(1)知AC垂直平分 BD,所以NB=ND.因为 ND=NM,所以 NB=NM.
22.解: 或 【解析】①当点P在BC上时,如图1,
若△APC的面积等于△ABC面积的一半,则 CP=此时,点P移动的距离为AC+CP=12+ 移动的时间为 (秒).
②当点P在BA上时,如图2,
若△APC的面积等于△ABC面积的一半,则点 P为BA的中点,
此时,点 P移动的距离为AC+CB+BP=12+9+
移动的时间为 (秒).
故答案为 或
(2)△APQ≌△DEF,对应顶点为 A与D,P与E,Q与F.
①当点 P在AC上,如图3所示.
此时AP=4,AQ=5,所以点Q移动的速度为5÷(4÷3)
②当点 P在AB上,如图4所示.此时,AP=4,AQ=5,
点 P移动的距离为9+12+15-4=32(cm),点 Q移动的距离为9+12+15-5=31(cm),
所以点Q移动的速度为 综上所述,两点运动过程中的某一时刻,恰好△APQ≌△DEF,点Q的运动速度为 或
23.解:(1)由题意可设y =k x+80(k ≠0).
图象过点(1,95),则有95=k +80.
所以k =15.所以y =15x+80(x≥0).
由题意,得 y =30x(x≥0).
(2)当y =y 时,15x+80=30x,解得 所以当租车
时间为 小时时,选择甲、乙公司一样合算;
当租车时间小于 小时时,选择乙公司合算;
当租车时间大于 小时时,选择甲公司合算.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
五四制鲁教版数学七年级上册期末测试卷
(时间:120分钟 分值:150分)
一、选择题(每小题4分,共 40分)
1.下列图形:
其中轴对称图形的个数是( )
A.4 B.3 C.2 D.1
2.下列实数中是无理数的是( )
A.
3.若点 A(-4,m-3),B(2n,1)关于x轴对称,则( )
A. m=2,n=0 B. m=2,n=-2 C. m=4,n=2 D. m=4,n=-2
4.如图,在△ABC 和△DEF 中,点 A,E,B,D在同一直线上,AC∥DF,AC=DF,只添加一个条件,能判定△ABC≌△DEF的是( )
A. BC=DE B. AE=DB C.∠A=∠DEF D.∠ABC=∠D
5.若ab<0且a>b,则函数 y=ax+b的图象可能是( )
6.如图,数轴上点 M所表示的数为m,则m的值是( )
7.已知 a,b,c是△ABC的三边长,如果那么 △ABC是( )
A.以a为斜边的直角三角形 B.以b为斜边的直角三角形
C.以c为斜边的直角三角形 D.不是直角三角形
8.如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段 AB 上任意一点(不包括端点),过点 P 分别作两坐标轴的垂线与两坐标轴围成的长方形的周长为8,则该直线的函数表达式是( )
第8题图 第9题图
9.如图,△ABC中,AB,AC的垂直平分线l ,l 相交于点O,若∠BAC=76°,则∠OBC=( )
A.14° B.76° C.28° D.38°
10.如图,一次函数 y=x+4的图象与 x轴,y轴分别交于点A,B,点C(-2,0)是 x轴上一点,点 E,F分别为直线 y=x+4和y轴上的两个动点,当△CEF周长最小时,点 E,F的坐标分别为( )
F(0,2)
B. E(-2,2),F(0,2)
二、填空题(每小题 5分,共30分)
的平方根是_____________.
12.如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别是A(-2,1)和 B(-2,-3),那么第一架轰炸机C的平面坐标是____________.
第12题图 第13题图
13.如图,与图中直线 y=-x+1关于x轴对称的直线的函数表达式是___________.
14.如图,在 Rt△ABC中,∠C=90°,AC=3,AB=5,以点 A为圆心,以任意长为半径作弧,分别交 AB,AC 于点M,N,再分别以M,N为圆心,以大于 的长为半径作弧,两弧交于点 P,作射线 AP 交 BC 于点 D,则 CD 的长是_____________.
第14题图 第15题图
15.如图,已知△ABC三个内角的平分线交于点O,点D在CA的延长线上,且 DC=BC,AD=AO,若∠BAC=80°,则∠BCA 的度数为____________.
16.甲、乙两人沿同一条直路跑步,如果两人分别从这条路上的A,B两处同时出发,都以不变的速度相向而行,图1是甲离开A处后行走的路程y(单位:m)与行走时间x(单位:min)的函数图象,图2是甲、乙两人之间的距离(单位:m)与甲行走时间x(单位:min)的函数图象,则a-b=___________.
三、解答题(本大题共 7 小题,共 80分)
17.(10分)(1)计算:
(2)计算:
18.(10分)如图,在6×6的网格中,△ABC的三个顶点都在格点上.
(1)在图1中画出△ACD,使△ACD与△ACB全等,顶点D在格点上.
(2)在图2中过点 B画出平分△ABC面积的直线.
19.(10分)某校秉承“学会生活,学会学习,学会做人”的办学理念,将本校的办学理念做成宣传牌(AB),放置在教室黑板上面(如图所示).在三月学雷锋活动中小明搬来一架
梯子(AE=5米)靠在宣传牌(AB)A 处,底端落在地板E处,然后移动梯子使顶端落在宣传牌(AB)的 B处,而底端E向外移动了1米到 C 处(CE=1米).测量得 BM=4米.求宣传牌(AB)的高度(结果用根号表示).
20.(12分)如图,已知直线交x轴于点A,交 y轴于点B.
(1)直接写出直线向右平移2个单位长度得到的直线 的表达式为____________;
(2)直接写出直线关于y=-x对称的直线 l 的表达式为___________;
(3)点 P在直线上,若 求点 P 坐标.
21.(12分)已知,△ABC是等边三角形,过点C作CD∥AB,且CD=AB,连接 BD交AC 于点O.
(1)如图1,试说明:AC 垂直平分 BD;
(2)如图2,点 M在 BC 的延长线上,点 N 在线段CO上,且ND=NM,连接 BN.试说明:NB=NM.
22.(12分)如图1,在 Rt△ABC中,∠C=90°,BC=9 cm,AC=12 cm,AB=15 cm,现有一动点 P,从点 A出发,沿着三角形的边 AC→CB→BA运动,回到点 A 停止,速度为3cm/s,设运动时间为 ts.
(1)如图1,当t=__________时,△APC的面积等于△ABC面积的一半;
(2)如图2,在△DEF中,∠E=90°,DE=4 cm,DF=5cm,∠D=∠A.在△ABC的边上,若另外有一个动点Q,与点 P同时从点A 出发,沿着边 AB→BC→CA运动,回到点 A停止.在两点运动过程中的某一时刻,恰好△APQ≌△DEF,求点 Q的运动速度.
23.(14分)“五·一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.
根据以上信息,解答下列问题:
(1)设租车时间为 x小时,租用甲公司的车所需费用为 y 元,租用乙公司的车所需费用为 y 元,分别求出 y ,y 关于x的函数表达式;
(2)请你帮助小明计算选择哪个出游方式合算.
参考答案
一、选择题
1. B
2. D【解析】A项, 是分数,是有理数;B项,由于 所以 是整数,是有理数;C项, 是无限循环小数,是有理数;D项,由于 中分子是 是开方开不尽的方根,所以 是无理数.故选D.
3. B 【解析】关于x轴对称的两个点的纵坐标互为相反数,横坐标相等,所以m-3=-1,2n=-4,所以m=2,n=-2.故选B.
4. B【解析】因为AC∥DF,所以∠A=∠D.因为AC=DF,所以当添加AE=DB时,可得AB=DE,可根据“SAS”判定△ABC≌△DEF.故选B.
5. A【解析】因为 ab<0,且a>b,所以a>0,b<0.所以函数y=ax+b的图象经过第一、三、四象限.故选A.
6. B【解析】直角三角形的斜边长 所以点 M表示的数为 故选 B.
7. A【解析】因为a -26a+169=(a-13) ,所以
所以a=13,b=12,c=5.因为5 +12 =25+144=169=13 ,所以以a,b,c为三边的三角形是以a为斜边的直角三角形.故选A.
8. A 【解析】设点P坐标为(x,y).因为点P在第一象限,所以PC=x,PD=y.因为长方形 PDOC的周长为8;所以2(x+y)=8,x+y=4.所以该直线的函数表达式是 y=-x+4.故选 A.
9. A 【解析】连接OA.因为 AB,AC的垂直平分线 , 相交于点O,所以OA=OB,OA=OC.所以∠OBA=∠OAB,∠OCA=∠OAC,OB=OC.所以∠OBA+∠OCA=∠BAC=76°.所以∠OBC+ ∠OCB=180°-∠BAC-(∠OBA+∠OCA)=28°.因为OB=OC,所以∠OBC=∠OCB=14°.
故答案为 14°.故选A.
10. C【解析】作C(-2,0)关于y轴的对称点G(2,0),作C(-2,0)关于直线 y=x+4的对称点D,连接AD,连接DG交AB于点E,交y轴于点F,如图.
所以DE=CE,CF=GF,所以CE+CF+EF=DE+GF+EF=DG,此时△CEF 周长最小.
由y=x+4,得A的坐标为(-4,0),B的坐标为(0,4).所以OA = OB,△AOB 是等腰直角三角形.所以∠BAC=45°.
因为点C,D关于AB对称,所以∠DAB=∠BAC=45°.所以∠DAC=90°.因为C的坐标为(-2,0).所以AC=OA-OC=2=AD.所以点D的坐标为(-4,2).
由D(-4,2),G(2,0)可得直线 DG的表达式为
在 中,令x=0,得 所以点F的坐标为
由 得所以点E的坐标为
所以点E的坐标为 点F的坐标为 故选C.
二、填空题
12.(2,-1)【解析】由A,B两点的坐标知:每个单元格的边长恰为平面直角坐标系中的单位长度,网格线为坐标轴所在直线,原点在A点右边两个单位长度、下方一个单位长度的位置上.由此可建立平面直角坐标系,如图所示.显然C点的坐标为(2,-1).故答案为(2,-1).
13. y=x-1 【解析】因为关于x轴对称的点横坐标相等,纵坐标互为相反数,所以直线 y=-x+1关于x轴对称的直线的函数表达式是-y=-x+1,即y=x-1.故答案为y=x-1.
【解析】如图,作DH⊥AB于点H.由作图可知AD平分∠BAC,所以∠DAH=∠DAC.
因为∠AHD=∠C=90°,AD=AD,所以△ADH≌△ADC(AAS).所以DH=DC,AH=AC=3.
在Rt△ABC中,因为AB=5,AC=3,所以 设DC=DH=m,
在Rt△BHD中,因为BD =BH +DH ,所以(4-m) =2 +m ,
所以 所以
15.60°【解析】因为△ABC三个内角的平分线交于点O,所以∠ACO=∠BCO.在△COD 和△COB中,CD=CB,∠ACO=∠BCO,OC=OC,所以△COD≌△COB(SAS),所以∠D=∠CBO.因为∠BAC=80°,所以∠BAD=100°,∠BAO=40°.所以∠DAO=140°.因为AD=AO,所以∠D=20°.所以∠CBO=20°,所以∠ABC=40°,所以∠BCA=60°.故答案为60°.
16. 【解析】从图1可得甲的速度为
从图2可以看出,当 时,二人相遇,即(60+v )×解得
因为乙的速度快,从图2看出乙用了b分钟走完全程,甲用了a分钟走完全程, 故答案为
三、解答题
17.解: 4×9+(-6)÷(-2)=-1+36+3=38.
18.解:(1)如图1中,△ADC 即为所求.
(2)如图2中,直线 BT 即为所求.
19.解:由题意可得 AE=BC=5米,BM=4米,EC=1米.
在 Rt△MBC中, (米).则 EM=3-1=2(米).
在Rt△AEM中, (米),故 米.
答:宣传牌(AB)的高度为( 米.
20.解:(1)y=2x
【解析】因为(0,4),(-2,0)在直线:y=2x+4上,这两点关于y=-x的对称点为(-4,0),(0,2).设直线 的表达式为 y=kx+b(k≠0),
所以 解得 所以直线 的表达式为
故答案为
(3)因为直线l:y=2x+4交x轴于点A,交y轴于点B,所以A的坐标为(-2,0),B的坐标为(0,4).所以OA=2,OB=4.
设点 P的坐标为(x,2x+4),
因为 所以 |x|,即|2x+4|=4|x|.
解得 或2.当 时, 当x=2时,y=2x+4=8,
所以点 P的坐标为 或(2,8).
21.解:(1)因为△ABC是等边三角形,所以∠ABC=∠ACB=∠CAB=60°,AB=AC=BC.
因为 CD=AB,所以CD=CA=BC.
因为CD∥AB,所以∠ACD=∠BAC=60°.所以∠ACD=∠BCA=60°.
所以 BO=DO,CO⊥BD,即AC垂直平分 BD.
(2)由(1)知AC垂直平分 BD,所以NB=ND.因为 ND=NM,所以 NB=NM.
22.解: 或 【解析】①当点P在BC上时,如图1,
若△APC的面积等于△ABC面积的一半,则 CP=此时,点P移动的距离为AC+CP=12+ 移动的时间为 (秒).
②当点P在BA上时,如图2,
若△APC的面积等于△ABC面积的一半,则点 P为BA的中点,
此时,点 P移动的距离为AC+CB+BP=12+9+
移动的时间为 (秒).
故答案为 或
(2)△APQ≌△DEF,对应顶点为 A与D,P与E,Q与F.
①当点 P在AC上,如图3所示.
此时AP=4,AQ=5,所以点Q移动的速度为5÷(4÷3)
②当点 P在AB上,如图4所示.此时,AP=4,AQ=5,
点 P移动的距离为9+12+15-4=32(cm),点 Q移动的距离为9+12+15-5=31(cm),
所以点Q移动的速度为 综上所述,两点运动过程中的某一时刻,恰好△APQ≌△DEF,点Q的运动速度为 或
23.解:(1)由题意可设y =k x+80(k ≠0).
图象过点(1,95),则有95=k +80.
所以k =15.所以y =15x+80(x≥0).
由题意,得 y =30x(x≥0).
(2)当y =y 时,15x+80=30x,解得 所以当租车
时间为 小时时,选择甲、乙公司一样合算;
当租车时间小于 小时时,选择乙公司合算;
当租车时间大于 小时时,选择甲公司合算.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
