6《平行四边形的面积》(教案)-五年级数学上册人教版
文档属性
| 名称 | 6《平行四边形的面积》(教案)-五年级数学上册人教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 200.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-24 00:00:00 | ||
图片预览

文档简介
6《平行四边形的面积》教学设计
教学内容:
人教版五年级上册第六单元《平行四边形的面积》。
教学目标:
1.学生通过动手操作、实验观察等方法,探索并掌握平行四边形面积计算公式。
2.学生会用面积公式计算平行四边形的面积,并能解决生活中的简单实际问题。
3.学生经历平行四边形面积计算公式的推导过程,感受转化的数学思想,促进学生空间观念的发展。
4.在学习过程中,让学生获得成功的体验,树立学习的信心。
教学重点:
学生理解平行四边形的面积公式并正确计算。
教学难点:
学生经历平行四边形面积计算公式的推导过程。
教学准备:
课件、前置作业,方格纸、平行四边形纸片。
前置作业:
1.我会直接数出平行四边形的面积。
(提示:一个方格代表 1平方米,不满一格的都按半格计算。满格的请在格子里打√,半格的请在格子里画○)
我直接数出这个平行四边形中有()个满格,有()个半格;所以这个平行四边形的面积是()平方米。
2.我会用分一分,拼一拼等方法数出平行四边形的面积。在图中画一画、补一补。
我用分一分、拼一拼等方法数出平行四边形的面积是()平方米。
教学过程:
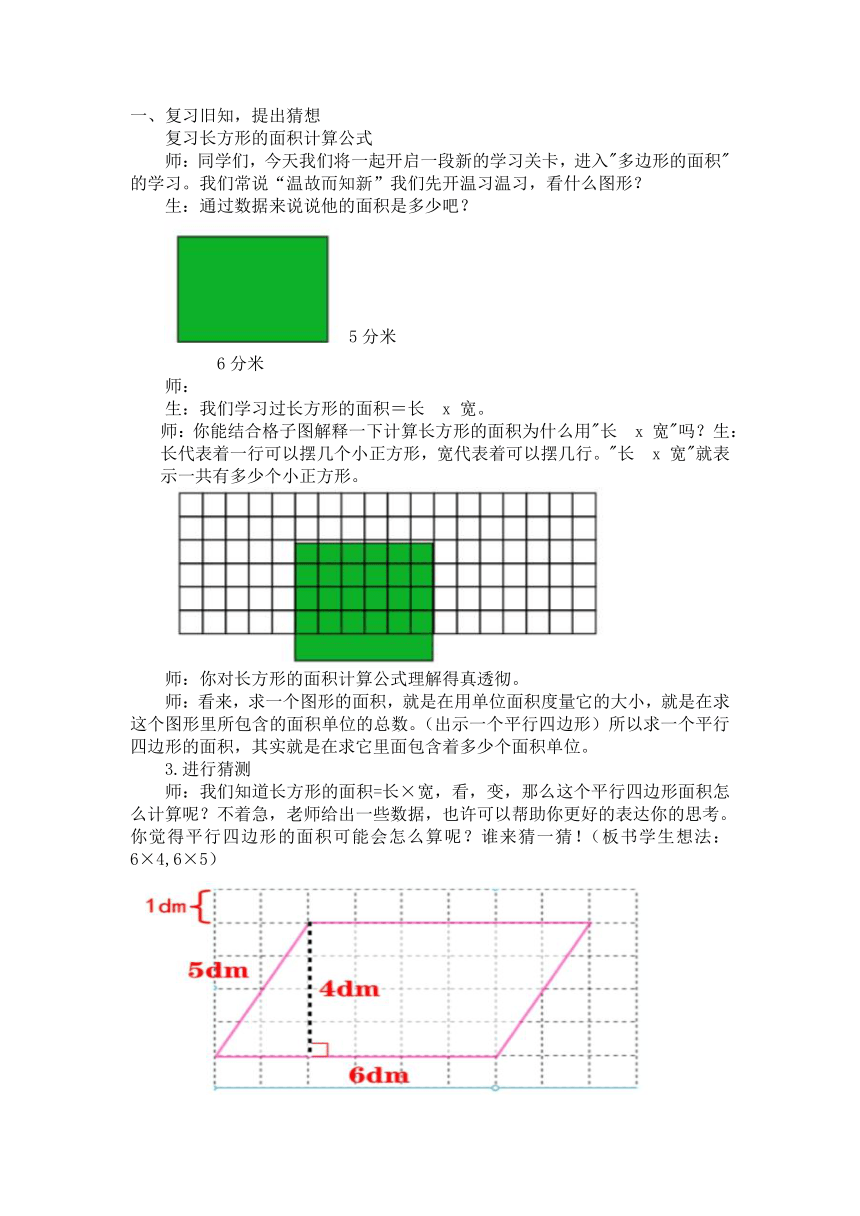
一、复习旧知,提出猜想
复习长方形的面积计算公式
师:同学们,今天我们将一起开启一段新的学习关卡,进入"多边形的面积"的学习。我们常说“温故而知新”我们先开温习温习,看什么图形?
生:通过数据来说说他的面积是多少吧?
5分米
6分米
师:
生:我们学习过长方形的面积=长 x 宽。
师:你能结合格子图解释一下计算长方形的面积为什么用"长 x 宽"吗?生:长代表着一行可以摆几个小正方形,宽代表着可以摆几行。"长 x 宽"就表示一共有多少个小正方形。
师:你对长方形的面积计算公式理解得真透彻。
师:看来,求一个图形的面积,就是在用单位面积度量它的大小,就是在求这个图形里所包含的面积单位的总数。(出示一个平行四边形)所以求一个平行四边形的面积,其实就是在求它里面包含着多少个面积单位。
3.进行猜测
师:我们知道长方形的面积=长×宽,看,变,那么这个平行四边形面积怎么计算呢?不着急,老师给出一些数据,也许可以帮助你更好的表达你的思考。你觉得平行四边形的面积可能会怎么算呢?谁来猜一猜!(板书学生想法:6×4,6×5)
生:我想它的面积是 24平方分米,算式是 6x4,也就是用"底 x 高"计算。师:你是一个敢于表达自己想法的学生,谁还有不同的想法?
生:我想它的面积可能是 27平方米,用 6x5计算。
师:也就是用"底 x 邻边"计算。你敢于发出不同的声音,老师欣赏你。这就是我们这节课探究的内容:平行四边形的面积。(黑板上摆一个平行四边形,板书课题)
二、多样方法,验证猜想
师:同学们,伟大的发现总是从猜想开始的。但有了猜想,我们还要验证,这样才能去伪存真,我们该怎么验证平行四边形的面积到底是底乘高等于 24,还是底乘邻边等于 27呢?
生:可以用数格子的方法。
师:利用格子图清清楚楚数出它的面积。
师:为了大家验证方便,老师请来了方格纸帮忙,每个方格就是 1平方米。请利于5dm 6dm 4dm
用带有小方格的平行四边形开始你的验证吧。
1.数格子的验证方法学生展示
师:你们都很善于观察、思考,把不好数的平行四边形的面积转化成长方形的面积,巧妙解决了困难。你们太棒了,老师你们点赞。
师:仔细观察算式数据和图形,你有什么结论吗?
生:平行四边形的面积等于底乘高
师:看来用谁乘谁就能算出平行四边形的面积
生:底乘高!
师:这件事情突然变得简单了,可是这会不会是一个巧合,所有的平行四边形的面积都等于底乘高吗?
师:那你能证明吗?
生:能!
2.剪拼验证师:该如何验证呢?生:把平行四边形剪拼成长方形师:你们的意思是动手剪一剪,然后拼一拼,看看能有什么发现。那我们动手试一试。请看操作要求。
(1)把平行四边形剪拼成长方形。(先标出底和高,再剪拼)
(2)观察原来的平行四边形和转化后的长方形,你发现了它们之间有联系?
(3)组内交流想法并完成探究单。
师:看的出大家的讨论非常热烈,哪个小组愿意第一个向全班同学展示你们的汇报你们组的智慧。有一个小小的要求,小组内推荐两名组员上台展示,一个人负责说,一个人负责操作演示。学生汇报。
生 1:我们是这样剪拼的:沿着高剪下一个直角三角形,然后平移拼成长方形。平行四边形的面积等于长方形的面积,平行四边形的底等于长方形的长,平行四边形的高等于长方形的宽。师:其他人听懂了吗?还有不同的想法吗?
生 2:我们是这样剪拼的:沿着高剪下两个直角梯形,然后平移拼成长方形。平行四边形的面积等于长方形的面积,平行四边形的底相当于长方形的长,平行四边形的高相当于长方形的宽。
师:老师还有一种剪法,大家看看怎么样?(故意沿着不是高的一条线剪开后拼)
生:这样剪不行,因为你拼成的还是平行四边形,只有拼成长方形我们才会计算面积。
师:大家认为一定要把不会计算面积的平行四边形转化成会计算的长方形才可以。那我该怎样剪才会拼成一个长方形呢?
生:要沿着高剪开才会拼成长方形。师:为什么一定要沿着高剪开才会拼成长方形呢?
生:因为只有沿着高剪开,才能得到直角
师:原来沿着高剪开得到直角才是剪拼成长方形的关键。谁能再清楚的说说,我们怎样才能将平行四边形剪拼成一个长方形呢?
师:我们是不是只能沿着这条高剪开才能拼成长方形呢?
生 1:(指着右边的一条高)还可以沿着这条高剪开。
生 2:还可以沿着中间的一条高剪开。
生 3:可以沿着任意一条高剪开。 (相机板书转化)
师:你总结得真好。其他同学听懂了吗?
师:平行四边形有几种高,我们还可以以长为 5分米的这条边为底,沿这条底的高剪开,通过平移也可以得到长方形。
师:我们一起看一看平行四边形的其他转化方式吧。(网络画板演示)看来所以的平行四边形都能转化成长方形,你能完整的介绍一下剪拼的过程吗
三、公式推导,得出结论
师:同学们,让我们接着梳理,对比转化后的长方形与原平行四边形,你发现什么变了、什么没有变?
生:形状发生变化,面积没有发生变化。
师:除了面积没变,我们还发现了他们的联系:(拼成的长方形的长就是原来平行四边形的底,长方形的宽就是原来平行四边形的高。长方形的面积计算公式是"长方形的面积=长 x 宽",也就是可以用"底 x 高"来计算平行四边形的面积。所以我们可以验证"平行四边形的面积=底 x 高")根据学生回答进行板书:
长方形的面积=长 × 宽
║ ║ ║
平行四边形面积=底 × 高
拓展:同学们,今天你探究平行四边形的面积的方法与我国魏晋时期的数学家刘徽的想法不谋而合,他曾在九章算术中记载:出入相补、以盈补虚面积计算方法,就是把一个图形分割、移补,但面积不变,来计算它的面积。这就是割补法。
师:回忆一下,刚才我们是怎么一步一步地研究推导出平行四边形面积的计算的?
生总结转化过程(师相机板贴 联系 推理 公式)框架佐证
师:我们利用割补法将平行四边形转化成长方形,推导出了公式。那我可以直接拉成平行四边形或长方形吗?(实物演示)我们一起来看一下(网络画板演示)在推拉的过程中图形的什么没变,什么变了?
生:周长没变,高发生变化,面积发生变化。
师:你具备了锐利的数学眼光,现在我们可以确定平行四边形的面积与底和谁有关?(高)孩子们我们可以更加自信的大声说出平行四边形的面积公式是:平行四边形面积=底 × 高(生齐读)
师:数学讲究简明,我们可以用什么来表示平行四边形的面积公式。
生:字母
师:英雄所见略同,数学家也是这样想的,
如果用 S 表示平行四边形的面积。 a 表示底, h 表示底边 a 上的高,那么平行四边形的面积计算公式用字母怎么表示。生(板演) S = ah
四、巩固练习,能力提升
师:恭喜大家解锁了新图形的面积计算公式,你能解决数学书例一的问题吗?
1. 平行四边形花坛的底是 6m,高是 4m,它的面积是多少?先来看一下解题思路。如果老师沿对角线将花坛分成两块,你能算出两块花坛的面积各是多少吗?这两块花坛各是什么图形?三角形的面积计算呼之欲出啊,这是我们下节课的学习内容。
2.接下来完成本节课的当堂检测
做此类题时,要注意什么。
3.拓展题
五、回顾整理,总结方法
师:我们来理一理今天的研究思路。遇到一个新问题,同学们首先提出了自己的猜想,然后用数格子、割补法进行验证,经历了把平行四边形转化成长方形,然后利用转化前后图形的联系,推导出公式的探究过程,并利用平行四边形的框架进一步佐证平行四边形的面积等于底乘高,最终得出结论。你经过思考实现了数与不数的跨越。孩子们你有什么收获呢?
生说收获
师:同学们,看似不同的图形却又有着千丝万缕的关系,数学是多么的奇妙呀!那么我们今后学习的三角形、梯形的面积会不会也藏着这样的秘密,期待大家继续去研究发现。
教学内容:
人教版五年级上册第六单元《平行四边形的面积》。
教学目标:
1.学生通过动手操作、实验观察等方法,探索并掌握平行四边形面积计算公式。
2.学生会用面积公式计算平行四边形的面积,并能解决生活中的简单实际问题。
3.学生经历平行四边形面积计算公式的推导过程,感受转化的数学思想,促进学生空间观念的发展。
4.在学习过程中,让学生获得成功的体验,树立学习的信心。
教学重点:
学生理解平行四边形的面积公式并正确计算。
教学难点:
学生经历平行四边形面积计算公式的推导过程。
教学准备:
课件、前置作业,方格纸、平行四边形纸片。
前置作业:
1.我会直接数出平行四边形的面积。
(提示:一个方格代表 1平方米,不满一格的都按半格计算。满格的请在格子里打√,半格的请在格子里画○)
我直接数出这个平行四边形中有()个满格,有()个半格;所以这个平行四边形的面积是()平方米。
2.我会用分一分,拼一拼等方法数出平行四边形的面积。在图中画一画、补一补。
我用分一分、拼一拼等方法数出平行四边形的面积是()平方米。
教学过程:
一、复习旧知,提出猜想
复习长方形的面积计算公式
师:同学们,今天我们将一起开启一段新的学习关卡,进入"多边形的面积"的学习。我们常说“温故而知新”我们先开温习温习,看什么图形?
生:通过数据来说说他的面积是多少吧?
5分米
6分米
师:
生:我们学习过长方形的面积=长 x 宽。
师:你能结合格子图解释一下计算长方形的面积为什么用"长 x 宽"吗?生:长代表着一行可以摆几个小正方形,宽代表着可以摆几行。"长 x 宽"就表示一共有多少个小正方形。
师:你对长方形的面积计算公式理解得真透彻。
师:看来,求一个图形的面积,就是在用单位面积度量它的大小,就是在求这个图形里所包含的面积单位的总数。(出示一个平行四边形)所以求一个平行四边形的面积,其实就是在求它里面包含着多少个面积单位。
3.进行猜测
师:我们知道长方形的面积=长×宽,看,变,那么这个平行四边形面积怎么计算呢?不着急,老师给出一些数据,也许可以帮助你更好的表达你的思考。你觉得平行四边形的面积可能会怎么算呢?谁来猜一猜!(板书学生想法:6×4,6×5)
生:我想它的面积是 24平方分米,算式是 6x4,也就是用"底 x 高"计算。师:你是一个敢于表达自己想法的学生,谁还有不同的想法?
生:我想它的面积可能是 27平方米,用 6x5计算。
师:也就是用"底 x 邻边"计算。你敢于发出不同的声音,老师欣赏你。这就是我们这节课探究的内容:平行四边形的面积。(黑板上摆一个平行四边形,板书课题)
二、多样方法,验证猜想
师:同学们,伟大的发现总是从猜想开始的。但有了猜想,我们还要验证,这样才能去伪存真,我们该怎么验证平行四边形的面积到底是底乘高等于 24,还是底乘邻边等于 27呢?
生:可以用数格子的方法。
师:利用格子图清清楚楚数出它的面积。
师:为了大家验证方便,老师请来了方格纸帮忙,每个方格就是 1平方米。请利于5dm 6dm 4dm
用带有小方格的平行四边形开始你的验证吧。
1.数格子的验证方法学生展示
师:你们都很善于观察、思考,把不好数的平行四边形的面积转化成长方形的面积,巧妙解决了困难。你们太棒了,老师你们点赞。
师:仔细观察算式数据和图形,你有什么结论吗?
生:平行四边形的面积等于底乘高
师:看来用谁乘谁就能算出平行四边形的面积
生:底乘高!
师:这件事情突然变得简单了,可是这会不会是一个巧合,所有的平行四边形的面积都等于底乘高吗?
师:那你能证明吗?
生:能!
2.剪拼验证师:该如何验证呢?生:把平行四边形剪拼成长方形师:你们的意思是动手剪一剪,然后拼一拼,看看能有什么发现。那我们动手试一试。请看操作要求。
(1)把平行四边形剪拼成长方形。(先标出底和高,再剪拼)
(2)观察原来的平行四边形和转化后的长方形,你发现了它们之间有联系?
(3)组内交流想法并完成探究单。
师:看的出大家的讨论非常热烈,哪个小组愿意第一个向全班同学展示你们的汇报你们组的智慧。有一个小小的要求,小组内推荐两名组员上台展示,一个人负责说,一个人负责操作演示。学生汇报。
生 1:我们是这样剪拼的:沿着高剪下一个直角三角形,然后平移拼成长方形。平行四边形的面积等于长方形的面积,平行四边形的底等于长方形的长,平行四边形的高等于长方形的宽。师:其他人听懂了吗?还有不同的想法吗?
生 2:我们是这样剪拼的:沿着高剪下两个直角梯形,然后平移拼成长方形。平行四边形的面积等于长方形的面积,平行四边形的底相当于长方形的长,平行四边形的高相当于长方形的宽。
师:老师还有一种剪法,大家看看怎么样?(故意沿着不是高的一条线剪开后拼)
生:这样剪不行,因为你拼成的还是平行四边形,只有拼成长方形我们才会计算面积。
师:大家认为一定要把不会计算面积的平行四边形转化成会计算的长方形才可以。那我该怎样剪才会拼成一个长方形呢?
生:要沿着高剪开才会拼成长方形。师:为什么一定要沿着高剪开才会拼成长方形呢?
生:因为只有沿着高剪开,才能得到直角
师:原来沿着高剪开得到直角才是剪拼成长方形的关键。谁能再清楚的说说,我们怎样才能将平行四边形剪拼成一个长方形呢?
师:我们是不是只能沿着这条高剪开才能拼成长方形呢?
生 1:(指着右边的一条高)还可以沿着这条高剪开。
生 2:还可以沿着中间的一条高剪开。
生 3:可以沿着任意一条高剪开。 (相机板书转化)
师:你总结得真好。其他同学听懂了吗?
师:平行四边形有几种高,我们还可以以长为 5分米的这条边为底,沿这条底的高剪开,通过平移也可以得到长方形。
师:我们一起看一看平行四边形的其他转化方式吧。(网络画板演示)看来所以的平行四边形都能转化成长方形,你能完整的介绍一下剪拼的过程吗
三、公式推导,得出结论
师:同学们,让我们接着梳理,对比转化后的长方形与原平行四边形,你发现什么变了、什么没有变?
生:形状发生变化,面积没有发生变化。
师:除了面积没变,我们还发现了他们的联系:(拼成的长方形的长就是原来平行四边形的底,长方形的宽就是原来平行四边形的高。长方形的面积计算公式是"长方形的面积=长 x 宽",也就是可以用"底 x 高"来计算平行四边形的面积。所以我们可以验证"平行四边形的面积=底 x 高")根据学生回答进行板书:
长方形的面积=长 × 宽
║ ║ ║
平行四边形面积=底 × 高
拓展:同学们,今天你探究平行四边形的面积的方法与我国魏晋时期的数学家刘徽的想法不谋而合,他曾在九章算术中记载:出入相补、以盈补虚面积计算方法,就是把一个图形分割、移补,但面积不变,来计算它的面积。这就是割补法。
师:回忆一下,刚才我们是怎么一步一步地研究推导出平行四边形面积的计算的?
生总结转化过程(师相机板贴 联系 推理 公式)框架佐证
师:我们利用割补法将平行四边形转化成长方形,推导出了公式。那我可以直接拉成平行四边形或长方形吗?(实物演示)我们一起来看一下(网络画板演示)在推拉的过程中图形的什么没变,什么变了?
生:周长没变,高发生变化,面积发生变化。
师:你具备了锐利的数学眼光,现在我们可以确定平行四边形的面积与底和谁有关?(高)孩子们我们可以更加自信的大声说出平行四边形的面积公式是:平行四边形面积=底 × 高(生齐读)
师:数学讲究简明,我们可以用什么来表示平行四边形的面积公式。
生:字母
师:英雄所见略同,数学家也是这样想的,
如果用 S 表示平行四边形的面积。 a 表示底, h 表示底边 a 上的高,那么平行四边形的面积计算公式用字母怎么表示。生(板演) S = ah
四、巩固练习,能力提升
师:恭喜大家解锁了新图形的面积计算公式,你能解决数学书例一的问题吗?
1. 平行四边形花坛的底是 6m,高是 4m,它的面积是多少?先来看一下解题思路。如果老师沿对角线将花坛分成两块,你能算出两块花坛的面积各是多少吗?这两块花坛各是什么图形?三角形的面积计算呼之欲出啊,这是我们下节课的学习内容。
2.接下来完成本节课的当堂检测
做此类题时,要注意什么。
3.拓展题
五、回顾整理,总结方法
师:我们来理一理今天的研究思路。遇到一个新问题,同学们首先提出了自己的猜想,然后用数格子、割补法进行验证,经历了把平行四边形转化成长方形,然后利用转化前后图形的联系,推导出公式的探究过程,并利用平行四边形的框架进一步佐证平行四边形的面积等于底乘高,最终得出结论。你经过思考实现了数与不数的跨越。孩子们你有什么收获呢?
生说收获
师:同学们,看似不同的图形却又有着千丝万缕的关系,数学是多么的奇妙呀!那么我们今后学习的三角形、梯形的面积会不会也藏着这样的秘密,期待大家继续去研究发现。
