24.2.1 点和圆的位置关系一课一练(含解析)
文档属性
| 名称 | 24.2.1 点和圆的位置关系一课一练(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-26 11:20:18 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
24.2.1 点和圆的位置关系一课一练
一、填空题
1.已知: ,求作 的外接圆,作法:①分别作线段BC,AC的垂直平分线EF和MN,它们交于点O;②以点O为圆心,OB的长为半径画弧,如图⊙O即为所求,以上作图用到的数学依据是 .
2.如图,已知正方形ABCD的边长为4,点E是正方形内部一点,连接BE,CE,且∠ABE=∠BCE,点F是AB边上一动点,连接FD,FE,则FD+FE的长度最小值为 .
二、单选题
3.设P为⊙O外一点,若点P到⊙O的最短距离为3,最长距离为7,则⊙O的半径为( )
A.3 B.2 C.4或10 D.2或5
4.已知⊙O的半径为3cm,且点P在⊙O外,则线段PO的长度为( )
A.等于6cm B.大于3cm C.小于3cm D.等于3cm
5.下列说法:①三点确定一个圆;②相等的圆周角所对的弧相等;③同圆或等圆中,等弦所对的弧相等;④等边三角形的内心与外心重合;⑤三角形的外心到三角形各顶点距离相等其中,正确的个数共有( )
A.1 B.2 C.3 D.4
6.若的半径为,点P到圆心O的距离,则点P的位置是( )
A.在内 B.在上 C.在外 D.不能确定
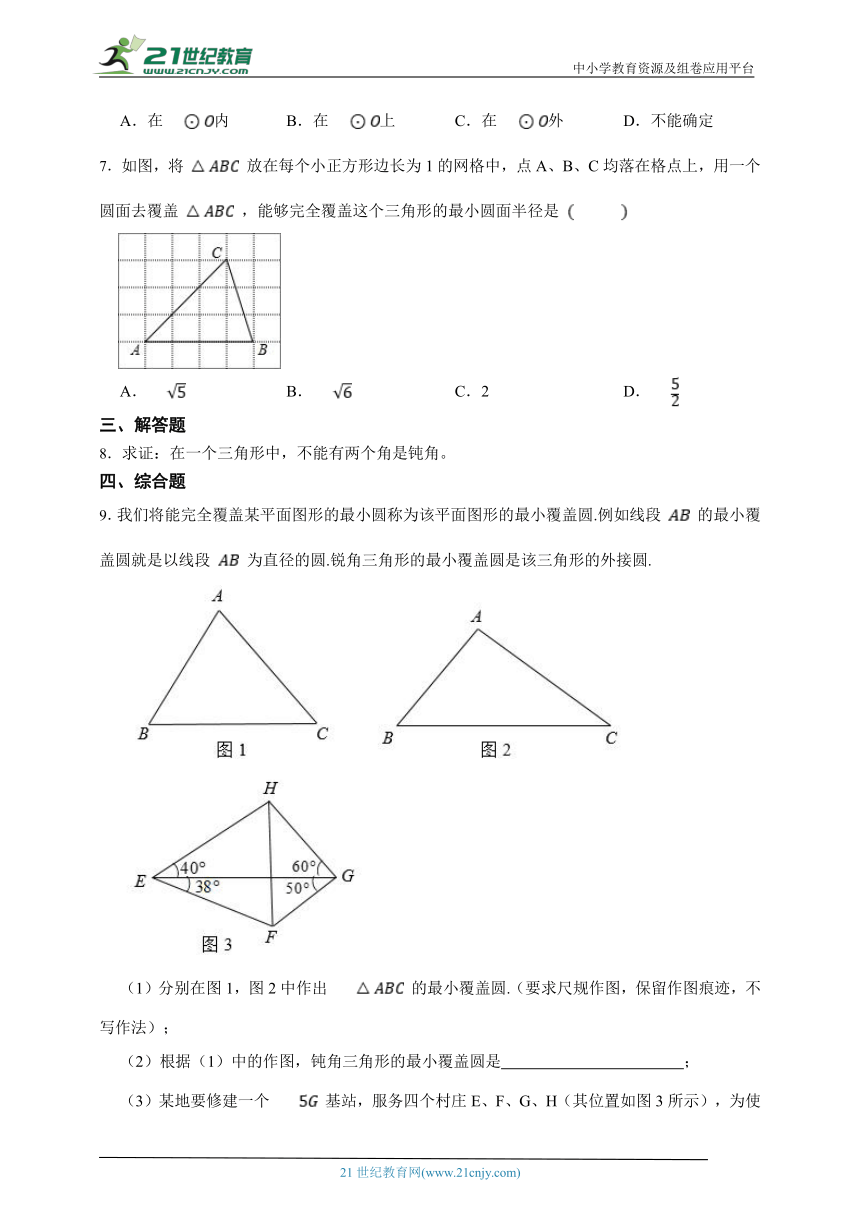
7.如图,将 放在每个小正方形边长为1的网格中,点A、B、C均落在格点上,用一个圆面去覆盖 ,能够完全覆盖这个三角形的最小圆面半径是
A. B. C.2 D.
三、解答题
8.求证:在一个三角形中,不能有两个角是钝角。
四、综合题
9.我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段 的最小覆盖圆就是以线段 为直径的圆.锐角三角形的最小覆盖圆是该三角形的外接圆.
(1)分别在图1,图2中作出 的最小覆盖圆.(要求尺规作图,保留作图痕迹,不写作法);
(2)根据(1)中的作图,钝角三角形的最小覆盖圆是 ;
(3)某地要修建一个 基站,服务四个村庄E、F、G、H(其位置如图3所示),为使信号可以覆盖四个村庄,且基站所需发射功率最小(距离越小,所需功率越小),此基站应建在何处?请说明理由.
五、实践探究题
10.
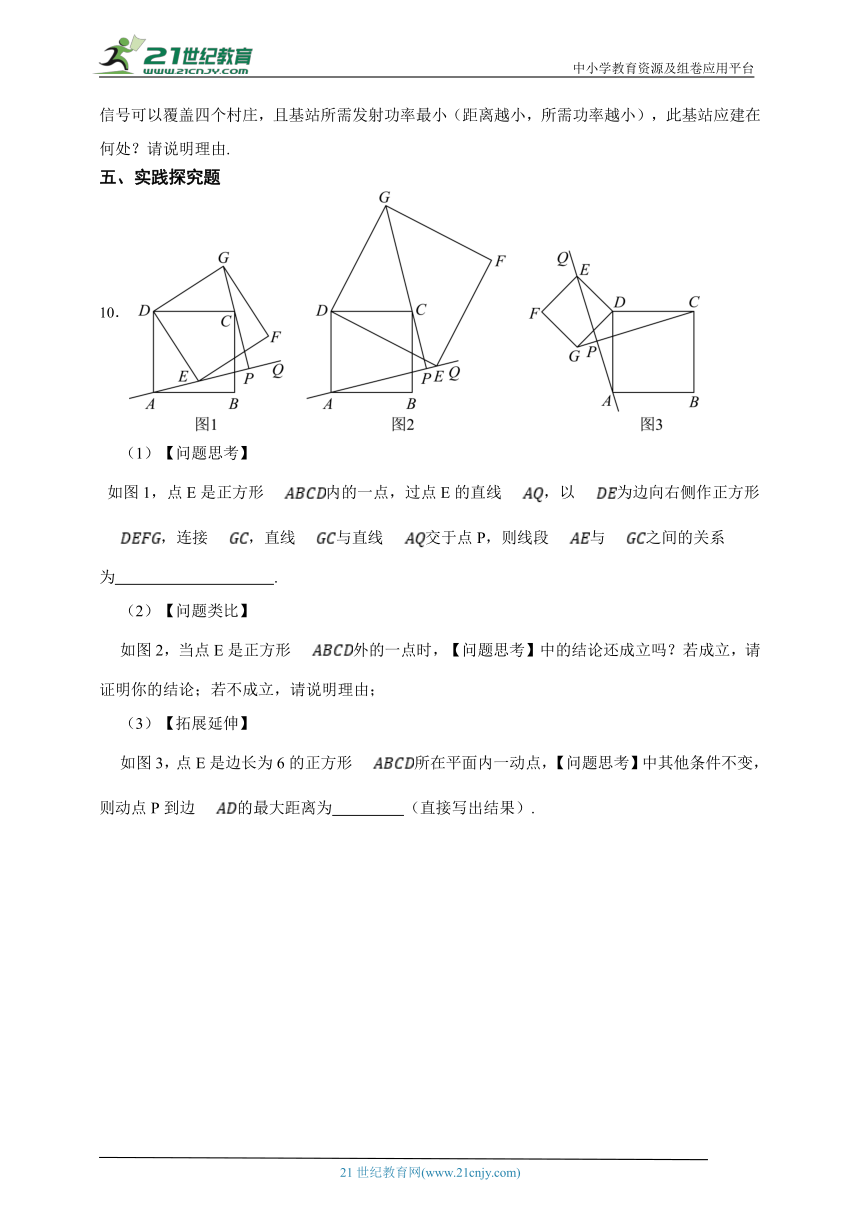
(1)【问题思考】
如图1,点E是正方形内的一点,过点E的直线,以为边向右侧作正方形,连接,直线与直线交于点P,则线段与之间的关系为 .
(2)【问题类比】
如图2,当点E是正方形外的一点时,【问题思考】中的结论还成立吗?若成立,请证明你的结论;若不成立,请说明理由;
(3)【拓展延伸】
如图3,点E是边长为6的正方形所在平面内一动点,【问题思考】中其他条件不变,则动点P到边的最大距离为 (直接写出结果).
答案解析部分
1.【答案】线段的垂直平分线的性质
【解析】【解答】解:如图,连接 ,
∵点O为AC和BC的垂直平分线的交点,
∴OA=OC=OB,
∴⊙O为 的外接圆.
故答案为:线段的垂直平分线的性质.
【分析】利用线段垂直平分线的性质得到OA=OC=OB,然后根据点与圆的位置关系可判断点A、C在⊙O上.
2.【答案】2-2
【解析】【解答】解:∵四边形ABCD是正方形,
∴∠ABC=90°,
∴∠ABE+∠CBE=90°,
∵∠ABE=∠BCE,
∴∠BCE+∠CBE=90°,
∴∠BEC=90°,
∴点E在以BC为直径的半圆上移动,
如图,设BC的中点为O,作正方形ABCD关于直线AB对称的正方形APGB,则点D的对应点是P,
连接PO交AB于F,交半圆O于E,则线段EP的长即为FD+FE的长度最小值,OE=4,
∵∠G=90°,PG=BG=AB=4,
∴OG=6,
∴OP==,
∴EP=-2,
∴FD+FE的长度最小值为-2.
故答案为:2-2.
【分析】根据正方形的性质可得∠ABC=90°,由已知条件可得∠ABE=∠BCE,结合∠ABE+∠CBE=90°可得∠BEC=90°,则点E在以BC为直径的半圆上移动,设BC的中点为O,作正方形ABCD关于直线AB对称的正方形APGB,则点D的对应点是P,连接PO交AB于F,交半圆O于E,则线段EP的长即为FD+FE的长度最小值,OE=4,易得OG=6,利用勾股定理求出OP,进而可得EP,据此解答.
3.【答案】B
【解析】【解答】解:∵P为⊙O外一点,若点P到⊙O的最短距离为3,最长距离为7,
∴⊙O的直径为:7-3=4,
∴⊙O的半径为2,
故答案为:B.
【分析】由圆外一点到圆的最远距离与最近距离的差就是该圆的直径,即可算出答案。
4.【答案】B
【解析】【解答】解:点P在圆外,则点到圆心的距离大于圆的半径,
即: cm.
故答案为:B.
【分析】设点到圆心的距离为d,圆的半径为r,则 时,点在圆外;当 时,点在圆上;当 时,点在圆内.
5.【答案】B
【解析】【解答】解:不共线的三点确定一个圆,所以①错误;
在同圆或等圆中,相等的圆周角所对的弧相等,所以②错误;
同圆或等圆中,等弦所对的优弧或劣弧对应相等,所以③错误;
等边三角形的内心与外心重合,所以④正确;
三角形的外心到三角形各顶点的距离都相等,所以⑤正确.
故答案为:B.
【分析】根据确定圆的条件对①进行判断;根据圆周角定理对②进行判断;根据圆心角、弧、弦的关系对③进行判断;根据等边三角形的性质和三角形内心、外心的定义对④⑤进行判断.
6.【答案】C
【解析】【解答】解:∵圆O的半径为6cm,点P到圆心O的距离PO=8cm,6<8,
∴点P在圆O外,
故答案为:C.
【分析】设圆的半径为r,点到圆心的距离为d,当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内,据此判断即可得出答案.
7.【答案】A
【解析】【解答】解:如图所示:
点O为 外接圆圆心,则AO为外接圆半径,
故能够完全覆盖这个三角形的最小圆面的半径是: .
故答案为:A.
【分析】作出线段AB、AC的垂直平分线,其交点即为外接圆的圆心,结合勾股定理可求出圆的半径.
8.【答案】解:已知△ABC.
求证:∠A,∠B,∠C中不能有两个角是钝角.
证明:假设∠A,∠B,∠C中有两个角是钝角,不妨设∠A>90°,∠B>90°,
∴∠A+∠B+∠C>90°+90°+∠C>180°,这与“三角形内角和为180°”矛盾,
∴假设不成立,即在一个三角形中,不能有两个角是钝角。
【解析】【分析】根据反证法的证明方法,先假设∠A,∠B,∠C中有两个角是钝角,然后根据三角形内角和定理证明即可.
9.【答案】(1)解:作图如下图所示;
(2)以最长边为直径的圆
(3)解: 的外心(外接圆的圆心)
理由:如图, 的外接圆刚好覆盖E,F,H三点,与直线 交于点D,连接DH和DF
∵ ,
且 ,
∴ ,
∵∠HGF=50°+60°=110°,
∴ .
∴点G在点E,D之间.
即点G被外接圆覆盖,
此时该圆为能完全覆盖该四边形的最小圆.
因此,此基站应建在 的外心处.
【解析】【解答】解:(2)以最长边为直径的圆;
理由:∵线段 的最小覆盖圆就是以线段 为直径的圆,
由于∠A为钝角,因此∠A在圆内,
∴该圆为能完全覆盖该钝角三角形的最小圆.
【分析】(1)作出图1中任意两边的垂直平分线,其交点即为圆心,再以该点到三角形任意一个顶点之间的线段为半径画圆即可;作出图2中最长边的垂直平分线得到它的中点,再以中点为圆心,以这条最长边的一半长为半径作圆即可;
(2)依据最小覆盖圆的定义判断即可;
(3)先得到 的外接圆刚好覆盖E,F,H三点,再说明G点在圆内即可.
10.【答案】(1),
(2)解:问题思考中的结论仍然成立,理由如下:
设和交于点H,
∵四边形和四边形都为正方形,
∴,,
∴,
即,
∴,
∴,,
∵,
∴,
即,
∵,
∴,
即,
故答案为:,;
(3)
【解析】【解答】解:(1)设和交于点H,
∵四边形和四边形都为正方形,
∴,,
∴,
即,
∴,
∴,,
∵,
∴,
即,
∵,
∴,
即,
故答案为:,;
(3)∵,
∴点P的运用轨迹即为以为直径的上,
如图:
当点P位于右侧,且经过圆心O时,动点P到边的距离最大,
∵正方形的边长为,
∴,,
∴,
∴,
即动点P到边的最大距离为,
故答案为:.
【分析】【问题思考】设AQ和BC交于点H,由正方形的性质可得∠ADC=∠EDG=90°,DA=DC,DE=DG,根据角的和差关系可得∠ADE=∠CDG,利用SAS证明△DAE≌△DCG,得到AE=CG,∠DAE=∠DCG,根据等角的余角相等可得∠BAH=∠PCH,结合∠AHB=∠CHP可得∠B=∠CPA=90°,据此解答;
【问题类比】同上进行解答;
【拓展延伸】 由题意可得:点P的运用轨迹即为以AC为直径的⊙O上,当点P位于AD右侧,PH⊥AD且经过圆心O时,动点P到边AD的距离最大,由正方形的边长可得AC、OH、OP、PH的值,据此解答.
24.2.1 点和圆的位置关系一课一练
一、填空题
1.已知: ,求作 的外接圆,作法:①分别作线段BC,AC的垂直平分线EF和MN,它们交于点O;②以点O为圆心,OB的长为半径画弧,如图⊙O即为所求,以上作图用到的数学依据是 .
2.如图,已知正方形ABCD的边长为4,点E是正方形内部一点,连接BE,CE,且∠ABE=∠BCE,点F是AB边上一动点,连接FD,FE,则FD+FE的长度最小值为 .
二、单选题
3.设P为⊙O外一点,若点P到⊙O的最短距离为3,最长距离为7,则⊙O的半径为( )
A.3 B.2 C.4或10 D.2或5
4.已知⊙O的半径为3cm,且点P在⊙O外,则线段PO的长度为( )
A.等于6cm B.大于3cm C.小于3cm D.等于3cm
5.下列说法:①三点确定一个圆;②相等的圆周角所对的弧相等;③同圆或等圆中,等弦所对的弧相等;④等边三角形的内心与外心重合;⑤三角形的外心到三角形各顶点距离相等其中,正确的个数共有( )
A.1 B.2 C.3 D.4
6.若的半径为,点P到圆心O的距离,则点P的位置是( )
A.在内 B.在上 C.在外 D.不能确定
7.如图,将 放在每个小正方形边长为1的网格中,点A、B、C均落在格点上,用一个圆面去覆盖 ,能够完全覆盖这个三角形的最小圆面半径是
A. B. C.2 D.
三、解答题
8.求证:在一个三角形中,不能有两个角是钝角。
四、综合题
9.我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段 的最小覆盖圆就是以线段 为直径的圆.锐角三角形的最小覆盖圆是该三角形的外接圆.
(1)分别在图1,图2中作出 的最小覆盖圆.(要求尺规作图,保留作图痕迹,不写作法);
(2)根据(1)中的作图,钝角三角形的最小覆盖圆是 ;
(3)某地要修建一个 基站,服务四个村庄E、F、G、H(其位置如图3所示),为使信号可以覆盖四个村庄,且基站所需发射功率最小(距离越小,所需功率越小),此基站应建在何处?请说明理由.
五、实践探究题
10.
(1)【问题思考】
如图1,点E是正方形内的一点,过点E的直线,以为边向右侧作正方形,连接,直线与直线交于点P,则线段与之间的关系为 .
(2)【问题类比】
如图2,当点E是正方形外的一点时,【问题思考】中的结论还成立吗?若成立,请证明你的结论;若不成立,请说明理由;
(3)【拓展延伸】
如图3,点E是边长为6的正方形所在平面内一动点,【问题思考】中其他条件不变,则动点P到边的最大距离为 (直接写出结果).
答案解析部分
1.【答案】线段的垂直平分线的性质
【解析】【解答】解:如图,连接 ,
∵点O为AC和BC的垂直平分线的交点,
∴OA=OC=OB,
∴⊙O为 的外接圆.
故答案为:线段的垂直平分线的性质.
【分析】利用线段垂直平分线的性质得到OA=OC=OB,然后根据点与圆的位置关系可判断点A、C在⊙O上.
2.【答案】2-2
【解析】【解答】解:∵四边形ABCD是正方形,
∴∠ABC=90°,
∴∠ABE+∠CBE=90°,
∵∠ABE=∠BCE,
∴∠BCE+∠CBE=90°,
∴∠BEC=90°,
∴点E在以BC为直径的半圆上移动,
如图,设BC的中点为O,作正方形ABCD关于直线AB对称的正方形APGB,则点D的对应点是P,
连接PO交AB于F,交半圆O于E,则线段EP的长即为FD+FE的长度最小值,OE=4,
∵∠G=90°,PG=BG=AB=4,
∴OG=6,
∴OP==,
∴EP=-2,
∴FD+FE的长度最小值为-2.
故答案为:2-2.
【分析】根据正方形的性质可得∠ABC=90°,由已知条件可得∠ABE=∠BCE,结合∠ABE+∠CBE=90°可得∠BEC=90°,则点E在以BC为直径的半圆上移动,设BC的中点为O,作正方形ABCD关于直线AB对称的正方形APGB,则点D的对应点是P,连接PO交AB于F,交半圆O于E,则线段EP的长即为FD+FE的长度最小值,OE=4,易得OG=6,利用勾股定理求出OP,进而可得EP,据此解答.
3.【答案】B
【解析】【解答】解:∵P为⊙O外一点,若点P到⊙O的最短距离为3,最长距离为7,
∴⊙O的直径为:7-3=4,
∴⊙O的半径为2,
故答案为:B.
【分析】由圆外一点到圆的最远距离与最近距离的差就是该圆的直径,即可算出答案。
4.【答案】B
【解析】【解答】解:点P在圆外,则点到圆心的距离大于圆的半径,
即: cm.
故答案为:B.
【分析】设点到圆心的距离为d,圆的半径为r,则 时,点在圆外;当 时,点在圆上;当 时,点在圆内.
5.【答案】B
【解析】【解答】解:不共线的三点确定一个圆,所以①错误;
在同圆或等圆中,相等的圆周角所对的弧相等,所以②错误;
同圆或等圆中,等弦所对的优弧或劣弧对应相等,所以③错误;
等边三角形的内心与外心重合,所以④正确;
三角形的外心到三角形各顶点的距离都相等,所以⑤正确.
故答案为:B.
【分析】根据确定圆的条件对①进行判断;根据圆周角定理对②进行判断;根据圆心角、弧、弦的关系对③进行判断;根据等边三角形的性质和三角形内心、外心的定义对④⑤进行判断.
6.【答案】C
【解析】【解答】解:∵圆O的半径为6cm,点P到圆心O的距离PO=8cm,6<8,
∴点P在圆O外,
故答案为:C.
【分析】设圆的半径为r,点到圆心的距离为d,当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内,据此判断即可得出答案.
7.【答案】A
【解析】【解答】解:如图所示:
点O为 外接圆圆心,则AO为外接圆半径,
故能够完全覆盖这个三角形的最小圆面的半径是: .
故答案为:A.
【分析】作出线段AB、AC的垂直平分线,其交点即为外接圆的圆心,结合勾股定理可求出圆的半径.
8.【答案】解:已知△ABC.
求证:∠A,∠B,∠C中不能有两个角是钝角.
证明:假设∠A,∠B,∠C中有两个角是钝角,不妨设∠A>90°,∠B>90°,
∴∠A+∠B+∠C>90°+90°+∠C>180°,这与“三角形内角和为180°”矛盾,
∴假设不成立,即在一个三角形中,不能有两个角是钝角。
【解析】【分析】根据反证法的证明方法,先假设∠A,∠B,∠C中有两个角是钝角,然后根据三角形内角和定理证明即可.
9.【答案】(1)解:作图如下图所示;
(2)以最长边为直径的圆
(3)解: 的外心(外接圆的圆心)
理由:如图, 的外接圆刚好覆盖E,F,H三点,与直线 交于点D,连接DH和DF
∵ ,
且 ,
∴ ,
∵∠HGF=50°+60°=110°,
∴ .
∴点G在点E,D之间.
即点G被外接圆覆盖,
此时该圆为能完全覆盖该四边形的最小圆.
因此,此基站应建在 的外心处.
【解析】【解答】解:(2)以最长边为直径的圆;
理由:∵线段 的最小覆盖圆就是以线段 为直径的圆,
由于∠A为钝角,因此∠A在圆内,
∴该圆为能完全覆盖该钝角三角形的最小圆.
【分析】(1)作出图1中任意两边的垂直平分线,其交点即为圆心,再以该点到三角形任意一个顶点之间的线段为半径画圆即可;作出图2中最长边的垂直平分线得到它的中点,再以中点为圆心,以这条最长边的一半长为半径作圆即可;
(2)依据最小覆盖圆的定义判断即可;
(3)先得到 的外接圆刚好覆盖E,F,H三点,再说明G点在圆内即可.
10.【答案】(1),
(2)解:问题思考中的结论仍然成立,理由如下:
设和交于点H,
∵四边形和四边形都为正方形,
∴,,
∴,
即,
∴,
∴,,
∵,
∴,
即,
∵,
∴,
即,
故答案为:,;
(3)
【解析】【解答】解:(1)设和交于点H,
∵四边形和四边形都为正方形,
∴,,
∴,
即,
∴,
∴,,
∵,
∴,
即,
∵,
∴,
即,
故答案为:,;
(3)∵,
∴点P的运用轨迹即为以为直径的上,
如图:
当点P位于右侧,且经过圆心O时,动点P到边的距离最大,
∵正方形的边长为,
∴,,
∴,
∴,
即动点P到边的最大距离为,
故答案为:.
【分析】【问题思考】设AQ和BC交于点H,由正方形的性质可得∠ADC=∠EDG=90°,DA=DC,DE=DG,根据角的和差关系可得∠ADE=∠CDG,利用SAS证明△DAE≌△DCG,得到AE=CG,∠DAE=∠DCG,根据等角的余角相等可得∠BAH=∠PCH,结合∠AHB=∠CHP可得∠B=∠CPA=90°,据此解答;
【问题类比】同上进行解答;
【拓展延伸】 由题意可得:点P的运用轨迹即为以AC为直径的⊙O上,当点P位于AD右侧,PH⊥AD且经过圆心O时,动点P到边AD的距离最大,由正方形的边长可得AC、OH、OP、PH的值,据此解答.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
24.2.1 点和圆的位置关系一课一练
一、填空题
1.已知: ,求作 的外接圆,作法:①分别作线段BC,AC的垂直平分线EF和MN,它们交于点O;②以点O为圆心,OB的长为半径画弧,如图⊙O即为所求,以上作图用到的数学依据是 .
2.如图,已知正方形ABCD的边长为4,点E是正方形内部一点,连接BE,CE,且∠ABE=∠BCE,点F是AB边上一动点,连接FD,FE,则FD+FE的长度最小值为 .
二、单选题
3.设P为⊙O外一点,若点P到⊙O的最短距离为3,最长距离为7,则⊙O的半径为( )
A.3 B.2 C.4或10 D.2或5
4.已知⊙O的半径为3cm,且点P在⊙O外,则线段PO的长度为( )
A.等于6cm B.大于3cm C.小于3cm D.等于3cm
5.下列说法:①三点确定一个圆;②相等的圆周角所对的弧相等;③同圆或等圆中,等弦所对的弧相等;④等边三角形的内心与外心重合;⑤三角形的外心到三角形各顶点距离相等其中,正确的个数共有( )
A.1 B.2 C.3 D.4
6.若的半径为,点P到圆心O的距离,则点P的位置是( )
A.在内 B.在上 C.在外 D.不能确定
7.如图,将 放在每个小正方形边长为1的网格中,点A、B、C均落在格点上,用一个圆面去覆盖 ,能够完全覆盖这个三角形的最小圆面半径是
A. B. C.2 D.
三、解答题
8.求证:在一个三角形中,不能有两个角是钝角。
四、综合题
9.我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段 的最小覆盖圆就是以线段 为直径的圆.锐角三角形的最小覆盖圆是该三角形的外接圆.
(1)分别在图1,图2中作出 的最小覆盖圆.(要求尺规作图,保留作图痕迹,不写作法);
(2)根据(1)中的作图,钝角三角形的最小覆盖圆是 ;
(3)某地要修建一个 基站,服务四个村庄E、F、G、H(其位置如图3所示),为使信号可以覆盖四个村庄,且基站所需发射功率最小(距离越小,所需功率越小),此基站应建在何处?请说明理由.
五、实践探究题
10.
(1)【问题思考】
如图1,点E是正方形内的一点,过点E的直线,以为边向右侧作正方形,连接,直线与直线交于点P,则线段与之间的关系为 .
(2)【问题类比】
如图2,当点E是正方形外的一点时,【问题思考】中的结论还成立吗?若成立,请证明你的结论;若不成立,请说明理由;
(3)【拓展延伸】
如图3,点E是边长为6的正方形所在平面内一动点,【问题思考】中其他条件不变,则动点P到边的最大距离为 (直接写出结果).
答案解析部分
1.【答案】线段的垂直平分线的性质
【解析】【解答】解:如图,连接 ,
∵点O为AC和BC的垂直平分线的交点,
∴OA=OC=OB,
∴⊙O为 的外接圆.
故答案为:线段的垂直平分线的性质.
【分析】利用线段垂直平分线的性质得到OA=OC=OB,然后根据点与圆的位置关系可判断点A、C在⊙O上.
2.【答案】2-2
【解析】【解答】解:∵四边形ABCD是正方形,
∴∠ABC=90°,
∴∠ABE+∠CBE=90°,
∵∠ABE=∠BCE,
∴∠BCE+∠CBE=90°,
∴∠BEC=90°,
∴点E在以BC为直径的半圆上移动,
如图,设BC的中点为O,作正方形ABCD关于直线AB对称的正方形APGB,则点D的对应点是P,
连接PO交AB于F,交半圆O于E,则线段EP的长即为FD+FE的长度最小值,OE=4,
∵∠G=90°,PG=BG=AB=4,
∴OG=6,
∴OP==,
∴EP=-2,
∴FD+FE的长度最小值为-2.
故答案为:2-2.
【分析】根据正方形的性质可得∠ABC=90°,由已知条件可得∠ABE=∠BCE,结合∠ABE+∠CBE=90°可得∠BEC=90°,则点E在以BC为直径的半圆上移动,设BC的中点为O,作正方形ABCD关于直线AB对称的正方形APGB,则点D的对应点是P,连接PO交AB于F,交半圆O于E,则线段EP的长即为FD+FE的长度最小值,OE=4,易得OG=6,利用勾股定理求出OP,进而可得EP,据此解答.
3.【答案】B
【解析】【解答】解:∵P为⊙O外一点,若点P到⊙O的最短距离为3,最长距离为7,
∴⊙O的直径为:7-3=4,
∴⊙O的半径为2,
故答案为:B.
【分析】由圆外一点到圆的最远距离与最近距离的差就是该圆的直径,即可算出答案。
4.【答案】B
【解析】【解答】解:点P在圆外,则点到圆心的距离大于圆的半径,
即: cm.
故答案为:B.
【分析】设点到圆心的距离为d,圆的半径为r,则 时,点在圆外;当 时,点在圆上;当 时,点在圆内.
5.【答案】B
【解析】【解答】解:不共线的三点确定一个圆,所以①错误;
在同圆或等圆中,相等的圆周角所对的弧相等,所以②错误;
同圆或等圆中,等弦所对的优弧或劣弧对应相等,所以③错误;
等边三角形的内心与外心重合,所以④正确;
三角形的外心到三角形各顶点的距离都相等,所以⑤正确.
故答案为:B.
【分析】根据确定圆的条件对①进行判断;根据圆周角定理对②进行判断;根据圆心角、弧、弦的关系对③进行判断;根据等边三角形的性质和三角形内心、外心的定义对④⑤进行判断.
6.【答案】C
【解析】【解答】解:∵圆O的半径为6cm,点P到圆心O的距离PO=8cm,6<8,
∴点P在圆O外,
故答案为:C.
【分析】设圆的半径为r,点到圆心的距离为d,当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内,据此判断即可得出答案.
7.【答案】A
【解析】【解答】解:如图所示:
点O为 外接圆圆心,则AO为外接圆半径,
故能够完全覆盖这个三角形的最小圆面的半径是: .
故答案为:A.
【分析】作出线段AB、AC的垂直平分线,其交点即为外接圆的圆心,结合勾股定理可求出圆的半径.
8.【答案】解:已知△ABC.
求证:∠A,∠B,∠C中不能有两个角是钝角.
证明:假设∠A,∠B,∠C中有两个角是钝角,不妨设∠A>90°,∠B>90°,
∴∠A+∠B+∠C>90°+90°+∠C>180°,这与“三角形内角和为180°”矛盾,
∴假设不成立,即在一个三角形中,不能有两个角是钝角。
【解析】【分析】根据反证法的证明方法,先假设∠A,∠B,∠C中有两个角是钝角,然后根据三角形内角和定理证明即可.
9.【答案】(1)解:作图如下图所示;
(2)以最长边为直径的圆
(3)解: 的外心(外接圆的圆心)
理由:如图, 的外接圆刚好覆盖E,F,H三点,与直线 交于点D,连接DH和DF
∵ ,
且 ,
∴ ,
∵∠HGF=50°+60°=110°,
∴ .
∴点G在点E,D之间.
即点G被外接圆覆盖,
此时该圆为能完全覆盖该四边形的最小圆.
因此,此基站应建在 的外心处.
【解析】【解答】解:(2)以最长边为直径的圆;
理由:∵线段 的最小覆盖圆就是以线段 为直径的圆,
由于∠A为钝角,因此∠A在圆内,
∴该圆为能完全覆盖该钝角三角形的最小圆.
【分析】(1)作出图1中任意两边的垂直平分线,其交点即为圆心,再以该点到三角形任意一个顶点之间的线段为半径画圆即可;作出图2中最长边的垂直平分线得到它的中点,再以中点为圆心,以这条最长边的一半长为半径作圆即可;
(2)依据最小覆盖圆的定义判断即可;
(3)先得到 的外接圆刚好覆盖E,F,H三点,再说明G点在圆内即可.
10.【答案】(1),
(2)解:问题思考中的结论仍然成立,理由如下:
设和交于点H,
∵四边形和四边形都为正方形,
∴,,
∴,
即,
∴,
∴,,
∵,
∴,
即,
∵,
∴,
即,
故答案为:,;
(3)
【解析】【解答】解:(1)设和交于点H,
∵四边形和四边形都为正方形,
∴,,
∴,
即,
∴,
∴,,
∵,
∴,
即,
∵,
∴,
即,
故答案为:,;
(3)∵,
∴点P的运用轨迹即为以为直径的上,
如图:
当点P位于右侧,且经过圆心O时,动点P到边的距离最大,
∵正方形的边长为,
∴,,
∴,
∴,
即动点P到边的最大距离为,
故答案为:.
【分析】【问题思考】设AQ和BC交于点H,由正方形的性质可得∠ADC=∠EDG=90°,DA=DC,DE=DG,根据角的和差关系可得∠ADE=∠CDG,利用SAS证明△DAE≌△DCG,得到AE=CG,∠DAE=∠DCG,根据等角的余角相等可得∠BAH=∠PCH,结合∠AHB=∠CHP可得∠B=∠CPA=90°,据此解答;
【问题类比】同上进行解答;
【拓展延伸】 由题意可得:点P的运用轨迹即为以AC为直径的⊙O上,当点P位于AD右侧,PH⊥AD且经过圆心O时,动点P到边AD的距离最大,由正方形的边长可得AC、OH、OP、PH的值,据此解答.
24.2.1 点和圆的位置关系一课一练
一、填空题
1.已知: ,求作 的外接圆,作法:①分别作线段BC,AC的垂直平分线EF和MN,它们交于点O;②以点O为圆心,OB的长为半径画弧,如图⊙O即为所求,以上作图用到的数学依据是 .
2.如图,已知正方形ABCD的边长为4,点E是正方形内部一点,连接BE,CE,且∠ABE=∠BCE,点F是AB边上一动点,连接FD,FE,则FD+FE的长度最小值为 .
二、单选题
3.设P为⊙O外一点,若点P到⊙O的最短距离为3,最长距离为7,则⊙O的半径为( )
A.3 B.2 C.4或10 D.2或5
4.已知⊙O的半径为3cm,且点P在⊙O外,则线段PO的长度为( )
A.等于6cm B.大于3cm C.小于3cm D.等于3cm
5.下列说法:①三点确定一个圆;②相等的圆周角所对的弧相等;③同圆或等圆中,等弦所对的弧相等;④等边三角形的内心与外心重合;⑤三角形的外心到三角形各顶点距离相等其中,正确的个数共有( )
A.1 B.2 C.3 D.4
6.若的半径为,点P到圆心O的距离,则点P的位置是( )
A.在内 B.在上 C.在外 D.不能确定
7.如图,将 放在每个小正方形边长为1的网格中,点A、B、C均落在格点上,用一个圆面去覆盖 ,能够完全覆盖这个三角形的最小圆面半径是
A. B. C.2 D.
三、解答题
8.求证:在一个三角形中,不能有两个角是钝角。
四、综合题
9.我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段 的最小覆盖圆就是以线段 为直径的圆.锐角三角形的最小覆盖圆是该三角形的外接圆.
(1)分别在图1,图2中作出 的最小覆盖圆.(要求尺规作图,保留作图痕迹,不写作法);
(2)根据(1)中的作图,钝角三角形的最小覆盖圆是 ;
(3)某地要修建一个 基站,服务四个村庄E、F、G、H(其位置如图3所示),为使信号可以覆盖四个村庄,且基站所需发射功率最小(距离越小,所需功率越小),此基站应建在何处?请说明理由.
五、实践探究题
10.
(1)【问题思考】
如图1,点E是正方形内的一点,过点E的直线,以为边向右侧作正方形,连接,直线与直线交于点P,则线段与之间的关系为 .
(2)【问题类比】
如图2,当点E是正方形外的一点时,【问题思考】中的结论还成立吗?若成立,请证明你的结论;若不成立,请说明理由;
(3)【拓展延伸】
如图3,点E是边长为6的正方形所在平面内一动点,【问题思考】中其他条件不变,则动点P到边的最大距离为 (直接写出结果).
答案解析部分
1.【答案】线段的垂直平分线的性质
【解析】【解答】解:如图,连接 ,
∵点O为AC和BC的垂直平分线的交点,
∴OA=OC=OB,
∴⊙O为 的外接圆.
故答案为:线段的垂直平分线的性质.
【分析】利用线段垂直平分线的性质得到OA=OC=OB,然后根据点与圆的位置关系可判断点A、C在⊙O上.
2.【答案】2-2
【解析】【解答】解:∵四边形ABCD是正方形,
∴∠ABC=90°,
∴∠ABE+∠CBE=90°,
∵∠ABE=∠BCE,
∴∠BCE+∠CBE=90°,
∴∠BEC=90°,
∴点E在以BC为直径的半圆上移动,
如图,设BC的中点为O,作正方形ABCD关于直线AB对称的正方形APGB,则点D的对应点是P,
连接PO交AB于F,交半圆O于E,则线段EP的长即为FD+FE的长度最小值,OE=4,
∵∠G=90°,PG=BG=AB=4,
∴OG=6,
∴OP==,
∴EP=-2,
∴FD+FE的长度最小值为-2.
故答案为:2-2.
【分析】根据正方形的性质可得∠ABC=90°,由已知条件可得∠ABE=∠BCE,结合∠ABE+∠CBE=90°可得∠BEC=90°,则点E在以BC为直径的半圆上移动,设BC的中点为O,作正方形ABCD关于直线AB对称的正方形APGB,则点D的对应点是P,连接PO交AB于F,交半圆O于E,则线段EP的长即为FD+FE的长度最小值,OE=4,易得OG=6,利用勾股定理求出OP,进而可得EP,据此解答.
3.【答案】B
【解析】【解答】解:∵P为⊙O外一点,若点P到⊙O的最短距离为3,最长距离为7,
∴⊙O的直径为:7-3=4,
∴⊙O的半径为2,
故答案为:B.
【分析】由圆外一点到圆的最远距离与最近距离的差就是该圆的直径,即可算出答案。
4.【答案】B
【解析】【解答】解:点P在圆外,则点到圆心的距离大于圆的半径,
即: cm.
故答案为:B.
【分析】设点到圆心的距离为d,圆的半径为r,则 时,点在圆外;当 时,点在圆上;当 时,点在圆内.
5.【答案】B
【解析】【解答】解:不共线的三点确定一个圆,所以①错误;
在同圆或等圆中,相等的圆周角所对的弧相等,所以②错误;
同圆或等圆中,等弦所对的优弧或劣弧对应相等,所以③错误;
等边三角形的内心与外心重合,所以④正确;
三角形的外心到三角形各顶点的距离都相等,所以⑤正确.
故答案为:B.
【分析】根据确定圆的条件对①进行判断;根据圆周角定理对②进行判断;根据圆心角、弧、弦的关系对③进行判断;根据等边三角形的性质和三角形内心、外心的定义对④⑤进行判断.
6.【答案】C
【解析】【解答】解:∵圆O的半径为6cm,点P到圆心O的距离PO=8cm,6<8,
∴点P在圆O外,
故答案为:C.
【分析】设圆的半径为r,点到圆心的距离为d,当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内,据此判断即可得出答案.
7.【答案】A
【解析】【解答】解:如图所示:
点O为 外接圆圆心,则AO为外接圆半径,
故能够完全覆盖这个三角形的最小圆面的半径是: .
故答案为:A.
【分析】作出线段AB、AC的垂直平分线,其交点即为外接圆的圆心,结合勾股定理可求出圆的半径.
8.【答案】解:已知△ABC.
求证:∠A,∠B,∠C中不能有两个角是钝角.
证明:假设∠A,∠B,∠C中有两个角是钝角,不妨设∠A>90°,∠B>90°,
∴∠A+∠B+∠C>90°+90°+∠C>180°,这与“三角形内角和为180°”矛盾,
∴假设不成立,即在一个三角形中,不能有两个角是钝角。
【解析】【分析】根据反证法的证明方法,先假设∠A,∠B,∠C中有两个角是钝角,然后根据三角形内角和定理证明即可.
9.【答案】(1)解:作图如下图所示;
(2)以最长边为直径的圆
(3)解: 的外心(外接圆的圆心)
理由:如图, 的外接圆刚好覆盖E,F,H三点,与直线 交于点D,连接DH和DF
∵ ,
且 ,
∴ ,
∵∠HGF=50°+60°=110°,
∴ .
∴点G在点E,D之间.
即点G被外接圆覆盖,
此时该圆为能完全覆盖该四边形的最小圆.
因此,此基站应建在 的外心处.
【解析】【解答】解:(2)以最长边为直径的圆;
理由:∵线段 的最小覆盖圆就是以线段 为直径的圆,
由于∠A为钝角,因此∠A在圆内,
∴该圆为能完全覆盖该钝角三角形的最小圆.
【分析】(1)作出图1中任意两边的垂直平分线,其交点即为圆心,再以该点到三角形任意一个顶点之间的线段为半径画圆即可;作出图2中最长边的垂直平分线得到它的中点,再以中点为圆心,以这条最长边的一半长为半径作圆即可;
(2)依据最小覆盖圆的定义判断即可;
(3)先得到 的外接圆刚好覆盖E,F,H三点,再说明G点在圆内即可.
10.【答案】(1),
(2)解:问题思考中的结论仍然成立,理由如下:
设和交于点H,
∵四边形和四边形都为正方形,
∴,,
∴,
即,
∴,
∴,,
∵,
∴,
即,
∵,
∴,
即,
故答案为:,;
(3)
【解析】【解答】解:(1)设和交于点H,
∵四边形和四边形都为正方形,
∴,,
∴,
即,
∴,
∴,,
∵,
∴,
即,
∵,
∴,
即,
故答案为:,;
(3)∵,
∴点P的运用轨迹即为以为直径的上,
如图:
当点P位于右侧,且经过圆心O时,动点P到边的距离最大,
∵正方形的边长为,
∴,,
∴,
∴,
即动点P到边的最大距离为,
故答案为:.
【分析】【问题思考】设AQ和BC交于点H,由正方形的性质可得∠ADC=∠EDG=90°,DA=DC,DE=DG,根据角的和差关系可得∠ADE=∠CDG,利用SAS证明△DAE≌△DCG,得到AE=CG,∠DAE=∠DCG,根据等角的余角相等可得∠BAH=∠PCH,结合∠AHB=∠CHP可得∠B=∠CPA=90°,据此解答;
【问题类比】同上进行解答;
【拓展延伸】 由题意可得:点P的运用轨迹即为以AC为直径的⊙O上,当点P位于AD右侧,PH⊥AD且经过圆心O时,动点P到边AD的距离最大,由正方形的边长可得AC、OH、OP、PH的值,据此解答.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
