24.2.2 直线和圆的位置关系一课一练(含解析)
文档属性
| 名称 | 24.2.2 直线和圆的位置关系一课一练(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 482.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-26 11:39:07 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
24.2.2 直线和圆的位置关系一课一练
一、填空题
1.直角三角形两直角边长为3和4,三角形内一点到各边距离相等,那么这个距离为 .
二、单选题
2. 的半径为5,圆心O到直线l的距离为3,则直线l与 的位置关系是
A.相交 B.相切 C.相离 D.无法确定
3.如图,以点 为圆心作圆恰好与直线 相切,则与半径相等的线段是( )
A. B. C. D.
4.到三角形三边的距离相等的点是( )
A.三角形三条高的交点 B.三角形三条中线的交点
C.三角形三条角平分线的交点 D.不存在这个点
5.如图所示, 是 的直径, 切 于点 ,线段 交 于点 ,连接 ,若 ,则 等于( ).
A.27° B.32° C.36° D.54°
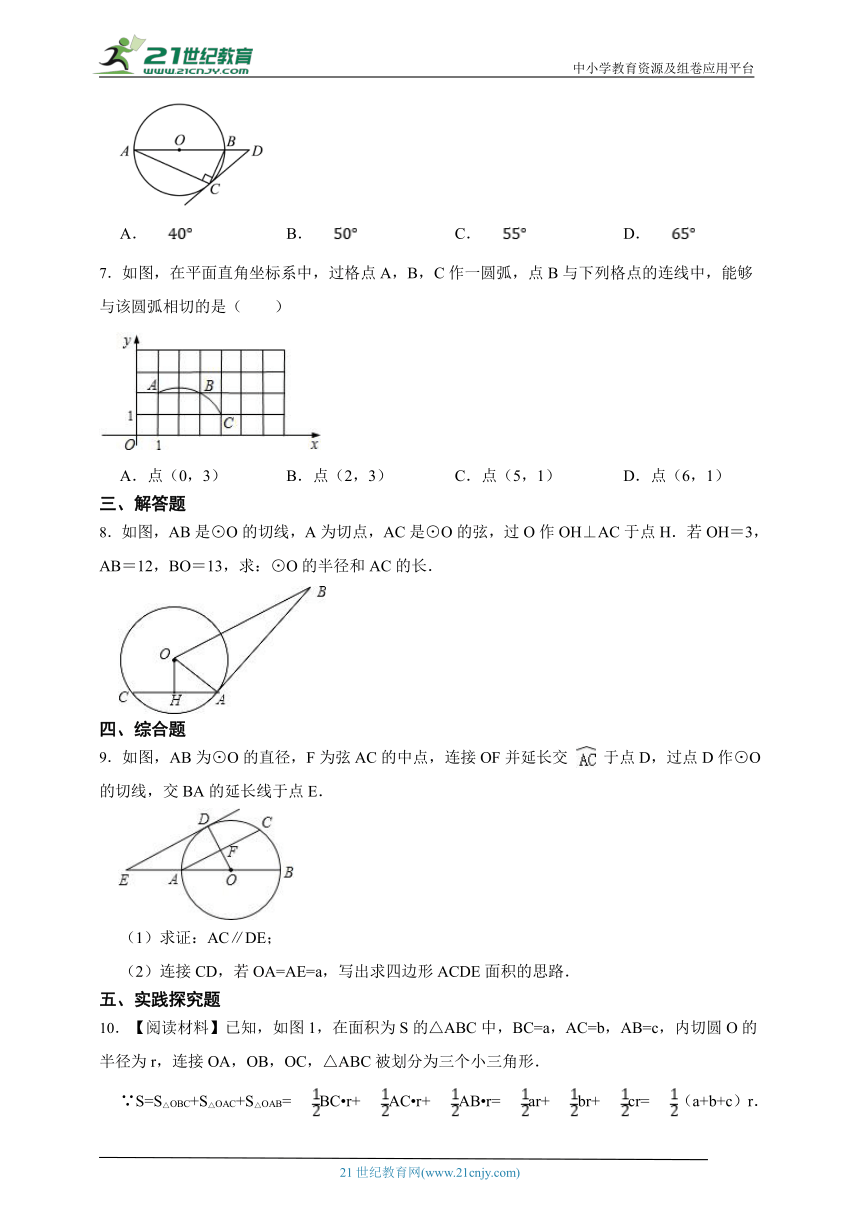
6.如图,圆O是的外接圆,,,过点C作圆O的切线,交的延长线于点D,则的度数是( )
A. B. C. D.
7.如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是( )
A.点(0,3) B.点(2,3) C.点(5,1) D.点(6,1)
三、解答题
8.如图,AB是⊙O的切线,A为切点,AC是⊙O的弦,过O作OH⊥AC于点H.若OH=3,AB=12,BO=13,求:⊙O的半径和AC的长.
四、综合题
9.如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交 于点D,过点D作⊙O的切线,交BA的延长线于点E.
(1)求证:AC∥DE;
(2)连接CD,若OA=AE=a,写出求四边形ACDE面积的思路.
五、实践探究题
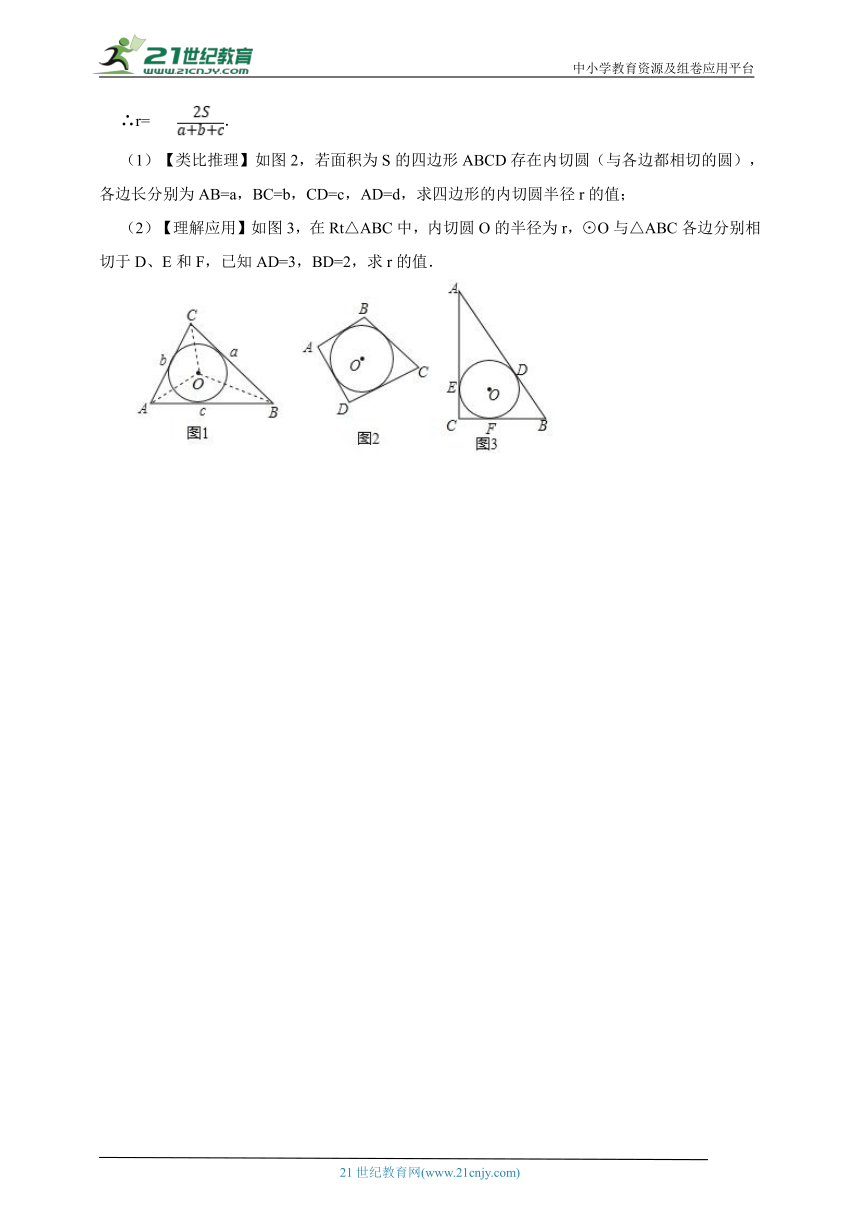
10.【阅读材料】已知,如图1,在面积为S的△ABC中,BC=a,AC=b,AB=c,内切圆O的半径为r,连接OA,OB,OC,△ABC被划分为三个小三角形.
∵S=S△OBC+S△OAC+S△OAB=BC r+AC r+AB r=ar+br+cr=(a+b+c)r.
∴r= .
(1)【类比推理】如图2,若面积为S的四边形ABCD存在内切圆(与各边都相切的圆),各边长分别为AB=a,BC=b,CD=c,AD=d,求四边形的内切圆半径r的值;
(2)【理解应用】如图3,在Rt△ABC中,内切圆O的半径为r,⊙O与△ABC各边分别相切于D、E和F,已知AD=3,BD=2,求r的值.
答案解析部分
1.【答案】1
【解析】【解答】解:连接OA,OB,OC,则点O到三边的距离就是△AOC,△BOC,△AOB的高线,设到三边的距离是x,则三个三角形的面积的和是:
AC x+ BC x+ AB x= AC BC,就可以得到x=1.
【分析】连接OA,OB,OC利用小三角形的面积和等于大三角形的面积即可解答.
2.【答案】A
【解析】【解答】∵⊙O的半径为5,圆心O到直线的距离为3,∴直线l与⊙O的位置关系是相交.
故答案为:A.
【分析】设⊙O的半径为r,圆心O到直线的距离为d,当d<r时,直线与⊙O相交;当d=r时,直线与⊙O相切,当d>r时,直线与⊙O相离,据此判断即可.
3.【答案】B
【解析】【解答】解:根据切线的性质可知圆的切线与过切点的半径互相垂直
∵
∴ PB是与圆半径相等的线段.
故答案为:B.
【分析】圆的切线与过切点的半径互相垂直,据此即可解答.
4.【答案】C
【解析】【解答】解:到三角形三边的距离相等的点是:三角形三条角平分线的交点.
故答案为:C.
【分析】三角形的内心:三个内角平分线的交点,它到三边的距离相等。
5.【答案】A
【解析】【解答】解:∵PA切 于点A,
∴ ,
∵ ,
∴ ,
∴ .
故答案为:A.
【分析】由切线的性质可得∠PAO=90°,结合题意由三角形的内角和定理可求得∠POA的度数,再根据圆周角定理可求解.
6.【答案】A
【解析】【解答】解:连接,
∵圆O是的外接圆,,
∴是直径,
∵,
∴,
∵是圆O的切线,
∴,
∴.
故答案为:A.
【分析】连接OC,利用圆周角定理可证得AB是直径,同时可求出∠BOC的度数;再利用切线的性质可证得∠OCD=90°,然后利用直角三角形的两锐角互余,可求出∠D的度数.
7.【答案】C
【解析】【解答】连接AC,作AC的垂直平分线BO′,交格点于点O′,则点O′AC就是所在圆的圆心,
∵过格点A,B,C作一圆弧,
∴三点组成的圆的圆心为:O(2,0),
∵只有∠OBD+∠EBF=90°时,BF与圆相切,
∴当△BO′D≌△FBE时,
∴EF=BD=2,
F点的坐标为:(5,1),
∴点B与下列格点的连线中,能够与该圆弧相切的是:(5,1).
故选:C.
【分析】根据垂径定理的性质得出圆心所在位置,再根据切线的性质得出,∠OBD+∠EBF=90°时F点的位置即可.此题主要考查了切线的性质以及垂径定理和坐标与图形的性质,得出△BOD≌△FBE时,EF=BD=2,即得出F点的坐标是解决问题的关键
8.【答案】解:∵AB为切线,
∴OA⊥AB,
∴∠OAB=90°,
在中,OA===5,
∵OH⊥AC,
∴AH=CH,
在中,AH===4,
∴AC=2AH=8,
答:⊙O的半径为5,AC的长为8.
【解析】【分析】由圆的切线的性质可得OA⊥AB,在Rt△OAB中,用勾股定理求得OA的值,由垂径定理可得AH=CH,在Rt△OAH中,用勾股定理求得AH的值,再根据垂径定理得AC=2AH可求解.
9.【答案】(1)证明:∵ED与⊙O相切于D,
∴OD⊥DE,
∵F为弦AC中点,
∴OD⊥AC,
∴AC∥DE.
(2)解:作DM⊥OA于M,连接CD,CO,AD.
首先证明四边形ACDE是平行四边形,根据S平行四边形ACDE=AE DM,只要求出DM即可.
∵AC∥DE,AE=AO,
∴OF=DF,
∵AF⊥DO,
∴AD=AO,
∴AD=AO=OD,
∴△ADO是等边三角形,同理△CDO也是等边三角形,
∴∠CDO=∠DOA=60°,AE=CD=AD=AO=DD=a,
∴AO∥CD,又AE=CD,
∴四边形ACDE是平行四边形,易知DM= a,
∴平行四边形ACDE面积= a2.
【解析】【分析】本题考查切线的性质、平行四边形的性质、垂径定理等知识,解题的关键是学会添加常用辅助线,利用特殊三角形解决问题,属于中考常考题型.(1)欲证明AC∥DE,只要证明AC⊥OD,ED⊥OD即可.(2)作DM⊥OA于M,连接CD,CO,AD,首先证明四边形ACDE是平行四边形,根据S平行四边形ACDE=AE DM,只要求出DM即可.
10.【答案】解:(1)如图2,连接OA、OB、OC、OD.∵S=S△AOB+S△BOC+S△COD+S△AOD=arbrcrdr=(a+b+c+d)r,∴r=;(2)如图3连接OE、OF,则四边形OECF是正方形,OE=EC=CF=FO=r,在Rt△ABC中,AC2+BC2=AB2,(3+r)2+(2+r)2=52,r2+5r﹣6=0,解得:r=1.
【解析】【分析】(1)已知已给出示例,我们仿照例子,连接OA,OB,OC,OD,则四边形被分为四个小三角形,且每个三角形都以内切圆半径为高,以四边形各边作底,这与题目情形类似.仿照证明过程,r易得.
(2)如图3,连接OE、OF,则四边形OECF是正方形,OE=EC=CF=FO=r,解直角三角形求得结果.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
24.2.2 直线和圆的位置关系一课一练
一、填空题
1.直角三角形两直角边长为3和4,三角形内一点到各边距离相等,那么这个距离为 .
二、单选题
2. 的半径为5,圆心O到直线l的距离为3,则直线l与 的位置关系是
A.相交 B.相切 C.相离 D.无法确定
3.如图,以点 为圆心作圆恰好与直线 相切,则与半径相等的线段是( )
A. B. C. D.
4.到三角形三边的距离相等的点是( )
A.三角形三条高的交点 B.三角形三条中线的交点
C.三角形三条角平分线的交点 D.不存在这个点
5.如图所示, 是 的直径, 切 于点 ,线段 交 于点 ,连接 ,若 ,则 等于( ).
A.27° B.32° C.36° D.54°
6.如图,圆O是的外接圆,,,过点C作圆O的切线,交的延长线于点D,则的度数是( )
A. B. C. D.
7.如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是( )
A.点(0,3) B.点(2,3) C.点(5,1) D.点(6,1)
三、解答题
8.如图,AB是⊙O的切线,A为切点,AC是⊙O的弦,过O作OH⊥AC于点H.若OH=3,AB=12,BO=13,求:⊙O的半径和AC的长.
四、综合题
9.如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交 于点D,过点D作⊙O的切线,交BA的延长线于点E.
(1)求证:AC∥DE;
(2)连接CD,若OA=AE=a,写出求四边形ACDE面积的思路.
五、实践探究题
10.【阅读材料】已知,如图1,在面积为S的△ABC中,BC=a,AC=b,AB=c,内切圆O的半径为r,连接OA,OB,OC,△ABC被划分为三个小三角形.
∵S=S△OBC+S△OAC+S△OAB=BC r+AC r+AB r=ar+br+cr=(a+b+c)r.
∴r= .
(1)【类比推理】如图2,若面积为S的四边形ABCD存在内切圆(与各边都相切的圆),各边长分别为AB=a,BC=b,CD=c,AD=d,求四边形的内切圆半径r的值;
(2)【理解应用】如图3,在Rt△ABC中,内切圆O的半径为r,⊙O与△ABC各边分别相切于D、E和F,已知AD=3,BD=2,求r的值.
答案解析部分
1.【答案】1
【解析】【解答】解:连接OA,OB,OC,则点O到三边的距离就是△AOC,△BOC,△AOB的高线,设到三边的距离是x,则三个三角形的面积的和是:
AC x+ BC x+ AB x= AC BC,就可以得到x=1.
【分析】连接OA,OB,OC利用小三角形的面积和等于大三角形的面积即可解答.
2.【答案】A
【解析】【解答】∵⊙O的半径为5,圆心O到直线的距离为3,∴直线l与⊙O的位置关系是相交.
故答案为:A.
【分析】设⊙O的半径为r,圆心O到直线的距离为d,当d<r时,直线与⊙O相交;当d=r时,直线与⊙O相切,当d>r时,直线与⊙O相离,据此判断即可.
3.【答案】B
【解析】【解答】解:根据切线的性质可知圆的切线与过切点的半径互相垂直
∵
∴ PB是与圆半径相等的线段.
故答案为:B.
【分析】圆的切线与过切点的半径互相垂直,据此即可解答.
4.【答案】C
【解析】【解答】解:到三角形三边的距离相等的点是:三角形三条角平分线的交点.
故答案为:C.
【分析】三角形的内心:三个内角平分线的交点,它到三边的距离相等。
5.【答案】A
【解析】【解答】解:∵PA切 于点A,
∴ ,
∵ ,
∴ ,
∴ .
故答案为:A.
【分析】由切线的性质可得∠PAO=90°,结合题意由三角形的内角和定理可求得∠POA的度数,再根据圆周角定理可求解.
6.【答案】A
【解析】【解答】解:连接,
∵圆O是的外接圆,,
∴是直径,
∵,
∴,
∵是圆O的切线,
∴,
∴.
故答案为:A.
【分析】连接OC,利用圆周角定理可证得AB是直径,同时可求出∠BOC的度数;再利用切线的性质可证得∠OCD=90°,然后利用直角三角形的两锐角互余,可求出∠D的度数.
7.【答案】C
【解析】【解答】连接AC,作AC的垂直平分线BO′,交格点于点O′,则点O′AC就是所在圆的圆心,
∵过格点A,B,C作一圆弧,
∴三点组成的圆的圆心为:O(2,0),
∵只有∠OBD+∠EBF=90°时,BF与圆相切,
∴当△BO′D≌△FBE时,
∴EF=BD=2,
F点的坐标为:(5,1),
∴点B与下列格点的连线中,能够与该圆弧相切的是:(5,1).
故选:C.
【分析】根据垂径定理的性质得出圆心所在位置,再根据切线的性质得出,∠OBD+∠EBF=90°时F点的位置即可.此题主要考查了切线的性质以及垂径定理和坐标与图形的性质,得出△BOD≌△FBE时,EF=BD=2,即得出F点的坐标是解决问题的关键
8.【答案】解:∵AB为切线,
∴OA⊥AB,
∴∠OAB=90°,
在中,OA===5,
∵OH⊥AC,
∴AH=CH,
在中,AH===4,
∴AC=2AH=8,
答:⊙O的半径为5,AC的长为8.
【解析】【分析】由圆的切线的性质可得OA⊥AB,在Rt△OAB中,用勾股定理求得OA的值,由垂径定理可得AH=CH,在Rt△OAH中,用勾股定理求得AH的值,再根据垂径定理得AC=2AH可求解.
9.【答案】(1)证明:∵ED与⊙O相切于D,
∴OD⊥DE,
∵F为弦AC中点,
∴OD⊥AC,
∴AC∥DE.
(2)解:作DM⊥OA于M,连接CD,CO,AD.
首先证明四边形ACDE是平行四边形,根据S平行四边形ACDE=AE DM,只要求出DM即可.
∵AC∥DE,AE=AO,
∴OF=DF,
∵AF⊥DO,
∴AD=AO,
∴AD=AO=OD,
∴△ADO是等边三角形,同理△CDO也是等边三角形,
∴∠CDO=∠DOA=60°,AE=CD=AD=AO=DD=a,
∴AO∥CD,又AE=CD,
∴四边形ACDE是平行四边形,易知DM= a,
∴平行四边形ACDE面积= a2.
【解析】【分析】本题考查切线的性质、平行四边形的性质、垂径定理等知识,解题的关键是学会添加常用辅助线,利用特殊三角形解决问题,属于中考常考题型.(1)欲证明AC∥DE,只要证明AC⊥OD,ED⊥OD即可.(2)作DM⊥OA于M,连接CD,CO,AD,首先证明四边形ACDE是平行四边形,根据S平行四边形ACDE=AE DM,只要求出DM即可.
10.【答案】解:(1)如图2,连接OA、OB、OC、OD.∵S=S△AOB+S△BOC+S△COD+S△AOD=arbrcrdr=(a+b+c+d)r,∴r=;(2)如图3连接OE、OF,则四边形OECF是正方形,OE=EC=CF=FO=r,在Rt△ABC中,AC2+BC2=AB2,(3+r)2+(2+r)2=52,r2+5r﹣6=0,解得:r=1.
【解析】【分析】(1)已知已给出示例,我们仿照例子,连接OA,OB,OC,OD,则四边形被分为四个小三角形,且每个三角形都以内切圆半径为高,以四边形各边作底,这与题目情形类似.仿照证明过程,r易得.
(2)如图3,连接OE、OF,则四边形OECF是正方形,OE=EC=CF=FO=r,解直角三角形求得结果.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
