3.2简单的三角恒等变换2
图片预览






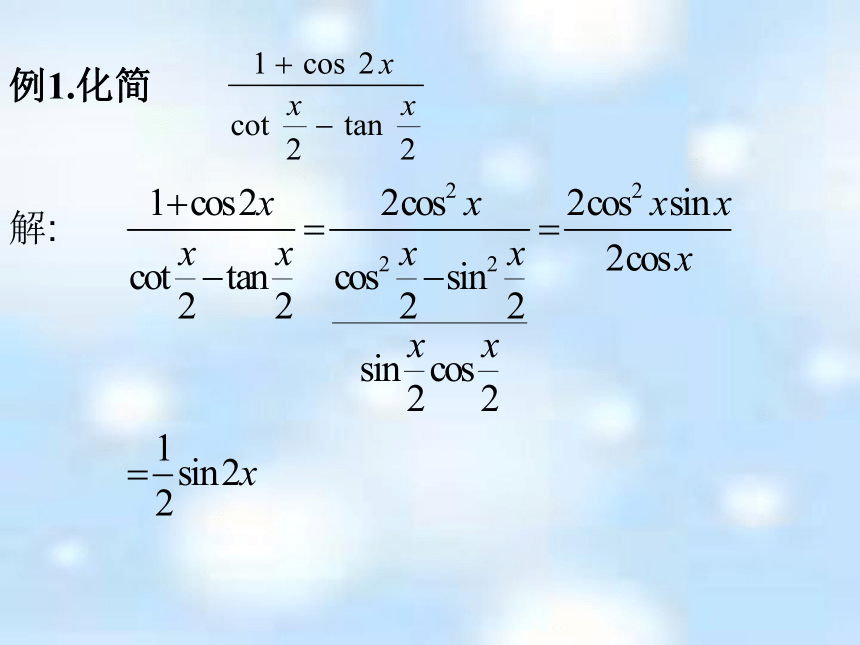

文档简介
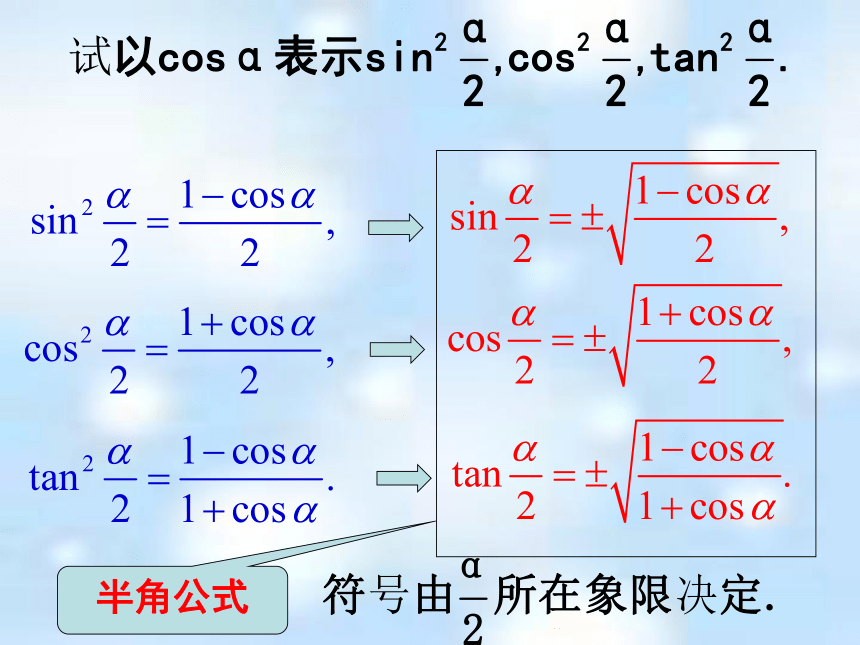
课件21张PPT。3.2 简单的三角恒等变换学习目标:1.利用已有的公式进行简单的恒等变换 2.三角恒等变换在数学中的应用. 复习十一个公式:cosαcosβ+sinαsinβcosαcosβ-sinαsinβsinαcosβ+cosαsinβsinαcosβ-cosαsinβsin2α=____________ (S2α)cos2α=____________ (C2α)2sinαcosαcos2α- sin2α 2cos2α- 1 1- 2sin2α cos2α=____________ cos2α=____________ 半角公式半角公式 思考:代数式变换与三角变换有什么不同?
代数式变换往往着眼于式子结构形式的变换.对于三角变换,由于不同的三角函数式不仅会有结构形式方面的差异,而且还会有所包含的角,以及这些角的三角函数种类方面的差异,因此三角恒等变换常常首先寻找式子所包含的各个角之间的联系,这是三角式恒等变换的重要特点.例1.化简解:例2.化简:解法1:解法2: 解法3:解法4:练习1.已知函数f(x)=log (sinx-cosx)
(1)求它的定义域与值域
(2)求它的单调区间
(3)判断奇偶性
(4)判断它的周期性,如果是周期函数,求出它的最小正周期
小结:对公式我们不仅要会直接的运用,还要会逆用、还要会变形用,还要会与其它的公式一起灵活的运用。 三角函数中有许多恒等关系,这些关系大体上可分为三类。
第一类是三角函数本身蕴涵的恒等关系。如,对于正弦函数,有sinx =sin(x+ 2k ),sin( - x)= - sinx, sin(2- x)= - sinx, sin(-x)=sinx, sin(+x)=- sinx, 等诱导公式。
这些恒等关系反映了正弦函数的周期性、
奇偶性等性质。
第二类是边角关系中蕴涵的恒等关系。如, ,,这些恒等关系反映了边角之间的联系以
及同角的不同三角函数之间的联系。
第三类是三角函数运算中蕴涵的恒等关系。如, , 等,这些恒等关系映了
sinx ,cosx ,siny, cosy 与sin(x +y)、cos(x+y)之间的联系。作业:
代数式变换往往着眼于式子结构形式的变换.对于三角变换,由于不同的三角函数式不仅会有结构形式方面的差异,而且还会有所包含的角,以及这些角的三角函数种类方面的差异,因此三角恒等变换常常首先寻找式子所包含的各个角之间的联系,这是三角式恒等变换的重要特点.例1.化简解:例2.化简:解法1:解法2: 解法3:解法4:练习1.已知函数f(x)=log (sinx-cosx)
(1)求它的定义域与值域
(2)求它的单调区间
(3)判断奇偶性
(4)判断它的周期性,如果是周期函数,求出它的最小正周期
小结:对公式我们不仅要会直接的运用,还要会逆用、还要会变形用,还要会与其它的公式一起灵活的运用。 三角函数中有许多恒等关系,这些关系大体上可分为三类。
第一类是三角函数本身蕴涵的恒等关系。如,对于正弦函数,有sinx =sin(x+ 2k ),sin( - x)= - sinx, sin(2- x)= - sinx, sin(-x)=sinx, sin(+x)=- sinx, 等诱导公式。
这些恒等关系反映了正弦函数的周期性、
奇偶性等性质。
第二类是边角关系中蕴涵的恒等关系。如, ,,这些恒等关系反映了边角之间的联系以
及同角的不同三角函数之间的联系。
第三类是三角函数运算中蕴涵的恒等关系。如, , 等,这些恒等关系映了
sinx ,cosx ,siny, cosy 与sin(x +y)、cos(x+y)之间的联系。作业:
