1.4.2用空间向量研究距离、夹角问题(第1课时) 课件(共31张PPT)
文档属性
| 名称 | 1.4.2用空间向量研究距离、夹角问题(第1课时) 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-24 00:00:00 | ||
图片预览






文档简介
(共31张PPT)
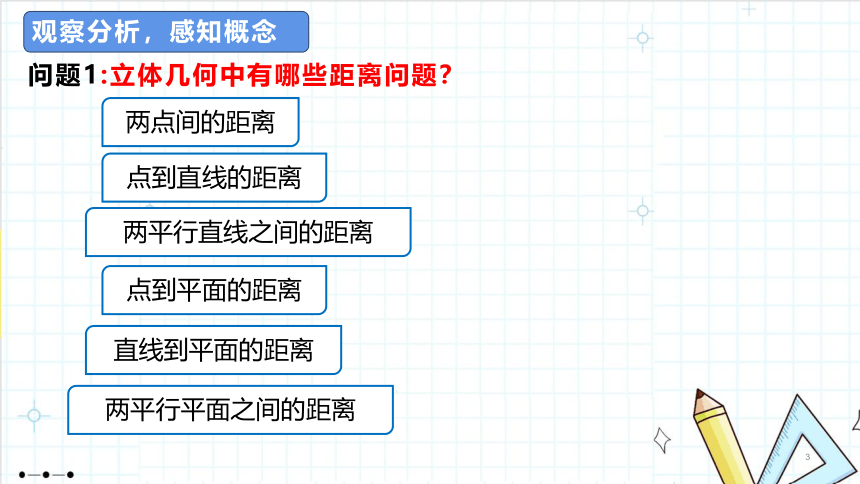
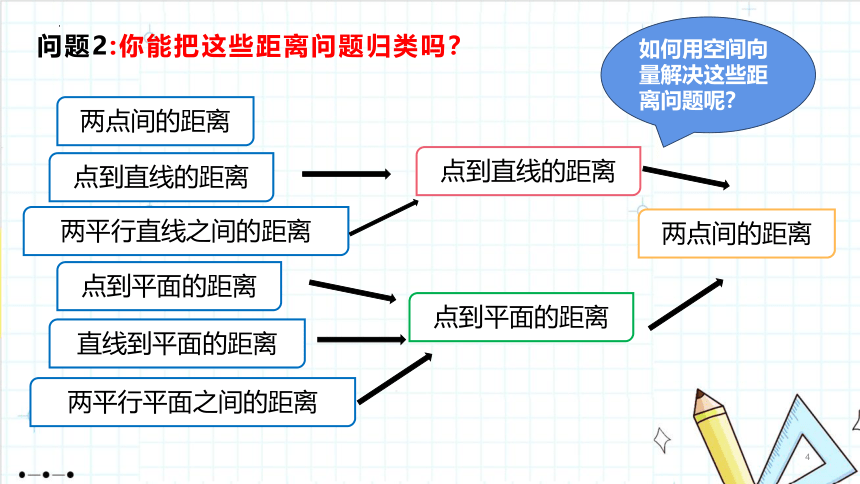
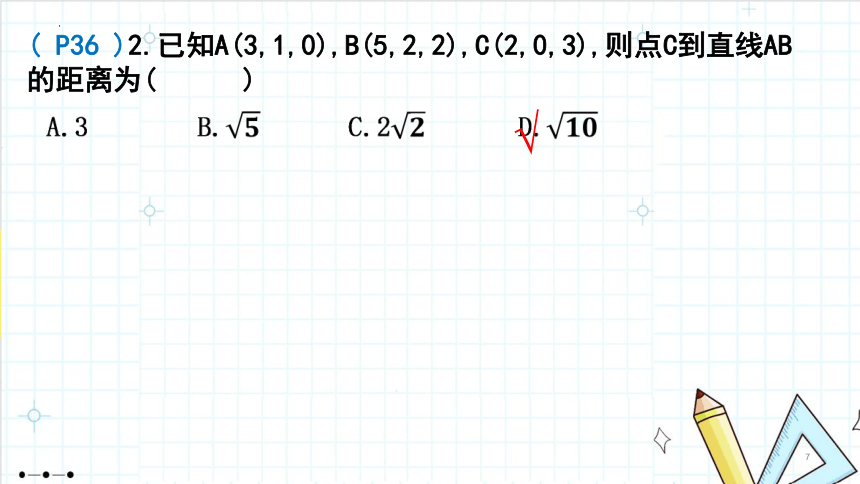
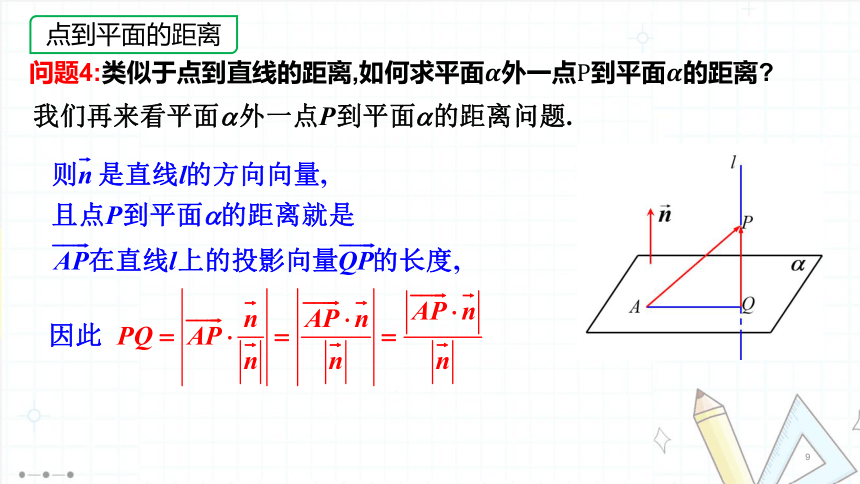
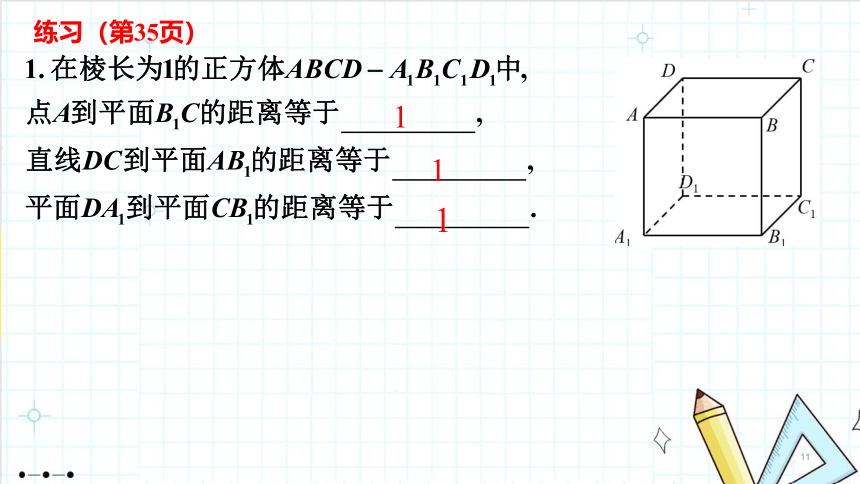
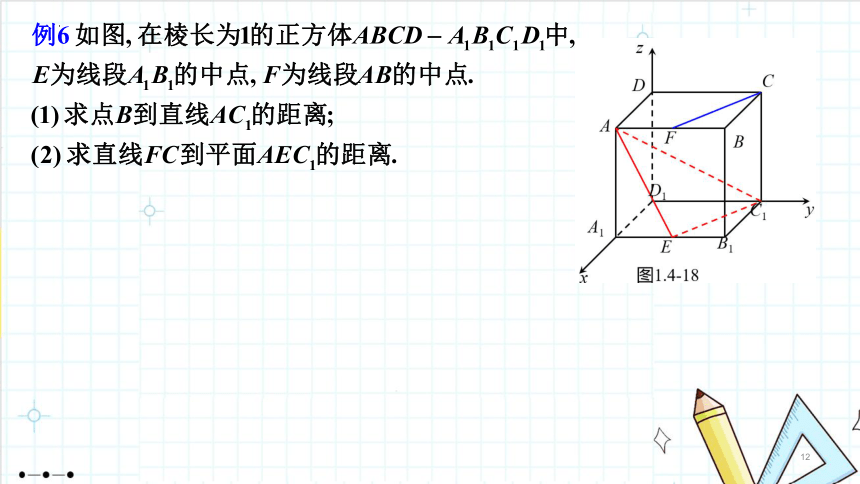
1.4.2用空间向量研究距离、夹角问题(第1课时)如图,有一条笔直的公路,某人要在点A处,修建一个蔬菜存储库。在公路上选择一个点,修一条公路到达A点,要想使这个路线长度理论上最短,应该如何设计?创设情境,引入课题问题1:立体几何中有哪些距离问题?观察分析,感知概念两点间的距离点到直线的距离两平行直线之间的距离两平行平面之间的距离点到平面的距离直线到平面的距离问题2:你能把这些距离问题归类吗?两点间的距离点到直线的距离两平行直线之间的距离两平行平面之间的距离点到平面的距离直线到平面的距离点到直线的距离点到平面的距离两点间的距离如何用空间向量解决这些距离问题呢?问题3:己知一条直线和直线外一点求点到直线的距离.APQl点到直线的距离P33[做一做1]已知直线过点且方向向量为,则点到的距离为( )√( P36 )2.已知A(3,1,0),B(5,2,2),C(2,0,3),则点C到直线AB的距离为( )√思考:类比点到直线的距离的求法,如何求两条平行直线之间的距离?问题4:类似于点到直线的距离,如何求平面外一点到平面的距离 点到平面的距离P33[做一做2]已知为平面的一个法向量,为内的一点,则点到平面的距离为( )√练习(第35页)111ACBDyxzA1B1C1D1EF图1.4-18利用向量法求点到平面的距离的一般步骤(1)建立空间直角坐标系.(2)求出该平面的一个法向量.(3)找出该点与平面内一点连线形成的斜线段对应的向量.(4)法向量与斜线段对应向量的数量积的绝对值再除以法向量的模,即为点到平面的距离.ACBDA1B1C1D1xyzACBDA1B1C1D1xyzACBDA1B1C1D1与用平面向量解决平面几何问题的“三步曲”类似,我们可以得出用空间向量解决立体几何问题的“三步曲”:(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间的距离和夹角等问题;(3)把向量运算的结果“翻译”成相应的几何结论.问题7:回顾这节课的学习,我们学习了哪些内容 用的是什么方法 1.知识总结:2.用空间向量解决立体几何问题的“三步曲”归纳总结,反思提升例3已知在棱长为1的正方体中,为线段的中点,为线段的中点.(1)若的中点为,求直线与直线的距离;(2)求平面与平面的距离.例3已知在棱长为1的正方体中,为线段的中点,为线段的中点.(2)求两个平行平面间的距离可以转化为求点到平面的距离,利用求点到平面的距离的方法求解即可.(1)求线面距离可以转化为求直线上任意一点到平面的距离,利用求点到平面的距离的方法求解即可.例2如图,在正四棱柱中,已知分别为上的点,且.(1)求证:平面;(2)求点到平面的距离.√ACBDA1B1C1D1EFxyzACBDA1B1C1D1EFxyzACBDA1B1C1D1EFxyzACBDA1B1C1D1EFxyzACBDA1B1C1D1EFxyz
1.4.2用空间向量研究距离、夹角问题(第1课时)如图,有一条笔直的公路,某人要在点A处,修建一个蔬菜存储库。在公路上选择一个点,修一条公路到达A点,要想使这个路线长度理论上最短,应该如何设计?创设情境,引入课题问题1:立体几何中有哪些距离问题?观察分析,感知概念两点间的距离点到直线的距离两平行直线之间的距离两平行平面之间的距离点到平面的距离直线到平面的距离问题2:你能把这些距离问题归类吗?两点间的距离点到直线的距离两平行直线之间的距离两平行平面之间的距离点到平面的距离直线到平面的距离点到直线的距离点到平面的距离两点间的距离如何用空间向量解决这些距离问题呢?问题3:己知一条直线和直线外一点求点到直线的距离.APQl点到直线的距离P33[做一做1]已知直线过点且方向向量为,则点到的距离为( )√( P36 )2.已知A(3,1,0),B(5,2,2),C(2,0,3),则点C到直线AB的距离为( )√思考:类比点到直线的距离的求法,如何求两条平行直线之间的距离?问题4:类似于点到直线的距离,如何求平面外一点到平面的距离 点到平面的距离P33[做一做2]已知为平面的一个法向量,为内的一点,则点到平面的距离为( )√练习(第35页)111ACBDyxzA1B1C1D1EF图1.4-18利用向量法求点到平面的距离的一般步骤(1)建立空间直角坐标系.(2)求出该平面的一个法向量.(3)找出该点与平面内一点连线形成的斜线段对应的向量.(4)法向量与斜线段对应向量的数量积的绝对值再除以法向量的模,即为点到平面的距离.ACBDA1B1C1D1xyzACBDA1B1C1D1xyzACBDA1B1C1D1与用平面向量解决平面几何问题的“三步曲”类似,我们可以得出用空间向量解决立体几何问题的“三步曲”:(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间的距离和夹角等问题;(3)把向量运算的结果“翻译”成相应的几何结论.问题7:回顾这节课的学习,我们学习了哪些内容 用的是什么方法 1.知识总结:2.用空间向量解决立体几何问题的“三步曲”归纳总结,反思提升例3已知在棱长为1的正方体中,为线段的中点,为线段的中点.(1)若的中点为,求直线与直线的距离;(2)求平面与平面的距离.例3已知在棱长为1的正方体中,为线段的中点,为线段的中点.(2)求两个平行平面间的距离可以转化为求点到平面的距离,利用求点到平面的距离的方法求解即可.(1)求线面距离可以转化为求直线上任意一点到平面的距离,利用求点到平面的距离的方法求解即可.例2如图,在正四棱柱中,已知分别为上的点,且.(1)求证:平面;(2)求点到平面的距离.√ACBDA1B1C1D1EFxyzACBDA1B1C1D1EFxyzACBDA1B1C1D1EFxyzACBDA1B1C1D1EFxyzACBDA1B1C1D1EFxyz
