第四章 几何图形初步 素养综合检测(含答案)
文档属性
| 名称 | 第四章 几何图形初步 素养综合检测(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 290.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-25 11:11:41 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024人教版数学七年级上学期同步练习
第四章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共30分)
1.【新独家原创】同学们用过下图这种折扇吧 因为它折起来便于携带,所以受到人们的喜爱.折扇展开的过程运用了数学上的 原理. ( )
A.点动成线
B.线动成面
C.面动成体
D.面与面相交的地方是线
2.(2022湖北随州中考)如图所示的是一个放在水平桌面上的半球体,该几何体从不同的方向看到的图形完全相同的是 ( )
A.从正面看和从左面看
B.从正面看和从上面看
C.从左面看和从上面看
D.从各个方向看
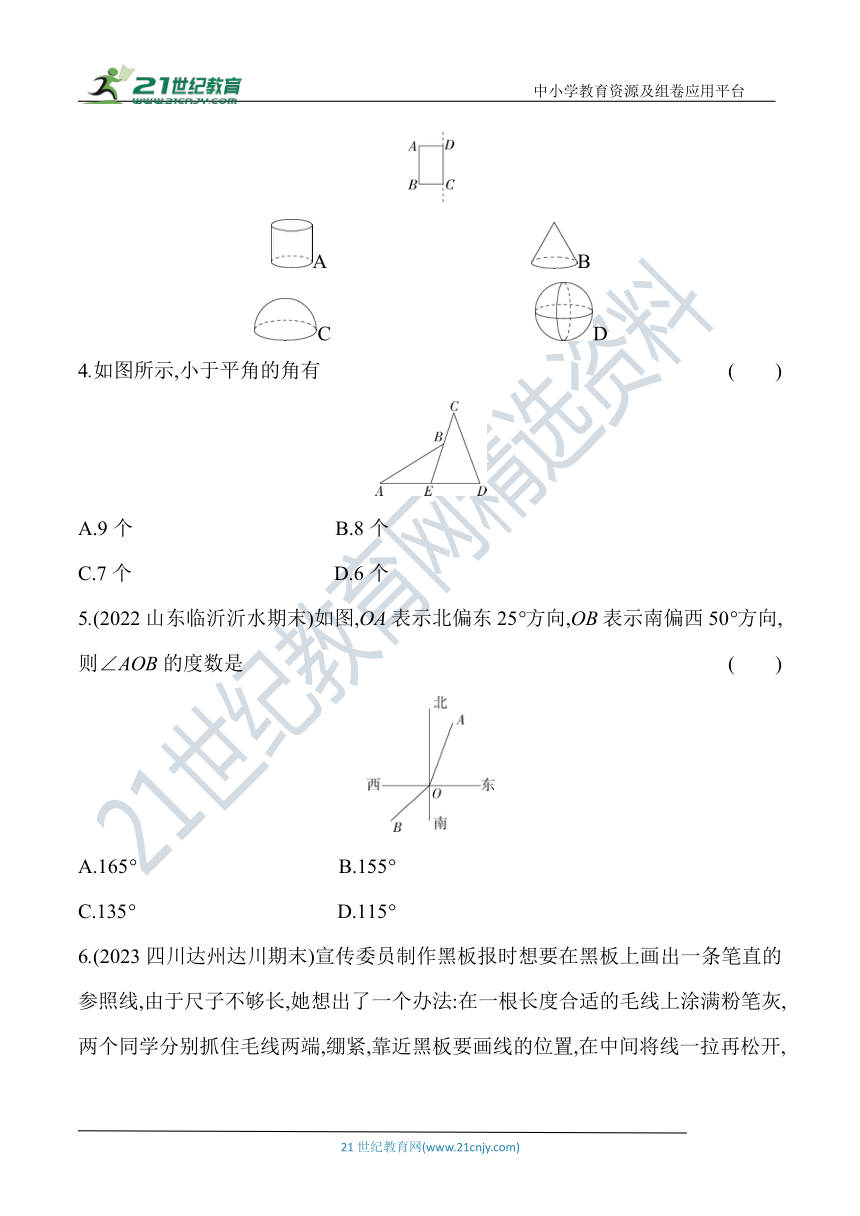
3.(2022四川自贡中考)如图,将长方形纸片ABCD绕边CD所在直线旋转一周,得到的立体图形是 ( )
A B
C D
4.如图所示,小于平角的角有 ( )
A.9个 B.8个
C.7个 D.6个
5.(2022山东临沂沂水期末)如图,OA表示北偏东25°方向,OB表示南偏西50°方向,则∠AOB的度数是 ( )
A.165° B.155°
C.135° D.115°
6.(2023四川达州达川期末)宣传委员制作黑板报时想要在黑板上画出一条笔直的参照线,由于尺子不够长,她想出了一个办法:在一根长度合适的毛线上涂满粉笔灰,两个同学分别抓住毛线两端,绷紧,靠近黑板要画线的位置,在中间将线一拉再松开,毛线弹回到黑板上,这样黑板上就出现了一条笔直的“粉笔灰线”,这种画法的数学依据是 ( )
A.两点之间,线段最短
B.两点确定一条直线
C.线段的中点的定义
D.两点间的距离的定义
7.(2023湖南郴州汝城校级期末)如图,若∠AOB>∠COD,则∠AOD与∠BOC的大小关系是 ( )
A.∠AOD=∠BOC
B.∠AOD<∠BOC
C.∠AOD>∠BOC
D.不能确定
8.(2022江苏泰州中考)如图所示的是一个几何体的展开图,则该几何体是 ( )
A.三棱锥 B.四棱锥
C.四棱柱 D.圆锥
9.射线OA上有B、C两点,若OB=8,BC=2,线段OB、BC的中点分别为D、E,则线段DE的长为 ( )
A.5 B.1或3
C.1 D.5或3
10.(2023辽宁沈阳铁西期末)每天中午11点30分“校园之声”节目都会如约而至,11点30分时时针与分针所夹的角为 ( )
A.170° B.175° C.165° D.160°
二、填空题(每小题3分,共30分)
11.(2022浙江杭州模拟)子弹从枪膛中射出去的轨迹可看成一条线,这说明 的数学道理.
12.已知线段AB=6 cm,延长线段AB到C,使BC=AB,反向延长线段AB到D,使AD=AC,则线段CD的长为 .
13.(2022山东济南历下期末)计算:30°12'= °.
14.【新情境·全向十字路口】(2023北京石景山期末)北京首个全向十字路口设于石景山区,为行人带来了很多便利.从上面看得到的平面图形如图所示.若想走近路,从位置A到位置C的两条路径“A→C”和“A→B→C”中选,你会选择路径 ,选择的依据是 .
15.(2022北京通州期末)如图,棋盘上有黑、白两色棋子若干,若直线l经过3枚颜色相同的棋子,则这样的直线共有 条.
16.【跨学科·生物】(2023吉林长春双阳期末)大自然中存在着许多奇妙的现象,科学家通过观察惊奇地发现,植物的茎叶和果实几乎都是按照137°30'的模式排列的.这样,植物的茎叶和果实就可以占有最大的空间,以获取最多的阳光,承接最多的雨水.以上描述中的137°30'的补角是 °.
17.(2022天津北辰期末)如图,辰辰同学根据这个图形写出了四个结论:①图中有两条直线;②图中有5条线段;③射线AC和射线AD是同一条射线;④直线BD经过点C.其中正确的结论是 .(填序号)
18.(2021湖北黄冈期末)如图,将一副直角三角板叠放在一起,使直角顶点重合于点O,则∠AOB+∠DOC= 度.
19.(2023山东菏泽曹县期末)如图,点C,D在线段AB上,且AC=CD=DB,点E是线段DB的中点,若CE=12 cm,则AB的长为 .
20.(2022安徽合肥蜀山期末)在同一平面内,∠AOC=∠BOD=50°,射线OB在∠AOC的内部,且∠AOB=20°,OE平分∠AOD,则∠COE的度数是 .
三、解答题(共40分)
21.(5分)如图,已知不在同一直线上的四个点A、B、C、D.
(1)画直线AD;
(2)连接AB;
(3)画射线CD;
(4)延长线段BA至点E,使BE=2BA;
(5)反向延长射线CD至点F,使DC=2CF.
22.(2022北京东城期末)(5分)若一个角的补角是它的余角的6倍,求这个角的度数.
23.(2023北京昌平期末)(6分)如图,C,D,E是线段AB上的点,AC=5,BD=3,点C,E分别是线段AD,BD的中点,求CE的长.
24.(2022广西玉林博白期末)(8分)如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.
(1)射线OC的方向是 ;
(2)若射线OE平分∠COD,求∠AOE的度数.
25.(8分)如图,数轴上点A,B表示的有理数分别为-6,3,若点P是射线AB上一个动点(不与点A,B重合),M是线段AP上靠近点A的三等分点,N是线段BP上靠近点B的三等分点.
(1)当点P表示的有理数是0时,MN的长为 ,当点P表示的有理数是6时,MN的长为 ;
(2)点P在射线AB上运动(不与点A,B重合)的过程中,MN的长是否发生改变 若不改变,请写出求MN的长的过程;若改变,请说明理由.
26.(8分)点O为直线AB上一点,将一直角三角板OMN的直角顶点放在点O处,射线OC平分∠BOM.
(1)如图1,若∠AOM=30°,求∠CON的度数;
(2)在图1中,若∠AOM=α,直接写出∠CON的度数(用含α的式子表示);
(3)将图1中的直角三角板OMN绕点O顺时针旋转至图2的位置,一边OM在直线AB上方,另一边ON在直线AB下方.
①探究∠AOM和∠CON的度数之间的关系,写出你的结论,并说明理由;
②当∠AOC=3∠BON时,求∠AOM的度数.
图1 图2
答案全解全析
一、选择题
1.B 开始的状态可以看成线,结束的状态可以看成面,所以运用了线动成面的原理.
2.A 该几何体从正面看和从左面看均为半圆,故选A.
3.A 将长方形纸片ABCD绕边CD所在直线旋转一周,可知旋转后有两个平的面,所以得到的立体图形是圆柱体.
4.C 符合条件的角中,以A为顶点的角有1个,以B为顶点的角有2个,以C为顶点的角有1个,以D为顶点的角有1个,以E为顶点的角有2个,共有1+2+1+1+2=7个,故选C.
5.B 由题意得∠AOB=25°+90°+(90°-50°)=155°.
6.B 这种画法的数学依据是两点确定一条直线.故选B.
7.C 因为∠AOB>∠COD,∠AOD=∠AOB+∠BOD,∠BOC=∠COD+∠BOD,
所以∠AOD>∠BOC.
8.B 根据展开图可以得出该几何体是四棱锥,故选B.
9.D 因为OB=8,D是OB的中点,
所以DB=4,
因为BC=2,E是BC的中点,
所以BE=1.
如图1,DE=BD-BE=3;
如图2,DE=BD+BE=5.故选D.
图1
图2
10.C 6×30°-×30°=180°-15°=165°,
所以时针与分针所夹的角为165°.故选C.
二、填空题
11.点动成线
12.18 cm
解析 AC=AB+BC=6+×6=9(cm),则CD=AD+AC=2AC=2×9=18(cm).
13.30.2
解析 因为1°=60',所以12'=0.2°,所以30°12'=30.2°.
14.A→C;两点之间,线段最短
15.3
解析 如图所示:
所以满足条件的直线共有3条.
16.42.5
解析 180°-137°30'=42°30'=42.5°.
17.①③
解析 题图中有两条直线:直线BD,直线BC;
题图中有6条线段:线段AB,线段BC,线段BD,线段AC,线段CD,线段AD;射线AC和射线AD的端点和方向都相同,是同一条射线;直线BD不经过点C.
故正确的结论是①③.
18.180
解析 ∠AOB+∠DOC=∠AOD+∠DOC+∠BOC+∠DOC=∠AOC+∠DOB=90°+90°=180°.
19.24 cm
解析 因为AC=CD=DB,点E是线段DB的中点,
所以AB=AD+DB=(AC+CD)+(DE+BE)=2(CD+DE)=2CE=24 cm.
20.15°或65°
解析 ①当OD与OC在OA的同侧时,
如图,
因为∠AOC=∠BOD=50°,∠AOB=20°,
所以∠AOD=∠BOD+∠AOB=70°,
因为OE平分∠AOD,
所以∠AOE=∠AOD=35°,
所以∠COE=∠AOC-∠AOE=15°;
②当OD与OC在OA的异侧时,
如图,
因为∠AOC=∠BOD=50°,∠AOB=20°,
所以∠AOD=∠BOD-∠AOB=30°,
因为OE平分∠AOD,
所以∠AOE=∠AOD=15°,
所以∠COE=∠AOC+∠AOE=65°.
综上所述,∠COE的度数为15°或65°.
三、解答题
21.解析 (1)(2)(3)(4)(5)如图所示.
22.解析 设这个角的度数为x°,
根据题意得180-x=6(90-x),
解得x=72.
答:这个角的度数是72°.
23.解析 因为点C,E分别是线段AD,BD的中点,
所以CD=AC=5,DE=BD=1.5,
所以CE=CD+DE=5+1.5=6.5.
24.解析 (1)北偏东70°.
(2)因为∠AOB=40°+15°=55°,∠AOC=∠AOB,
所以∠AOC=55°,所以∠BOC=110°.
因为射线OD是OB的反向延长线,
所以∠BOD=180°.
所以∠COD=180°-110°=70°.
因为OE平分∠COD,
所以∠COE=35°.
因为∠AOC=55°,
所以∠AOE=35°+55°=90°.
25.解析 (1)6;6.
(2)MN的长不会发生改变.
设点P表示的有理数是a(a>-6且a≠3).
当-6易知AP=a+6,BP=3-a,
因为M是线段AP上靠近点A的三等分点,N是线段BP上靠近点B的三等分点,
所以MP=AP=(a+6),NP=BP=(3-a),
所以MN=MP+NP=6;
当a>3时,如图,
易知AP=a+6,BP=a-3,
因为M是线段AP上靠近点A的三等分点,N是线段BP上靠近点B的三等分点,
所以MP=AP=(a+6),NP=BP=(a-3),
所以MN=MP-NP=6.
综上所述,点P在射线AB上运动(不与点A,B重合)的过程中,MN的长为定值6.
26.解析 (1)由已知得∠BOM=180°-∠AOM=150°,
因为∠MON是直角,OC平分∠BOM,所以∠CON=∠MON-∠BOM=90°-×150°=15°.
(2)∠CON=α.
详解:由已知得∠BOM=180°-∠AOM=180°-α,
因为∠MON是直角,OC平分∠BOM,
所以∠CON=∠MON-∠BOM=90°-×(180°-α)=α.
(3)设∠AOM=β,则∠BOM=180°-β.
①结论:∠AOM=2∠CON.
理由如下:
因为OC平分∠BOM,
所以∠MOC=∠BOM=(180°-β)=90°-β,
因为∠MON=90°,
所以∠CON=∠MON-∠MOC=90°-=β,
所以∠AOM=2∠CON.
②∠BON=∠MON-∠BOM=90°-(180°-β)=β-90°,由①可知∠AOC=∠AOM+∠MOC=β+90°-β=90°+β,
因为∠AOC=3∠BON,所以90°+β=3(β-90°),
解得β=144°,
所以∠AOM=144°.
21世纪教育网(www.21cnjy.com)
2024人教版数学七年级上学期同步练习
第四章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共30分)
1.【新独家原创】同学们用过下图这种折扇吧 因为它折起来便于携带,所以受到人们的喜爱.折扇展开的过程运用了数学上的 原理. ( )
A.点动成线
B.线动成面
C.面动成体
D.面与面相交的地方是线
2.(2022湖北随州中考)如图所示的是一个放在水平桌面上的半球体,该几何体从不同的方向看到的图形完全相同的是 ( )
A.从正面看和从左面看
B.从正面看和从上面看
C.从左面看和从上面看
D.从各个方向看
3.(2022四川自贡中考)如图,将长方形纸片ABCD绕边CD所在直线旋转一周,得到的立体图形是 ( )
A B
C D
4.如图所示,小于平角的角有 ( )
A.9个 B.8个
C.7个 D.6个
5.(2022山东临沂沂水期末)如图,OA表示北偏东25°方向,OB表示南偏西50°方向,则∠AOB的度数是 ( )
A.165° B.155°
C.135° D.115°
6.(2023四川达州达川期末)宣传委员制作黑板报时想要在黑板上画出一条笔直的参照线,由于尺子不够长,她想出了一个办法:在一根长度合适的毛线上涂满粉笔灰,两个同学分别抓住毛线两端,绷紧,靠近黑板要画线的位置,在中间将线一拉再松开,毛线弹回到黑板上,这样黑板上就出现了一条笔直的“粉笔灰线”,这种画法的数学依据是 ( )
A.两点之间,线段最短
B.两点确定一条直线
C.线段的中点的定义
D.两点间的距离的定义
7.(2023湖南郴州汝城校级期末)如图,若∠AOB>∠COD,则∠AOD与∠BOC的大小关系是 ( )
A.∠AOD=∠BOC
B.∠AOD<∠BOC
C.∠AOD>∠BOC
D.不能确定
8.(2022江苏泰州中考)如图所示的是一个几何体的展开图,则该几何体是 ( )
A.三棱锥 B.四棱锥
C.四棱柱 D.圆锥
9.射线OA上有B、C两点,若OB=8,BC=2,线段OB、BC的中点分别为D、E,则线段DE的长为 ( )
A.5 B.1或3
C.1 D.5或3
10.(2023辽宁沈阳铁西期末)每天中午11点30分“校园之声”节目都会如约而至,11点30分时时针与分针所夹的角为 ( )
A.170° B.175° C.165° D.160°
二、填空题(每小题3分,共30分)
11.(2022浙江杭州模拟)子弹从枪膛中射出去的轨迹可看成一条线,这说明 的数学道理.
12.已知线段AB=6 cm,延长线段AB到C,使BC=AB,反向延长线段AB到D,使AD=AC,则线段CD的长为 .
13.(2022山东济南历下期末)计算:30°12'= °.
14.【新情境·全向十字路口】(2023北京石景山期末)北京首个全向十字路口设于石景山区,为行人带来了很多便利.从上面看得到的平面图形如图所示.若想走近路,从位置A到位置C的两条路径“A→C”和“A→B→C”中选,你会选择路径 ,选择的依据是 .
15.(2022北京通州期末)如图,棋盘上有黑、白两色棋子若干,若直线l经过3枚颜色相同的棋子,则这样的直线共有 条.
16.【跨学科·生物】(2023吉林长春双阳期末)大自然中存在着许多奇妙的现象,科学家通过观察惊奇地发现,植物的茎叶和果实几乎都是按照137°30'的模式排列的.这样,植物的茎叶和果实就可以占有最大的空间,以获取最多的阳光,承接最多的雨水.以上描述中的137°30'的补角是 °.
17.(2022天津北辰期末)如图,辰辰同学根据这个图形写出了四个结论:①图中有两条直线;②图中有5条线段;③射线AC和射线AD是同一条射线;④直线BD经过点C.其中正确的结论是 .(填序号)
18.(2021湖北黄冈期末)如图,将一副直角三角板叠放在一起,使直角顶点重合于点O,则∠AOB+∠DOC= 度.
19.(2023山东菏泽曹县期末)如图,点C,D在线段AB上,且AC=CD=DB,点E是线段DB的中点,若CE=12 cm,则AB的长为 .
20.(2022安徽合肥蜀山期末)在同一平面内,∠AOC=∠BOD=50°,射线OB在∠AOC的内部,且∠AOB=20°,OE平分∠AOD,则∠COE的度数是 .
三、解答题(共40分)
21.(5分)如图,已知不在同一直线上的四个点A、B、C、D.
(1)画直线AD;
(2)连接AB;
(3)画射线CD;
(4)延长线段BA至点E,使BE=2BA;
(5)反向延长射线CD至点F,使DC=2CF.
22.(2022北京东城期末)(5分)若一个角的补角是它的余角的6倍,求这个角的度数.
23.(2023北京昌平期末)(6分)如图,C,D,E是线段AB上的点,AC=5,BD=3,点C,E分别是线段AD,BD的中点,求CE的长.
24.(2022广西玉林博白期末)(8分)如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.
(1)射线OC的方向是 ;
(2)若射线OE平分∠COD,求∠AOE的度数.
25.(8分)如图,数轴上点A,B表示的有理数分别为-6,3,若点P是射线AB上一个动点(不与点A,B重合),M是线段AP上靠近点A的三等分点,N是线段BP上靠近点B的三等分点.
(1)当点P表示的有理数是0时,MN的长为 ,当点P表示的有理数是6时,MN的长为 ;
(2)点P在射线AB上运动(不与点A,B重合)的过程中,MN的长是否发生改变 若不改变,请写出求MN的长的过程;若改变,请说明理由.
26.(8分)点O为直线AB上一点,将一直角三角板OMN的直角顶点放在点O处,射线OC平分∠BOM.
(1)如图1,若∠AOM=30°,求∠CON的度数;
(2)在图1中,若∠AOM=α,直接写出∠CON的度数(用含α的式子表示);
(3)将图1中的直角三角板OMN绕点O顺时针旋转至图2的位置,一边OM在直线AB上方,另一边ON在直线AB下方.
①探究∠AOM和∠CON的度数之间的关系,写出你的结论,并说明理由;
②当∠AOC=3∠BON时,求∠AOM的度数.
图1 图2
答案全解全析
一、选择题
1.B 开始的状态可以看成线,结束的状态可以看成面,所以运用了线动成面的原理.
2.A 该几何体从正面看和从左面看均为半圆,故选A.
3.A 将长方形纸片ABCD绕边CD所在直线旋转一周,可知旋转后有两个平的面,所以得到的立体图形是圆柱体.
4.C 符合条件的角中,以A为顶点的角有1个,以B为顶点的角有2个,以C为顶点的角有1个,以D为顶点的角有1个,以E为顶点的角有2个,共有1+2+1+1+2=7个,故选C.
5.B 由题意得∠AOB=25°+90°+(90°-50°)=155°.
6.B 这种画法的数学依据是两点确定一条直线.故选B.
7.C 因为∠AOB>∠COD,∠AOD=∠AOB+∠BOD,∠BOC=∠COD+∠BOD,
所以∠AOD>∠BOC.
8.B 根据展开图可以得出该几何体是四棱锥,故选B.
9.D 因为OB=8,D是OB的中点,
所以DB=4,
因为BC=2,E是BC的中点,
所以BE=1.
如图1,DE=BD-BE=3;
如图2,DE=BD+BE=5.故选D.
图1
图2
10.C 6×30°-×30°=180°-15°=165°,
所以时针与分针所夹的角为165°.故选C.
二、填空题
11.点动成线
12.18 cm
解析 AC=AB+BC=6+×6=9(cm),则CD=AD+AC=2AC=2×9=18(cm).
13.30.2
解析 因为1°=60',所以12'=0.2°,所以30°12'=30.2°.
14.A→C;两点之间,线段最短
15.3
解析 如图所示:
所以满足条件的直线共有3条.
16.42.5
解析 180°-137°30'=42°30'=42.5°.
17.①③
解析 题图中有两条直线:直线BD,直线BC;
题图中有6条线段:线段AB,线段BC,线段BD,线段AC,线段CD,线段AD;射线AC和射线AD的端点和方向都相同,是同一条射线;直线BD不经过点C.
故正确的结论是①③.
18.180
解析 ∠AOB+∠DOC=∠AOD+∠DOC+∠BOC+∠DOC=∠AOC+∠DOB=90°+90°=180°.
19.24 cm
解析 因为AC=CD=DB,点E是线段DB的中点,
所以AB=AD+DB=(AC+CD)+(DE+BE)=2(CD+DE)=2CE=24 cm.
20.15°或65°
解析 ①当OD与OC在OA的同侧时,
如图,
因为∠AOC=∠BOD=50°,∠AOB=20°,
所以∠AOD=∠BOD+∠AOB=70°,
因为OE平分∠AOD,
所以∠AOE=∠AOD=35°,
所以∠COE=∠AOC-∠AOE=15°;
②当OD与OC在OA的异侧时,
如图,
因为∠AOC=∠BOD=50°,∠AOB=20°,
所以∠AOD=∠BOD-∠AOB=30°,
因为OE平分∠AOD,
所以∠AOE=∠AOD=15°,
所以∠COE=∠AOC+∠AOE=65°.
综上所述,∠COE的度数为15°或65°.
三、解答题
21.解析 (1)(2)(3)(4)(5)如图所示.
22.解析 设这个角的度数为x°,
根据题意得180-x=6(90-x),
解得x=72.
答:这个角的度数是72°.
23.解析 因为点C,E分别是线段AD,BD的中点,
所以CD=AC=5,DE=BD=1.5,
所以CE=CD+DE=5+1.5=6.5.
24.解析 (1)北偏东70°.
(2)因为∠AOB=40°+15°=55°,∠AOC=∠AOB,
所以∠AOC=55°,所以∠BOC=110°.
因为射线OD是OB的反向延长线,
所以∠BOD=180°.
所以∠COD=180°-110°=70°.
因为OE平分∠COD,
所以∠COE=35°.
因为∠AOC=55°,
所以∠AOE=35°+55°=90°.
25.解析 (1)6;6.
(2)MN的长不会发生改变.
设点P表示的有理数是a(a>-6且a≠3).
当-6
因为M是线段AP上靠近点A的三等分点,N是线段BP上靠近点B的三等分点,
所以MP=AP=(a+6),NP=BP=(3-a),
所以MN=MP+NP=6;
当a>3时,如图,
易知AP=a+6,BP=a-3,
因为M是线段AP上靠近点A的三等分点,N是线段BP上靠近点B的三等分点,
所以MP=AP=(a+6),NP=BP=(a-3),
所以MN=MP-NP=6.
综上所述,点P在射线AB上运动(不与点A,B重合)的过程中,MN的长为定值6.
26.解析 (1)由已知得∠BOM=180°-∠AOM=150°,
因为∠MON是直角,OC平分∠BOM,所以∠CON=∠MON-∠BOM=90°-×150°=15°.
(2)∠CON=α.
详解:由已知得∠BOM=180°-∠AOM=180°-α,
因为∠MON是直角,OC平分∠BOM,
所以∠CON=∠MON-∠BOM=90°-×(180°-α)=α.
(3)设∠AOM=β,则∠BOM=180°-β.
①结论:∠AOM=2∠CON.
理由如下:
因为OC平分∠BOM,
所以∠MOC=∠BOM=(180°-β)=90°-β,
因为∠MON=90°,
所以∠CON=∠MON-∠MOC=90°-=β,
所以∠AOM=2∠CON.
②∠BON=∠MON-∠BOM=90°-(180°-β)=β-90°,由①可知∠AOC=∠AOM+∠MOC=β+90°-β=90°+β,
因为∠AOC=3∠BON,所以90°+β=3(β-90°),
解得β=144°,
所以∠AOM=144°.
21世纪教育网(www.21cnjy.com)
