沪教版六年级下第五章 有理数5.7有理数的除法4课件
文档属性
| 名称 | 沪教版六年级下第五章 有理数5.7有理数的除法4课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 895.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-09 00:00:00 | ||
图片预览











文档简介
课件33张PPT。有理数的除法1.7 6个同样大小的苹果平均分给3个小孩,每个小孩分到几个苹果?6÷3=2,每个小孩分到2个苹果因为2×3=6,所以6÷3=2. (-6) ÷3等于多少呢? 6 ÷(-3)等于多少呢?
(-6)÷(-3)等于多少呢? 从上面分苹果的例子受到启发,由于(-2)×3=-6,因此很自然地规定(-6)÷3=-2
类似地,由于(-2)×(-3)=6, 2×(-3)=-6,
因此很自然地规定: 6÷(-3)=-2, (-6)÷ (-3)=2. 从这些例子受到启发,抽象出有理数的除法运算;
对于两个有理数a,b,其中b≠0,如果有一个有理数c,使得cb = a,那么规定a÷b=c,把c叫作a除以b的商.同号两数相除得正数,异号两数相除
得负数,并且把它们的绝对值相除.0除以任何一个不等于0的数都得0. 例1 计算:
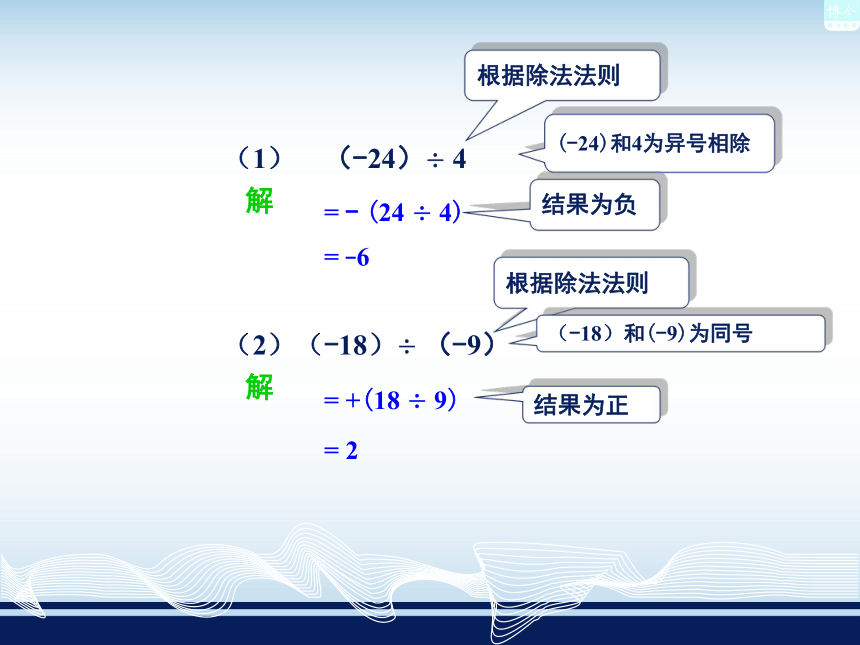
(1)(-24)÷4 ;
(2)(-18)÷(-9);
(3) 50 ÷(-5);
(4) 0÷(-8.8).举
例解(1) (-24)÷ 4= - (24 ÷ 4)根据除法法则(-24)和4为异号相除结果为负解(2)(-18)÷ (-9)= +(18 ÷ 9)根据除法法则(-18)和(-9)为同号结果为正= -6= 2解(3) 50÷(-5)= -(50 ÷ 5)根据除法法则50和(-5)为异号相除结果为负解(4) 0 ÷(-8.8)= 0根据除法法则0除以任何不等于0的数都得0= -10 一般地,如果两个数的乘积等于1,那么把其中一个数叫作另一个数的倒数,也称它们互为倒数. 试问:10÷ 可以怎样计算 ? 由于 因此除以一个不等于0的数等于乘上这个数的倒数.这个法则也可以表示成: 例2 计算:
(1) ;
(2) ;
(3) .举
例解(1)= (-12)×3根据除法法则 的倒数是3异号相乘,结果为负解(2)=根据除法法则 的倒数是异号相乘,结果为负= -36= -35解(3)= 根据除法法则 的倒数是同号相乘,结果为正= 1.计算: (1)14÷(-7); (2)(-2)÷(-7);
(3)(-72)÷6; (4) 0÷ (-0.001).
1.解(1)14 ÷ (-7)= -2;(2)(-2)÷(-7)= ;(3)(-72)÷6 = -12;(4) 0 ÷ (-0.001) = 0. 2.填空: (1)因为 × = 1,所以 的倒数是 ;
(2)因为 × = 1,所以 的倒数是 .-6-6 3.计算: (1) ; (2) ;
(3) ; (4) .
3.解(1) ;(2) ;(3) ;(4) . 例3 计算:
(1)(-56)÷(-2) ÷(-8);
(2)(-3.2)÷ 0.8 ÷(-2).举
例解(1)(-56)÷(-2) ÷(-8)= 28 ÷(-8)可以依次计算先算前两位数异号相除,结果为负解(2)(-3.2)÷ 0.8 ÷(-2)=(-4)÷(-2)可以依次计算异号相除为负同号相除为正= 2= 例4 计算:
(1)(-10)÷(-5) ×(-2);
(2) .举
例解(1)(-10)÷(-5) ×(-2)= 2 ×(-2)再算乘法先算前两位数,同号相除为正异号相乘,结果为负解(2)=先算前两位,同号相乘为正再算除法异号相乘为负= -4= 1.计算: (1)24÷(-3)÷(-4) ; (2)(-6)÷(-2)÷3;
(3)2÷(-7)÷(-4); (4) 18÷6÷(-2).
1.解(1)24÷(-3)÷(-4)= -8 ÷(-4)= 2 ;(2)(-6)÷(-2)÷3 = 3÷3 = 1 ;(3)2÷(-7)÷(-4) = ÷(-4) = ;(4)18 ÷6 ÷(-2) = 3÷(-2)= . 2.计算: (1) ;
(2) .
2.解(2) .(1) ;例1 计算: .有理数的除法法则
两个有理数相除,同号得正,异号得负,并把绝对值相除.
0除以任何非0的数都得0.
除以一个数等于乘以这个数的倒数,即a÷b= a · (b≠0).分析 原式=-11×(-13)×(-13)
=-11×13×13
=-1859-1859解例2 已知|x|=4,|y|= ,且 xy < 0,则 的值等于 .-8例3 在等式3×□-2×□=15的两个方格内分别填入一个数,使这两个数是互为相反数且等式成立,则第一个方格内的数是 .设第一个方格的数为a,则第二个方格数为(-a),则有
3a-2×(-a)= 15
5a = 15
a = 3.
故,第一个方格内的数是33解结 束
(-6)÷(-3)等于多少呢? 从上面分苹果的例子受到启发,由于(-2)×3=-6,因此很自然地规定(-6)÷3=-2
类似地,由于(-2)×(-3)=6, 2×(-3)=-6,
因此很自然地规定: 6÷(-3)=-2, (-6)÷ (-3)=2. 从这些例子受到启发,抽象出有理数的除法运算;
对于两个有理数a,b,其中b≠0,如果有一个有理数c,使得cb = a,那么规定a÷b=c,把c叫作a除以b的商.同号两数相除得正数,异号两数相除
得负数,并且把它们的绝对值相除.0除以任何一个不等于0的数都得0. 例1 计算:
(1)(-24)÷4 ;
(2)(-18)÷(-9);
(3) 50 ÷(-5);
(4) 0÷(-8.8).举
例解(1) (-24)÷ 4= - (24 ÷ 4)根据除法法则(-24)和4为异号相除结果为负解(2)(-18)÷ (-9)= +(18 ÷ 9)根据除法法则(-18)和(-9)为同号结果为正= -6= 2解(3) 50÷(-5)= -(50 ÷ 5)根据除法法则50和(-5)为异号相除结果为负解(4) 0 ÷(-8.8)= 0根据除法法则0除以任何不等于0的数都得0= -10 一般地,如果两个数的乘积等于1,那么把其中一个数叫作另一个数的倒数,也称它们互为倒数. 试问:10÷ 可以怎样计算 ? 由于 因此除以一个不等于0的数等于乘上这个数的倒数.这个法则也可以表示成: 例2 计算:
(1) ;
(2) ;
(3) .举
例解(1)= (-12)×3根据除法法则 的倒数是3异号相乘,结果为负解(2)=根据除法法则 的倒数是异号相乘,结果为负= -36= -35解(3)= 根据除法法则 的倒数是同号相乘,结果为正= 1.计算: (1)14÷(-7); (2)(-2)÷(-7);
(3)(-72)÷6; (4) 0÷ (-0.001).
1.解(1)14 ÷ (-7)= -2;(2)(-2)÷(-7)= ;(3)(-72)÷6 = -12;(4) 0 ÷ (-0.001) = 0. 2.填空: (1)因为 × = 1,所以 的倒数是 ;
(2)因为 × = 1,所以 的倒数是 .-6-6 3.计算: (1) ; (2) ;
(3) ; (4) .
3.解(1) ;(2) ;(3) ;(4) . 例3 计算:
(1)(-56)÷(-2) ÷(-8);
(2)(-3.2)÷ 0.8 ÷(-2).举
例解(1)(-56)÷(-2) ÷(-8)= 28 ÷(-8)可以依次计算先算前两位数异号相除,结果为负解(2)(-3.2)÷ 0.8 ÷(-2)=(-4)÷(-2)可以依次计算异号相除为负同号相除为正= 2= 例4 计算:
(1)(-10)÷(-5) ×(-2);
(2) .举
例解(1)(-10)÷(-5) ×(-2)= 2 ×(-2)再算乘法先算前两位数,同号相除为正异号相乘,结果为负解(2)=先算前两位,同号相乘为正再算除法异号相乘为负= -4= 1.计算: (1)24÷(-3)÷(-4) ; (2)(-6)÷(-2)÷3;
(3)2÷(-7)÷(-4); (4) 18÷6÷(-2).
1.解(1)24÷(-3)÷(-4)= -8 ÷(-4)= 2 ;(2)(-6)÷(-2)÷3 = 3÷3 = 1 ;(3)2÷(-7)÷(-4) = ÷(-4) = ;(4)18 ÷6 ÷(-2) = 3÷(-2)= . 2.计算: (1) ;
(2) .
2.解(2) .(1) ;例1 计算: .有理数的除法法则
两个有理数相除,同号得正,异号得负,并把绝对值相除.
0除以任何非0的数都得0.
除以一个数等于乘以这个数的倒数,即a÷b= a · (b≠0).分析 原式=-11×(-13)×(-13)
=-11×13×13
=-1859-1859解例2 已知|x|=4,|y|= ,且 xy < 0,则 的值等于 .-8例3 在等式3×□-2×□=15的两个方格内分别填入一个数,使这两个数是互为相反数且等式成立,则第一个方格内的数是 .设第一个方格的数为a,则第二个方格数为(-a),则有
3a-2×(-a)= 15
5a = 15
a = 3.
故,第一个方格内的数是33解结 束
