沪教版六年级下第五章 有理数5.3绝对值课件
文档属性
| 名称 | 沪教版六年级下第五章 有理数5.3绝对值课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 383.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-10 00:00:00 | ||
图片预览




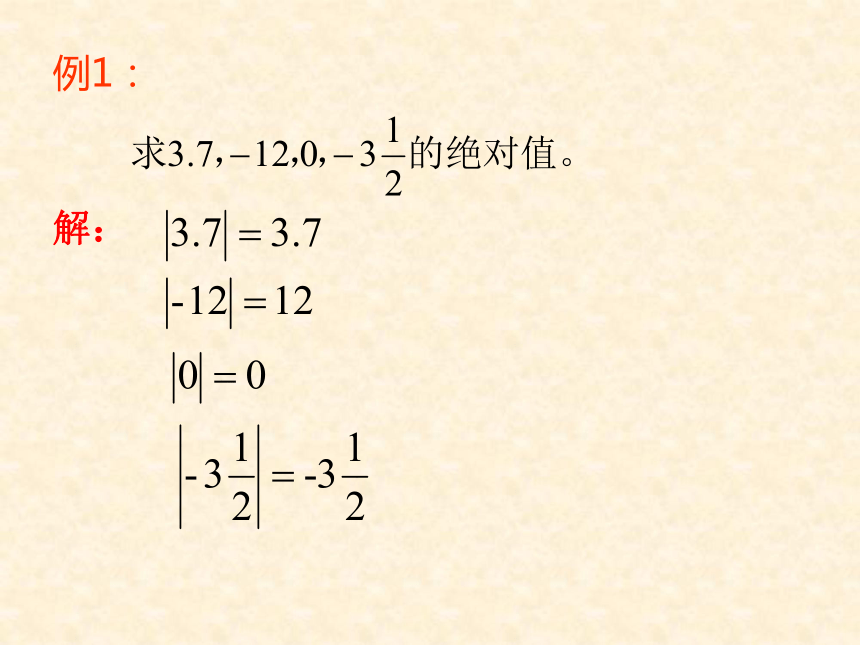


文档简介
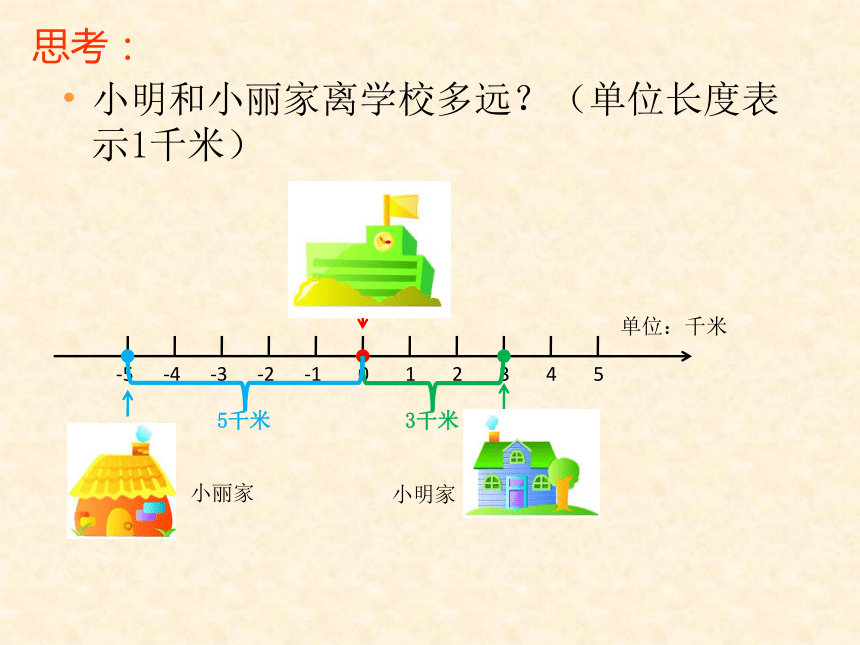
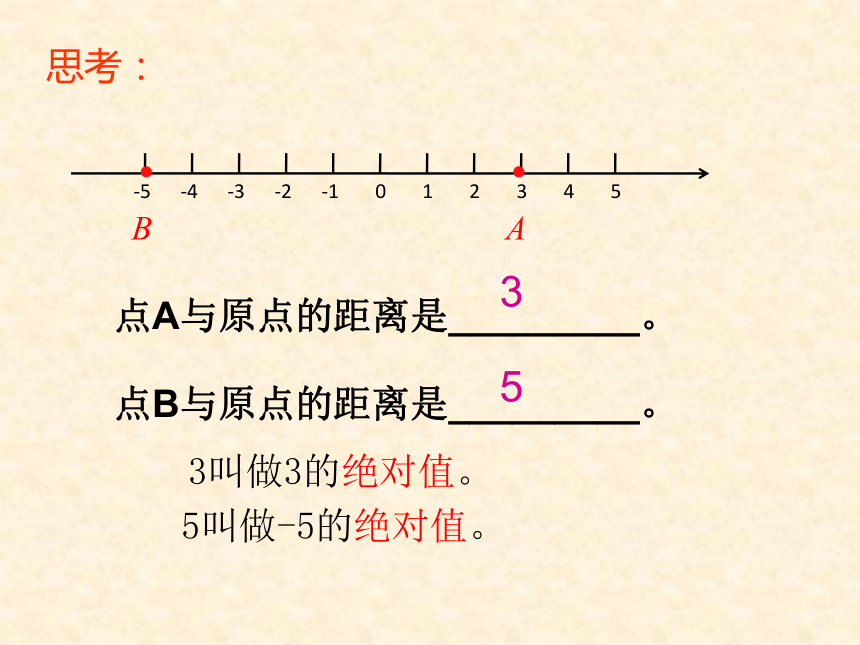
课件29张PPT。5.3 绝对值蓝天民办小学 夏丽平 伍贤军思考:小明和小丽家离学校多远?(单位长度表示1千米)小明家小丽家单位:千米3千米5千米点A与原点的距离是_________。 点B与原点的距离是_________。 思考:353叫做3的绝对值。5叫做-5的绝对值。定义: 一个数在数轴上所对应的点与原点的距离,叫做这个数的绝对值。绝对值一般用符号“| |”表示。如:|a|表示数a的绝对值。
填空:|4|=44的绝对值是____,记作__________。 4-3的绝对值是____,记作__________。 0的绝对值是____,记作__________。 30|-3|=3|0|=0观察思考:正数、负数、0的绝对值分别是什么?概括:一个正数的绝对值是它本身;
一个负数的绝对值是它的相反数;
零的绝对值是零。例1:解:(2)当a是负数时,|a|= (1)当a是正数时,|a|=(3)当a=0时,|a|=a-a0总结:(3)任何一个有理数都有绝对值吗?一个数的绝对值有几个?
(4)绝对值等于2的数有几个?它们是什么?
任何一个有理数都有绝对值。一个数的绝对值只有1个。绝对值等于2的数有两个。它们是2和-2。思考:(5)有没有一个数的绝对值等于-2?没有一个数的绝对值等于-2。任何一个数的绝对值一定是非负数。|a|≥0思考:(6)任何一个数它的绝对值一定是怎样的数?1.若|a|= 3 ,那么a =
2.若|-b|=7,那么b=
±3±7练习:4.在数轴上,到原点的距离等于3.5个单位长度的点所表示的有理数是____________。5.__________的绝对值是它本身,________的绝对值是它的相反数。+3.5, -3.5正数和0负数和0(1)绝对值是6的数有___个,是_________;
(2)如果|x|=5,则x=________;
(3)绝对值最小的整数是______;
(4)写出绝对值小于3的整数_________;
(5) |-22.8|=_____,-|-7.5|=______6和-65或-50-2,-1,0,1,222.8-7.5练习:(1)数a的绝对值在数轴上表示什么意义?
(2)互为相反数的两个数的绝对值有什么关系? 表示数a在数轴上所对应的点与原点的距离。互为相反数的两个数的绝对值相等。思考:观察:观察数轴上的数字,发现数的大小跟它们在数轴上的位置有什么关系?越 来 越 大数轴上右边的点表示的数总比左边的点表示的数大正数大于零零大于负数正数大于负数例2:用数轴上的点表示下列各数,并将它们从小到大排列起来:
解:例3:解:观察: 观察数轴上的数字,发现它们绝对值的大小跟它们在数轴上的点与原点的距离有什么关系? 一个数所表示的点离开原点距离越远,其绝对值越大,离开原点越近,其绝
对值越小。思考:解:观察思考: 两个正数的绝对值跟正数本身的大小有什么关系?两个正数,绝对值大的那个数就大。结论:越 来 越 大思考:解:观察思考: 两个负数的绝对值跟负数本身的大小有什么关系?两个负数,绝对值大的那个数反而小。结论:越 来 越 大课堂小结 一个数在数轴上所对应的点与原点的距离,叫做这个数的绝对值。
比较两个数的大小:1.两个正数比较大小,绝对值大的数就大。2.两个负数比较大小,绝对值大的数反而小。3.正数和负数比较大小,正数大于负数。4.正数和0比较大小,正数大于0。5.负数和0比较大小,0大于负数。 写出绝对值小于5的整数,并把它们表示在数轴上。练习:解: 绝对值小于5的整数有
-4,-3,-2,-1,0,1,2,3,44210-1-2-3-43当a为有理数时,- a一定表示负数吗?思考:<<>练习:比较大小练习:作业:
填空:|4|=44的绝对值是____,记作__________。 4-3的绝对值是____,记作__________。 0的绝对值是____,记作__________。 30|-3|=3|0|=0观察思考:正数、负数、0的绝对值分别是什么?概括:一个正数的绝对值是它本身;
一个负数的绝对值是它的相反数;
零的绝对值是零。例1:解:(2)当a是负数时,|a|= (1)当a是正数时,|a|=(3)当a=0时,|a|=a-a0总结:(3)任何一个有理数都有绝对值吗?一个数的绝对值有几个?
(4)绝对值等于2的数有几个?它们是什么?
任何一个有理数都有绝对值。一个数的绝对值只有1个。绝对值等于2的数有两个。它们是2和-2。思考:(5)有没有一个数的绝对值等于-2?没有一个数的绝对值等于-2。任何一个数的绝对值一定是非负数。|a|≥0思考:(6)任何一个数它的绝对值一定是怎样的数?1.若|a|= 3 ,那么a =
2.若|-b|=7,那么b=
±3±7练习:4.在数轴上,到原点的距离等于3.5个单位长度的点所表示的有理数是____________。5.__________的绝对值是它本身,________的绝对值是它的相反数。+3.5, -3.5正数和0负数和0(1)绝对值是6的数有___个,是_________;
(2)如果|x|=5,则x=________;
(3)绝对值最小的整数是______;
(4)写出绝对值小于3的整数_________;
(5) |-22.8|=_____,-|-7.5|=______6和-65或-50-2,-1,0,1,222.8-7.5练习:(1)数a的绝对值在数轴上表示什么意义?
(2)互为相反数的两个数的绝对值有什么关系? 表示数a在数轴上所对应的点与原点的距离。互为相反数的两个数的绝对值相等。思考:观察:观察数轴上的数字,发现数的大小跟它们在数轴上的位置有什么关系?越 来 越 大数轴上右边的点表示的数总比左边的点表示的数大正数大于零零大于负数正数大于负数例2:用数轴上的点表示下列各数,并将它们从小到大排列起来:
解:例3:解:观察: 观察数轴上的数字,发现它们绝对值的大小跟它们在数轴上的点与原点的距离有什么关系? 一个数所表示的点离开原点距离越远,其绝对值越大,离开原点越近,其绝
对值越小。思考:解:观察思考: 两个正数的绝对值跟正数本身的大小有什么关系?两个正数,绝对值大的那个数就大。结论:越 来 越 大思考:解:观察思考: 两个负数的绝对值跟负数本身的大小有什么关系?两个负数,绝对值大的那个数反而小。结论:越 来 越 大课堂小结 一个数在数轴上所对应的点与原点的距离,叫做这个数的绝对值。
比较两个数的大小:1.两个正数比较大小,绝对值大的数就大。2.两个负数比较大小,绝对值大的数反而小。3.正数和负数比较大小,正数大于负数。4.正数和0比较大小,正数大于0。5.负数和0比较大小,0大于负数。 写出绝对值小于5的整数,并把它们表示在数轴上。练习:解: 绝对值小于5的整数有
-4,-3,-2,-1,0,1,2,3,44210-1-2-3-43当a为有理数时,- a一定表示负数吗?思考:<<>练习:比较大小练习:作业:
