中位线(山西省临汾地区浮山县)
图片预览

文档简介
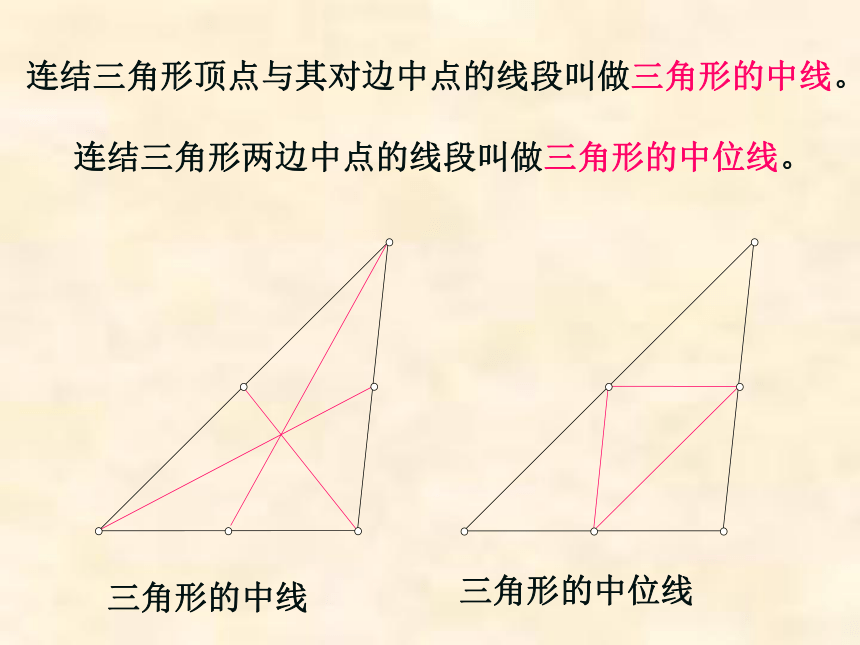
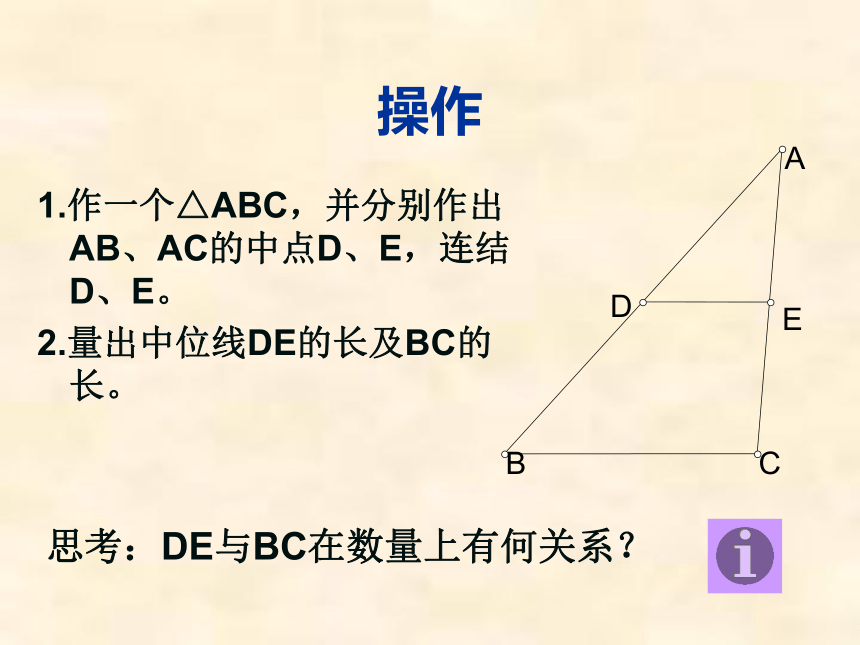
课件19张PPT。三角形的中位线三角形的中线三角形的中位线连结三角形两边中点的线段叫做三角形的中位线。连结三角形顶点与其对边中点的线段叫做三角形的中线。操作1.作一个△ABC,并分别作出AB、AC的中点D、E,连结D、E。
2.量出中位线DE的长及BC的长。
思考:DE与BC在数量上有何关系?
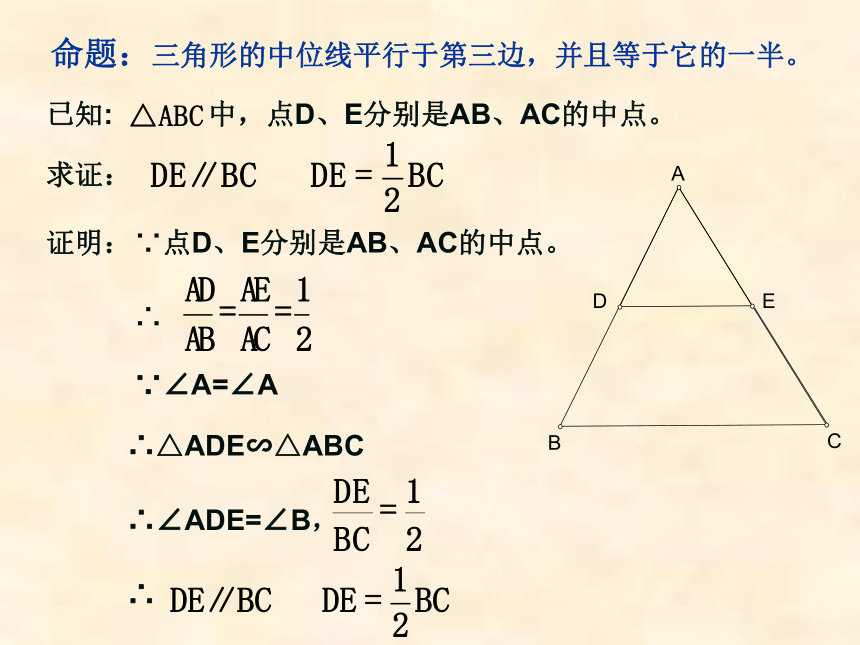
命题:三角形的中位线平行于第三边,并且等于它的一半。证明:∵点D、E分别是AB、AC的中点。∵∠A=∠A∴△ADE∽△ABC三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半。三角形中位线定理的数学语言表示为:
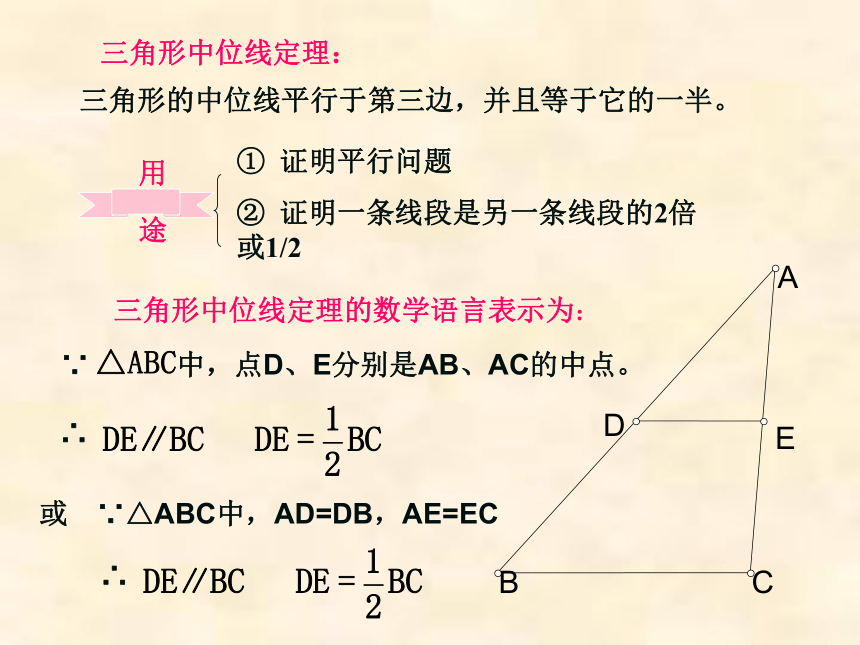
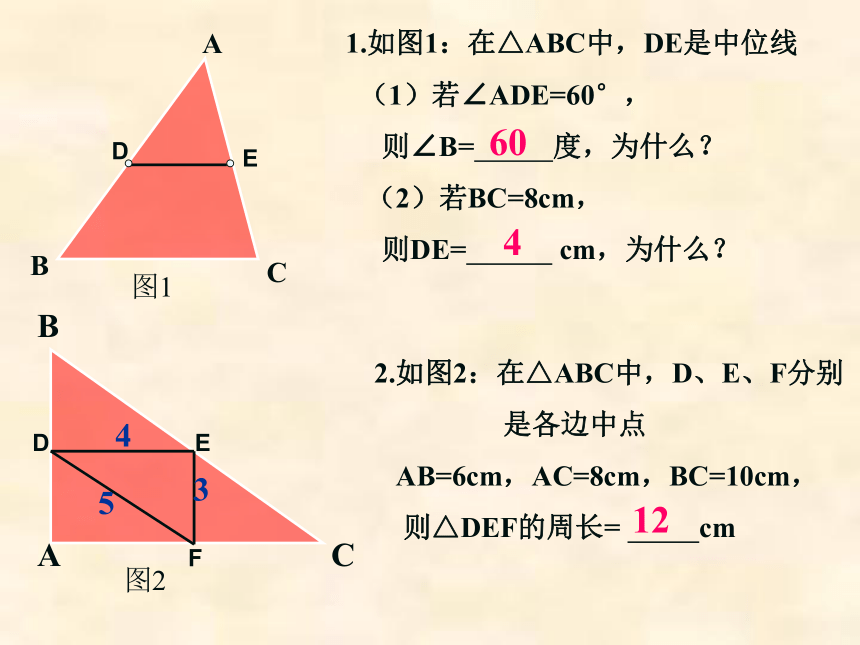
或 ∵△ABC中,AD=DB,AE=EC1.如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B= 度,为什么?
(2)若BC=8cm,
则DE= cm,为什么? 2.如图2:在△ABC中,D、E、F分别
是各边中点
AB=6cm,AC=8cm,BC=10cm,
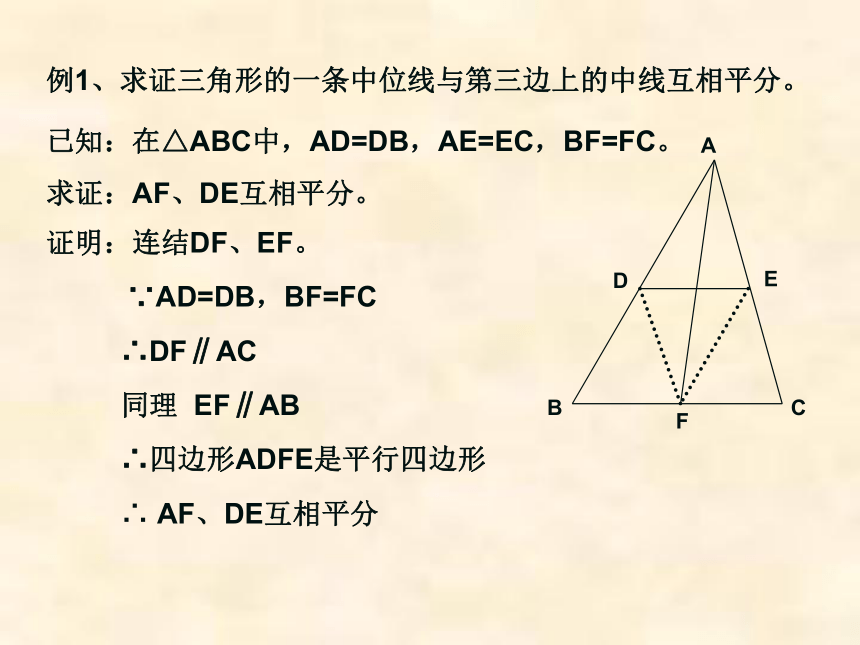
则△DEF的周长= cm图1图260412BAC543例1、求证三角形的一条中位线与第三边上的中线互相平分。已知:在△ABC中,AD=DB,AE=EC,BF=FC。求证:AF、DE互相平分。证明:连结DF、EF。∵AD=DB,BF=FC∴DF∥AC同理 EF∥AB∴四边形ADFE是平行四边形∴ AF、DE互相平分已知:在四边形ABCD中,E、F、G、H分别是AB、BC 、
CD、DA的中点例2.求证:顺次连结四边形各边中点所得的四边形是平行
四边形。 求证:四边形EFGH是平行四边形证明: 连结AC、BD∵AH=HD,CG=GD∴HG∥EF且 HG=EF∴四边形EFGH是平行四边形求证:顺次连结对角线互相垂直的四边形各边中点所得的
四边形是矩形。已知:四边形ABCD中,AC⊥BD,点
E、F、G、H分别为AB、BC、CD、
DA边上的中点求证:四边形EFGH是矩形。证明:∵AE=BE,AH=DH∴EH∥BD同理 FG∥BD,HG∥AC,EF∥AC∵AC⊥BD∴EH⊥HG,HG⊥FG,EF⊥FG∴∠EHG=∠HGF=∠EFG=90°∴四边形EFGH
是矩形练习一求证:顺次连结对角线相等的四边形各边中点所得的
四边形是菱形。已知:四边形ABCD中,AC=BD,点
E、F、G、H分别为AB、BC、CD、
DA边上的中点求证:四边形EFGH是菱形。证明:∵AE=BE,AH=DH∵AC=BD∴EH=EF=FG=GH∴四边形EFGH
是菱形练习二顺次连结四边形各边中点所得的四边形叫做中点四边形。归纳原四边形对角线互相垂直时,中点四边形是矩形。原四边形对角线相等时,中点四边形是菱形。中点四边形是平行四边形。①顺次连结平行四边形四边中点所得的四边形是————————②顺次连结等腰梯形四边中点所得的四边形是——————③顺次连结矩形四边中点所得的四边形是——————④顺次连结菱形四边中点所得的四边形是——————⑤顺次连结正方形四边中点所得的四边形是—————平行四边形菱形菱形矩形正方形练 习三角形重心性质用数学语言表示为:
∵点O为三角形ABC的重心已知:△ABC中,点O为△ABC的重心。证明:连接EF∵点O为△ABC的重心∴AE=BE,AF=CF∴△OEF∽△OCB练 习 在△ABC中,∠BAC=90°,D、E、F分别为BC、AC、AB
的中点,AD、BE、CF相交与O点,AB=6,AC=8,试求线段
OA、OE、OF的长度。解:在Rt△ABC中,∵D为BC边上的中点在Rt△ABE中,在Rt△AFC中,梯形的中位线:连结梯形两腰中点的线段。性质:梯形的中位线平行于两底边,并且等于
两底和的一半。梯形中位线定理的数学语言表示为:
∵梯形ABCD中,AE=EB,DF=FC已知:如图,在梯形ABCD中,AD∥BC,AE=BE,DF=CF证明:连结AF并延长与BC的延长线
交于点G则AD∥CG∴∠D=∠DCG∵∠AFD=∠CFG,DF=CF∴△ADF≌△GCF∴AF=FG,AD=CG∵AE=BE∵BG=BC+CG思 考 梯形的面积公式为( ),可变为( ),
它的几何意义为( )。 梯形的面积等于梯形的中
位线与高的积,它与以梯形的
中位线为长,梯形的高为宽的
矩形的面积相等。
小 结三角形的中位线:连结三角形两边中点的线段。三角形的中位线平行于第三边,并且等于它的一半。
2.量出中位线DE的长及BC的长。
思考:DE与BC在数量上有何关系?
命题:三角形的中位线平行于第三边,并且等于它的一半。证明:∵点D、E分别是AB、AC的中点。∵∠A=∠A∴△ADE∽△ABC三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半。三角形中位线定理的数学语言表示为:
或 ∵△ABC中,AD=DB,AE=EC1.如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B= 度,为什么?
(2)若BC=8cm,
则DE= cm,为什么? 2.如图2:在△ABC中,D、E、F分别
是各边中点
AB=6cm,AC=8cm,BC=10cm,
则△DEF的周长= cm图1图260412BAC543例1、求证三角形的一条中位线与第三边上的中线互相平分。已知:在△ABC中,AD=DB,AE=EC,BF=FC。求证:AF、DE互相平分。证明:连结DF、EF。∵AD=DB,BF=FC∴DF∥AC同理 EF∥AB∴四边形ADFE是平行四边形∴ AF、DE互相平分已知:在四边形ABCD中,E、F、G、H分别是AB、BC 、
CD、DA的中点例2.求证:顺次连结四边形各边中点所得的四边形是平行
四边形。 求证:四边形EFGH是平行四边形证明: 连结AC、BD∵AH=HD,CG=GD∴HG∥EF且 HG=EF∴四边形EFGH是平行四边形求证:顺次连结对角线互相垂直的四边形各边中点所得的
四边形是矩形。已知:四边形ABCD中,AC⊥BD,点
E、F、G、H分别为AB、BC、CD、
DA边上的中点求证:四边形EFGH是矩形。证明:∵AE=BE,AH=DH∴EH∥BD同理 FG∥BD,HG∥AC,EF∥AC∵AC⊥BD∴EH⊥HG,HG⊥FG,EF⊥FG∴∠EHG=∠HGF=∠EFG=90°∴四边形EFGH
是矩形练习一求证:顺次连结对角线相等的四边形各边中点所得的
四边形是菱形。已知:四边形ABCD中,AC=BD,点
E、F、G、H分别为AB、BC、CD、
DA边上的中点求证:四边形EFGH是菱形。证明:∵AE=BE,AH=DH∵AC=BD∴EH=EF=FG=GH∴四边形EFGH
是菱形练习二顺次连结四边形各边中点所得的四边形叫做中点四边形。归纳原四边形对角线互相垂直时,中点四边形是矩形。原四边形对角线相等时,中点四边形是菱形。中点四边形是平行四边形。①顺次连结平行四边形四边中点所得的四边形是————————②顺次连结等腰梯形四边中点所得的四边形是——————③顺次连结矩形四边中点所得的四边形是——————④顺次连结菱形四边中点所得的四边形是——————⑤顺次连结正方形四边中点所得的四边形是—————平行四边形菱形菱形矩形正方形练 习三角形重心性质用数学语言表示为:
∵点O为三角形ABC的重心已知:△ABC中,点O为△ABC的重心。证明:连接EF∵点O为△ABC的重心∴AE=BE,AF=CF∴△OEF∽△OCB练 习 在△ABC中,∠BAC=90°,D、E、F分别为BC、AC、AB
的中点,AD、BE、CF相交与O点,AB=6,AC=8,试求线段
OA、OE、OF的长度。解:在Rt△ABC中,∵D为BC边上的中点在Rt△ABE中,在Rt△AFC中,梯形的中位线:连结梯形两腰中点的线段。性质:梯形的中位线平行于两底边,并且等于
两底和的一半。梯形中位线定理的数学语言表示为:
∵梯形ABCD中,AE=EB,DF=FC已知:如图,在梯形ABCD中,AD∥BC,AE=BE,DF=CF证明:连结AF并延长与BC的延长线
交于点G则AD∥CG∴∠D=∠DCG∵∠AFD=∠CFG,DF=CF∴△ADF≌△GCF∴AF=FG,AD=CG∵AE=BE∵BG=BC+CG思 考 梯形的面积公式为( ),可变为( ),
它的几何意义为( )。 梯形的面积等于梯形的中
位线与高的积,它与以梯形的
中位线为长,梯形的高为宽的
矩形的面积相等。
小 结三角形的中位线:连结三角形两边中点的线段。三角形的中位线平行于第三边,并且等于它的一半。
