2023-2024学年华东师大版七年级 数学上册3.1.1 用字母表示数 同步练习(含答案)
文档属性
| 名称 | 2023-2024学年华东师大版七年级 数学上册3.1.1 用字母表示数 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 448.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-25 13:42:13 | ||
图片预览

文档简介
3.1.1 用字母表示数
一、单选题(每小题3分,共30分)
1.若b是有理数,则( )
A.b一定是正数 B.b正数,负数,0均有可能
C.一定是负数 D.b一定是0
2.一辆汽车小时行驶了千米,若此汽车的速度为千米/时,则以下结论正确的是( )
A. B. C. D.
3.两个数的和是30,其中一个数用字母表示,那么另外一个数是( )
A. B. C. D.
4.教室内有排座位,每排有个座位,则这个教室共有座位( )
A.个 B.个 C.个 D.个
5.若三角形的一条边长为,这条边上的高为,则这个三角形的面积可以表示为( )
A. B. C. D.
6.甲袋有a千克大米,乙袋有b千克大米,如果从甲袋拿出9千克大米放入乙袋,那么甲、乙两袋质量相等.列成等式是( ).
A. B. C. D.
7.苹果原价是每千克a元,现在按八折出售,假如现在要买,那么需要付费( )
A.元 B.元 C.元 D.元
8.若,则的值可表示为 ( )
A. B. C. D.
9.(是有理数)表示的数是( )
A.正数 B.负数 C.正数或负数 D.任意有理数
10.4个杯子叠起来高,6个杯子叠起来高,n个杯子叠起来的高度可以表示为( ).
A. B. C. D.
二、填空题(每小题3分,共30分)
11.一个长为5cm的长方形的周长为2(5+b)cm,则字母b表示的是___________.
12.若,则___________(用含式子表示).
13.观察下列算式:
; ;
; ; ……
若字母n表示正整数,请把第n个等式用含n的式子表示出来:___________.
14.观察下列式子:
;;;;;…
依此规律,则第(为正整数)个等式是___________.
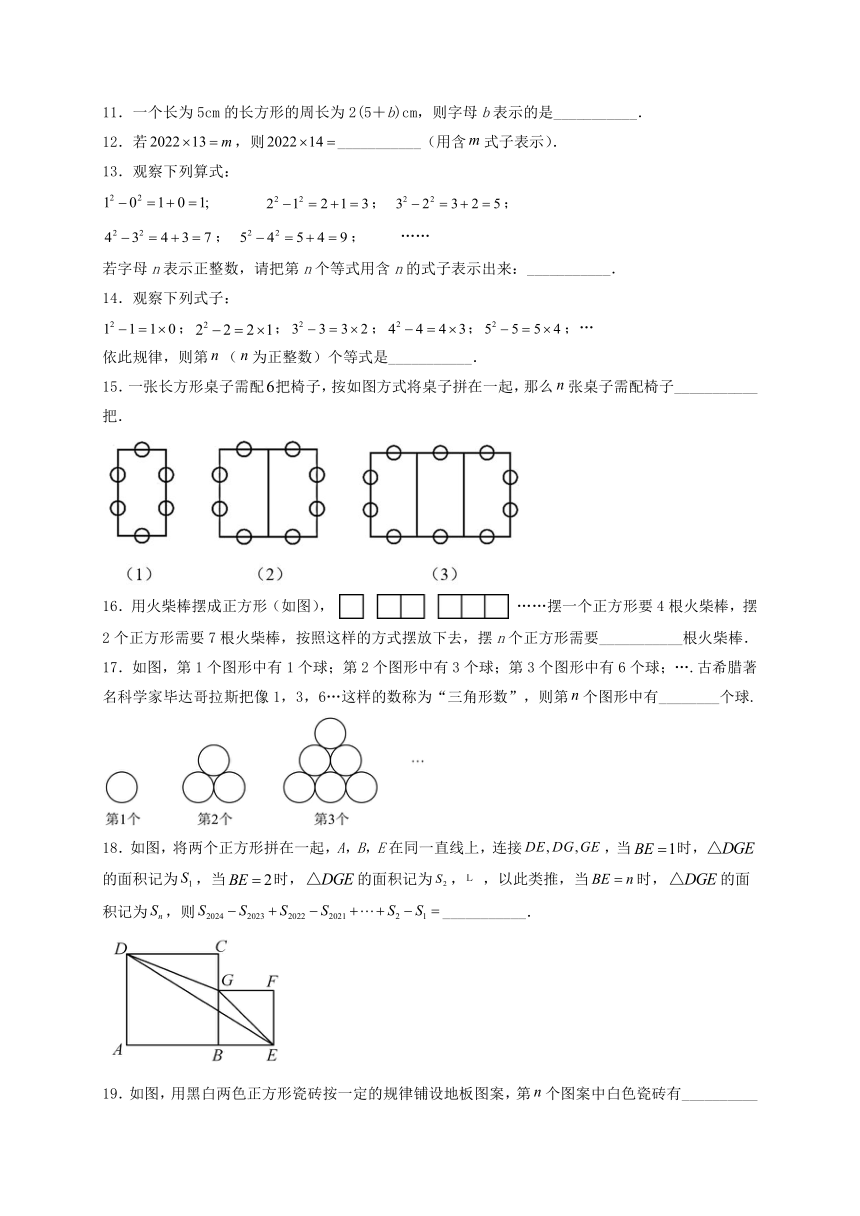
15.一张长方形桌子需配把椅子,按如图方式将桌子拼在一起,那么张桌子需配椅子___________把.
16.用火柴棒摆成正方形(如图), ……摆一个正方形要4根火柴棒,摆2个正方形需要7根火柴棒,按照这样的方式摆放下去,摆n个正方形需要___________根火柴棒.
17.如图,第1个图形中有1个球;第2个图形中有3个球;第3个图形中有6个球;….古希腊著名科学家毕达哥拉斯把像1,3,6…这样的数称为“三角形数”,则第个图形中有________个球.
18.如图,将两个正方形拼在一起,A,B,E在同一直线上,连接,当时,的面积记为,当时,的面积记为,,以此类推,当时,的面积记为,则___________.
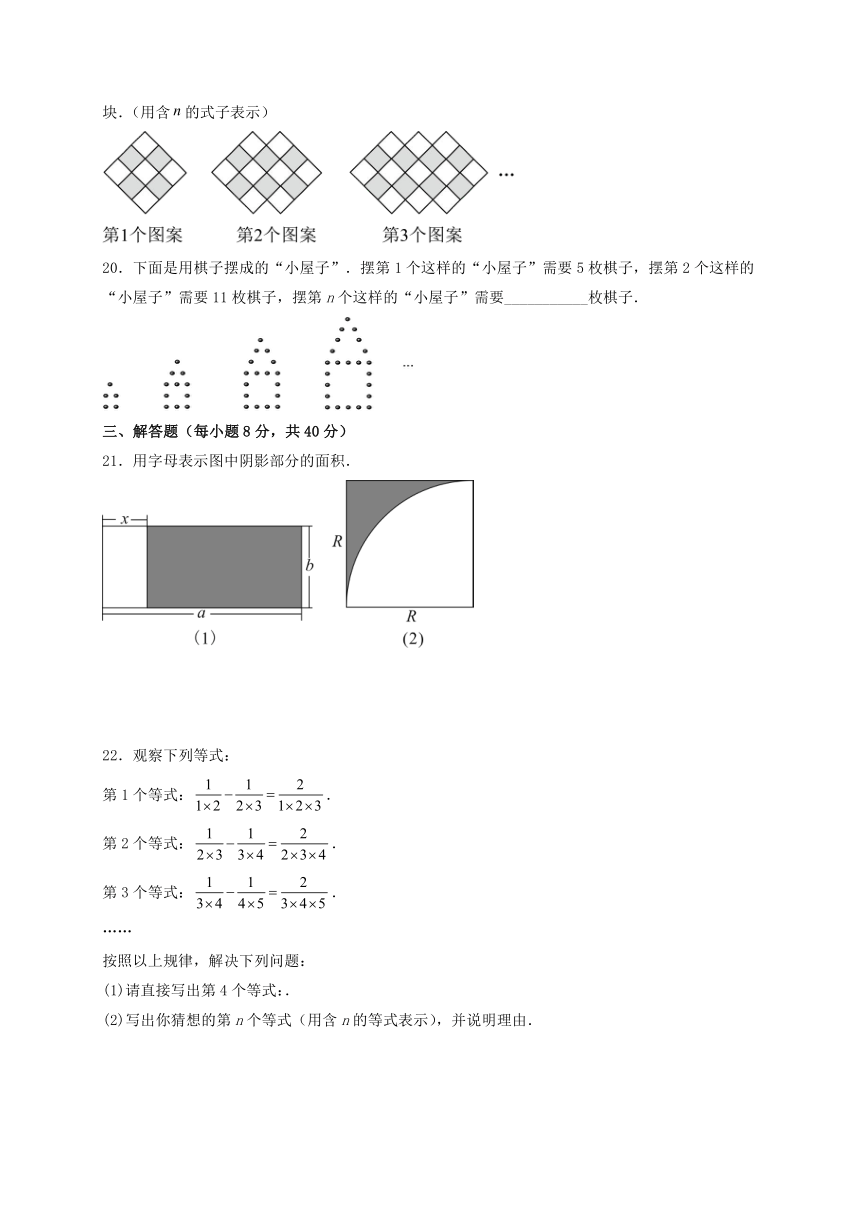
19.如图,用黑白两色正方形瓷砖按一定的规律铺设地板图案,第个图案中白色瓷砖有__________块.(用含的式子表示)
20.下面是用棋子摆成的“小屋子”.摆第1个这样的“小屋子”需要5枚棋子,摆第2个这样的“小屋子”需要11枚棋子,摆第n个这样的“小屋子”需要___________枚棋子.
三、解答题(每小题8分,共40分)
21.用字母表示图中阴影部分的面积.
22.观察下列等式:
第1个等式:.
第2个等式:.
第3个等式:.
……
按照以上规律,解决下列问题:
(1)请直接写出第4个等式:.
(2)写出你猜想的第n个等式(用含n的等式表示),并说明理由.
23.观察下列等式并回答问题:
;;;;……;
(1)可猜想第个的等式为______________________.
(2)若字母表示自然数,将第个的等式写出来,并验证其正确性.
24.用三角形和六边形按如图所示的规律拼图案.
(1)第5个图案中,三角形有________个,六边形有________个;
(2)第(为正整数)个图案中,三角形与六边形各有多少个?
(3)第2021个图案中,有多少个三角形?
(4)是否存在某个符合上述规律的图案,其中有100个三角形和40个六边形?如果存在,指出是第几个图案;如果不存在,请说明理由.
25.某种窗户由上下两部分组成,其上部是用木条围成的半圆形,且半圆形内部由三根等长的木条分隔,下部是用木条围成的边长相等的四个小正方形,木条的宽度和厚度不计.已知下部每个小正方形的边长为a米.
(1)用含a的代数式分别表示窗户的面积和所用木条的总长度;
(2)若米,窗户上安装的是玻璃,玻璃25元/平方米,木条20元/米,求制作这个窗户需要的总钱数(值取3,计算结果精确到个位).
参考答案
1.B 2.D 3.D 4.A 5.D 6.B 7.A 8.B 9.D 10.D
11.宽 12. 13. 14. 15.
16. 17. 18.1024650 19. 20.
21.【详解】解:(1)阴影部分的面积=ab﹣bx;
(2)阴影部分的面积=R2πR2.
22.【详解】(1)解:∵第1个等式为,
第2个等式为,
第3个等式为,
∴第4个等式为,
故答案为:;
(2)解:第n个等式为,
∵第1个等式为,
第2个等式为,
第3个等式为,
第4个等式为,
……,
∴第n个等式为.
23.【详解】(1)解:∵第个式子,第个式子,第个式子,第个式子,……,
∴第个式子为,
∴第个式子为,
故答案为;
(2)解:∵第个式子,第个式子,第个式子,第个式子,……,
∴第个式子为,理由如下:
∵,,
∴,
∴左边右边,
∴等式成立,
∴第个式子为.
24.【详解】(1)第1个图案中,三角形个,六边形有1个,
第2个图案中,三角形个,六边形有2个,
第3个图案中,三角形个,六边形有3个,
第4个图案中,三角形个,六边形有4个,
所以第5个图案中,三角形个,六边形有5个,
故答案为:12,5;
(2)由(1)可得,第n个图案中有三角形个,六边形有n个;
(3)第2021个图案中,
三角形有:(个);
(4)不存在,因为当时,而,
所以不存在某个符合上述规律的图案,其中有100个三形与40个六边形.
25.【详解】(1)S=2a×2aπa2=4a2πa2
即窗户的面积为(4a2πa2)米2.
15a+πa=(15+π)a(米)
即制作这种窗户所需材料的总长度(15+π)a(米).
(2)a=1时,25(4a2πa2)+20(15+π)a
≈25×(4×13×1)+20×(15+3)×1
=137.5+360
=497.5
≈498(元),即制作这扇窗户需要498元.
一、单选题(每小题3分,共30分)
1.若b是有理数,则( )
A.b一定是正数 B.b正数,负数,0均有可能
C.一定是负数 D.b一定是0
2.一辆汽车小时行驶了千米,若此汽车的速度为千米/时,则以下结论正确的是( )
A. B. C. D.
3.两个数的和是30,其中一个数用字母表示,那么另外一个数是( )
A. B. C. D.
4.教室内有排座位,每排有个座位,则这个教室共有座位( )
A.个 B.个 C.个 D.个
5.若三角形的一条边长为,这条边上的高为,则这个三角形的面积可以表示为( )
A. B. C. D.
6.甲袋有a千克大米,乙袋有b千克大米,如果从甲袋拿出9千克大米放入乙袋,那么甲、乙两袋质量相等.列成等式是( ).
A. B. C. D.
7.苹果原价是每千克a元,现在按八折出售,假如现在要买,那么需要付费( )
A.元 B.元 C.元 D.元
8.若,则的值可表示为 ( )
A. B. C. D.
9.(是有理数)表示的数是( )
A.正数 B.负数 C.正数或负数 D.任意有理数
10.4个杯子叠起来高,6个杯子叠起来高,n个杯子叠起来的高度可以表示为( ).
A. B. C. D.
二、填空题(每小题3分,共30分)
11.一个长为5cm的长方形的周长为2(5+b)cm,则字母b表示的是___________.
12.若,则___________(用含式子表示).
13.观察下列算式:
; ;
; ; ……
若字母n表示正整数,请把第n个等式用含n的式子表示出来:___________.
14.观察下列式子:
;;;;;…
依此规律,则第(为正整数)个等式是___________.
15.一张长方形桌子需配把椅子,按如图方式将桌子拼在一起,那么张桌子需配椅子___________把.
16.用火柴棒摆成正方形(如图), ……摆一个正方形要4根火柴棒,摆2个正方形需要7根火柴棒,按照这样的方式摆放下去,摆n个正方形需要___________根火柴棒.
17.如图,第1个图形中有1个球;第2个图形中有3个球;第3个图形中有6个球;….古希腊著名科学家毕达哥拉斯把像1,3,6…这样的数称为“三角形数”,则第个图形中有________个球.
18.如图,将两个正方形拼在一起,A,B,E在同一直线上,连接,当时,的面积记为,当时,的面积记为,,以此类推,当时,的面积记为,则___________.
19.如图,用黑白两色正方形瓷砖按一定的规律铺设地板图案,第个图案中白色瓷砖有__________块.(用含的式子表示)
20.下面是用棋子摆成的“小屋子”.摆第1个这样的“小屋子”需要5枚棋子,摆第2个这样的“小屋子”需要11枚棋子,摆第n个这样的“小屋子”需要___________枚棋子.
三、解答题(每小题8分,共40分)
21.用字母表示图中阴影部分的面积.
22.观察下列等式:
第1个等式:.
第2个等式:.
第3个等式:.
……
按照以上规律,解决下列问题:
(1)请直接写出第4个等式:.
(2)写出你猜想的第n个等式(用含n的等式表示),并说明理由.
23.观察下列等式并回答问题:
;;;;……;
(1)可猜想第个的等式为______________________.
(2)若字母表示自然数,将第个的等式写出来,并验证其正确性.
24.用三角形和六边形按如图所示的规律拼图案.
(1)第5个图案中,三角形有________个,六边形有________个;
(2)第(为正整数)个图案中,三角形与六边形各有多少个?
(3)第2021个图案中,有多少个三角形?
(4)是否存在某个符合上述规律的图案,其中有100个三角形和40个六边形?如果存在,指出是第几个图案;如果不存在,请说明理由.
25.某种窗户由上下两部分组成,其上部是用木条围成的半圆形,且半圆形内部由三根等长的木条分隔,下部是用木条围成的边长相等的四个小正方形,木条的宽度和厚度不计.已知下部每个小正方形的边长为a米.
(1)用含a的代数式分别表示窗户的面积和所用木条的总长度;
(2)若米,窗户上安装的是玻璃,玻璃25元/平方米,木条20元/米,求制作这个窗户需要的总钱数(值取3,计算结果精确到个位).
参考答案
1.B 2.D 3.D 4.A 5.D 6.B 7.A 8.B 9.D 10.D
11.宽 12. 13. 14. 15.
16. 17. 18.1024650 19. 20.
21.【详解】解:(1)阴影部分的面积=ab﹣bx;
(2)阴影部分的面积=R2πR2.
22.【详解】(1)解:∵第1个等式为,
第2个等式为,
第3个等式为,
∴第4个等式为,
故答案为:;
(2)解:第n个等式为,
∵第1个等式为,
第2个等式为,
第3个等式为,
第4个等式为,
……,
∴第n个等式为.
23.【详解】(1)解:∵第个式子,第个式子,第个式子,第个式子,……,
∴第个式子为,
∴第个式子为,
故答案为;
(2)解:∵第个式子,第个式子,第个式子,第个式子,……,
∴第个式子为,理由如下:
∵,,
∴,
∴左边右边,
∴等式成立,
∴第个式子为.
24.【详解】(1)第1个图案中,三角形个,六边形有1个,
第2个图案中,三角形个,六边形有2个,
第3个图案中,三角形个,六边形有3个,
第4个图案中,三角形个,六边形有4个,
所以第5个图案中,三角形个,六边形有5个,
故答案为:12,5;
(2)由(1)可得,第n个图案中有三角形个,六边形有n个;
(3)第2021个图案中,
三角形有:(个);
(4)不存在,因为当时,而,
所以不存在某个符合上述规律的图案,其中有100个三形与40个六边形.
25.【详解】(1)S=2a×2aπa2=4a2πa2
即窗户的面积为(4a2πa2)米2.
15a+πa=(15+π)a(米)
即制作这种窗户所需材料的总长度(15+π)a(米).
(2)a=1时,25(4a2πa2)+20(15+π)a
≈25×(4×13×1)+20×(15+3)×1
=137.5+360
=497.5
≈498(元),即制作这扇窗户需要498元.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
