2023-2024学年人教版数学八年级上册11.1 与三角形有关的线段(课时2)同步练习(含解析)
文档属性
| 名称 | 2023-2024学年人教版数学八年级上册11.1 与三角形有关的线段(课时2)同步练习(含解析) | 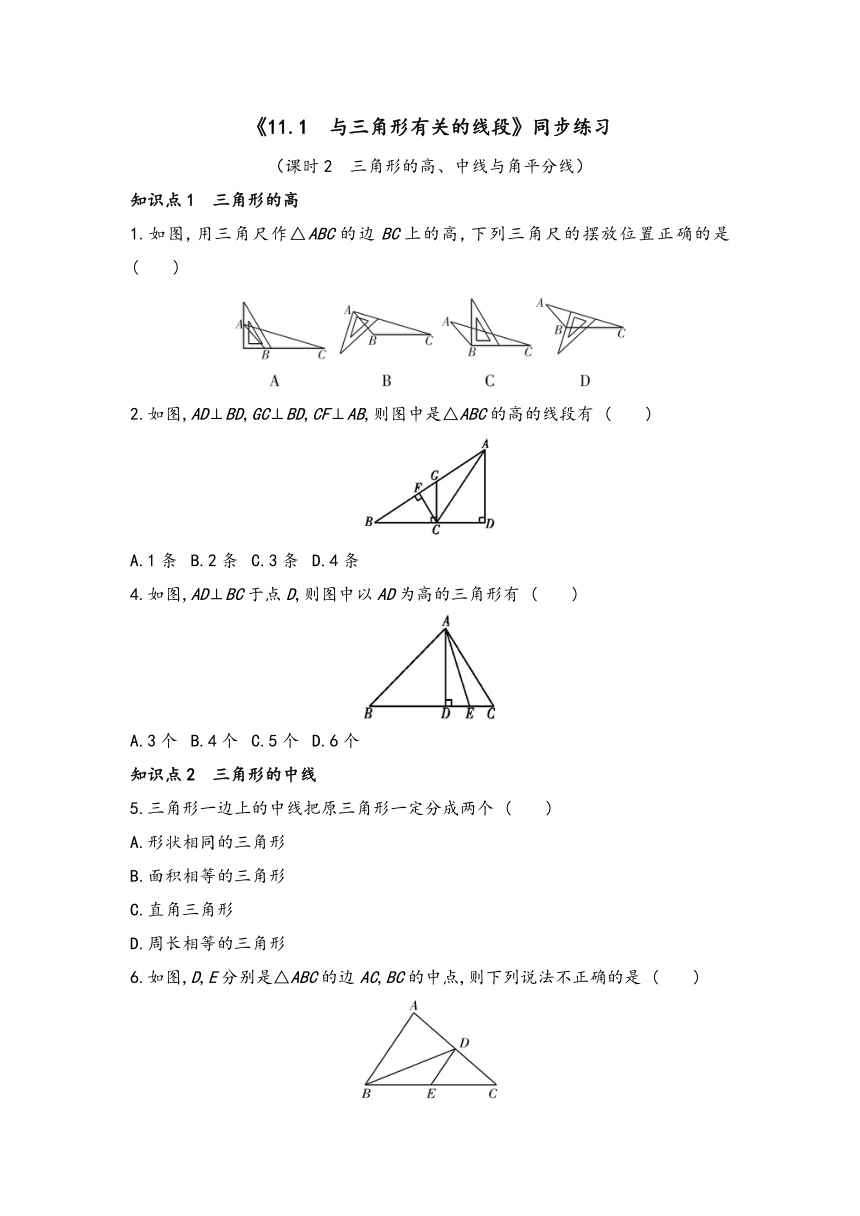 | |
| 格式 | docx | ||
| 文件大小 | 156.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-25 13:43:14 | ||
图片预览


文档简介
《11.1 与三角形有关的线段》同步练习
(课时2 三角形的高、中线与角平分线)
知识点1 三角形的高
1.如图,用三角尺作△ABC的边BC上的高,下列三角尺的摆放位置正确的是 ( )
2.如图,AD⊥BD,GC⊥BD,CF⊥AB,则图中是△ABC的高的线段有 ( )
A.1条 B.2条 C.3条 D.4条
4.如图,AD⊥BC于点D,则图中以AD为高的三角形有 ( )
A.3个 B.4个 C.5个 D.6个
知识点2 三角形的中线
5.三角形一边上的中线把原三角形一定分成两个 ( )
A.形状相同的三角形
B.面积相等的三角形
C.直角三角形
D.周长相等的三角形
6.如图,D,E分别是△ABC的边AC,BC的中点,则下列说法不正确的是 ( )
A.DE是△ABC的中线
B.BD是△ABC的中线
C.AD=DC,BE=EC
D.DE是△BCD的中线
7.如图,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形卡片的 ( )
A.三条高的交点
B.三条角平分线的交点
C.任意一点
D.三条中线的交点
8.如图,已知AD为△ABC的中线,AB=12,AC=9,△ACD的周长为27,则△ABD的周长为 .
9.如图,已知AM,AN分别是△ABC的高和中线,AB=5,AC=12,BC=13,∠BAC=90°.试求:
(1)AM的长;
(2)△ABN的面积;
(3)△ACN和△ABN的周长差.
知识点3 三角形的角平分线
10.如图,∠1=∠2,∠3=∠4,下列结论错误的是 ( )
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
C.∠3=∠ACB
D.CE是△ABC的角平分线
11.如图,在△ABC中,∠1=∠2,G为AD的中点,BG的延长线交AC于点E,F为AB上的一点,CF⊥AD于点H,则下列说法正确的有 ( )
①CH是△ACD的边AD上的高;
②AH是△ACF的角平分线和高.
③AD是△ABE的角平分线;
④BE是△ABD的边AD上的中线;
A.1个 B.2个 C.3个 D.4个
12.如图,已知AE平分∠BAC,且∠1=∠2=∠4=15°,计算∠3的度数,并说明AE是△DAF的角平分线.
参考答案
1.A
2.B 【解析】 AD是△ABC的边BC上的高,CF是△ABC的边AB上的高,所以题图中是△ABC的高的线段有2条.故选B.
3.C
4.D 【解析】 以AD为高的三角形有△ABC,△ABE,△ACD,△ABD,△AED,△ACE,共6个.故选D.
5.B 【解析】 因为三角形一边上的中线把原三角形分成了两个等底同高的三角形,所以这两个三角形的面积相等.故选B.
6.A 【解析】 ∵D,E分别是△ABC的边AC,BC的中点,∴AD=DC,BE=EC,BD是△ABC的中线,DE是△BCD的中线.故选A.
7.D 【解析】 易知支撑点是三角形卡片的重心,三角形的重心是三角形三条中线的交点,所以该点为三角形卡片的三条中线的交点.故选D.
8.30 【解析】 ∵△ACD的周长为27,∴AC+CD+AD=27.∵AC=9,∴AD+CD=18.∵AD为△ABC的中线,∴BD=CD, ∴AD+BD=18.∵AB=12,∴△ABD的周长为AB+AD+BD=30.
9.【解析】 (1)∵∠BAC=90°,AM是边BC上的高,
∴AB×AC=BC×AM.
∵AB=5,AC=12,BC=13,∴AM=.
(2)∵∠BAC=90°,AB=5,AC=12,∴S△ABC=AB×AC=30.
∵AN是边BC上的中线,∴S△ABN=S△ABC=15.
(3)∵AN为BC边上的中线,∴BN=CN,
∴△ACN的周长-△ABN的周长=AC+AN+CN-(AB+BN+AN)=AC-AB=12-5=7,
即△ACN和△ABN的周长差是7.
10.D
11.B
12.【解析】 因为AE平分∠BAC,所以∠BAE=∠CAE.
因为∠1=∠2=15°,所以∠BAE=∠1+∠2=15°+15°=30°,
所以∠CAE=∠BAE=30°,即∠4+∠3=30°,
又∠4=15°,所以∠3=15°,
所以∠2=∠3=15°,所以AE是△DAF的角平分线.
(课时2 三角形的高、中线与角平分线)
知识点1 三角形的高
1.如图,用三角尺作△ABC的边BC上的高,下列三角尺的摆放位置正确的是 ( )
2.如图,AD⊥BD,GC⊥BD,CF⊥AB,则图中是△ABC的高的线段有 ( )
A.1条 B.2条 C.3条 D.4条
4.如图,AD⊥BC于点D,则图中以AD为高的三角形有 ( )
A.3个 B.4个 C.5个 D.6个
知识点2 三角形的中线
5.三角形一边上的中线把原三角形一定分成两个 ( )
A.形状相同的三角形
B.面积相等的三角形
C.直角三角形
D.周长相等的三角形
6.如图,D,E分别是△ABC的边AC,BC的中点,则下列说法不正确的是 ( )
A.DE是△ABC的中线
B.BD是△ABC的中线
C.AD=DC,BE=EC
D.DE是△BCD的中线
7.如图,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形卡片的 ( )
A.三条高的交点
B.三条角平分线的交点
C.任意一点
D.三条中线的交点
8.如图,已知AD为△ABC的中线,AB=12,AC=9,△ACD的周长为27,则△ABD的周长为 .
9.如图,已知AM,AN分别是△ABC的高和中线,AB=5,AC=12,BC=13,∠BAC=90°.试求:
(1)AM的长;
(2)△ABN的面积;
(3)△ACN和△ABN的周长差.
知识点3 三角形的角平分线
10.如图,∠1=∠2,∠3=∠4,下列结论错误的是 ( )
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
C.∠3=∠ACB
D.CE是△ABC的角平分线
11.如图,在△ABC中,∠1=∠2,G为AD的中点,BG的延长线交AC于点E,F为AB上的一点,CF⊥AD于点H,则下列说法正确的有 ( )
①CH是△ACD的边AD上的高;
②AH是△ACF的角平分线和高.
③AD是△ABE的角平分线;
④BE是△ABD的边AD上的中线;
A.1个 B.2个 C.3个 D.4个
12.如图,已知AE平分∠BAC,且∠1=∠2=∠4=15°,计算∠3的度数,并说明AE是△DAF的角平分线.
参考答案
1.A
2.B 【解析】 AD是△ABC的边BC上的高,CF是△ABC的边AB上的高,所以题图中是△ABC的高的线段有2条.故选B.
3.C
4.D 【解析】 以AD为高的三角形有△ABC,△ABE,△ACD,△ABD,△AED,△ACE,共6个.故选D.
5.B 【解析】 因为三角形一边上的中线把原三角形分成了两个等底同高的三角形,所以这两个三角形的面积相等.故选B.
6.A 【解析】 ∵D,E分别是△ABC的边AC,BC的中点,∴AD=DC,BE=EC,BD是△ABC的中线,DE是△BCD的中线.故选A.
7.D 【解析】 易知支撑点是三角形卡片的重心,三角形的重心是三角形三条中线的交点,所以该点为三角形卡片的三条中线的交点.故选D.
8.30 【解析】 ∵△ACD的周长为27,∴AC+CD+AD=27.∵AC=9,∴AD+CD=18.∵AD为△ABC的中线,∴BD=CD, ∴AD+BD=18.∵AB=12,∴△ABD的周长为AB+AD+BD=30.
9.【解析】 (1)∵∠BAC=90°,AM是边BC上的高,
∴AB×AC=BC×AM.
∵AB=5,AC=12,BC=13,∴AM=.
(2)∵∠BAC=90°,AB=5,AC=12,∴S△ABC=AB×AC=30.
∵AN是边BC上的中线,∴S△ABN=S△ABC=15.
(3)∵AN为BC边上的中线,∴BN=CN,
∴△ACN的周长-△ABN的周长=AC+AN+CN-(AB+BN+AN)=AC-AB=12-5=7,
即△ACN和△ABN的周长差是7.
10.D
11.B
12.【解析】 因为AE平分∠BAC,所以∠BAE=∠CAE.
因为∠1=∠2=15°,所以∠BAE=∠1+∠2=15°+15°=30°,
所以∠CAE=∠BAE=30°,即∠4+∠3=30°,
又∠4=15°,所以∠3=15°,
所以∠2=∠3=15°,所以AE是△DAF的角平分线.
